自动驾驶汽车轨迹规划方法综述

吕贵林 高洪伟 陈涛 田鹤 韩爽

（中国第一汽车股份有限公司研发总院，长春 130013）

0 引言

随着多家公司相继提出约在2025 年实现L5 级自动驾驶，真正意义上的自动驾驶车辆离我们越来越近。

自动驾驶汽车的最早贡献之一可以追溯到20世纪20 年代的Houdina 无线电控制公司，该公司成功地演示了一辆由尾随车辆发送的无线电信号控制的汽车。

当今，自动驾驶汽车的研究进入了蓬勃发展时期，许多自动驾驶汽车的相关技术已经被应用到高级驾驶辅助系统（Advanced Driving Assistance Systems,ADAS）中，如巡航控制（Cruise Control,CC）、智能速度适应（Intelligent Speed Adaptation,ISA）、车道保持辅助（Lane Keeping Assist,LKA）和车道偏离预警（Lane Departure Warning, LDW）、变道辅助（Lane Change Assist, LCA）、自适应巡航控制（Adaptive Cruise Control,ACC）和自动紧急制动（Automatic Emergency Braking,AEB）等[1]。

自动驾驶的分层体系由3 个模块组成，包括感知（Perception）、规划（Planning）、控制（Control），如图1所示。根据实现方法不同，有些系统还具有地图、定位、预测和V2X（Vehicle to X）通信模块。通常情况下规划模块被分为3 个层次，包括全局路由规划（Routing planning）、行为决策（Behavior decision）和轨迹规划（Trajectory planning）。路由规划根据环境信息（如交通语义地图）规划一条全局路线，行为决策模块在给定的路由下根据交通规则、其他交通参与者的行为感知、道路状况和基础设施信号做出语义层动作决策（如车道保持、换道）。轨迹规划层负责生成一条适合车辆运动、带有速度信息的轨迹。这一层需要考虑安全性、效率、驾驶舒适性、不确定信息处理（如传感器精度、遮挡区域）等因素。

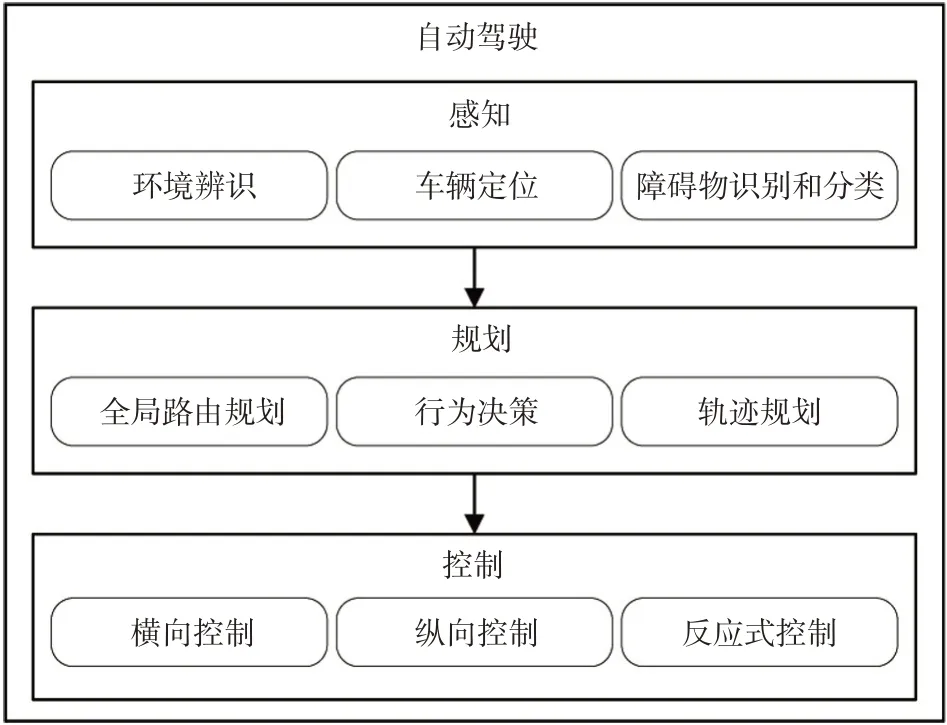
图1 自动驾驶控制体系

自动驾驶发展至今，轨迹规划一直是自动驾驶研究的重点，安全问题一直是自动驾驶考虑的首要方面，一个优秀的轨迹会大幅提高驾驶安全。

本文通过综述自动驾驶汽车轨迹规划相关文献，重点研究规划模块中轨迹规划策略。第1章，分析对比了主要的轨迹规划方法，并给出了这些方法的优缺点；在第2章，给出了已经在实际中应用的轨迹规划算法，并进行相关分析。第3章，总结出轨迹规划领域存在的问题与挑战，并分析了未来发展方向。

1 轨迹规划方法

现有的轨迹规划算法主要起源于移动机器人领域，随自动驾驶技术兴起后被应用于解决自动驾驶的轨迹规划问题。根据它们在自动驾驶领域的应用，这些轨迹规划技术被分为图搜索、采样、数学优化、插值曲线以及机器学习。下面分别对以上技术进行阐述。

1.1 图搜索

图是数据结构中非常重要的一个概念，包含了节点和边。在自动驾驶中，通常可以将地图存储为栅格地图，每一格就代表了图的节点，格与格之间的连线就代表了边。

基于图搜索的路径规划技术在表示为图的状态空间中搜索汽车当前状态和目标状态之间的最佳路径。其基本思想是穿越一个状态空间，从当前节点到达目标节点。这个状态空间通常表示为一个网格或格子，用来描述物体在环境中的位置，从规划的角度来看，路径设置可以实现访问网格中不同状态的图搜索算法，从而给出路径规划问题一个解决方案。基于图搜索的轨迹规划技术在基于图搜索的路径规划技术上进行扩展，来说明车辆状态随时间的演化。但传统图搜索的算法所得到的路径通常不能满足车辆动力学要求，或无法适用于动态环境，因此实际应用于自动驾驶时需针对这类些问题进行改进。

1.1.1 Dijkstra

Dijkstra 算法[2]由荷兰科学家Dijkstra 于1959年首先提出，是搜索最短路径的经典算法。Dijkstra算法的主要特点是以起始点为中心向外层扩展（广度优先搜索思想），直到扩展到终点为止。它的基本原则是：反复检查最近的尚未检查的节点，将其邻居添加到要检查的节点集中，并在达到目标节点时停止。Dijkstra算法步骤如Algorithm 1所示[2]。

其中，INITIALIZE 为初始化函数，其算法步骤如Algorithm 2所示[2]。

Algorithm 2:INITIALIZE for each v ∈G.V vd=∞∕∕初始时节点到起点的距离为无穷vπ=NULL ∕∕初始所有顶点的父节点为空sd=0 ∕∕起点的距离为0

RELAX为路径替换函数，其算法如Algorithm 3所示[3]。

Algorithm 3:REALAX(u,v,w)if vd ＞ud+w(u,v) then ∕∕w( )u,v 为u 到v 的权值vd=ud+w(u,v) ∕∕更新v 到起点距离vπ=u ∕∕更新v 的父节点

Algorithm 1:Dijkstra INITIALIZE(G,s)S=∅ ∕∕S 开始为空集，用来存储已访问的顶点Q=G.V ∕∕初始化最小优先队列Q，存放图G 的所有节点while Q ≠∅ do u= dequeue-min(Q)∕∕Q 中最小元素出队if u 为目标节点then break else S=S ∪{u}for each v ∈G.adj[u] and v is not in S RELAX(u,v,w)

最终所需的最短路径通过从目标节点不断搜寻父节点得到的顶点集合得到。

Victor Tango[3]团队在2007 年的DARPA 挑战赛上用Dijkstra 算法为Odin 生成路径。2013 年，Kala 和Warwick 使用Dijkstra 生成路径[4]，仅在计算机模拟中进行了测试。

Dijkstra算法的成功率是最高的，因为它每次必能搜索到最优路径。但Dijkstra 算法的搜索速度是最慢的，随着图维度的增大，其计算效率会明显变低。其时间复杂度为O(n2)，其中n代表算法的数据规模，在图搜索算法中代表空间的节点个数，即执行时间和节点的个数相关。因此，在地图数据较大时很难满足路径规划中实时性的要求。

1.1.2 A∗算法

A*算法[5]的主要特点是在Dijkstra 算法的基础上为空间的每个节点定义了一个启发函数（估价函数）h(v)，启发函数为当前节点v到目标节点的估计值。在A*算法中遍历节点的优先级通过以下公式计算：

式中，f(v)是节点v的综合优先级；g(v)为节点v距离起点的代价；h(v)为节点v距离终点的预计代价。

当h(v)始终为0时，算法通过g(v)控制优先级，此时算法就变回Dijkstra 算法。A*算法[5]的步骤如Algorithm 4所示。

Algorithm 4:A*S=∅ Q=∅Q ⇐s while Q ≠∅ do u= dequeue-min(Q)∕∕取出Q 中f 值最小的节点if u 为目标节点then break else S=S ∪{u}for each v ∈G.adj[u]计算f(v)if v is in Q then if v 当前估价值f(v)小于Q 中的f(v) then Update Q ∕∕替换Q 中f(v)else if v is in S then if v 当前估价值f(v)小于S 中的f(v) then Update S ∕∕替换S 中f(v)Q ⇐v else if v is not in S and is not in Q then Q ⇐v

启发函数相当于为搜索提供了一个方向，可以减少搜索节点的数量从而提高效率。

A*算法为全局规划算法，因此常用于路径规划。Leedy 等[6]在2005 年DARPA 大挑战赛中采用A*算法为自动驾驶汽车构建路径。Ziegler等[7]在2008年提出了一种将A*与2 种不同启发式代价函数旋转平移旋转（Rotation Translation Rotation, RTR）和Voronoj 图结合的路径规划方法。

在轨迹规划中Fassbender 等[8]提出了2 种新颖的A*节点扩展方案，分别是一次性扩张（One-Shot Expansions）和纯跟踪扩张（Pure-Pursuit Expansions）。一次性扩张通过一步(或一次)找到可行的轨迹，将车辆从当前节点带到目标，能够有效改善常规的A*扩展缓慢的情况。

纯跟踪扩张使用纯追踪控制器生成短边，引导汽车沿着全局参考路径行驶。常规A*中对控制输入离散化的需求可能导致路径不平滑，从某种意义上说，它们包含非自然转向，这使得它很难精确地遵循光滑的参考路径。一种解决办法是首先使用A*和有限数量的运动基元规划一个粗路径，然后使用数值优化对路径进行平滑。这种方法的问题是，在需要高度精确机动的场景中，它可能会失败，因为第一步的粗离散可能会阻止规划算法找到任何解决方案。因此，Fassbender 等[8]将纯跟踪与A*结合开发了纯追踪扩张法，一种生成轨迹的替代方法，这种方法可以平滑地沿着道路行进。

A*算法在当前自动驾驶领域的应用也十分广泛，2021年Pérez-Gill等[9]基于CARLA和ROS联合仿真提出了一个适用于车辆的深度强化学习框架，利用A*算法获得节点，来生成全局路径。

A*算法在静态道路网络中非常有效，但不适于在动态道路网络，即权重不断变化的动态环境下，例如出现塌方、车祸、阻塞等状况。

1.1.3 D*算法

通常，每次使用感知数据更新世界模型时，都要重复寻找从车辆当前位置到目标区域的最短路径。由于每次更新通常只影响到图的一小部分，所以每次完全从头开始搜索是浪费时间。针对这个问题在A*的基础上设计出实时重规划搜索算法D*[10]。D*也被称为动态A*（Dynamic A-Star,D-Star），该算法能够在未知的、部分已知的、变化的环境中高效、最优、完整地规划路径。与A*不同的是D*以目标节点开始进行搜索，当路径上遇到障碍物时所受到影响的点会增加成本，从而在循环时避免进行全面搜索，并且D*算法存储了每个节点到目标结点的最短路径信息，故在重新规划时效率大大提升，如Algorithm 5所示[10]。

Algorithm 5:D*S=∅ Q=∅Q ⇐target while Q ≠∅ do u= dequeue-min(Q)∕∕取出Q 中k 值最小的节点，k 为所有变化h 值中最小的值if u 为目标节点then break else S=S ∪{u}for each v ∈G.adi[u]h(v)=h(u)+w(u,v) ∕∕h(v)为目标节点到v 点的实际值if v is in Q then if v 当前估价值h(v)小于Q 中的h(v) then Update Q ∕∕用当前估价值h(v)替换Q 中原本h(v)，并将k 值取最小的h 值elseif v is in S then if v 当前估价值h(v)小于S 中的h(v) then Update S ∕∕替换s 中的h(v)，k 取最小的h值Q ⇐v elseif v is not in S and is not in Q then Q ⇐v

在D*基础之上Focussed D*[11]和D*Lite[12]也被设计用来在每次环境底层发生变化时高效地重新计算最短路径，同时保留以前搜索结果中的信息。

1.1.4 状态栅格算法

状态栅格（State Lattice）[13]是一个搜索图，传统的A*算法用于寻找最短路径，但最终得到的图对车辆来说未必可行，因此需要在图的节点之间建立可行路径，如图2，其中顶点表示状态，边表示连接满足机器人运动学约束状态的路径。顶点以一种常规的方式放置，这样即使经过严格的平移和旋转，也可以使用相同的路径来构建从每个顶点到目标的可行路径。这样，到达目标的轨迹很可能被表示为图2中的边序列。状态格能够处理多个维度，例如位置、速度和加速度，并且适用于动态环境。然而，其计算成本很高，因为该算法评估了图中的每一个可能的解决方案[1]。

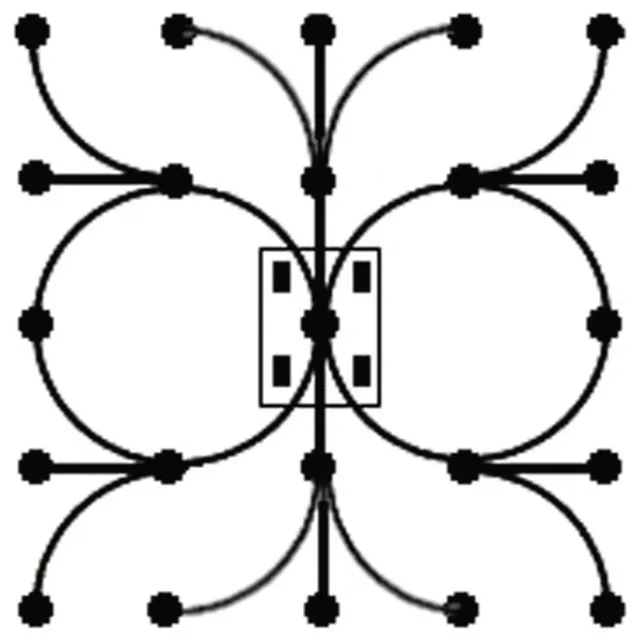
图2 状态栅格示意[13]

McNaughton等[14]提出了一种用于轨迹规划的时空联合状态栅格（Conformal spatiotemporal state lattice）。该算法围绕着一条中心线路径构造状态格，定义了道路上从中心线横向偏移的节点，并使用一种优化算法计算节点之间的边缘。这个优化算法找到一个多项式函数参数，该函数定义了任意对连接的节点边。为每个节点分配一个状态向量，该状态向量包含一个姿态、加速度剖面，以及时间和速度范围。与追求时间和速度间隔更精细的离散化相比，加速度剖面以更少的成本增加了轨迹多样性。此外，时间和速度的范围通过将时间和速度分配到图搜索阶段，而不是图构建阶段，降低了计算成本。Xu等[15]提出了一种迭代优化方法，将其应用于时空联合状态栅格轨迹规划，减少了规划时间，提高了轨迹质量。Li等[16]通过使用三次多项式曲线生成候选路径来构建状态栅格。速度剖面也被用来计算分配所生成路径的姿态，得到的轨迹由一个代价函数来评估，并选择最优的一个。表1为图搜索规划算法对比。

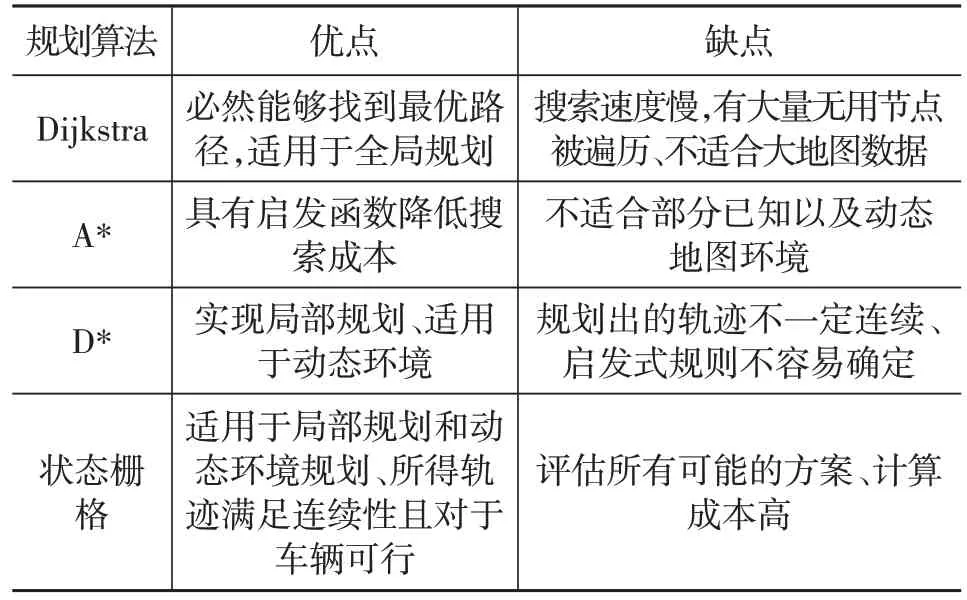
表1 图搜索规划算法对比

1.2 采样

在基于图搜索的轨迹规划中大部分需要通过网格化来达到离散化的目的，而基于采样的技术对状态空间进行抽样以达到离散化的目的，从而寻找汽车当前状态和下一个目标状态之间的联系[17]。

1.2.1 RRT

轨迹生成的快速遍历随机树（Rapidly exploring Random Trees,RRT）方法[18]使用状态空间中的随机样本，从汽车当前状态逐步构建搜索树，通过随机采样增加叶子节点，生成一个随机拓展树，当扩展的随机叶子节点进入目标区域，就得出了一条从起始位置到目标位置的路径，如Algorithm 6所示。

Algorithm 6:RRT Initialize RRT-tree ∕∕初始化RRT搜索树RRT-tree ⇐xstart while()xrandom = Smple( M)∕∕在地图M 中随机采样获得xrandom 节点xnear =Near(xrandom,RRT-tree)∕∕在搜索树中找到距离xrandom 最近的节点if distance( xrandom, xnear) ＞ th re sh old then ∕∕如果xrandom 与xnear 距离大于阈值xnew =Steer(xrandom, xnear, th re sh old)∕∕xnew 为xnear与xrandom 沿线上一点，与xnear 距离为th re sh old else xnew= xrandom if nocollision( M, edge( xnew, xnear)) then ∕∕如果xnew与xnear 连线没有穿过地图障碍物RRT-tree ⇐xnew RRT-tree ⇐edge(xnew, xnear)if distance(xnew, xtarget)＜th re sh old then break

与人类驾驶汽车一样，自动驾驶汽车也受到一系列规则约束，然而在某些情况下（例如在道路上超车事故车辆）这些约束需要打破，此时就可能出现违反交通规则的问题。如果将交通规则以代价函数的形式与自动驾驶结合，则可以使用传统的运动规划方法来寻找代价最小的路径。

基于RRT，RRT-Connect[19]能够更快速地找到可行路径，RRT-Connect同时扩展2棵树，一棵树从起始点扩展，另一棵树从目标点扩展，当2棵树之间建立联系时，规划器停止搜索。

然而由于树的扩展方向是随机的，使得最终得到的路径不平滑、不符合车辆动力学且并不是最短路径。并且，虽然通过随机的方式能够提升搜索树扩展的速度，但可能扩展大量无用节点，占用大量内存。

为了解决RRT 所得轨迹不满足车辆动力学的问题，Kuwata 等开发了闭环RRT（Closed Loop RRT,CLRRT）算法[20]。在CL-RRT 算法中，将闭环控制器与RRT 结合使用。树中的每个节点都是通过使用带有闭环动力学的低层控制器来扩展的，这样树中的每条边都是动态可行的。在CL-RRT 中，参考命令r被输入到控制器。该控制器向车辆动力学模型输入车辆控制命令u，如图3所示，该闭环系统生成动态可行轨迹x。因此，闭环控制器影响对动态可行轨迹的采样，而不是直接从配置空间采样。

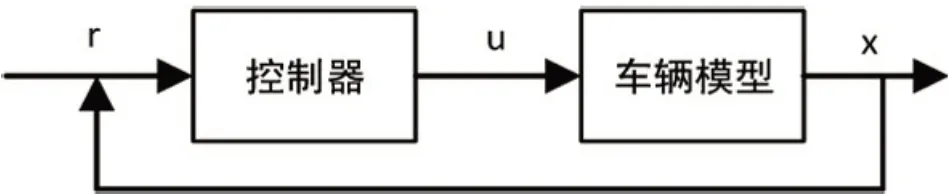
图3 CL-RRT车辆控制模块

2.2.2 RRT*

传统RRT算法不能保证所得路径是最优的，为此Karaman等[21]开发了一个必然会收敛到最优解的算法RRT*。RRT*算法在每次迭代后都会在局部更新搜索树，以优化路径。相较于传统RRT 算法多了2 个过程，分别为重新为加入搜索树的有效节点选择代价更小的父节点，即re-choose，以及重布线随机树，即rewire，如Algorithm 7所示。

Algorithm 7:RRT*Initialize RRT-tree RRT-tree ⇐xstart while()xrandom =Smple(M)xnear =Near(xrandom,RRT-tree)if distance(xrandom, xnear)＞th re sh old then xnew =Steer(xrandom, xnear, th re sh old)else xnew= xrandom if nocollision(M,edge(xnew, xnear))then RRT-tree ⇐xnew xmin =re-choose( xnew,RRT-tree)∕∕在树中找到一个代价最小的节点作为xnew 新的父节点RRT-tree ⇐edge(xmin, xnew)Rewire()∕∕根据新的父节点重新配置搜索树if distance(xnew, xtarget)＜th re sh old then break

RRT*算法是渐进优化的，也就是随着迭代次数进行局部搜索树的优化更新（通常会限制最大循环数），得到的路径是越来越优化的，但在有限时间内无法得到最优解，也就是说要得到较优的路径，需要耗费的时间更多。

RRT*-Connect将RRT*与RRT-Connect结合，形成了一种双向方法，可以返回一个接近最优解的方案[22]。虽然RRT*和RRT*-Connect 能够返回一个更优的路径，但这不并是一个能够有效降低计算成本的方案。Gammell 等证明了现有方法随着空间维度的扩大，有效性显著降低[23]，因此提出了Informed RRT*,在找到第一个可行方案后，根据椭圆上任意一点到其焦点的距离之和相等的特性，以起始点和目标点为椭圆焦点，用路径长度作为椭圆上一点到两焦点的距离之和画一个椭圆，算法只需要在椭圆内抽样即可，每找到一条更短的路径，椭圆的范围也会随之变小。

然而Informed RRT*同样存在其它单向树规划算法的问题，需要大量时间来找到相对优化的路径，尤其是当遇到狭窄通道时，所需的时间更多。为了应对这个问题Mashayekhi 等[24]设计出Informed RRT*-Connect，通过RRT*-Connect 来寻找路径，然后通过椭圆限制优化的范围，从而降低搜索时间。

1.2.3 PMP

在一个时间段内搜索全局图会降低效率。因此，可以使用局部运动规划（Partial Motion Planning,PMP），而不是搜索整个状态空间，以降低计算复杂度。Benenson 等[25]在使用PMP 时考虑了不可避免的碰撞状态（Inevitable Collision States,ICS），通过在局部空间采样节点进行扩展，并删除ICS 节点避免碰撞。表2为采样规划算法的优缺点对比。

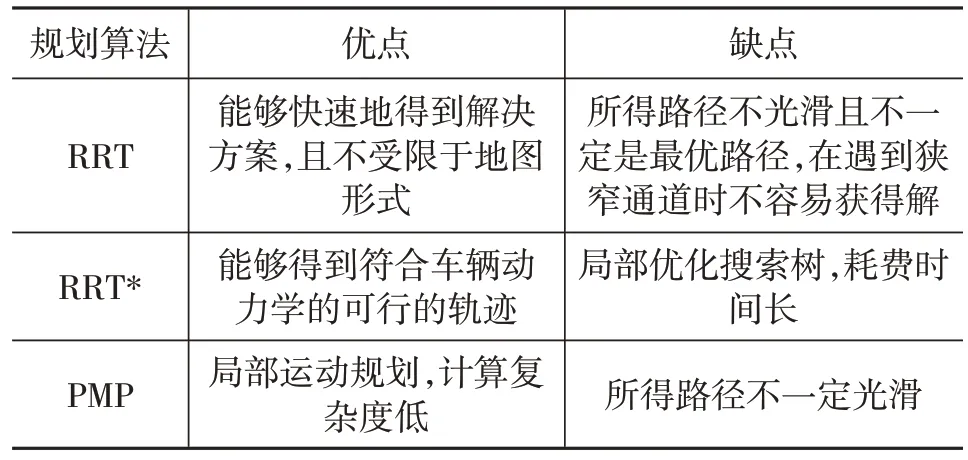
表2 采样规划算法对比

1.3 数学优化

数学优化方法的目标是最小化或最大化受不同约束变量的函数。在轨迹规划中，通常用于平滑之前计算的轨迹，也用于从运动学约束计算轨迹[26]。基于数值优化的自动驾驶汽车轨迹规划方法主要有函数优化和模型预测方法。

1.3.1 函数优化

函数优化方法通过最小化代价函数来寻找轨迹，该方法考虑了轨迹的位置、速度、加速度约束条件。这些方法能较好地考虑汽车运动学、动力学约束和环境约束。但是，函数优化方法计算成本很高，因为优化过程发生在每个运动状态，并依赖于全局路径点。Ziegler等利用函数优化方法对自动驾驶汽车Bertha进行轨迹规划[27-28]。Ziegler等通过最小化一个函数来寻找C2连续轨迹，也就是在轨迹拼接处二阶连续可导的轨迹，并且该函数考虑了车辆位置、速度、加速度作为规划参数，遵循了轨迹的约束条件。1.3.2 模型预测

模型预测通过预测未来车辆的状态，生成车辆当前状态到下一目标状态之间的控制指令[29]。使得车辆控制命令参数化，并满足状态约束，其动力学可以用微分方程表示。在2007 年的DARPA 挑战赛中，卡梅隆大学使用模型预测进行自动驾驶汽车Boss 的轨迹规划[30]。

Li 等[31]使用了一种基于状态采样的轨迹规划方案，该方案对沿着路线的目标状态进行采样。采用一种模型预测路径规划方法来生成连接汽车当前状态和采样目标状态的路径。速度剖面用来分配沿着生成路径的每个状态的速度。采用考虑安全性和舒适性的成本函数来选择最佳轨迹。

Cardoso 等[32]采用了一种模型预测方法进行自动驾驶汽车的轨迹规划。为了计算轨迹，Cardoso等使用一种优化算法来获得轨迹控制参数，以最小化到目标状态的距离、到路径的距离以及与障碍物的接近程度。表3为数学优化方法对比。

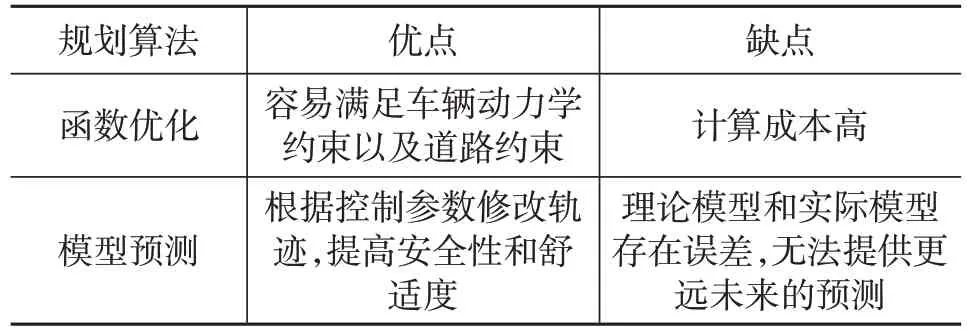
表3 数学优化规划算法对比

1.4 插值曲线

基于插值曲线（Interpolating Curve）的技术可以对已知的一组姿态(例如，路径的姿态)进行插值，并在考虑汽车运动学和动力学约束、舒适性、障碍物参数情况下，构建出更加平滑的轨迹。当遇到存在障碍的情况下，只需创造一条新的路径去克服事件，然后重新回到之前计划的路径中[1]。

1.4.1 圆弧与直线

1990年，为了找到满足车辆动力学的平滑最短路径，Reeds等[33]设计了圆弧与直线（Lines and Circles）算法。Lines and Circles 是解决类车车辆规划问题的一种简单的数学方法，针对不同路段的路网可以用直线和圆形的路径点插值来表示。

1.4.2 回旋曲线

回旋曲线（Clothoid Curves）允许定义具有线性可变曲率的轨迹，这样在直线到曲线段之间的过渡是平滑的。回旋曲线与其它轨迹规划方法相比的主要优势在于它的曲率是线性变化的，它可以防止向心加速度的突然变化，从而提高车辆的驾驶舒适性，对于载人或重型的货物运输是非常重要的[34]。然而，由于定义该曲线的积分和它所依赖的全局路径点，使得该曲线具有较高的计算成本。Alia 等[35]使用回旋约束（Clothoid Tentacles）进行轨迹规划。根据不同的速度和不同的初始转向角度，从汽车的重心开始，以线圈的形式计算触须。使用路径跟踪控制器，从触须的几何参数中获取转向角度命令，并在占用网格地图上运行碰撞检查，将触须划分为可行驶或不可行驶。在可行驶触须中，根据几个标准选出最佳触须。Mouhagir等也使用回旋触须进行轨迹规划[36-37]。然而，他们使用了一种受马尔可夫决策过程（Markov Decision Process,MDP）启发的方法来选择最好约束。

2.4.3 多项式曲线

多项式曲线（Polynomial Curves）常被用于满足插值点所需的约束条件，基于多项式的规划允许独立计算横向和纵向车辆运动，同时保证轨迹具有连续的速度、加速度和曲率，可避免圆弧与直线中曲率不连续的问题。

Benloucif 等[38]提出一种计划轨迹规划方法，这是一种能够根据驾驶员的行动和意图不断调整的自动化共享驾驶控制框架。Benloucif 等利用多项式，结合机动决策、冲突管理和驾驶员监控信息，制定协同轨迹规划。

1.4.4 样条曲线

样条曲线（Spline Curves）是一种分段多项式参数曲线。它被划分为子区间，可以理解为多段、多项式曲线的拼接，这种拼接必须满足平滑衔接，可以被定义为多项式曲线。每个子段之间的连接称为结点(或控制点)，这些结点通常具有高度平滑的约束。这种曲线计算成本低，因为它的行为是由节点定义的。然而，它的结果可能不是最优的，因为它更关注于实现子区间之间的连续性，而不是满足道路约束。

Chu[39]和Hu[40]等使用3 次样条曲线进行路径规划。2人的方法都是从道路网络中提取的路线构造一条中心线。它们使用弧长和到中心线的偏移生成一系列参数化3次样条曲线来代表可能的候选路径，根据考虑安全性和舒适性的函数选择最佳路径。表4为插值曲线规划算法对比。

表4 插值曲线规划算法对比

1.5 机器学习

将机器学习应用于自动驾驶汽车领域，可以以模块化的形式，将机器学习方法与自动驾驶其它模块经典算法融合（例如基于深度学习的目标检测器为经典的A*路径规划算法提供输入），或将感官信息直接映射到车辆控制命令，使开发“端到端”解决方案成为可能，所谓“端到端”即使系统可以像人类驾驶员一样驾驶车辆，即输入是目的地、关于路网的知识和各种传感器信息，输出是直接的车辆控制命令，如转向、制动[41-42]。

卷积神经网络（Convolutional Neural Networks,CNN）是图像识别领域最成功的深度学习模型，已经在自动驾驶车道和车辆检测中得到了广泛[43]。

在DARPA城市挑战赛中，用于不同驾驶场景的行为决策方法有启发式组合[30]、决策树[44]和有限状态机（Finite State Machine，FSM）[45]。然而，在现实世界中驾驶汽车，即使完全了解当前的交通状态，但周围交通参与者的意图是未知的。因此需要对其它车辆、自行车和行人未来轨迹的意图预测和估计。目前主流方案有基于机器学习的技术，如高斯混合模型[46]、高斯过程回归[47]或基于支持向量机和人工神经网络的预测[48]。而对于自动驾驶决策方法可分为基于规则的决策方法，基于马尔可夫理论的决策方法以及基于人工智能（主要是循环神经网络）的决策方法3类[49]。

而在轨迹规划中有2种最具代表性的深度学习模式，分别为基于模仿学习（Imitation Learning,IL）的规划和基于深度强化学习（Deep Reinforcement Learning,DRL）的规划。

基于模仿学习的规划通过记录驾驶经验来学习人类驾驶员的行为，该策略包含了一个从人的示范开始的车辆教学过程[50-51]。基于DRL的轨迹规划主要是在模拟器中学习驾驶轨迹规划[52-53]。

在轨迹规划中IL 和DRL 各有优缺点。IL 的优势在于它可以用从真实世界收集的数据进行训练。尽管如此，这些数据在不常遇到的交通状况下（例如，驾驶偏离车道，交通事故等）是稀缺的，因此当面对没能覆盖到的数据时，网络的反应是不确定的。另一方面，尽管DRL系统能够在模拟世界中探索不同的驾驶情况，但当这些模型移植到现实世界中时，往往会与模拟世界得到的结果有偏差。表5为机器学习规划算法对比。

表5 机器学习规划算法对比

2 轨迹规划方法应用

本章列举了至今为止关键性的自动驾驶项目，并对这些项目中实际采用的轨迹规划方法进行分析。

为了推动自动驾驶技术的发展，美国国防高级研究计划局（Defense Advanced Research Projects Agency，DARPA）在过去十几年里组织了3场“DARPA挑战赛”。

第一次挑战赛（DARPA Grand Challenge）于2004年在美国莫哈韦沙漠举行，要求自动驾驶汽车在10 h内穿越229 km 的沙漠路线。所有参加比赛的汽车都在前几英里失败了，卡内基梅隆大学的汽车Sandstorm走了最远的距离，完成了11.78 km 的路程，可惜在一个急转弯后被挂在了一块岩石上。这一次比赛也让参赛者发现了自身在环境信息采集、动态环境规划以及局部避障上的不足。

2005 年DARPA 挑战赛[54]中，共有23 名车队进入决赛，4 辆车在规定时间内完成了比赛。其中斯坦福大学的汽车Stanley[45]获得了第1 名。在比赛前DARPA 向所有参赛者提供了路由定义数据格式（Route Definition Data Format,RDDF）文件，RDDF文件在一定程度上消除了全局路径规划的需要，因此参赛者需要着重解决局部的避障问题。Stanley 的路径规划并不是在全局坐标系下进行，而是使用相对坐标系，通过相对RDDF 基础路径的横向偏移实现避障。然而这一前提是保证基础路径平滑可行。RDDF提供的路径只是粗略的描述，并不保证可行，于是Stanley 通过最小二乘法优化调整RDDF 的所有坐标点，再通过3 次样条插值得到可微路径。当无障碍时，Stanley的行驶轨迹与基本路径平行，当遇到障碍时Stanley计划一个平滑的横向偏移。这种先计算相对中心线偏移，然后通过数学优化的方法可以使生成的轨迹更加平滑，但是对原始轨迹的要求较高。在原始轨迹不可行的情况下，可能出现无解情况。

2007年，DARPA 城市挑战赛[55]举行。6辆车在规定时间内完成了比赛，卡内基梅隆大学的汽车Boss[30]获得了第1名，Boss采用模型预测方法进行轨迹规划，它生成从中心线路径导出的一系列目标状态的轨迹。为了计算每个轨迹，他们使用一种数学优化算法，该算法逐渐修改轨迹控制参数的初始近似值，直到轨迹终点误差在可接受的范围内。轨迹控制参数是定义曲率轮廓样条曲线的轨迹长度和3个结点。基于多个因素，包括当前道路速度极限、最大可行速度和目标状态速度，生成每个轨迹的速度剖面。根据其与障碍物的距离、到中心线的距离、平滑度、终点误差和速度误差来选择最佳轨迹。虽然这种基于模型预测的方法可以设计多种约束条件，使生成的轨迹更适合车辆运动，但是该方法的计算量较大，在实时性要求较高的场景下可能会出现控制滞后的情况。第2名是斯坦福大学的汽车Junior[56]，它使用了一种混合A*算法（Hybrid A*），混合A*在常规A*的每个特定单元上分配了一个连续坐标，以此解决了A*所得的离散路径无法应用于现实世界的问题。弗吉尼亚理工大学的汽车Odin[3]获得了第3 名，其轨迹规划首先使用车道和障碍物数据创建成本网格图，然后选择一系列动作达到目标状态，最后将这一系列动作处理成可行的运动轮廓。混合A*天然考虑了车辆运动学约束，通过合理的设计启发函数，可以获得一条满足终点航向约束的最短路径，但是该方法没有考虑车辆的速度配比，需要单独对速度进行规划。

此次比赛证明了城市环境中的自动驾驶是可行的。尽管日常交通的复杂程度要高于比赛中的挑战，但DARPA仍被誉为自动驾驶汽车发展的里程碑。从该次比赛中可以看出，在实际项目中，大部分轨迹规划方法采用了基于搜索、数学优化和混合A*算法。虽然DARPA 距今已过了十多年，但基于搜索、采样、插值经典算法的轨迹规划在如今的自动驾驶开发项目中仍有着广泛的应用。

百度Apollo自动驾驶框架于2018年首次开源，该项目不断迭代更新日渐成熟，并逐渐成为国内外自动驾驶研究的样板。该项目轨迹规划算法在Frenet 坐标系中使用动态规划和二次规划方法进行路径规划和速度规划，因此这是一种路径和速度解耦的方法，该算法被称为EMplanner。该框架在其3.5 版本中首次采用了基于场景的规划方法，使得算法在不同场景中的适应性和规划效果得到提升。然而其对场景的确定和分类采用基于规则的方法，在传感器失真和部分可观测的情况下可能导致对场景的错误判断。未来可以通过应用机器学习方法对这一部分的内容进行改进，从而进一步提高规划算法鲁棒性。该框架的后续版本中使用了端到端机器学习方法进行规划，在其给出的仿真对比效果中可以明显看到机器学习方法的效果显著高于传统规划方法。表6为轨迹规划5种方法对比。

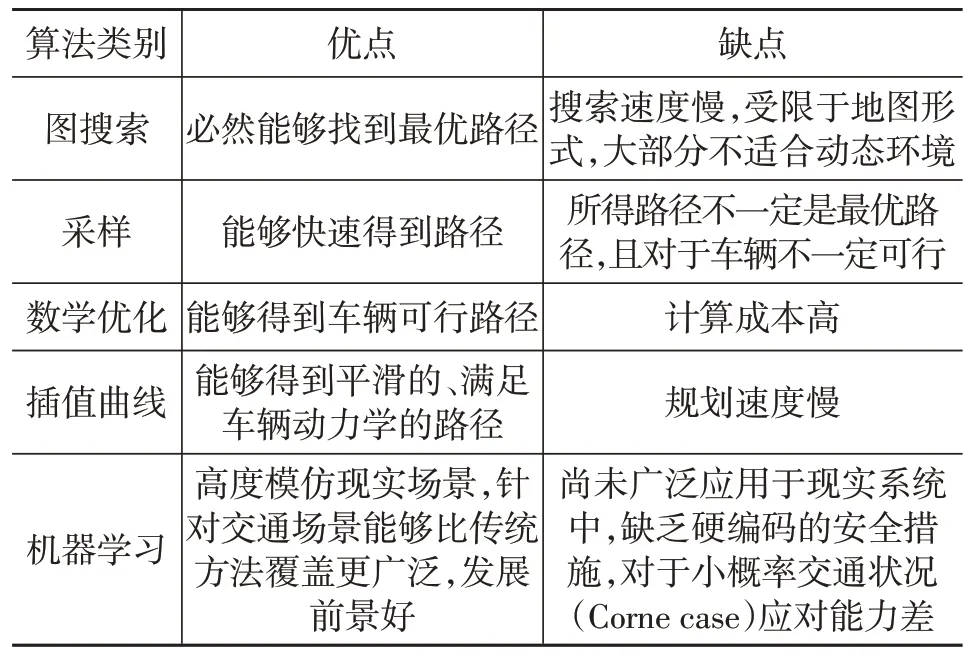
表6 轨迹规划方法比较

3 挑战与展望

本文分析了目前轨迹规划的常见方法并给出了其具体应用。虽然这些方法可以在仿真或者部分固定场景中应用，但是距离5级驾驶自动化还有一定距离。

从安全性来看，虽然可以额外设计安全检测和安全回退系统来规避危险场景，如Mobileye提出的RSS责任敏感安全模型（Responsibility Sensitive Safety，RSS），可以对场景和规划路径进行安全评判。但是从本质上来说，这种方法没有从规划算法本身考虑安全问题。

实时性对自动驾驶来说至关重要，在真实动态场景中，如何在单车有限算力情况下提高规划算法运行效率是个值得研究的问题。在5G 网络出现后，可寄希望于云端强大的算力来解决这一问题，目前基于车、路、云系统的自动驾驶系统也逐渐成为研究重点。

从舒适性角度来说，这些算法大部分仅仅对轨迹进行了简单的运动学约束，没有考虑不同驾驶员的驾驶风格，未来可在进一步考虑驾驶者及乘客的舒适性，设计符合不同驾驶风格的轨迹规划算法。

在真实应用中，传感器的精度和感知范围有限，甚至大部分目标被城市中的高楼等遮挡，因此对于自动驾驶车辆来说环境是部分可观测的。如何更好地解决这种未知性和环境高交互性也是一个巨大挑战。

目前轨迹规划算法设计大多处于仿真测试阶段，对于室外真实交通环境下的轨迹选择，以及结合交通规则和驾驶者意图的协调处理仍存在很大空白。

机器学习方法应用到自动驾驶领域的时间尚短，但体现出了它独有的优势，计算机比人类更有能力持续关注和集中注意力，而随着人工智能所达到的水平越来接近完全自动驾驶所需要的智能水平，机器学习的优势也会更加明显。

目前，汽车驾驶辅助系统的研究已被广泛应用并趋于成熟，V2X的相关规范也日渐完善。自动驾驶的发展不应局限于研究自车本身，依靠自车的感知、规划来做出相应的决策，而是应该与V2X通信模块相结合，实现车路协同，通过路侧单元的感知作为自车输入，更快地实现端到端的解决方案。

除了技术问题，随着自动驾驶的发展也衍生出了责任认定、事故理赔及伦理问题，这些问题的解决需要以政府为主导，制定自动驾驶汽车发展框架、标准和法规，规范和引导相关机构行为。