基于自由扩散下被捕食者-捕食者模型的图灵不稳定分析

赖 婷，袁 权，杨喜艳，王浩华，4

（1.海南大学 理学院，海南 海口，570228；2.广东金融学院 金融数学与统计学院，广东 广州，510521；3.海南省工程建模与统计计算重点实验室，海南 海口，570228；4.海南大学 热带特色林木花卉遗传与种质创新教育部重点实验室，海南 海口 570228）

被捕食者-捕食者模型通过定义所谓的功能性函数来描述捕食者在单位时间内消耗被捕食者的数量，以此来刻画生态系统中不同物种之间存在的相互作用［1-4］.作为该类模型的一个关键性因素，Holling［5］提出了3种不同类型的功能反应函数来模拟被捕食者-捕食者模型，大量结果表明，Beddington-DeAngelis功能反应更能贴近真实的种群行为特征［6-9］.此外，生态系统中物种间相互作用在空间上的行为特征引起了学者的广泛关注.自Turing［10］提出反应-扩散系统以来，反应-扩散系统已被广泛研究.交叉扩散问题首先由Kerner［11］提出，Shigesada 等［12］将交叉扩散问题应用于竞争种群系统中，刻画种群在相位空间中的相对联系.在自然界中，考虑到被捕食者之间存在自由竞争而导致自相残杀或同类相食的情况，大多数雄性动物为了种群繁衍，扩大种群数量，会找多个雌性动物繁衍后代，因此会导致同类争夺配偶的情况发生，例如，眼镜蛇.由于生物种群之间的自扩散和交叉扩散的普遍存在性，不同于文献［13］，笔者考虑了具有Beddington-DeAngelis 功能反应且种群之间具有自扩散和交叉扩散模式下的被捕食者-捕食者模型.假定被捕食者具有Logistic增长及种群内部自由竞争，且该种群在空间中自由扩散.首先给出了系统满足耗散性和一致持久性的充分条件，并对系统的非负平衡点进行稳定性分析和图灵不稳定性分析，然后确定产生图灵斑图的分岔参数满足的条件，并由此识别出图灵区域，最后通过Matlab软件进行数值模拟，选取不同的分岔参数可以观察到，分岔参数会影响种群的动力学形态.通过数值模拟结论表明，系统产生的图灵模式主要分为2 种：1）斑点模式遍布整个空间；2）条纹模式和斑点模式共存.但后者经过时间的推移，条纹分裂成斑点，最终以斑点模式遍布于整个空间为稳定的动力学形态.

1 模型建立

在自然界中，物种的生长与其自身的数量以及相关物种的数量有关.前人对形如以下模型的动力学行为的研究已做了大量的工作，主要考虑Beddington-DeAngelis 功能反应，被捕食者具有Logistic增长［14-15］：

基于系统（1），考虑了被捕食者存在种群内部自由竞争的情形，即被捕食者除了在Logistic 增长条件下受到环境承载率约束而导致食物、空间等资源的不足而产生的种内竞争外，还存在种群内部的自由竞争，得到如下模型

其中，U(t)，V(t)分别代表在t时刻被捕食者和捕食者的密度，r，K，h，e，c，d 为正常数，分别代表物种的内在增长率，被捕食者的环境承载率，被捕食者之间的种内竞争，被捕食者转化为捕食者的转化率，被捕食者的死亡率以及捕食者的死亡率称为Beddington-DeAngelis 功能反应，参数a为被捕食者的最大消耗率，用参数b来衡量被捕食者干扰的影响.

对于模型（2），令

则模型（2）简化成以下无量纲形式的模型（3）

通过改变自变量dτ→(β+u+v)dt，得到与模型（3）对应的模型（4）

分别记模型（4）的第一个方程为f(u，v)，第二个方程为g(u，v)，为了研究模型（2）的空间动力学，将模型（2）

转化为研究模型（4），基于模型（4），考察如下自扩散和交叉扩散模型

其中，∇2=∂2/∂x2+∂2/∂y2是二维空间中的拉普拉斯算子，描述了物种间的随机运动，其中非负常数d11和d22分别为被捕食者和捕食者的自扩散系数，d12和d21分别为被捕食者和捕食者的交叉扩散系数，可能取正值或零，取正值表示一个物种向另一个较低密度的物种方向扩散［16］，主要考虑交叉扩散和自扩散同时存在的被捕食者-捕食者系统.

对于模型（5），在给定的初始条件和零通量条件［17］下进行分析.

其中，LX和LY分别表示系统在X，Y方向上的大小，n表示∂Ω的向外单位法向量，零通量意味着没有其他种群通过边界.

2 系统的耗散性

从生物学的角度来看，耗散性意味着所有的种群都是有界的.将证明系统（3）的耗散性.在证明耗散性之前先给出2个引理，引理的证明前人已经给出［18］.

定理1当δ-μ＞0时，系统（3）是耗散的.

证明对于系统（3）的第一个方程，可得

设δ-μ＞0，然后使用引理2，并假设存在一个正实数M1，可得

因此，对于ε1＞0，存在一个T1＞0，对于任意的t＞T1有，u(t) ≤M1+ε1.

现在，对于任意的t＞T1有，

其中，G=(δ-μ+ω)(M1+ε1).

因此，使用引理1，可得

现在假设存在正实数M2，可得

因此，对于ε2＞0，存在一个正实数T2＞T1，对于任意t＞T2可得v(t) ≤M2+ε2.

综上可知，当δ-μ＞0时，系统（3）是耗散的.

3 系统的一致持久性

一致持久性在生物学意义上保证了物种的长期生存.从分析学的角度来看，一致持久性的定义如下：

定义1如果系统（3）的每个初始条件为(u(0)，v(0)) ∈int()的解(u(t)，v(t))都满足以下条件，则说系统（3）是一致持久的.

1）u(t) ≥0，v(t) ≥0对于∀t≥0.

2）存在ε＞0，使得成立.

定理2当δ-μ-1 ＞0和(γ-ω)(m1-ε3) ＞ωβ时，系统（3）是一致持久的.

证明从系统（3）的第一个方程可得，对于任意的t＞T2，

4 非负平衡点的稳定性分析

为了研究图灵不稳定性，考虑模型（4），通过计算，得出3个非负平衡点：

定理3当δ-μ＞0时系统（4）在平衡点E1处不稳定，反之，系统（4）在E1处稳定.

证明在稳定点E1处的雅可比矩阵为

由此可知，J(0，0)的特征多项式为f(λ)=(λ-δβ+μβ)(λ+ωβ)，特征值分别为λ1=(δ-μ)β，λ2=-ωβ，当δ-μ＞0 时，系统（4）有一个正根(δ-μ)β和一个负根-ωβ，所以系统（4）在E1点处不稳定.从生物学的意义上来说，在系统（4）中，所有物种都不可能全部灭绝.反之，若δ-μ＜0，则系统（4）的特征多项式有2个负根，故系统（4）在E1点处稳定.

定理4当β＞时，系统（4）在平衡点E2处局部渐近稳定，反之，系统（4）在平衡点E2处不稳定.

证明通过计算系统（4）在平衡点E2处的雅可比矩阵可知

根据前人的研究，在不带有扩散项的常微分方程中，稳态是稳定的.在带有交叉扩散的偏微分方程中稳态是经过非均匀扰动从稳定状态到不稳定状态，从而产生图灵模式，给出系统（4）稳态稳定的条件［19］

定理5当tr(JE*) ＜0，且det(JE*) ＞0时，系统（4）在正平衡点E*=(u*，v*)处局部渐近稳定.

证明求出系统（4）在稳定点E*处的雅可比矩阵，雅可比矩阵在上文中已经给出，当

可以得到，矩阵A的2 个特征根都为负值，由此可知，系统（4）在稳定点E*处局部渐近稳定，通过计算，可以得到

综上可知，当a11+a22＜0，a11a22-a12a21＞0时系统（4）在正平衡点E*处局部渐近稳定.

5 图灵不稳定性分析

考虑系统（5）在正稳态E*处的图灵不稳定性，将系统（5）在E*周围线性化，对于依赖于空间和时间较小的扰动［19］

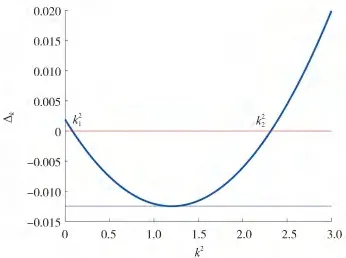
图1 波色数限制产生图灵不稳定性的范围

为了观察图灵区域，设置参 数α=0.1，δ=0.5，γ=0.8，ω=0.3，μ=0.03，d11=0.01，d21=0.001，d22=1.

现在讨论由参数β以及d12张成的空间，如图2所示.

图2 系统（5）的分岔图

图2 中绿色的直线代表Hopf 分岔，对应的Hopf 分岔参数值为βT=0.027 4，红色的曲线代表Turing 分岔.区域Ⅳ表示图灵区域，此区域中找到的稳定点在非均匀扰动下是不稳定的，因此可以观察到图灵斑图.区域Ⅰ表示具有齐次均衡的系统是无条件稳定的.区域Ⅱ表示只存在Hopf 不稳定性.区域Ⅲ表示稳定点有可能发生图灵不稳定性也有可能发生Hopf不稳定性.

保持其他参数不变，改变β值，得到不同分叉参数β对应的色散关系，如图3所示.

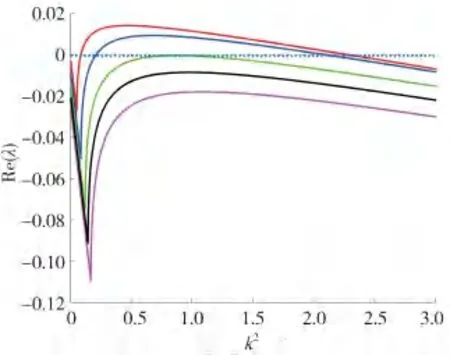
图3 不同的分叉参数对应的色散关系

图3 中从下到上的第三条曲线对应的临界参数值βT=0.110 311 177 473 585，当β＜βT时，图灵不稳定性发生，反之，当β＞βT时，不会发生图灵不稳定性，即系统的稳态是稳定的.β的值从图3中的曲线从下到上分别取β=0.15，0.13，0.110 311 177 473 585，0.08，0.05，从图3 中也可以看出，波色数在(0.055 9，2.342 1)区间内，会发生图灵不稳定性，这与图1相对应.

6 数值模拟

通过绘制图4 观察系统（4）的稳定性，设置参数为α=0.1，δ=0.5，γ=0.8，ω=0.3，μ=0.03，β=0.05，蓝色和红色曲线的初始值分别为(0.05，0.08)，(0.15，0.20).通过计算得出a11a22-a12a21=0.001 9，a11+a22=-0.005 4，从图4 可以观察到，无论被捕食者与捕食者种群密度的初始值取何值，系统最终都会趋于稳定，定理5得到验证.

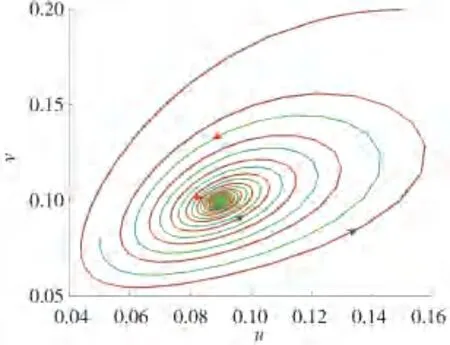
图4 系统（4）趋于稳定

通过绘制图5 观察2 个种群数量关系的变化，图5a、b 和c 为系统（3）的种群密度关系变化图，图5d 为系统（1）的种群密度关系图.图5a结果表明，控制被捕食者种内竞争的变量α=0.1时，被捕食者与捕食者密度变化出现同增同减，且以时间t为周期的周期震荡现象.图5c结果表明，当α=20，由于被捕食者种内竞争强度增强导致种群数量急剧下降，从而使得捕食者由于缺乏食物导致种群数量减少，当捕食者数量减少到一定程度时，被捕食者数量开始少量增长，并趋于平衡，捕食者由于食物严重匮乏而出现衰亡现象.对比图5a与图5c发现，被捕食者种内自由竞争的强度增强，捕食者由于食物匮乏导致衰亡，种群密度以时间t为周期的周期震荡现象消失.

图5 2个种群的数量关系

图5b 结果表明，随着时间的推移，种群密度变化趋于平稳，系统逐渐稳定，被捕食者与捕食者共生存.图5d结果表明，被捕食者与捕食者密度变化也会出现同增同减，以时间t为周期的周期变化现象.对比图5b与d发现，图5d中被捕食者与捕食者的种群密度都比图5b中2个种群的种群密度大，说明系统由于存在被捕食者的种内自由竞争从而导致被捕食者与捕食者的种群数量减少.

在图灵斑图的数值模拟中，需要将系统的空间和时间离散化，即从无限维变换为有限维的形式.在实际应用中，反应扩散系统在二维空间中的连续问题在M×N网格点的离散域内求解.网格的长度设置为常数h，时间步长设置为常数τ，描述扩散的Laplacian 算子采用有限差分法进行求解，对于模型（5），在(xi，yi)位置上的进行迭代，有如下形式

其中，Laplacian算子为

同样地，也可以写出∇2Φ2.设置网格步长h=0.15，时间步长τ=0.001 以及网格大小M=N=220，并且设置固定的参数值为α=0.1，δ=0.5，γ=0.8，ω=0.3，μ=0.03，d11=0.01，d12=0.58，d21=0.001，d22=1，初始值为在稳定点E*附近均匀分布的随机扰动，记为

其中，η1(x)，η2(x) ∈[-5×10-5，5×10-5]，通过改变β的值进行数值模拟，直到其行为特性不再改变时停止，观察被捕食者种群的斑图.数值模拟的结果如图6所示.

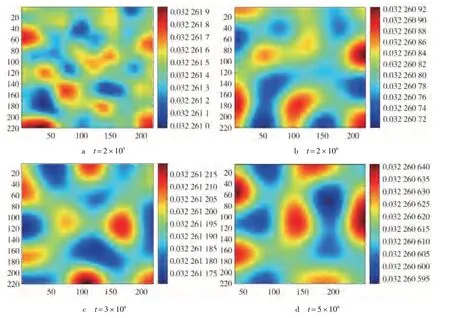
图6 β=0.015时被捕食者的图灵斑图

从图6 可以看出，图6a 由于迭代时间较少，在随机扰动的作用下，形成不规则的图案，随着迭代时间的逐渐增大，系统逐渐形成斑点模式且最终斑点模式不再改变.

图7为β=0.02，迭代时间分别为t=2×104、t=1×106、t=2×106、t=5×106所呈现的图灵斑图.

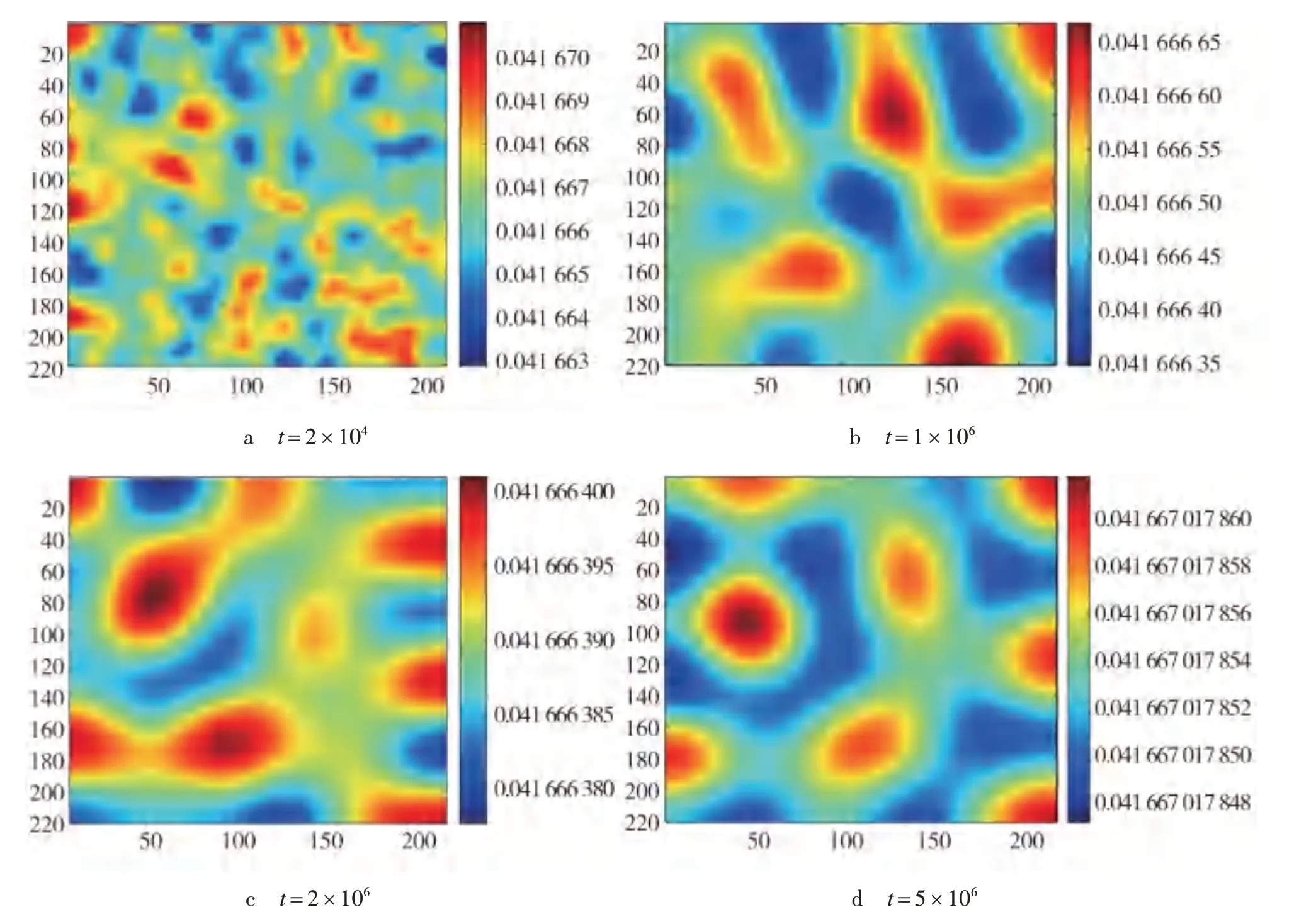
图7 β=0.02时被捕食者的图灵斑图

同样地，在图7 a 中，由于迭代时间较少，在随机扰动的作用下形成不规则的图案，随着时间的推移，系统开始形成长度较短的条纹模式，条纹随着时间的增加长度逐渐增长，并趋于分裂，且空间中出现斑点，最后形成形态稳定的斑点图.对比图6 和图7，可以看出，改变分岔参数β，会导致系统呈现出不同的图灵模式.

7 小 结

研究了具有Beddington-DeAngelis 功能反应和自扩散以及交叉扩散的被捕食者-捕食者模型的空间动力学模式，在经典的被捕食者只具有Logistic 增长模型上，考虑了被捕食者存在种群内部自由竞争的情形，即被捕食者除了在Logistic 增长条件下受到环境承载力约束而导致的食物、空间等资源不足外，种群内部还存在自由的竞争形态.首先分析了系统满足耗散性以及一致持久性的条件，其次对系统的3 个非负平衡点进行稳定性分析以及图灵不稳定性分析，给出了产生图灵不稳定的条件，通过图灵不稳定性分析发现，波色数、分叉参数、扩散系数都会影响系统图灵不稳定性的发生，从而影响图灵斑图的空间形态，在数值模拟中也验证了这一点.同时，在数值模拟中可以清晰地看到，2个种群的数量关系呈现出以时间为周期的周期震荡现象，随着时间的推移，2 个种群数量最终趋于稳定，被捕食者与捕食者共生存.除此之外，通过图5 的结果及分析表明，被捕食者存在种内自由竞争会导致被捕食者与捕食者种群数量减少，且当被捕食者种内竞争强度增大时，会导致捕食者因食物严重匮乏而衰亡，且种群数量以时间为周期的周期震荡现象消失.