一种基于压缩感知理论的强反射地震信号消减方法

2023-07-08李胜军高建虎张繁昌贺东阳桂金咏

岩性油气藏 2023年4期

李胜军，高建虎，张繁昌，贺东阳，桂金咏

（1.中国石油勘探开发研究院西北分院，兰州 730020；2.中国石油大学（华东）地球科学与技术学院，山东青岛 266580）

0 引言

由于地震工区沉积环境的特殊性和复杂性，地震数据中通常存在强反射背景，如灰质成分或因泥岩脱水等作用形成的高速层反射、煤系地层反射等。这种强反射背景通常会屏蔽来自储层的有效弱反射信息，影响储层预测效果［1-3］。即使没有强反射屏蔽，目前寻找的储层目标一般是隐蔽油气藏，其反射强度相对较弱，如果不对其进行目标增强处理，难以进行隐蔽油气藏的识别［4-6］。为此，国内外很多学者开展了强反射去除方法的研究。汪恩华［7］提出了相似背景分离法去除强反射；赵铭海［8］利用相似背景分离法开展了薄层反射特征提取研究；张军华等［9］应用多子波分解重构方法剥离了强屏蔽层；金成志等［10］引进子波主成分分解的思路，在Wheeler 域提取高频短旋回强屏蔽信息，实现了强屏蔽的剥离；王宝江等［11］使用广义S 变换进行含煤地层砂体预测；王大兴等［12］给出了一种基于经验模态分解的最大能量法消除煤层引起的强反射；谢春林等［13］应用奇异值分解技术将常规地震数据分解成不同分量的数据集合，通过去除第一分量强反射，突出了掩盖在强反射背景下的砂岩弱反射信号；Wang［14-15］提出了基于自由多尺度的匹配追踪去除强屏蔽的方法，利用地震时频谱分解实现强屏蔽的剥离，随后又发展了多道匹配追踪算法来解决强屏蔽的横向连续性问题；李海山等［16］提出了匹配追踪煤层强反射分离方法，有效去除了煤层强反射；徐璐等［17］采用基于局部频率约束的动态匹配追踪强反射识别方法，削弱了高阻层强反射干扰的影响；杨子鹏等［18］给出了一种多道联合约束的匹配追踪强反射轴压制方法，实现了强反射轴中及其附近有效信号的识别；张生强等［19］提出一种基于地震相位分解的强反射分离方法，在去除特殊围岩等因素产生的强反射干扰相位分量的同时，突显了目标储层。分析发现，这些方法大都需要假定强反射的波形形状，或者事先给出强反射波形，不太适用于强反射波形横向变化较大的情形。现有方法去除强反射的过程是沿着强反射层位进行的，需要准确的强反射层位解释数据，而当层位数据不准确时，会影响强反射消减结果的准确性。

基于地震强反射和目标弱反射的子波干涉机理，利用动态字典逼近法将任意波形的强反射从地震数据中提取出来，然后基于屏蔽函数将强反射波形从地震记录中减去，以期消除强反射背景的影响，提高地震解释和储层预测的精度。

1 方法原理

地震剖面中强反射屏蔽的消减，首先要把强反射波形分离出来，然后再按照某种准则进行消减。此次研究基于压缩感知理论，根据地震强反射的波形特点创建动态雷克子波字典，将地震强反射波形分解为变换基的稀疏表示［20-21］。在波形重构时通过创建强反射屏蔽函数，压制大的动态字典分量来消减强反射，同时保持地震同相轴的横向连续性。

1.1 压缩感知任意波形强反射分解方法

压缩感知的核心是信号的稀疏表示［22-23］。将有限长离散时间信号x看作实数RN空间的列向量，RN中的任意信号都能用N×1 维基向量线性表示。把组合成N×N矩阵Ψ，则有

式中：Ψ为变换基或字典；θ是N×1 维系数向量，同时是信号在Ψ域的表示；x是信号在时间域的表示。当θ中的非零元素个数比N小很多时，信号在Ψ域中是稀疏的。

利用压缩感知理论分解强反射信号包括以下3步：第1 步为信号稀疏表示，即信号x在Ψ上的表示是稀疏的；第2 步，根据实际问题构建合理的基矩阵Ψ；第3步，求出稀疏系数θ。概括来说就是变换基的构建和稀疏系数求解方法。

（1）变换基的构建

地震信号可以表示为反射系数和子波的褶积，雷克子波是地震解释中最常用的子波，因此用雷克子波作为母函数［24-25］。由于事先并不知道强反射在地震剖面上出现的位置，也不知道强反射波形的形状，因此，根据强反射波形的特点，此次研究建立基于雷克子波母函数的动态字典作为变换基。

（2）稀疏系数的求解向量lp的范数表达式为

当p=0 时，N表示θ中所含非零元素的个数，因此，零范数是稀疏性最直接的度量［26-28］。考虑到强反射附近的地震数据量不大，所以采用零范数度量地震数据的稀疏性。这样，若信号x在Ψ域中稀疏，则优化问题的目标函数为

其中，k为阈值，即非零元素的最大个数。

每次迭代时，根据强反射信号的强弱和位置构建动态字典，再通过奇异值分解计算动态字典中每个分量的系数即可。求解获得稀疏系数θ后，利用式（1）即得到强反射附近地震波形的最佳逼近。

具体来说，利用压缩感知理论提取强反射波形的算法如下：①对包含强反射的地震数据，给定包含强反射的时窗范围、地震数据主频、稀疏性约束阈值k，强反射门限值等参数；②以雷克子波为母函数创建变换基矩阵，雷克子波主频为第①步给定的地震数据主频，基矩阵行数和列数均为第①步时窗范围所包含的采样个数；③设稀疏系数θ初始值为0；④搜索给定时窗范围内的地震波形极值点，若极值点振幅的绝对值大于第①步给定的强反射门限值，则标记这些强振幅的位置；⑤根据第④步标记的位置，提取基矩阵中的相应分量形成动态字典，通过求解公式（3）得到这些位置的系数值；⑥根据公式（1）计算强反射地震数据，并从实际地震数据中减掉，得到二者的残差数据；⑦若残差数据中含有高于强反射门限值的振幅值，则转第④步继续迭代，若残差数据不再含有高于强反射门限值的振幅值，则停止迭代，输出强反射结果；⑧对三维工区中的每一地震道进行步骤③至步骤⑦的循环，直到所有数据计算完毕。

1.2 基于屏蔽函数的强反射消减

对强反射周围的地震信号压缩感知分解后，可把动态字典中振幅较大的分量切除，达到去强反射的目的。但是，若将所有动态字典分量用给定的门限值作为常系数进行消减，会造成强反射消减后的地震剖面产生锯齿状痕迹（图1）。对比强反射消除前后的地震剖面可以看出，通过设定一个门限值作为常系数，振幅大于该值的分量均去除后的地震剖面上在强反射同相轴附近产生了强烈的竖向锯齿。为解决这个问题，受吉布斯现象的启发［29］，本文采用基于屏蔽函数的方法消减强反射，屏蔽函数为

图1 实际资料采用不同方法去除强反射前、后地震剖面对比Fig.1 Comparison of seismic sections before and after strong reflection removal by different methods

式中：A为动态字典分量振幅值；Al和Ar分别为左门限值和右门限值。对振幅小于左门限值的动态字典分量均予以保留；对振幅大于右门限值的动态字典分量均予以去除；对振幅介于左右门限值之间的分量做部分去除，振幅越小的分量保留越多，振幅越大的分量去除越多，而不是“一刀切”。通过屏蔽函数法去除强反射后，解决了常系数法消减强反射出现的锯齿问题，改善了强反射消减效果。

2 模型测试

2.1 数值模型数据去强反射

为了验证屏蔽函数法去强反射的有效性，根据鄂尔多斯盆地煤层资料建立强反射模型。地震数据主频为30 Hz，第1 层泥岩速度为4 200 m/s，厚度为150 m；第2 层煤层速度为2 700 m/s，厚度为12 m；第3 层泥岩速度为4 250 m/s，厚度为338 m。在模型的第3 层中设计从右至左距离界面依次为λ（λ为波长），3λ/4，λ/2，3λ/8，λ/4，λ/8，λ/16，λ/32 及λ/64 的块状砂体储层，速度均为4 900 m/s，厚度为5 m。利用褶积模型法合成的地震剖面（图2a），煤层强反射位于0.05～0.10 s，从剖面上可看出，下伏储层的响应在距离煤层小于λ的情况下，受强反射影响，砂体很难有效识别。通过基于屏蔽函数的强反射消减分离出的强反射信号（图2b）与某商业软件处理获得的强反射信号（图2c）看上去差别不大，但对比2 种方法消减强反射后的地震剖面（图2d，2e）可看出，本文方法比商业软件的处理结果从第420 道向右的地震道上同相轴横向连续性偏好，强反射同相轴消减得也更彻底，被强反射屏蔽的块状砂体弱反射显现出来，而某商业软件去除强反射后的地震剖面上的强反射仍有较多残留。

图2 模型数据采用不同方法去除强反射前、后的地震剖面对比Fig.2 Comparison of seismic sections before and after strong reflection removal by different methods of numerical model

需要说明的是，商业软件去强反射的方法必须沿着强反射层位数据匹配强反射。在本例中，为去除强反射，需要拾取T1 和T2 层位数据（图2c），先去除沿着T1 层位的强反射，再去除沿着T2 层位的强反射。本文方法在去除强反射时，是对给定时窗内的地震数据进行强反射消减。例如，强反射同相轴位于0.05～0.10 s，可以给定0.05～0.10 s 的时间窗，也可以沿T1（或T2）取时窗，只要给出包含强反射的时窗即可，不需要准确的层位数据，且可将时窗范围内的强反射一次处理完成。

对比去除强反射前、后的地震剖面，可见当砂体与强反射层距离大于或等于λ时，强反射同相轴对下伏砂体无屏蔽作用；当砂体与强反射层距离小于λ时，强反射屏蔽的影响得以消减，但距离不同消减程度不同，其中砂体与强反射层距离大于λ/4时，强反射可被完全去除，弱反射完全显现；当砂体与强反射层距离小于λ/4 时，在砂体弱反射干涉部位的强反射能量有残余，且砂体与强反射层距离越小，特别是小于λ/8 时，强反射能量很难被彻底去除（图3）。

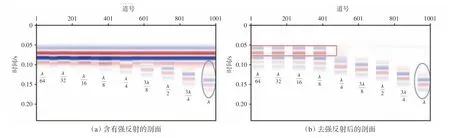
图3 数值模型中基于屏蔽函数的强反射消减法应用效果分析Fig.3 Analysis of strong reflection removal results based on shielding function in numerical model

2.2 物理模型数据去强反射

为检验屏蔽函数法去强反射是否适应横向变化的强反射屏蔽消减，利用物理模型数据进行测试。用于测试的物理模型尺寸为1.2 m×1.2 m×1.4 m，与实际地层的对应比例尺为1∶10 000，模型相关参数如表1 所列。在低速层2 的下伏地层内有5 个直流河道砂体，河道砂体速度均为2 600 m/s，密度均为1.31 g/cm3，垂向厚度均为30 m，横向宽度均为100 m；各河道砂体中心的横向间距为500 m。设置地震主频为60 Hz，波长λ为40 m，从左向右各河道砂体与煤层底界面的距离依次递增，分别为0 m，10 m（λ/4），20 m（λ/2），30 m（3λ/4）和40 m（λ）。

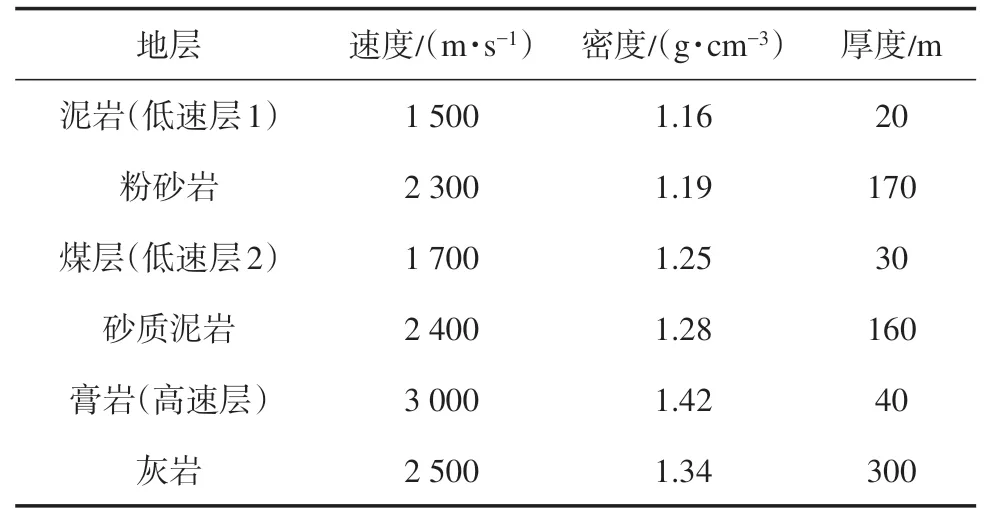
表1 物理模型参数Table 1 Parameters of physical model

物理模型数据的处理时窗1.54～1.65 s 内的地震记录包含河道砂体目的层段信息，地震主频为60 Hz，波长为40 m。强反射消减前，由于煤层与其相邻地层的阻抗差异大，在地震剖面上产生了强反射同相轴，河道砂体弱反射信息被屏蔽，虽然可以看到部分河道砂体的微弱响应，但其展布难以在地震剖面上清晰识别（图4a）。由于剖面上强反射同相轴无论是旅行时还是波形在横向上都是变化的，进行强反射消除时先进行反射同相轴的拾取（剖面上绿色线），再沿绿色层位线取时窗进行强反射消减，分离出强反射信号（图4b），最后得到强反射消减后的剖面（图4c）。处理前、后的剖面对比可见，剖面上横向变化的强反射得到很好地消除，同时被强反射屏蔽的河道砂体弱反射信息（图4c 中蓝框所示）显现出来，砂体边界更加清晰。当河道砂体与煤层底界面距离为λ时，强反射消减前、后，河道砂体的反射在地震剖面上均可识别，但在强反射消减后的剖面上更清晰；当河道砂体与煤层底界面距离小于λ且大于λ/4 时，强反射消减前，河道砂体的反射信息被掩盖，且随着距离的减小，在剖面上几乎无法识别，而强反射消减后，可识别河道砂体的弱反射信息；当河道砂体与煤层底界面的距离为零时，强反射消减前，河道砂体反射信息被强反射掩盖，强反射消减后也得到一定程度显现。

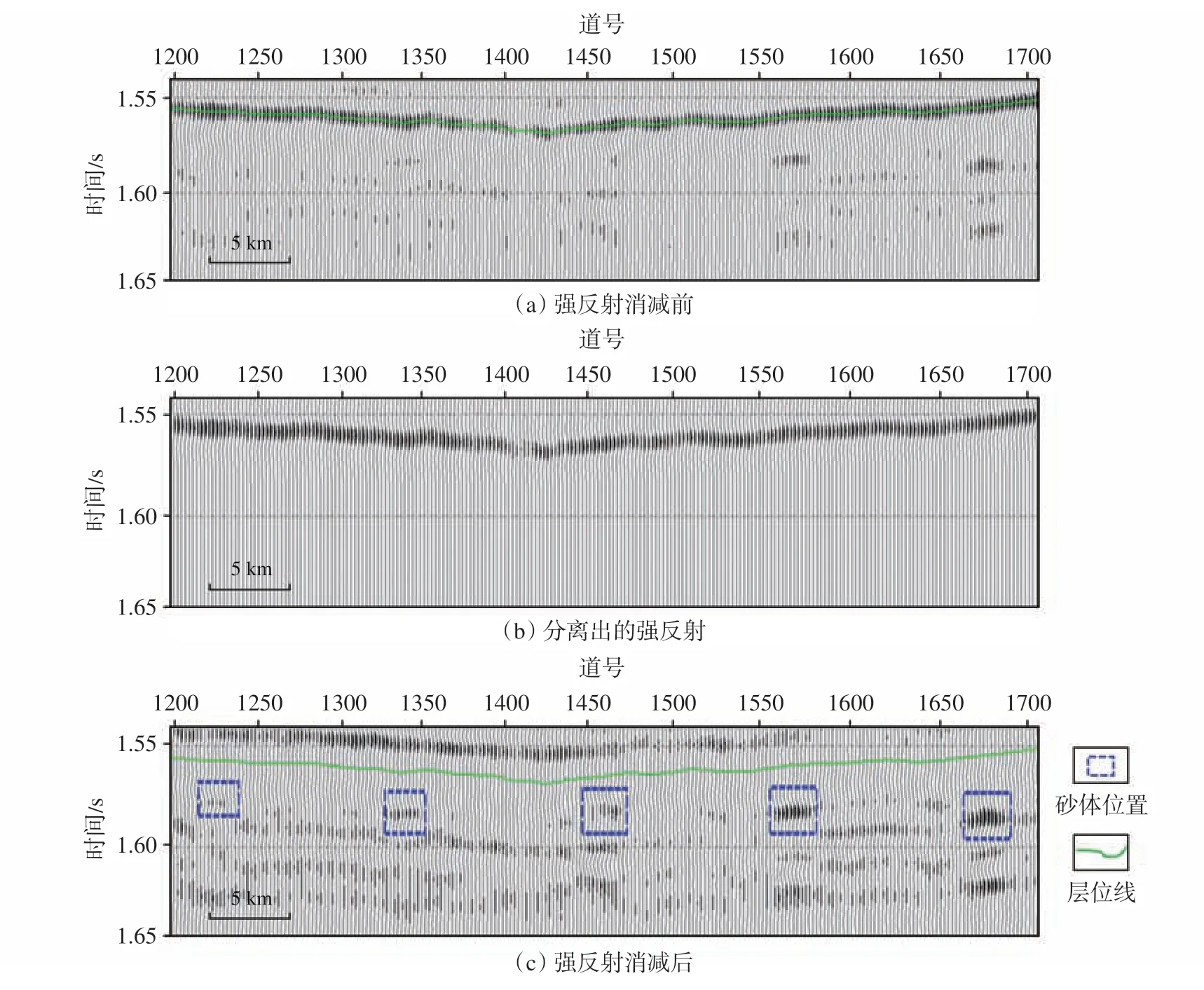
图4 物理模型数据强反射去除前、后地震剖面对比Fig.4 Comparison of seismic sections before and after strong reflection removal of physical model

为了从平面上更直观地分析强反射消减效果，对处理前、后的数据体提取沿强反射层位向下16 ms 时窗内的均方根振幅切片。切片对比可见，在强反射消减前，河道砂体信息被屏蔽，难以识别（图5a），而煤层强反射消减后，5 个直流河道砂体在平面上清晰可见（图5b）。

图5 物理模型数据强反射消减前（a）、后（b）均方根振幅切片对比Fig.5 Comparison of RMS amplitude slices of physical model data before（a）and after（b）strong reflection removal

3 实际应用

此次应用的研究工区位于四川盆地川中古隆起构造带中部，目的层二叠系茅口组为高速灰岩层，上覆龙潭组为低速泥页岩［30］。从井震剖面上A井的波阻抗曲线（图6 中红色曲线）可以看出，由于2 套地层之间巨大的波阻抗差异，在茅口组顶界面（简称茅顶）形成了强反射，茅顶附近的储层弱反射被屏蔽，几乎一片空白。

图6 四川盆地川中古隆起构造带中部过A 井二叠系茅口组顶界面强反射地震剖面Fig.6 Seismic section with strong reflection across well A in the central uplift tectonic zone of central Sichuan Basin

提取目的层茅二段储层的地震振幅切片（图7）可见，由于工区南部、北部茅二段储层距茅顶较近，受强反射影响较大，储层反射几乎被完全屏蔽，例如红色椭圆内的A 井区；中部距茅顶较远，能够识别部分储层反射，例如黑色椭圆内的B井区。

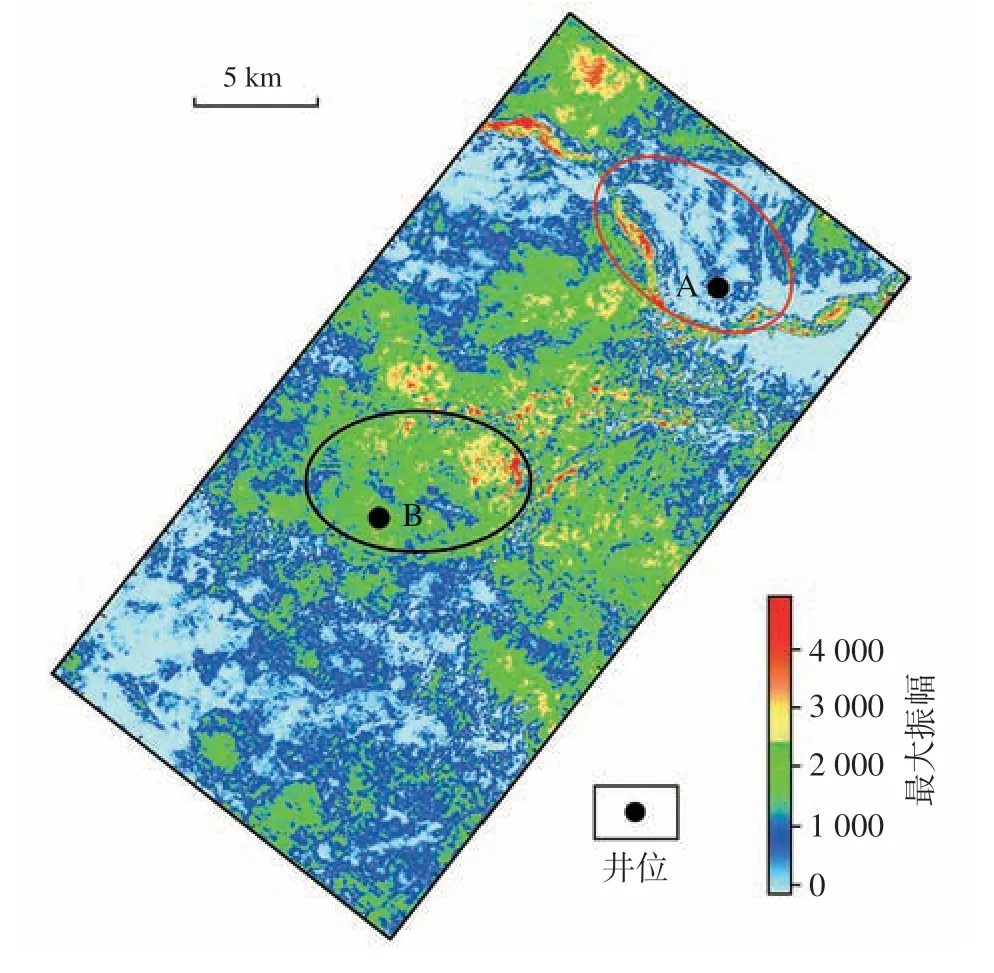
图7 四川盆地川中古隆起构造带中部二叠系茅口组二段储层地震最大振幅切片Fig.7 Maximum amplitude slice of reservoir of the second member of Permian Maokou Formation in the central uplift tectonic zone of central Sichuan Basin

研究区目的层地震主频为22 Hz，地层速度为6 200 m/s，1/4 波长为70.5 m。分别对A 井和B 井进行井-震联合分析（图8），A 井储层与茅顶距离为67 m，小于1/4 波长，储层反射完全被屏蔽；B 井储层与茅顶距离为111 m，大于1/4 波长，储层反射受茅顶强反射的影响小。茅二段在平面上，南部和北部几乎没有储层反射信息，而中部仅有部分反射信息，与前述数值模型、物理模型数据的分析结果吻合度高。

图8 四川盆地川中古隆起构造带中部2 口井二叠系茅口组二段储层井-震联合分析Fig.8 Combined logging and seismic analysis of reservoir of the second member of Permian Maokou Formation of two wells in the central uplift tectonic zone of central Sichuan Basin

利用本文方法对茅顶强反射进行消减，强反射消减后的剖面上茅二段储层响应得到增强（图9 箭头所指）。为了整体对比强反射消减效果，在同样时窗内提取强反射消减后茅二段地震最大振幅切片（图10），可见，茅二段南部、北部储层的地震响应得到恢复，如红色椭圆内的A 井区，储层弱反射得以显现；黑色椭圆内B 井区的储层响应虽未被完全屏蔽，去强反射后也得到增强。总体而言，工区茅顶强反射消减后，更有利于分析茅二段储层的空间展布特征。

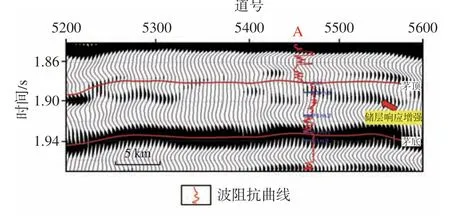
图9 四川盆地川中古隆起构造带中部茅顶强反射消减后的地震剖面Fig.9 Seismic section after strong reflection reduction of the top of Maokou Formation in the central uplift tectonic zone of central Sichuan Basin

图10 四川盆地川中古隆起构造带中部去强反射后茅二段储层最大振幅切片Fig.10 Maximum amplitude slice after strong reflection removal of the second member of Maokou Formation in the central uplift tectonic zone of central Sichuan Basin

整体而言，本方法对提高地震解释精度具有较好的效果，但需要对每一道地震强反射附近的波形进行动态字典分解，计算量大，当三维工区的道数达到百万数量级时，需要4 h 以上的计算时间。