脉冲爆震环境下涡轮性能及气热负荷的时序演变规律
2023-07-08张伟昊穆雨墨王宇凡廖湘力
张伟昊 ,穆雨墨 ,王宇凡 ,廖湘力
(1.北京航空航天大学能源与动力工程学院,2.航空发动机气动热力国家级重点实验室:北京 100191)
0 引言
爆震燃烧具有自增压、燃烧过程熵增小[1-2]、热力循环效率高[3]等特征,自20 世纪50 年代以来,研究人员一直致力于将其应用于吸气式推进系统。相比传统发动机,采用爆震燃烧代替传统定压燃烧的爆震发动机在提高发动机比推力、降低耗油率等方面均具有突出的潜力[4-5]。目前学者主要提出了3 种基于爆震燃烧的推进系统:驻定爆震发动机、脉冲爆震发动机和旋转爆震发动机。3 种构型各具优势和不足:驻定爆震发动机对来流马赫数要求高(Ma=5~7),爆震波难以长时间维持,目前尚处机理研究阶段[6];脉冲爆震发动机具有结构简单、发动机应用范围宽等优势,自21 世纪以来引起了国内外学者的普遍关注[7-9],但其有效作功时间周期占比相对较低,实际飞行可能面临推力不足等问题;旋转爆震发动机仅需一次起爆即可维持爆震工作状态,在仿真分析、模型试验等方面取得重要进展[10-11],然而在旋转爆震燃烧室内始终存在复杂的爆震波系,燃烧结构难以稳定维持,且维持时间较长的高温燃气对发动机热防护提出严峻的考验[12-13]。
早期的研究主要关注于将上述构型应用于超声速或高超声速飞行条件,如爆震冲压发动机等,一般没有旋转部件[14]。而为了在更宽速度范围内获得优异的性能,近年来国内外学者开始关注上述构型与传统涡轮发动机结合,在涡轮发动机中用爆震燃烧室代替涡轮发动机的主燃烧室或加力燃烧室,即爆震涡轮发动机[15-16]。Rasheed 等[17]结合叶栅试验和数值模拟分析了爆震波及进口参数变化对下游涡轮叶栅的影响,初步探讨了爆震波在涡轮叶栅的传播和反射过程。在涡轮性能计算方面,VanZante 等[18]和Nango等[19-20]利用3维数值模拟分析了爆震燃烧室作用下单级涡轮的时均效率,表明涡轮输出功及效率随涡轮转速增大而提高;Rouser 等[21-23]将脉冲爆震应用于向心涡轮,呈现涡轮进口回流现象和负功率输出特征。在爆震涡轮设计方面,邓芃等[24]指出了导致爆震涡轮余速损失和泄漏损失的主要原因,开展了冲击式涡轮的优化设计,优化后涡轮周期平均效率达到75%。另外,对脉冲爆震发动机涡轮性能变化规律等也开展了初步研究,但对涡轮内部流动结构演化分析只在2 维叶栅层面初步开展,对爆震波系结构时序演变的研究还存在很多空白,爆震波对涡轮气动热负荷影响的分析也存在明显不足。
本文对工作在脉冲爆震燃烧室下游的涡轮部件进行了全3 维非定常数值模拟,分析了爆震波的传播和演化规律,及在其影响下涡轮流场时空演化以及涡轮气动性能的时序变化规律,并初步探讨了涡轮非定常气动激振力及热负荷的周期性变化。
1 研究对象及数值模拟方法
鉴于目前并未有专门针对脉冲爆震环境设计的涡轮部件的公开数据,本文以典型高压燃气涡轮PW-E3为研究对象[25],分析其在脉冲爆震工作环境下的涡轮流场及气动性能。采用ANSYS CFX 软件求解URANS 方程组,完成爆震工作环境的高压涡轮数值模拟。对流通量求解格式设置为高精度,时间离散设置为2 阶欧拉后插。湍流模型采用SSTk-ω模型,该模型可以较为精确地捕捉壁面及流场结构,划分网格时保证壁面第1 层网格高度满足y+≈1 以满足湍流模型的要求。
爆震波传播周期与涡轮转静干涉的时间尺度接近,故需在计算中考虑转静干涉问题。通过模化转子叶型,保证转子的相对栅距不变的同时,使转静子叶片数能够尽可能约化。本文研究的单级涡轮导叶和动叶叶片数分别为24和54,模化后为24 和48,模化前后的涡轮叶型如图1所示,数值模拟计算域包含1导叶和2动叶。
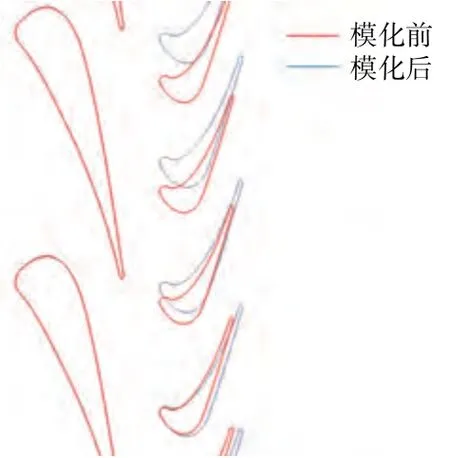
图1 模化前后的涡轮叶型
在保证第1 层网格高度满足湍流模型要求的基础上,调整网格数量,通过计算不同网格量涡轮稳态设计点性能,完成网格无关性验证。不同网格量的涡轮气动性能数值计算结果对比见表1。当网格量超过171 万后,继续增大网格量涡轮性能计算结果变化不明显,因此最终选择Grid2作为后续数值计算网格。

表1 不同网格量的涡轮气动性能数值计算结果对比
爆震涡轮的进口总压和总温设定为空间分布均匀,时间周期性剧烈变化,频率为100 Hz,即周期长度T=0.01 s。爆震计算中忽略出口静压变化,而进口参数变化规律依据Rouser 等[26]脉冲爆震涡轮测试结果以及本涡轮的稳态设计点给出,爆震涡轮进口参数时序变化规律如图2所示,图中T1*、p1*分别为进口时序变化总温和总压,T1d*、p1d*分别为相应的稳态设计点总温和总压。在计算过程中,涡轮进口参数时序变化较为剧烈的区域(0.24T~0.54T),时间步长设定为t=2×10-4T,约为转子扫掠周期的1/50,其他区域时间步长设定为t=2×10-3T。

图2 爆震涡轮进口参数时序变化规律
在爆震周期内涡轮转子转速变化范围可根据爆震涡轮的瞬态冲量距和涡轮转子盘的转动惯量估算得到。估算中忽略轴承等损失并假定压气机扭矩等于涡轮周期平均扭矩且不随时间变化。
在0~t1时刻涡轮转子转速变化量估算为
式中:J为涡轮盘转动惯量;τ为瞬态转子扭矩;上横线表示周期平均转子扭矩。
本文根据转子轴向弦长初步估算涡轮盘的轴向长度,根据轮毂平均半径估算涡轮盘的半径,涡轮盘密度根据涡轮叶盘高温合金的密度确定,从而即可估计涡轮盘的转动惯量。通过初步模拟得到最大涡轮扭矩和作用时间,估算涡轮冲量距,根据式(1)估算涡轮在0~t1的转速变化量。
本文所研究的爆震过程,爆震波对叶片影响持续时间较短,对叶片施加的冲量距相对有限,估算得到的涡轮转速变化范围在设计点涡轮转速的0.1%以内。据此,在数值模拟中忽略涡轮转子的转速变化,设定为与设计点转速一致的常量。
需要说明的是,转速变化可忽略的结论仅基于本文所研究的爆震环境和PW-E3 涡轮的响应得出,作者针对其它爆震环境或涡轮的数值模拟分析中估算得到的转速变化范围可能达到15%。对于此类爆震过程,爆震波输运导致的涡轮转速变化能否忽略还需要具体讨论。
2 爆震涡轮瞬态性能时序演化规律分析
爆震涡轮进口温度及压力呈现剧烈的时序变化,出口参数也呈现类似的变化,但由于爆震波以及波后高能量工质输运过程导致的迟滞效应,涡轮进口的参数变化无法立刻作用于涡轮通道,进出口压力测量结果峰值在相位上呈现显著差异,爆震涡轮进、出口总压测量结果的时序变化规律如图3 所示。图中p1*、p2*分别为进、出口时序变化总压,p1d*为稳态设计点进口总压,进、出口总压峰值的相位偏差量Δt=0.05T,近似于爆震波穿过涡轮通道所需时间。
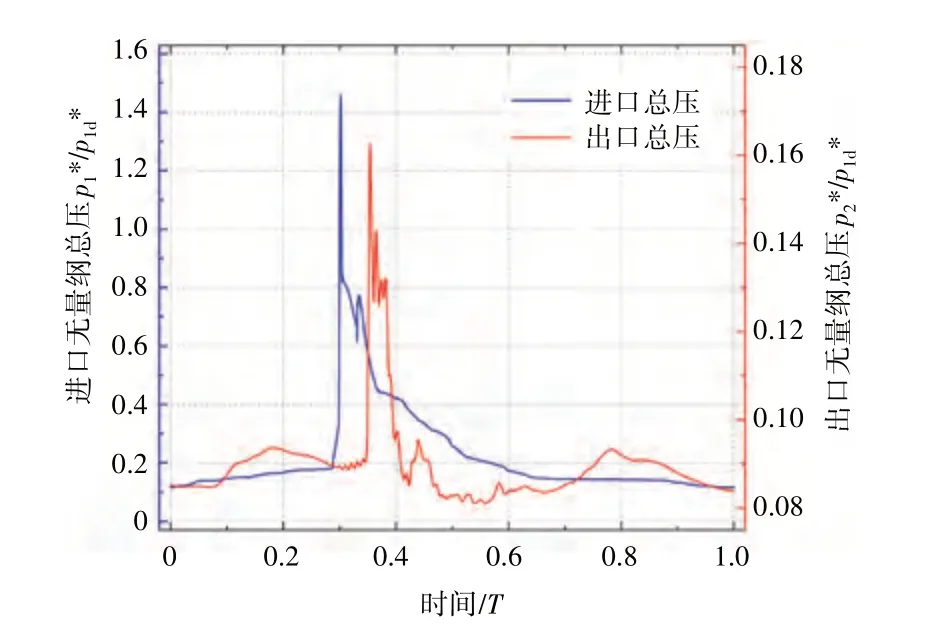
图3 爆震涡轮进、出口总压测量结果的时序变化规律
另外,从图2、3 关于进口总压的给定及测量结果对比可见,进口总压的测量结果在峰值点后的部分时间段与输入参数存在差异,该差异与爆震涡轮在对应时刻的通流特征有关。爆震涡轮的进、出口流量时序变化规律如图4所示,图中m1、m2分别为进、出口时序变化流量、md为稳态设计点进口流量。从图中可见,涡轮进口流量随着爆震波的传播过程呈现剧烈的波动,尤其在0.3T~0.6T时间段内,涡轮进口流量在正负之间波动,这与爆震波与涡轮叶片及通道的反复相互作用相关。具体而言,当爆震波进入涡轮通道时为右行激波,其传播致使涡轮进口区域处于极大的正向压力梯度,推动大量工质加速进入涡轮通道;反之,当激波与下游叶片接触并发生反射后,反射波为左行激波,这将导致涡轮进口区域处于逆向压力梯度,推动气流向上游流动,进而导致倒流现象。
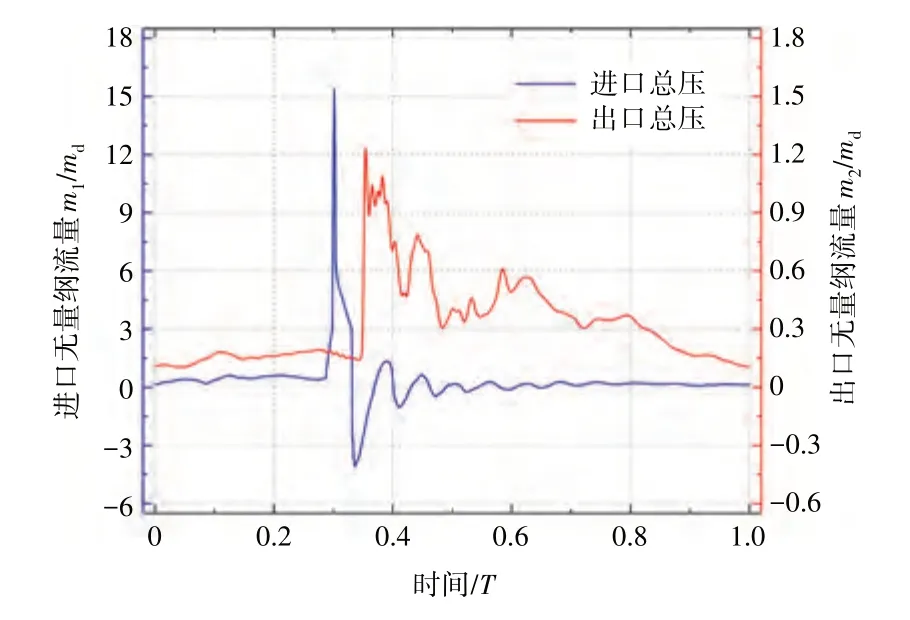
图4 爆震涡轮进出口流量的时序变化规律
爆震波的输运过程还会导致下游涡轮转子的工作状态,尤其是气流角的剧烈变化。爆震涡轮转子气流角的时序变化规律如图5 所示。从图中可见涡轮转子叶根、叶中、叶尖3 个截面进、出口气流角变化的情况。在爆震波进入转子通道之前,涡轮转子工作在大负攻角的条件下;随着爆震波后的流体进入转子通道,在高速高能量流体的冲击下,涡轮迅速由大负攻角转向正攻角,从叶根到叶尖不同截面的瞬间气流角变化可达100°~120°,落后角变化也可达到20°~30°;此后,在爆震波和反射波的反复作用下,转子进口气流角呈现剧烈波动,但整体上处于不同程度的负攻角工作状态;相比进口,出口气流角的变化幅度明显减小,但也有超过20°的波动。

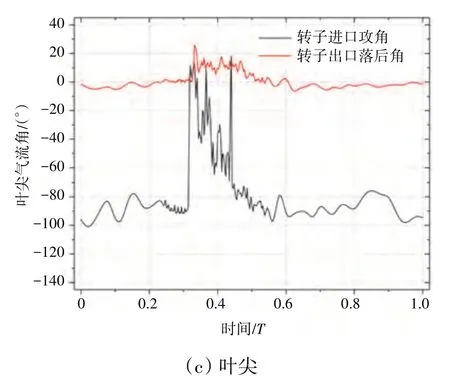
图5 爆震涡轮转子气流角的时序变化规律
上述结果表明,涡轮进、出口参数存在显著的相位差,这将导致现有的基于稳态雷诺输运定理的参数计算方法不适用于爆震涡轮瞬态参数计算(如瞬态温降及对应的瞬态功率、瞬态效率等)。如何准确评价爆震涡轮的瞬时性能也是本领域的难点之一。一种简单的瞬态性能评价方法是假定进、出口总压峰值点处于同一相位,或假定实际功和等熵功峰值点处于同一相位,对出口压力或等熵功进行相位平移[27-28]。然而,在爆震工作环境下,涡轮参数峰值点与参数变化平缓的时间段在压力波传播速度上存在显著的差异,基于峰值点同相位假设的相位平移难以真实地反映进、出口工质在相位上的对应关系。鉴于涡轮瞬时性能评价的难度,另一种更为简单的方式是仅关注涡轮的时间平均效率
式中:Pac为实际功;Pis为等熵功;τ为涡轮的总扭矩;ω为转速;ṁ取涡轮进口流量;cp和k依据瞬时涡轮进、出口平均温度插值得到瞬时比热和比热比;π*为便于分析选取瞬时总静膨胀比。
为方便起见,本文也采用这种方法计算涡轮周期平均效率。
本文研究的涡轮在1 个爆震周期的平均效率计算结果见表2,为进行对比,同时给出了本涡轮稳态设计点效率计算结果。从表中可见,涡轮爆震工作状态的周期平均效率严重低于稳态设计点效率,其原因主要在于爆震涡轮内部存在极大的非定常激波损失和带来的分离损失,并且涡轮在大部分时间内存在很大攻角,严重偏离设计工作状态。

表2 涡轮爆震工作状态平均效率与稳态设计点效率对比
3 爆震涡轮内部流场的时空演化特征
上述分析表明,影响爆震涡轮瞬态性能的最主要因素在于进口参数的剧烈时序变化及爆震波在涡轮通道内的传播与演化过程。本节将结合涡轮内部流场结构,详细分析涡轮导叶与动叶构成的几何结构对爆震波传播与反射的影响,探究爆震波及反射波对于涡轮流场结构及性能参数的影响。
爆震波与涡轮叶片的作用过程如图6 所示,图片灰度代表当地压力梯度大小,反映爆震波和反射波的所在位置。图中第1 行(t=0.306T~0.326T)爆震波进入涡轮通道,到达导叶前缘后,一部分沿导叶通道继续向下游传播,一部分则与导叶前缘接触后反射为左行脱体激波,导致进口段呈现倒流。之后随着高能量流体的逐渐流失,进口段的逆向压力梯度逐渐减弱,并恢复到正向压力梯度,工质再次加速涌入涡轮通道,并形成一道强度较弱的新激波,可见于图中第2行(t=0.362T~0.382T)。新激波的传播过程与原爆震波类似,也包括输运和反射过程,输运速度略低于原爆震。这样的运动激波导致了涡轮进口通流特征呈现正流-倒流-正流-倒流的反复状态,但波动幅值逐渐减弱,直到当前爆震波及反射波耗散,涡轮工作状态重新趋于稳定。

图6 爆震波与涡轮叶片的相互作用
爆震波和反射波在短时间内对导叶附近工质的2 次压缩作功,将导致进口段工质温度升高,爆震波作用下涡轮通道内的温度变化如图7 所示。其中,右行爆震波第1 次作功(t=0.306T~0.316T)对进口温度的影响与给定总温变化规律一致;反射波对进口段工质的第2 次作功(t=0.316T~0.326T)则会进一步使进口温度达到更高峰值,爆震波作用下涡轮进口静温时序变化如图8 所示。此后,在逆压梯度的作用下,高能量流体逐渐排出涡轮通道,进口温度迅速下降,直到后续右行激波的进入,进口温度重新提高。相比之下,后续右行激波(t=0.362T~0.382T)由于强度较弱,对工质作功导致的瞬间温度变化也相对较少,温度峰值也显著低于前一峰值。
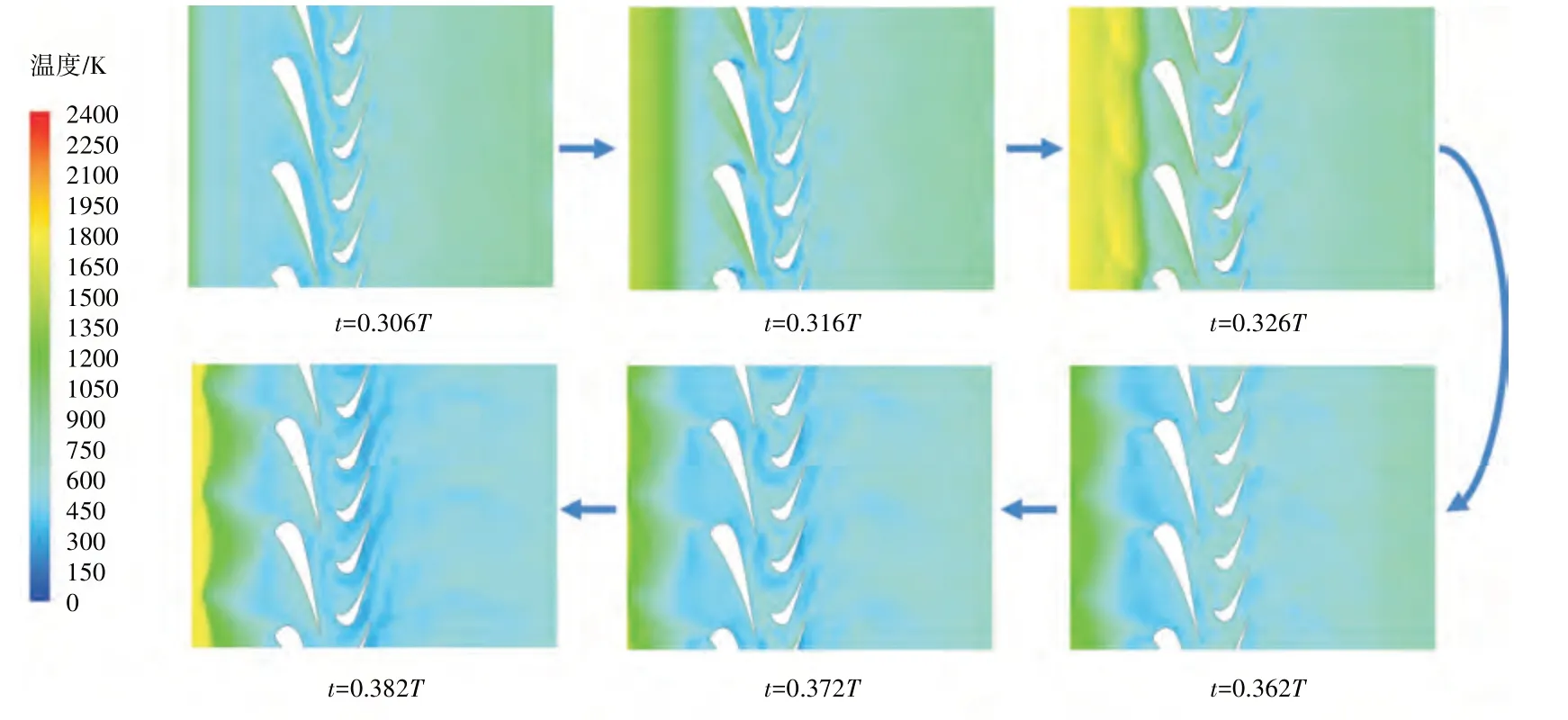
图7 爆震波作用下涡轮通道内的温度变化
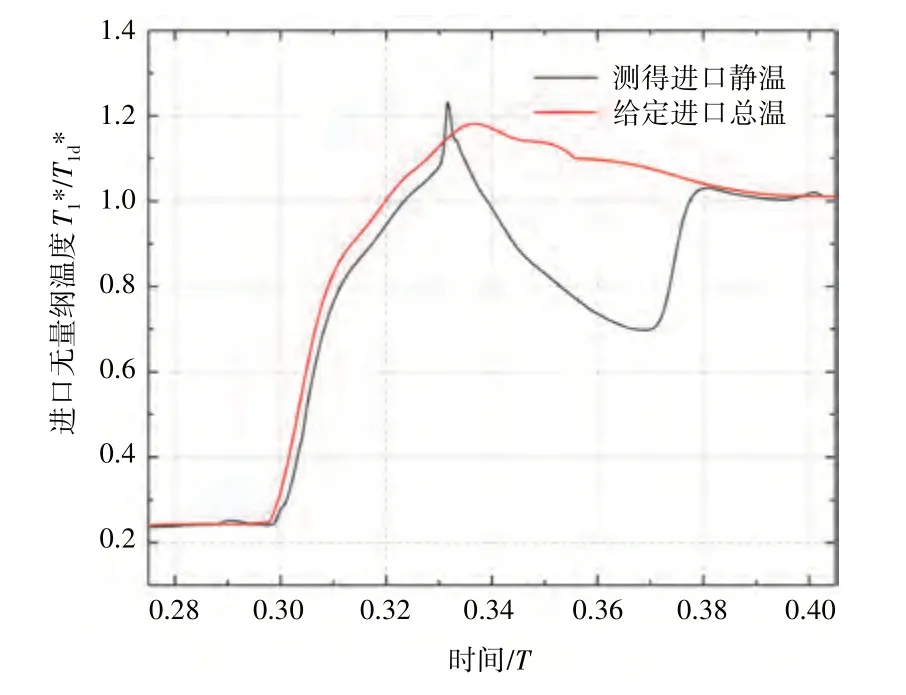
图8 爆震波作用下涡轮进口静温时序变化
爆震波传至转静子叶片排间将在导叶尾缘及动叶前缘附近构成的复杂几何空间内与叶片排产生更复杂的相互作用。在t=0.32T~0.33T的时间段内,爆震波在转静子叶片排间的演化过程如图9 所示。在t=0.32T时刻,爆震波已由导叶尾缘进入转子通道,失去了导叶叶片的限制后,爆震波大部分沿导叶尾缘方向下游输运(红圈部分),少部分由于通道的扩张沿周向向相邻叶片排输运(蓝圈部分)。此后,沿导叶尾缘方向输运的红圈部分爆震波与动叶压力面接触并反射,反射面积占据动叶压力面约80%轴向弦长(t=0.320T~0.326T),随后与周向相邻叶片吸力面最大厚度位置接触,在t=0.33T时刻可观测到马赫反射结构和三叉点T2;而向周向逆时针方向输运的蓝圈部分爆震波则在t=0.32T时刻与相邻动叶接触后分成2 部分,一部分穿过轴向间隙并继续向周向输运(对应t=0.326T时刻靠上蓝圈),另一部分与蓝圈附近的动叶前缘接触(对应t=0.326T时刻靠下蓝圈)。2蓝圈爆震波分别与周向相邻动叶接触后相交干涉,在t=0.33T时刻可观测到2道蓝圈激波的马赫反射结构和上下2个三叉点T1u和T2u。爆震波在叶片排之间的相互作用导致涡轮动叶攻角的剧烈变化(图5),并在约t=0.33T时刻达到最大正攻角。

图9 爆震波在涡轮转静子叶片排间的演化过程
4 爆震涡轮叶片气动及热负荷时序演化规律与机制
在爆震波的冲击下,涡轮叶片受到显著的非定常气动力作用。爆震涡轮叶片排轴向力与周向气动负荷的时序变化如图10 所示,图中的Fd为对应叶片排的稳态设计点气动力。导叶在爆震波直接冲击下,最大瞬时轴向气动力可达涡轮稳态设计点的120 倍以上,最大周向气动负荷为稳态设计点40 倍以上;而下游的转子叶片虽没有受到爆震波的直接冲击,最大瞬时轴向力和周向负荷也为稳态设计点的6~7 倍。如此剧烈的气动力势必会给爆震涡轮叶片包括涡轮盘、轴承等结构的强度和寿命带来极大的挑战。
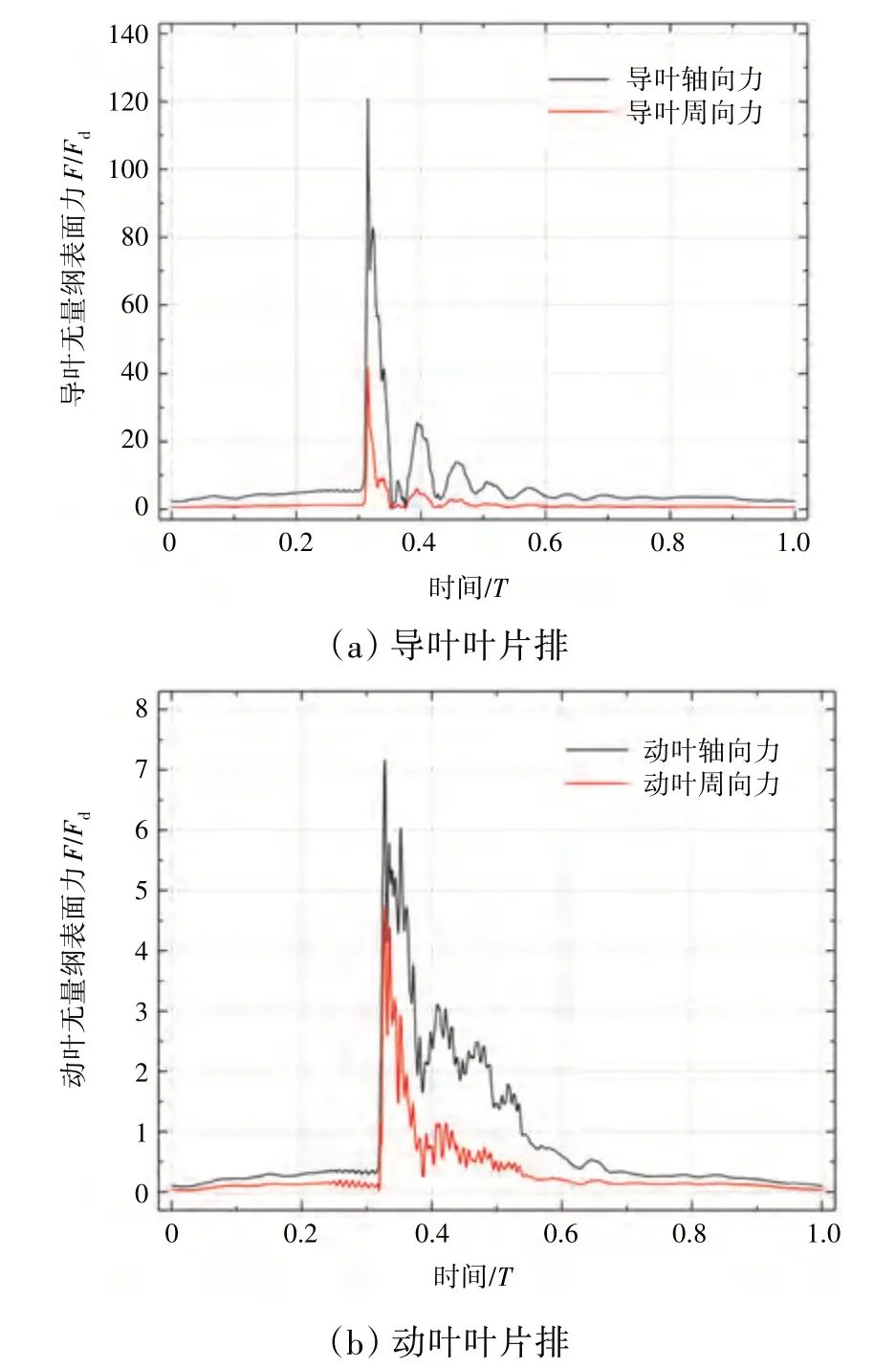
图10 爆震涡轮叶片排轴向力与周向气动负荷的时序变化
需要说明的是,目前的数值仿真已引入涡轮叶型的尺寸模化,在计算叶片排轴向力和周向负荷时,已经引入计算域所包含的1 导叶和2 动叶,可以反映全环的流动结构以及气动负荷的假设。而事实上,轴向相邻叶片排的叶片数量通常是互质的,这使得同一叶片排的不同叶片可能在同一瞬时存在较大的瞬态轴向力和负荷差异。事实上,本文数值模拟分析计算域包含2 个动叶叶片,二者在瞬时的气动轴向力和气动负荷具有很大的差异。t=0.33T时刻爆震涡轮流动结构及动叶负荷分布如图11所示,图中的负荷系数c定义为
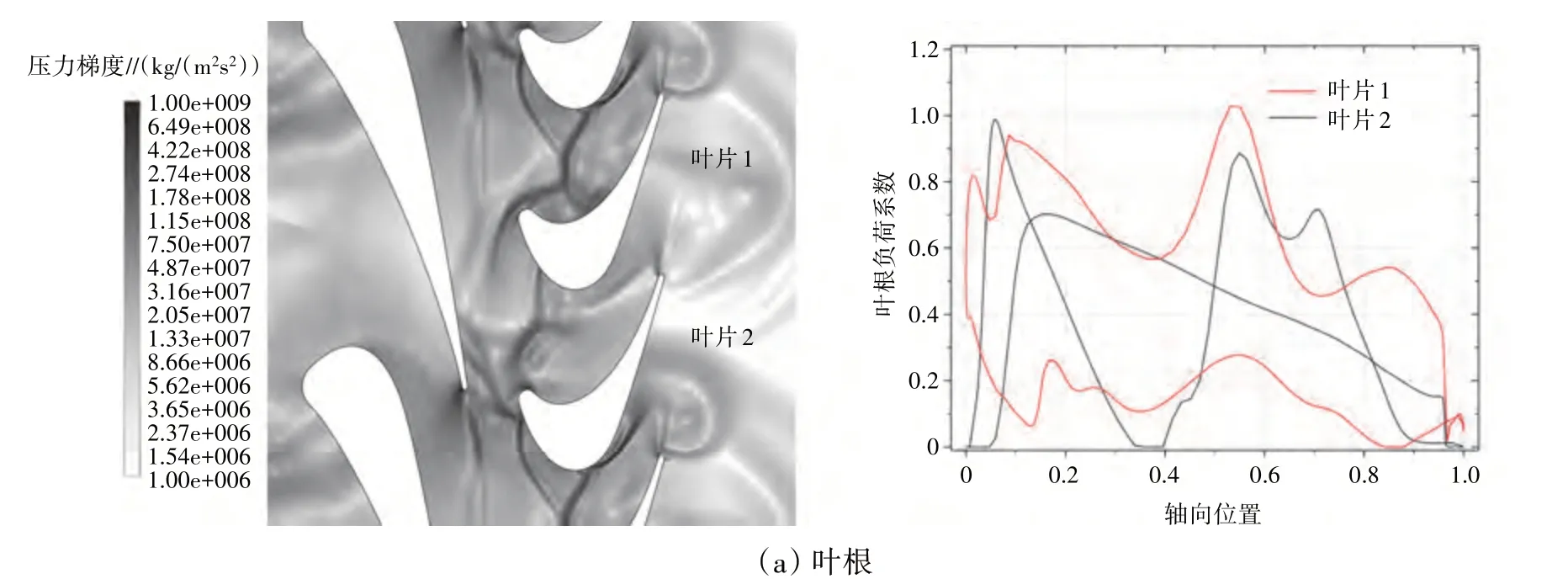
图11 t=0.33T 时刻爆震涡轮流动结构及动叶负荷分布
式中:下标1代表叶片排进口,下标2代表叶片排出口。
从式(3)中可见,爆震波与动叶叶片排的相互作用呈现显著的3 维非定常特征,通过模化涡轮叶型完成仿真,分析叶片瞬态气动力的方法存在局限性,准确的瞬态叶片气动力计算可能需采用全环数值模拟。
上文对涡轮通道温度分布变化规律的分析指出,爆震波和反射波在短时间内对导叶上游工质连续压缩作功将导致进口段的温度急剧升高。事实上,爆震波输运作功还将导致叶表温度的急剧上升,爆震涡轮叶片表面温度的时序变化规律如图12 所示,图中Tv和Tb分别代表导叶和动叶叶片表面附近流体的周期平均温度。导叶叶表流体的最高温度已达到叶表流体周期平均温度的3.5倍(超过3000 K),且在约0.05T的时间跨度内导叶叶表最高温度均超过设计点进口总温,最高温度所在区域的位置主要集中在导叶叶根吸力面最大厚度附近,爆震涡轮叶片表面最高温度所在位置如图13 所示。从图中可见,动叶最高温度略低于导叶,但也达到叶表流体周期平均温度的2.8 倍(超过2200 K),最高温度所在区域位于动叶叶根吸力面最大厚度附近。由此可见,爆震波及其作用下产生的高能量流体使导叶和动叶均面临严重的热冲击,可能产生不同程度的烧蚀。
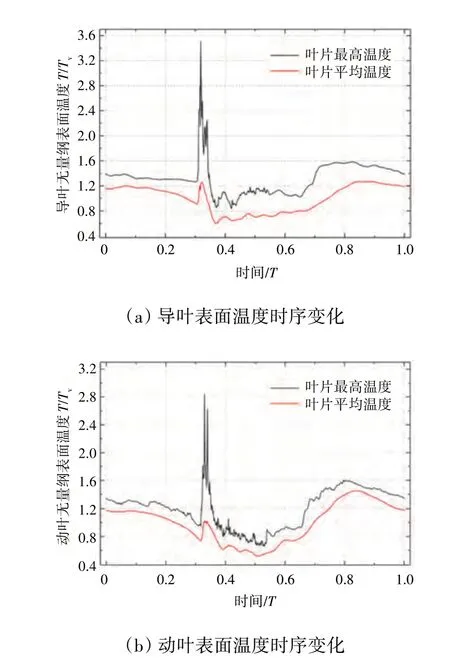
图12 爆震涡轮叶片表面温度的时序变化规律
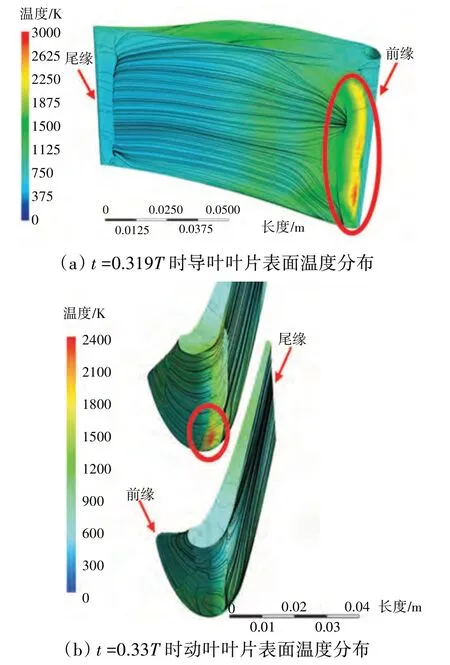
图13 爆震涡轮叶片表面最高温度所在位置
从图12中可见,在受爆震波影响很小的t=0~0.2T以及t=0.8T~1.0T时间段内,涡轮叶片表面的平均温度较高,甚至高于第1道爆震波影响不久的t=0.4T~0.6T时间段,这可能与叶片表面热边界层引起的迟滞效应相关。t=0.10T时刻导叶通道的总温分布如图14所示。
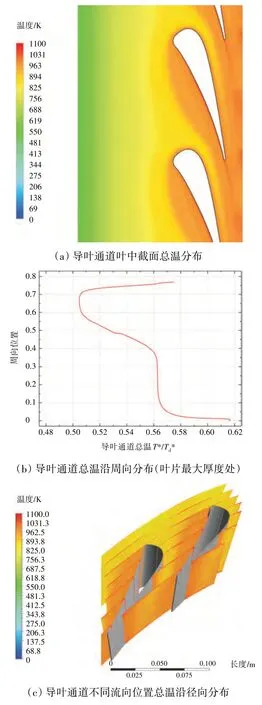
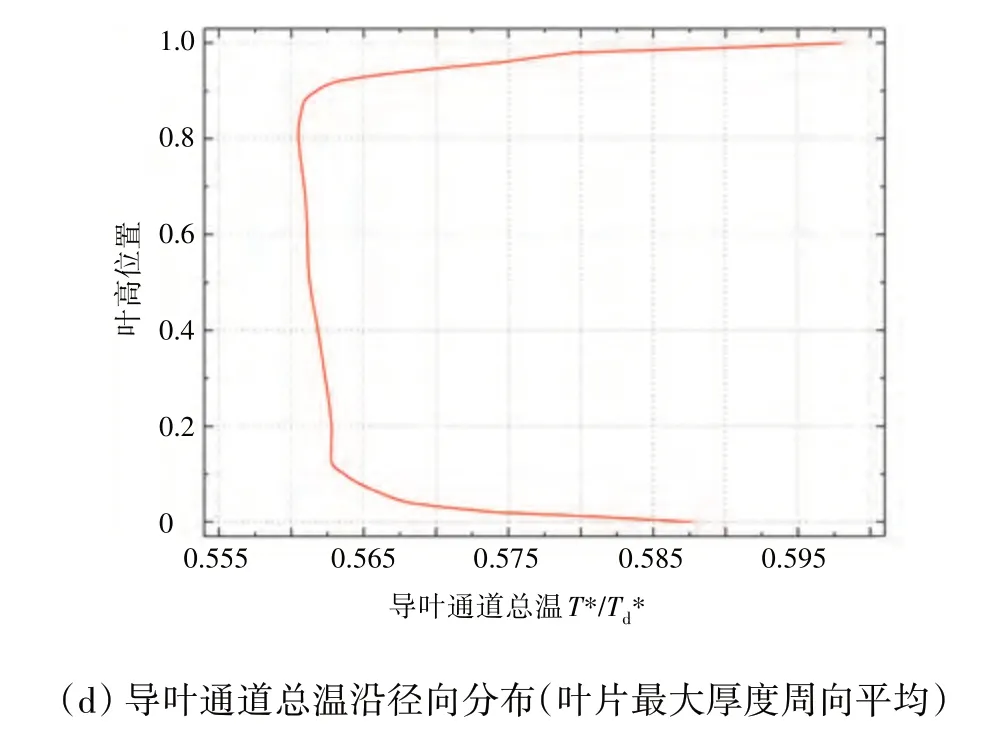
图14 t =0.10T 时刻导叶通道的总温分布
从图14 中可见,叶片、轮毂以及机匣等壁面附近的热边界层会对高能量工质向下游的输运过程造成迟滞,叶表边界层对工质输运的迟滞最明显。由此可见,即使是在爆震波作用的间隙,热边界层的存在仍会显著增加叶片表面的热负荷,从而给冷却和结构强度设计都可能带来严峻挑战。
5 结论
(1)爆震波在导叶进口段的传播和反射会显著影响涡轮的通流能力,导致涡轮进口在正向流动和反向流动间不断反复,流量波动明显。此外,爆震波在传播过程中对工质的压缩作功,使涡轮进口温度升高,而导叶反射波的再次加热使测得的进口温度进一步提高,其值将高于来流温度的峰值。
(2)爆震波与涡轮叶片排间的相互作用导致动叶前缘呈现复杂的激波结构。来流条件的剧烈时变和上述波系结构共同导致涡轮转子进口攻角的变化超过100°,使涡轮的流动损失大幅增加、性能严重降低。
(3)受爆震波的冲击,涡轮导叶排将最高受到超过120 倍设计点的瞬态轴向力,瞬态的周向负荷也超过设计点的40 倍。动叶排承受的最大轴向力和周向负荷约为设计点的6~7倍,且同一叶排各叶片的瞬态气动力可能存在较大差异。
(4)爆震波和反射波对工质的压缩作功导致涡轮叶片表面附近流体温度急剧升高,其瞬态最高温度可达导叶表面流体平均温度的3.5 倍以上,动叶表面流体最高温度也达到动叶表面流体平均温度的2.8倍以上,可能导致叶片表面的烧蚀,也给涡轮冷却和结构强度设计带来极大的挑战。
