基于EFFD参数化的风扇/压气机叶片-端壁一体化伴随优化设计

2023-07-07李伟伟季路成

航空发动机 2023年3期

李鑫，张韬，李伟伟，周玲，季路成

（清华大学航空发动机研究院1，车辆与运载学院2：北京 100084；3.北京动力机械研究所，北京 100024；4.北京理工大学宇航学院，北京 100081）

0 引言

现代先进航空发动机的内部流动非线性程度高[1]、设计参数众多，完全依靠设计师凭经验进行手动设计已难以满足日益提高的发动机性能发展需求[2]。因此，依托计算机和计算技术对以众多参数描述的叶片通道进行精细设计与优化[3]是发展现实与趋势。在计算机优化算法中，全局随机类优化算法与常规梯度类优化算法均无法应对设计参数众多的精细化设计需求。

伴随方法具有计算成本与设计变量数目无关的特性，是最为契合精细化设计概念的合理选择。该方法由Lions 于1971 年首次提出[4]，2000 年由Liu[5]、Dreyer 等[6]用于叶轮机气动外形优化。历经近20 年的发展，伴随优化已成为叶轮机精细化设计与优化的重要工具，在该方法基础上，多点优化[7]、多排叶轮机优化[8-9]、多学科一体化优化[10]、鲁棒性设计[11]及气动不确定性分析[11]等问题均得到了充分研究。在伴随优化系统流程中，参数化方法描述了离散的设计变量取值与连续的外形几何间一一对应的映射关系，因而成为连接流动数值仿真与目标函数梯度分析、梯度寻优的重要桥梁。2017 年Xu 等[12]指出，参数化方法应具有全自动、空间大、无震荡、便于施加几何约束等系统特征。历经近20 年的发展，以扰动控制为主的扰动参数化方法具有更高的设计空间与灵活性，更符合叶轮机精细化设计的需求，也因此被广泛应用，如Hicks-henne 函数、Cst 函数等[13]。作为3 维空间的随机扰动施加方法，自由变形技术（Free-form Deforma⁃tion，Ffd）[14]自2018 年由John 等[15]首次用于叶轮机伴随优化后，便因其设计空间广、3 维连续性强等优势获得研究人员的关注。然而，Ffd 应用过程却无法与叶轮机几何分布特征完全契合。从原理上讲，Ffd 变形过程受限于长方体控制体，难以与圆柱形流道完全匹配，且尽管其能够保证控制体内部实体的曲线连续，于边界位置也难以施加约束，难以保证回转几何的周期性。

2013 年研究团队研发了基于简单H 网格、冻结粘性法、薄层削尖模型的连续型伴随优化系统Opti⁃turbo[16]，经后续不断改进，已具备工程可行的伴随优化应用能力[17]；为解决由网格及湍流模型简化引发的数值精度问题，2017 年进一步研发了叶轮机气动外形离散型伴随优化系统Turbosim_Un[18]，实现了流动数值仿真及伴随敏感性分析精度的显著改进。然而，其仍使用基于Hicks-henne 函数[19-20]的扰动参数化方法，不仅操作复杂，也严重限制了设计空间。为此，从实用的需求出发，顺应行业领域发展趋势，本文以拓展自由变形技术（Extended Free-form Deformation，EFFD）为基础开发了具有叶片-端壁协调控制能力的全新参数化方法，并对跨声速压气机转子Rotor 67 进行优化，在验证TurboSim_Un 优化能力的同时保证参数化方法的有效性。

1 基于拓展自由变形技术的参数化方法

拓展自由变形技术是Coquillart[21]于1900 年对FFD 方法的改进拓展，其主要改进在于对长方体控制体进行变形以构造任意形状控制体，并结合局部变形概念改善控制体边界附近曲线的连续性。文献[20]已对EFFD 理论进行了详细描述，本文仅以Rotor 67转子通道为例展示其实施过程：

（1）以通道形状为控制体，绘制均匀分布的控制点。与流域空间不对等的长方体控制体是FFD 技术无法实现叶片-端壁一体化设计的主要限制，而EFFD 方法中通过控制体变形可构造任意形状控制体。为此，直接以通道流域为控制体进行变形处理，并均匀分布控制体内部控制点，如图1（A）所示。

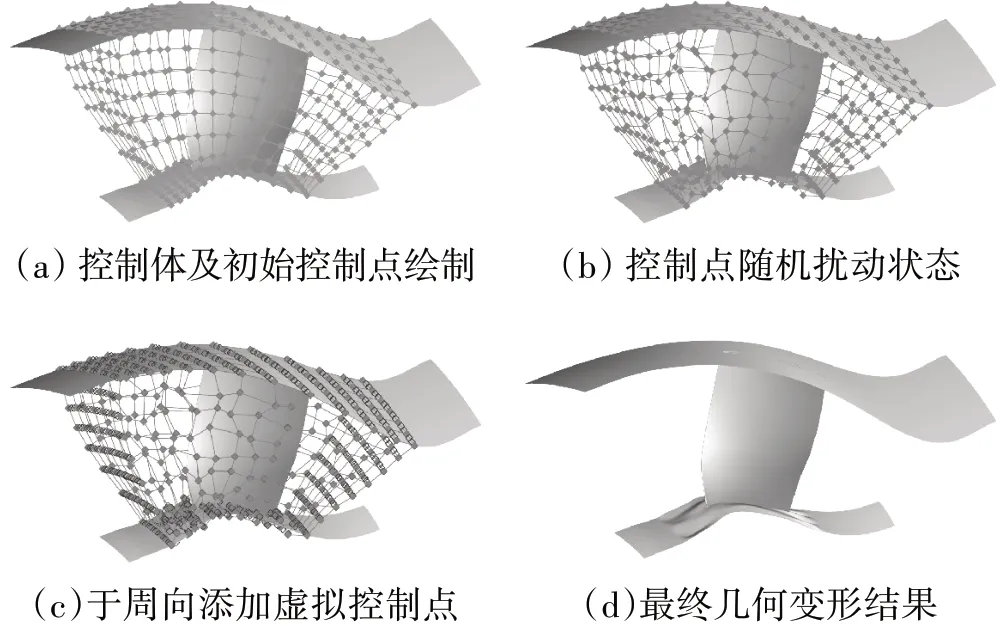
图1 拓展自由变形过程

（2）对于任意实体位置，应用局部变形理念确定其所在的局部控制体位置。为解决控制体边界附近的曲线变形连续性等问题，EFFD 方法需使用局部变形，即仅实体位置附近的控制点干扰方能改变实体位置。局部控制体位置计算需利用Bezier 超曲面性质，以判断包含该实体位置的具体子控制体微元。

（3）对控制点施加扰动，实现实体变形。施加某随机扰动后的边界控制点位置如图1（B）所示。

（4）自动计算局部控制体内虚拟控制点位置。为保证不同子控制体间曲线变形的斜率连续，应在子控制体内施加虚拟控制点，其不参与参数化变形，而根据真实控制点的变化自动调整位置，如图1（C）所示。

（5）使用牛顿迭代，计算实体位置在局部控制体内的相对坐标。

（6）对子控制体进行FFD 变形，计算公式见文献[14]，最终变形结果如图1（d）所示。

2 优化案例

2.1 流动数值仿真介绍

Rotor 67 转子叶片是20 世纪70 年代由美国Nasa设计的低展弦比跨声速风扇/压气机转子叶片，1980年Anthony 等使用激光测速等方法获得了其详细的内部流场数据[22]，包括特性线、截面马赫数云图及流向速度分布等，该转子叶片已成为叶轮机领域广为应用的Cfd 数值校验、流动机理分析和优化设计的典型案例。Rotor 67转子部分设计及试验参数见表1。

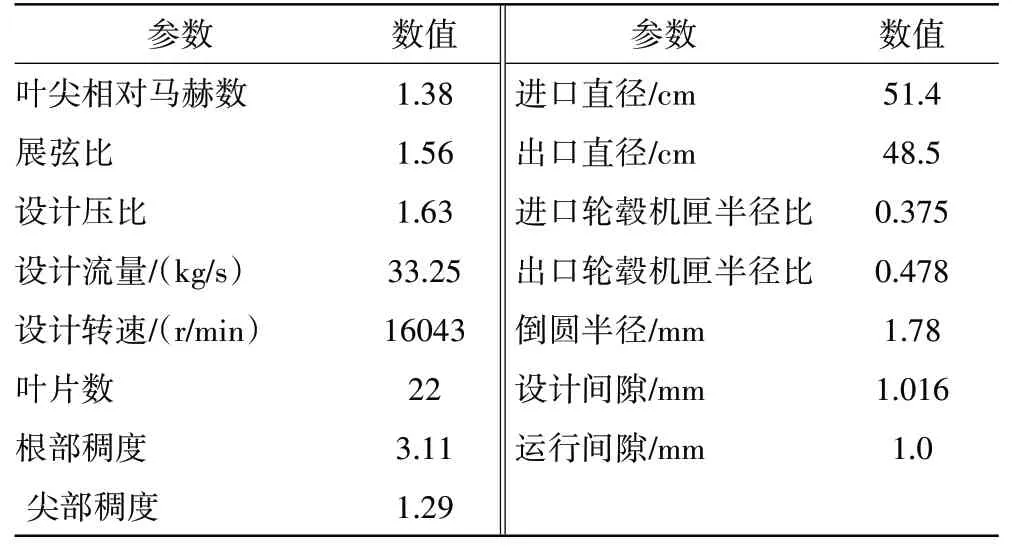
表1 Rotor 67转子部分设计及试验参数

优化过程Rotor 67 转子计算流域进口与叶根前缘的距离为0.10 M，流域出口与叶根尾缘的距离为0.12 M，子午面如图2 所示。采用Autogrid 5 绘制网格，基于Sa(Spalart And Allmaras)模型的网格无关性校验结果如图3所示。

图2 Rotor 67子午面

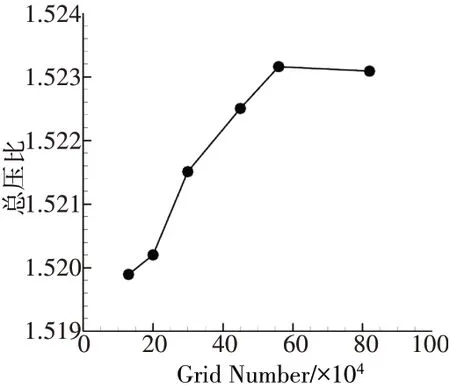
图3 网格无关性校验

经过选择，后续Rotor 67转子优化计算使用58万网格方案，其壁面y+值如图4 所示，基于此网格的Ro⁃tor 67 转子特性线如图5 所示，其中下标choke 表示堵塞流量，本文后续堵塞流量均以图5为基准。

图5 Rotor 67转子特性线

2.2 优化设置

优化过程以效率为目标函数，并采用罚函数法对流量及压比进行约束

式中：η为绝热效率；ω1为流量约束权值，取值约为1000；ω2为压比约束权值，取值为200；M为流量；Pr为总压比；下标0表示原型的参数。

在采用EFFD 参数化方法的优化过程中，轴向控制点数为10，周向控制点数为7，径向控制点数为8，除保证曲线连续型的若干位置控制点、排除叶尖复杂流动干扰的尖部控制点不变外，总变形控制点数为462，总设计参数的数量为1386。

3 结果与分析

3.1 优化进程

在上述设置下，本文Rotor 67 转子伴随优化过程中相关参数变化如图6所示。

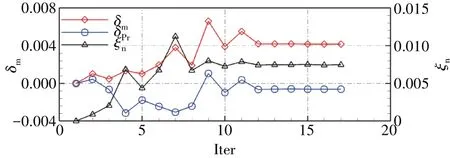
图6 优化过程中性能参数变化

图中，横轴ITER 表示优化后所获得的几何模型次序编号，左纵轴为流量相对偏差δm及总压比相对偏差δpr，右纵轴为效率绝对偏差ζη

由此可知，经16 次伴随优化，Rotor 67 转子效率提升了0.74%，而流量及总压比偏差较小，分别为0.42%及0.11%。

3.2 优化结果性能变化

为检验优化前后Rotor 67 转子的整体性能，分别展示了原型及优化后结果在70%、90%及100%转速下的特性线分布，优化前后特性线变化如图7 所示。从图中可见，本次伴随优化已实现转子气动性能的显著改进，并未发生工况漂移问题，且100%转速状态由于近峰值效率点的工况约束程度较高，堵塞流量仅增大约0.24%，而总压比特性线与原型的仍保持较高的吻合度。具体而言，在100%转速下转子等熵效率提升达到近0.8%；此外，在90%和70%转速下的变工况特性中，峰值效率及近堵塞工况的效率指标同样有所提升，且随着转速的降低，流量及压比偏差减小，但效率提升也减小。

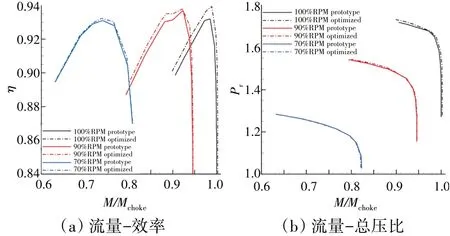
图7 优化前后特性线变化

3.3 优化结果几何分析

为描述伴随优化前后Rotor 67 转子叶片发生的几何变动，展示了若干展向位置的叶型截面，如图8 所示。从图中可见，叶片变形集中在前缘及前缘吸力面附近，而叶片后方变形极小，确保在多排一体化应用时优化结果不会对下游工况产生过大干扰。具体而言，前缘均向压力面侧偏转，且往往伴随着前缘厚度的显著减小，越靠近根部则绝对叶片厚度减小越明显。

图8 叶型变化

厚度是保证优化结果结构强度的重要指标，则进一步提取了相应展向位置的叶片厚度及中弧线弯角分布，如图9 所示。从图中可见，最大厚度位置前的叶片厚度减小是各截面叶型的共同变化特征，但最大厚度及其位置仍与原型的保持较高的吻合度，基本保证结构强度不会大幅降低；另一方面，中弧线在保持弯角分布规律一致的前提下，在前缘后方局部区域内弯角减小而后整体增大，且随展高的增大变化更为明显。

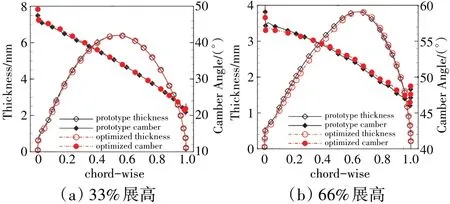
图9 叶型厚度与弯角分布

优化结果叶表变形量如图10 所示，更形象地展示了叶片变化位置。从图中可见，尽管叶根附近变形量绝对值更大，但考虑轮毂径向变化的参与，其叶型变化并不十分明显（图8）；除叶尖几何未参与气动优化外，80%展高附近叶片变化最为剧烈，且变化以前缘后方位置为主；尾缘附近变形均整体偏小，与图8变化对应。

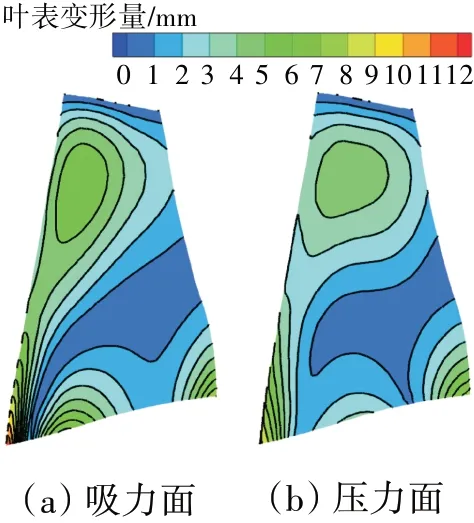
图10 优化结果叶表变形量分布

从图10 中还可见，叶根附近较大的变形量表明轮毂已发生显著改变，作为叶片-端壁一体化优化的另一主要调节对象，轮毂面的径向变化如图11 所示。从图中可见，经伴随优化，轮毂面具有典型“波浪形”分布特征：在前缘前、尾缘前叶表两侧存在3 组较为明显的通道下压区，而在吸力面前缘附近、尾缘前通道中部则明显上抬；整体而言，通道变形形式较为复杂，在任意轴向位置处轮毂壁面型线不再保持等径或单调分布，S3截面部分叶片及轮毂形状如图12所示。

图11 模型6轮毂面变形量

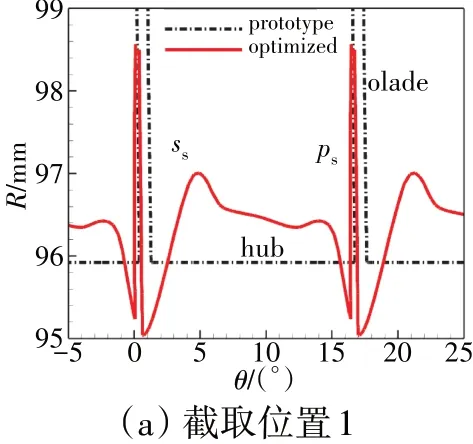
图12 S3截面部分叶片及轮毂形状

图中，SS表示吸力面，PS表示压力面。从图中可见，经伴随优化，除前缘附近外，叶片中后部区域内原本近乎90°的叶片及端壁夹角转化为钝角，且尤以吸力面角区更为明显；此外，端壁曲线呈现典型的“下压-上抬-下压”变化：吸力面及端壁交汇区域以二面角变化为主，通道中部轮毂上抬形成尖峰，而在压力面与轮毂一体化区域并未显著改变二面角，整体表现为平移下沉。

3.4 优化结果流动分析

为判断流动性能提升的内在机理，提取了100%转速峰值效率点位置的出口截面内若干参数展向分布，如图13所示。其中，各相对高度下绝热效率为

图13 出口截面若干气动性能参数展向分布

式中：Pt为总压；Tt为总温；γ为比热比；下标in表示进口，out表示出口。

经伴随优化，近乎在全展范围内效率指标均显著提升，而60%展高以下区域总压均显著提高，在压比约束下尖部总压略有降低。

以20%及80%展高为例，从S1截面的视角展示了优化前后流动的变化，如图14 所示。从图中可见，尽管20%展高尚未形成激波结构，但吸力面加速、尾迹均是流道内主要流动现象。在叶根附近，经伴随优化，前缘吸力面侧高速区范围明显缩减，并结合叶片前半段的厚度调整，吸力面加速区范围同样显著减小；在流速变化影响下，尾迹范围明显减小，表征尾迹损失显著改善。而在80%展高截面内尽管尾迹、激波结构变化并不明显，但借助厚度调整，激波前高马赫数的范围和数值均略有减小，同样表征激波损失的改善。

图14 若干展向位置相对马赫数分布

优化前后叶表吸力面静压分布如图15 所示。从图中可见，优化结果的低压区范围明显缩减，对应叶表高等熵马赫数区域减小，与前述结论一致。

图15 优化前后叶表静压分布

角区和轮毂形状的变化及端区附近流动性能的显著提升，表明轮毂附近流动已大幅改善，为此，展示了图12中截取位置2的周向S3截面马赫数分布，如图16 所示。从图中可见，相较于原型，优化结果的主流区流速变化较小，而端区流速略有提高；以相同的速度等值线与端壁型线间相对面积作为衡量附面层损失的近似判据判断其符合二面角原理，增大的二面角分布对改善角区附面层交汇损失具有正向增益作用。

图16 截取位置2的S3截面相对马赫数分布

优化结果的轮毂面型线具有典型的“下压-上抬-下压”分布特征，其中部上抬的轮毂可有效抑制角区横向二次流传播，进而改善吸力面分离涡结构，吸力面侧尾缘附近的壁面极限流线如图17 所示。从图中可见，经伴随优化，尾缘后方的涡结构甚至基本消失，吸力面后方的涡尺寸同样略有减小，表明端区性能有极大改善。优化前后通道出口截面的总压分布如图18 所示。从图中可见，根部区域的低总压区范围明显减小，再次表明根部区域流动性能显著改善。

图17 吸力面侧尾缘附近的壁面极限流线

图18 优化前后通道出口截面总压分布

然而，考虑壁面极限流线（图17）为基于SA 湍流模型的计算结果，其在复杂湍流状态下往往误差较大。为此，以CFX 商业软件为工具，使用剪切应力输运（Shear Stress Transport, SST）湍流模型在相同边界条件下对原型及优化结果进行气动仿真，并提取其相应位置的流线分布，分离涡结构计算结果如图19所示。从图中可见，经伴随优化，尾缘后方涡结构获得了极大改善，整体表现为展向尺寸及轴向范围大幅缩减。