基于微分熵与深度残差网络的脑电信号情感识别

杜秀丽 马振倩 郭庆汝 邱少明 吕亚娜

(大连大学通信和网络重点实验室 辽宁 大连 116622) (大连大学信息工程学院 辽宁 大连 116622)

0 引 言

人类的情感既包含人类对所处外界环境或者自身心理活动而引发的生理反应,还包含这些生理反应而触发的心理反应,可以概括为一种整合了人类的行为、感觉、思维的状态活动[1]。人的情感是人与人交往的一个重要因素,对一个自然的人机交互界面来说,识别、解释和响应语音中表达的情感史至关重要的[2]。在人-机交互系统中,如果能够准确并且快速地识别出体验者的情感变化,智能设备可以以此作为依据进行相应的调整,使得在使用过程更加满足使用者的生理与心理需求[3];在军事领域运用情感识别,能够辅助指挥人员依据战士的情感状态制定相应合适的作战计划。所以,对人的情感状态进行准确而有效的评估与识别,已经成为各个研究领域的重点话题[4]。

脑电信号(Electroencephalogram,EEG)因具有不可伪装性、实时差异性和容易采集等优点逐步成为研究情感识别的生理依据。Duan等[5]利用能量频谱特征对积极与消极情感进行二分类,分类准确率为76.56%。柳长源等[6]通过左、右侧导联的微分熵特征,提取脑电信号的不对称性特征,结合支持向量机对情感分类识别,平均准确率为88.625%。Murugappan等[7]提取EEG信号熵特征,比较了六种情绪状态,如恐惧、高兴、惊奇等,发现利用脑电熵特征分类的最大平均准确率为83.04%,表明脑电熵特征可以有效地区分不同情感状态。Chai等[8]提取脑电信号的六种时域统计特征,利用卷积神经网络识别愤怒、惊奇和悲伤等情感,识别准确率最高可达95%。Zheng等[9]利用挑选的8个电极:AF3、AF4、F3、F4、F7、F8、T7和T8,得到了87.5%的情感识别效果。田莉莉等[10]将截取的62导联的脑电信号数据结合改进的卷积神经网络实现脑电情感状态的识别,达到94.7%的准确率。张家瑞等[11]采用多频带与多通道的EEG信号情感识别方法提取EEG信号的微分熵特征实现情感状态识别,总体准确率为91.99%。总结以上分析方法可以发现:现有的脑电信号情感识别方法大都是挑选出与EEG信号情感变化相关度较大的某几个单导联进行特征提取与特征选择,往往会忽略掉其他导联EEG信号的信息以及导联间隐匿存在的空间拓扑结构特征,而这些信息和特征往往对情感状态的识别具有关键性作用。

本文提出基于微分熵特征(Differential Entropy,DE)[12]和深度残差网络(Deep Residual Network,ResNet)[13]相结合的脑电信号情感识别方法。在对原始EEG信号进行分频带后,采用微分熵来衡量每个导联在特定时间间隔的特征,将各个导联的特征组织映射到二维平面中,作为深度残差网络的输入,进行脑电信号特征自动提取、学习和分类,以提高EEG信号情感识别的准确率。

1 全导联脑电信号微分熵特征

传统的脑电信号情感识别过程中往往是挑选某几个导联进行特征提取,实现特征识别的目的。现存的方法没有利用其他导联采集的信息,也会忽略掉导联间存在的整体空间拓扑结构特征,这些隐匿的特征往往对提高情感识别的准确率发挥着举足轻重的作用。针对以上问题,本文提出基于微分熵特征的全导联脑电信号特征表示方法。对情感EEG信号利用短时傅里叶变换,分别将EEG信号的全频段、γ段、β段和α段的微分熵特征映射到二维平面,得到情感脑电信号的二维特征表示。

1.1 脑电信号短时傅里叶变换与微分熵特征

EEG信号是最常见的非平稳、随机信号,如果仅仅从时域或者频域上进行特征分析,很难达到我们所期待的目的。信号的时频分析往往相对于时域和频域分析更能随着时间的变化反映出频域的变化特征。短时傅里叶变换就是种常用的时频分析工具,因具备简捷有效的优点,被广泛应用。

假设研究的原始信号为x(n),选取的窗函数为d(n),利用式(1)可以得到脑电信号的短时傅里叶变换,本文在实际操作中选择汉宁窗作为窗函数(汉宁窗不但能够得到EEG信号随时间变量的频谱变化,还能有效减少频谱能量泄露):

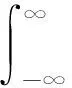
(1)

对于微分熵的定义如下:

(2)

式中:f(x)表示时间序列的概率密度函数。满足高斯分布特性的连续时间信号微分熵计算公式如下[13]:

(3)

根据上述公式可以清晰地发现:满足高斯分布的时间序列信号的微分熵只与方差相关。对于一段已经经过归一化处理的EEG信号XN(N表示脑电信号的长度),可以得到其方差表示如下:

(4)

EEG信号的方差可以由能量谱P的均值表示,得:

(5)

通过上述的叙述,EEG信号某个频带的DE可以由此频带能量谱的对数近似表示。

1.2 脑电信号微分熵二维特征映射

为了尽可能多地挖掘到所有导联间隐匿空间拓扑结构特征,将截取的62通道的脑电信号分别提取得到信号的全频段、γ段(31～50 Hz)、β段(14～31 Hz)和α段(8～14 Hz)的微分熵映射到二维平面,具体的映射排列方式如图1所示(没有放置电极的部位进行置零处理)。图1中左侧为脑电信号采集时62路电极放置方式,右侧分别表示全频段、γ段、β段和α段的62导联微分熵特征,以此作为深度残差网络的输入,实现全导联信息及空间拓扑结构特征的自动挖掘和学习,建立EEG情感分类模型。

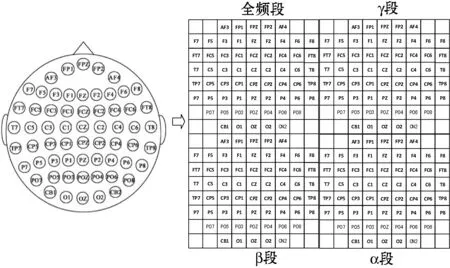
图1 EEG信号微分熵二维特征映射展示

2 本文方法

2.1 框 架

卷积神经网络(Convolution Neural Network,CNN)是一种非常高效的深层前馈神经网络,其网络结构对平移、比例缩放、倾斜或其他形式的变形具有高度不变性。典型的CNN结构由输入层、卷积层、池化层、全连接层、输出层组成。

对于深度神经网络,普遍认为加深网络层次是增强非线性拟合能力、提高模型识别准确率的有效手段。但随着网络层次的增加,会伴随出现梯度消失和梯度爆炸的问题。为了解决深度卷积神经网络因网络层数加深而引发的退化现象,He等[13]提出了深度残差网络的模型结构,解决了深层网络面临的收敛难、调优难等问题,克服了传统卷积网络随着网络层数增加而导致的退化问题。

为自动挖掘各个导联信息及导联间空间拓扑结构特征,本文提出的基于微分熵特征与深度残差网络的脑电信号情感识别方法整体流程如图2所示。对预处理后的情感脑电信号按照不同的频带提取微分熵特征,并将全频段、γ段、β段和α段的微分熵特征映射到二维平面,得到情感脑电信号的二维特征表示;进一步地将EEG信号的二维特征微分熵特征作为深度残差网络的输入,实现多导联间隐匿空间拓扑结构特征的自动提取和学习,建立EEG情感分类模型。

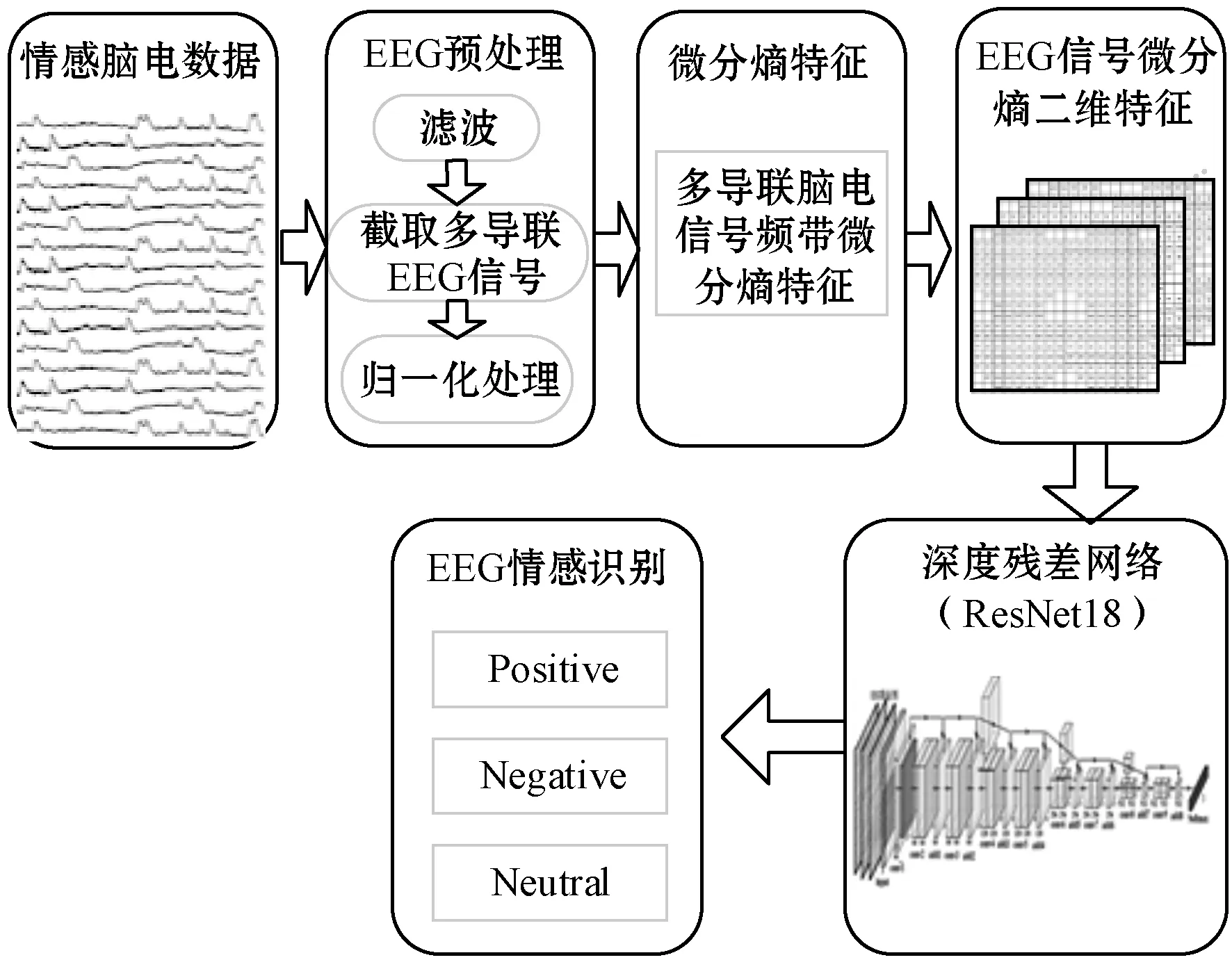
图2 基于微分熵特征与深度残差网络相结合的脑电信号情感识别总体框架

2.2 脑电信号情感识别的深度残差网络设计

62导联的情感脑电信号经过预处理、短时傅里叶变换后得到全频带、γ段、β段和α段的微分熵特征,将提取到的特征按照图1的排列方式转化为二维特征。由于图像的像素较小,并且数据较为“集中”,所以本文将原始图像利用“双立方插值算法”[14]放大到224×224×1的像素,以此作为深度残差网络的输入。表1为设计的网络结构参数,图3为结构,本文针对EEG情感状态这个数据集,采用ResNet18网络模型进行分析,并通过Softmax函数得到情感识别的结果。

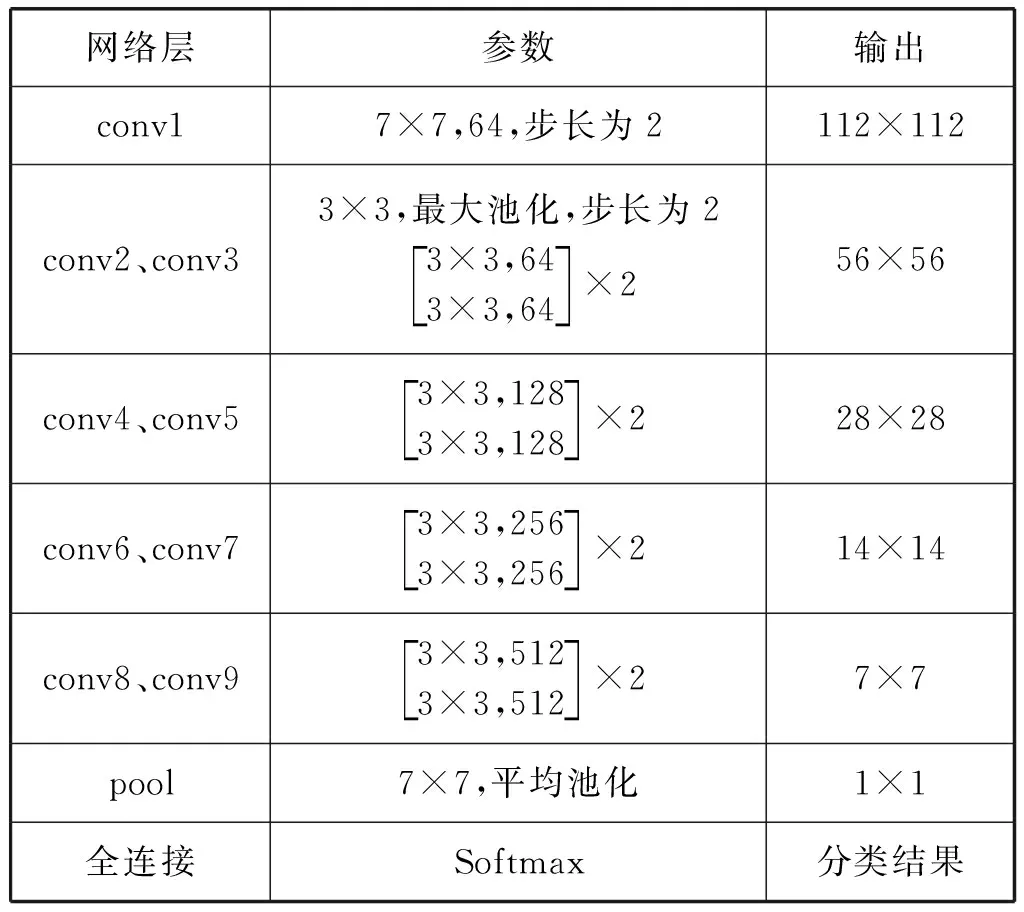
表1 ResNet18超参数

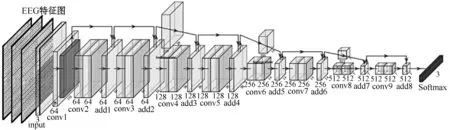
图3 本文设计的ResNet18结构

3 实验与结果分析

3.1 实验数据

本文采用国际公认的人类脑电情感数据集SEED作为实验数据[3]。该数据集使用电影片段作为情感诱发素材,情感状态分为3类:积极、消极和中性。

EEG基本频段如图4所示,对EEG信号数据预处理,截取的脑电数据长度为800,样本总量为10 860。EEG信号经过归一化处理后,得到EEG信号微分熵二维特征映射图。

3.2 仿真及实验结果分析

实验采用的硬件设备为Intel Core 4.20 GHz i7-7700 K CPU和NVIDA Geforce GTX 1080 Ti GPU。软件环境采用MATLAB2014a和PyCharm 2019,同时借助Keras框架实现改进的ResNet18网络,采用自适应动量估计(Adaptive Moment Estimation,Adam)优化算法,分别设置参数为:循环迭代次数100次,初始化学习率为0.001。

本文采用下列四个定量模型评估指标对模型的性能进行评估:准确率(Accuracy)、精确率(Precision)、召回率(Recall)与综合调和分数指标(F1)。评估指标定义如下:

(6)

(7)

(8)

(9)

式中:TP表示被模型分类正确的正样本;FP表示被模型分类错误的负样本;TN表示被模型分类正确的负样本;FN表示被模型分类错误的正样本。

对于N分类问题的综合调和分数指标为:

(10)

3.2.1 基于全导联脑电信号微分熵识别结果

为了验证本文方法的优越性,同样提取了相同时间段内情感脑电数据的功率谱密度、近似熵特征,按照以上方法得到相应的二维特征映射图开展对照实验。表2分别给出了利用功率谱密度(PSD)、近似熵(ApEn)[15-16]和本文的微分熵(DE)特征进行脑电信号情感识别的每折实验测试集准确率、五折实验的平均准确率、标准差。

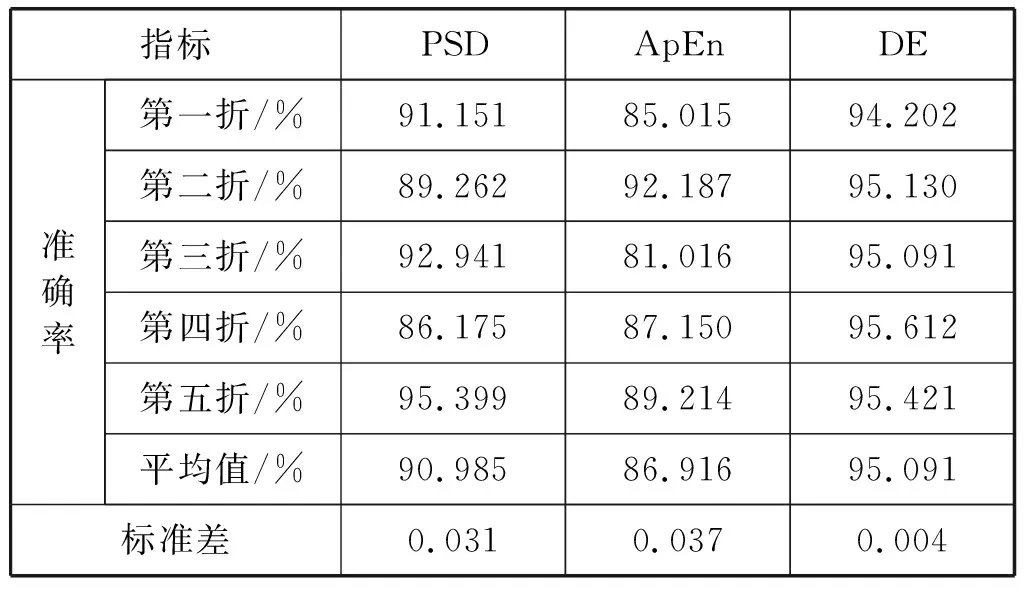
表2 不同EEG信号特征每折实验测试集准确率、五折实验的平均准确率、标准差

分析表2可以得出:应用功率谱密度、近似熵和本文的微分熵特征识别的平均准确率分别达到了90.985%、86.916%和95.091%。脑电信号的三种特征分别结合本文方法进行情感识别都得到了比较令人满意的准确率,说明本文将全部导联脑电信号作为统一整体,利用深度残差网络自动地挖掘全导联信息及导联间隐匿的整体空间拓扑结构特征进行情感识别的方法是十分有效的。

每折实验对应的分类混淆矩阵如表3所示。为了更全面地对模型性能进行评估,采用精准率、召回率和均值作为评级指标,结果如表4所示。可以看出,每折实验的精准率与召回率之间都相差大约0.02,并且两个指标普遍保持在0.92以上,整体在0.92～0.97之间,体现出本文模型具有很强的泛化能力。对于综合指标Macro而言,模型每折实验的值均在0.940以上,说明在Precision与Recall一样重要的情况下,本文方法达到了较为理想的结果。

表3 微分熵特征混淆矩阵

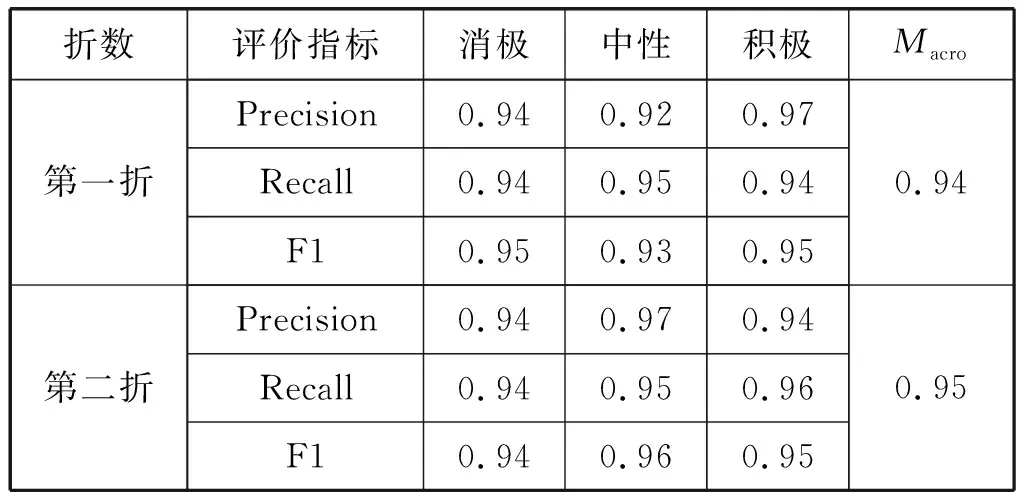
表4 微分熵特征分类指标

3.2.2 同类研究对比

为了进一步验证基于本文方法的脑电情感识别效果的科学性与优越性,将本文方法与采用相同数据集的其他识别方法进行比较。Li等[17]将提取到的不同导联脑电信号的微分熵映射为二维形式,以此作为分层卷积神经网络的输入,识别准确率为88.20%,同时发现Beta波和Gamma波对情感识别起着关键作用。Zheng等[3]提取脑电信号的微分熵特征进行特征平滑、降维,将得到的低维特征结合判别图正则极限学习机进行情感识别,准确率为91.07%。田莉莉等[10]采用一维卷积神经网络随机森林情感识别的方法对62导联的脑电数据进行自动特征提取,识别准确度达到94.7%。对比发现,本文基于微分熵特征与深度残差网络的脑电信号情感识别方法在相同数据集上充分挖掘了各个导联信息及导联间隐匿的空间拓扑结构特征,该方法的识别平均准确率为95.10%。

4 结 语

本文针对现有EEG信号情感识别中没有考虑到导联间存在的整体空间拓扑结构问题,提出基于微分熵与深度残差网络的识别方法。首先,将全部导联脑电信号作为一个整体,把EEG信号各个频带的微分熵特征按照相应的电极空间位置、频段顺序映射为EEG信号微分熵二维特征;然后,利用深度残差网络实现二维特征的自动提取,以充分挖掘了各个导联信息,及导联间EEG信号中隐匿的空间拓扑结构特征,进而提高脑电信号情感识别的准确率。

为了验证本文方法的性能,分别提取了相同时间段内各导联EEG信号的功率谱密度、近似熵和微分熵特征得到二维映射特征图,以此作为深度残差网络的输入。实验结果表明:脑电信号的三种特征分别结合本文设计的网络进行情感识别都得到了比较令人满意的准确率,说明本文将全部导联脑电信号作为统一整体,利用深度残差网络自动地挖掘导联间隐匿的整体空间拓扑结构特征进行情感识别的方法是十分有效的;进一步对比三种特征结合本文方法的准确率可知,微分熵的平均识别准确率最高,功率谱特征次之,近似熵特征最低,说明微分熵特征更适合表示脑电信号。与其他识别方法进行比较可知,本文基于微分熵特征与深度残差网络的脑电信号情感识别方法在相同数据集上充分挖掘了各个导联信息及导联间隐匿的空间拓扑结构特征,识别平均准确率为95.10%,进一步表明了本文方法的优越性。