基于DPI-C的脉动阵列模块验证平台
2023-07-06王鑫,陈博
王 鑫,陈 博
(江南大学 物联网工程学院,江苏 无锡 214122)
0 引言
人工智能(AI,artificial intelligence)加速芯片[1]很大一部分的算法涉及到矩阵运算,在矩阵运算过程中,其中的数学算术包括乘法运算,加法运算。矩阵乘法是一种计算量很大的算术运算,它被认为是许多信号处理应用的关键。同时,随着AI加速芯片的巨大进步,边缘计算[2]开始进入人们的视野,边缘设备功能也变得强大,AI向边缘的移动更是一种必然。研发人员在开发AI芯片时需要设计并实现有关AI算法单元,对于AI算法而言主要进行的数学运算是卷积操作。在硬件上经常使用到的卷积硬件结构有加法树、Eyeriss和脉动阵列,其中的脉动阵列就常常应用于AI加速芯片领域之中[3]。
在芯片设计人员设计并实现芯片内部模块时,后续的验证工作也是不可忽略的,设计的模块只有经过了验证人员的全面验证,排查一切可能出错的点并加以改正之后,才可以让它应用于芯片中,否则在后续流片时可能会出现致命的错误,从而导致之前的努力和投入的金钱都付之一炬。对脉动阵列模块进行验证时,其参考模型在整个验证平台的实现中较为繁琐和耗时,主要原因出现在浮点数乘加运算。为了解决这一问题并鉴于C/C++等高级语言可以更加方便的实现激励读取、参考模型构建等功能,本文采用C语言来辅助完成参考模型的编写。本文的验证环境使用UVM(universal verification methodology)[4-5]来搭建,利用SystemVerilog的DPI[6-8]技术将C 代码与验证环境连接起来,有效地提高验证效率,实现验证平台的重用。
1 所验脉动阵列结构
脉动阵列(systolic array)的架构是简单的、有规律的、模块化的和并发的,它可以有效计算矩阵-向量相乘或者矩阵-矩阵相乘[9-11],它是一种应用在片上多处理器的体系结构。在这一节中,主要简单列举两个矩阵相乘的具体计算过程从而引出脉动阵列,并介绍本文中所使用脉动阵列的具体结构。
1.1 基本矩阵运算及PE单元
给出两个2×2阶的A矩阵和B矩阵,两矩阵相乘如式(1)所示。C矩阵由A、B矩阵相乘得出,其元素的具体计算过程如式(2)所示:
图1为A、B矩阵相乘得出C矩阵的空间表示法,呈正方体结构。每个节点上执行乘加运算,在脉动阵列的体系结构中这些节点称为处理元素(PEs,processing elements)。在图1中可以看出A矩阵中的元素都是从正面进入,B矩阵的元素是从左侧面进入,C矩阵元素从正方体上方得出。其中A矩阵的单个元素经过一个处理元素运算后,并不会即刻消失,而是继续与走向下一个处理元素,同理B矩阵的元素也是以这种方式进行运动。从图中可以看出,整个矩阵的运算是从正方体的底面开始,在顶面结束,正方体的每一面的每一个横边所表示的是A、B矩阵内的元素,而竖边所表示的是中间运算结果,可以看出底面的4个处理单元经过计算得出结果后,各自把得到的结果发射到上面的处理元素作为被加数。经过这种空间表示法可以形象地解释矩阵相乘其实是以向量的形式进行运算,同时又把向量拆分至元素,从而更加形象地描述了矩阵运算过程。
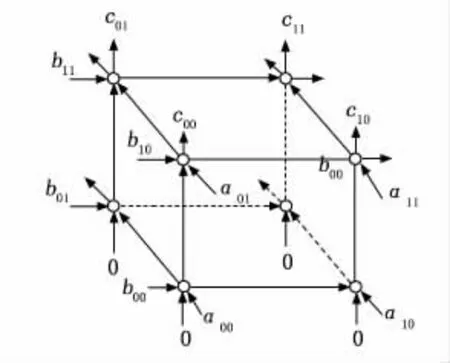
图1 A×B矩阵的空间表示法
A、B矩阵在阵列中的运算方式以及矩阵元素在PE中的运算过程如图2所示。在图2中,左图可以看出A、B矩阵内的元素是以西、北方向进入阵列中进行运算,输出结果在南方;右图是C矩阵中的元素在PE单元中具体运算过程剖析图,其中的椭圆表示一个PE单元。
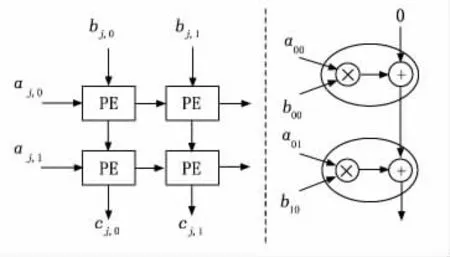
图2 二维阵列和PE单元运算过程
在图2中,B矩阵以列向量的形式送进阵列中,4个元素分布在对应的位置,如图2左图中的左上角是b0,0,右下角是b1,1,A矩阵则以行向量的形式进入阵列与排布好的B矩阵进行运算。我们可以看出A矩阵的行向量进入阵列后,它在未完全涉及所有阵列之前,并不会发生变化,例如a0,0元素在向右游走时,是贯穿两个PE单元后变为无效,这样才能保证A矩阵的行向量与B矩阵的列向量进行运算,A、B矩阵完成了标准的矩阵运算。
1.2 脉动阵列内部结构
脉动阵列是由多个PE单元编排而成。本文中的待测设计(DUT,design under test)是由32×32个PE 单元组成的脉动阵列,其二维空间分布如图3所示,呈正方形结构。此阵列把每列的32个PE单元划分为一个DOT(vector dot product unit),每一个DOT 运算后会产生1个运算结果作为新矩阵的元素。
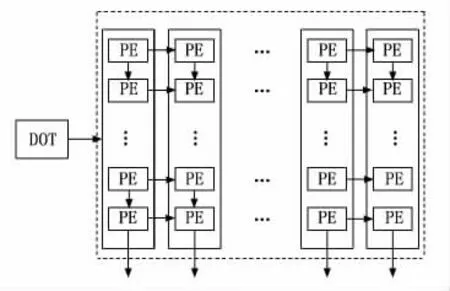
图3 脉动阵列内部结构
划分后的DOT 是执行一次矩阵乘运算中一个矩阵的行向量乘一个矩阵的列向量的运算操作。选择的行向量会不断的向右方向进行延续并与下一个列向量进行运算,即一个行向量需要游历32个DOT 后才会失效,此时下一个行向量便会进入。脉动阵列中参与运算的数都是浮点数,经过脉动阵列运算之后,最终会形成一个由32个浮点数所组成的向量,每经过32 次运算就会组成一个32×32 矩阵。1.3小节详细地描述了矩阵是如何在脉动阵列中进行运算的。
1.3 矩阵送入脉动阵列进行运算
在脉动阵列中,实现32×32矩阵运算分为以下步骤:
1)先将一个n=32的B矩阵分成32个列向量送入脉动阵列中的每一个DOT,等待另一个行向量a的进入,a向量与每一个DOT 进行运算。经过32个DOT 的运算之后可以得到新向量。
2)每产生32次新的a向量并与之前在脉动阵列中排布好的B矩阵相乘,便可以得到C矩阵。
3)在完成一次C矩阵的计算后,开始更换新的B矩阵与新的a向量,这样经过再一次的运算便形成新的C矩阵。
在每个DOT 中,每个PE 单元同时进行乘加运算。每两个相邻的积相加,参与一次加法的积不可以与另一个相邻的数进行相加。得出的和再一次跟另一个和进行相加,逐步重复下去,便形成加法树的形式。其运算过程如图4表示。

图4 单个DOT 结果运算输出过程
2 基于DPI-C的验证方案
验证人员在正常情况下,可以利用SystemVerilog直接完成参考模型的编写,但是在一定情况下,利用C/C++是唯一解决参考模型编写问题的途径。例如,当遇到复杂的函数、SystemVerilog中不存在的、复杂的数据类型时,便可以使用C/C++来辅助完成验证环境的搭建,这样既快捷又高效。对于脉动阵列中的浮点数运算,主要是利用C程序进行建模,之后通过DPI技术把C 代码放进验证平台所需的位置来辅助完成脉动阵列的验证。
2.1 直接编程接口
DPI-C利用了SystemVerilog的直接编程接口连接C 编程语言,实现了SystemVerilog 和C 语言之间的数据通信[12]。一旦声明或者使用了import语言 “导入”了一个子程序,就可以像调用SystemVerilog中的子程序一样去调用它,使用起来非常方便。通过较为高级的编程语言实现复杂模型比使用HDL语言要轻便很多,并且仿真速度也比较快。比如,在C 语言中,它已经提供了很多库函数,直接调用即可,无需重新编写。这样既保证了激励编写的正确性,又提高了可重用性。同时C 语言目标代码的执行速度比HDL仿真速度至少要提高一个数量级。在本文中通过DPI技术实现C代码的更高层次的复用。
在对特殊的DUT 进行验证时,采用直接编程接口也可以很便利地把C 代码与UVM 验证环境连接起来,按照下面4个步骤进行。
1)编写C代码,实现所需算法。在编写C 代码时,需要声明包含头文件svdpi.h,是因为在svdpi.h 中包含了SystemVerilog DPI结构和方法的定义。
2)完成C 与SystemVerilog的通信。在UVM 验证平台中,通过导入函数或者任务的方式来调用C 代码,DPI也允许在C代码中通过导出函数和任务来调用SystemVerilog中的方法。
3)匹配数据类型映射。由于SystemVerilog与C 语言数据类型差异较大,SystemVerilog中定义了通过DPI传递的每个数据类型的匹配模式。需要注意的是,DPI并不会检查数据类型的兼容性,需要使用者自己保证数据匹配的正确性。
4)利用仿真工具编译C程序的方法,生成最终的目标码,并与SystemVerilog混合运行。
2.2 非标准化的浮点数
IEEE二进制浮点数算术标准(IEEE754)是20 世纪80年代以来最广泛使用的浮点数运算标准[13],许多CPU以及浮点运算器都采用了这一标准。一个浮点数的表示方法可以为:
其中:sign为符号位,exponent为指数位,fraction为小数位。对于指数位而言,它实际上是指数的实际值加上某个固定值,这个固定值在IEEE754标准中被称为偏置并规定该值为127,即2e-1-1,e取数字8。这里需要注意的是,IEEE754标准中存在3个特殊值:
1)如果指数位是0,并且小数位为0,那么这个数是±0(和符号位相关)。
2)如果指数位是255(2e-1),并且小数位为0,那么这个数是±∞(和符号位相关)。
3)如果指数位是255(2e-1),并且小数位不为0,那么这个数表示不为一个数(NaN)。
常见的浮点数有:半精度浮点数(16bit)、单精度浮点数(32bit)、双精度浮点数(64bit)。在本文中的脉动阵列所运算的浮点数是半精度浮点数和单精度浮点数,其中单精度浮点数是定制的,即在IEEE754标准的基础上进行了修改,把标准中特殊值NaN更改为无穷大或无穷小(和符号位相关)。
2.3 参考模型的编写
参考模型用于完成和DUT 相同的功能,其输出用于与DUT 的输出相比较。根据脉动阵列内部体系结构以及定制化的浮点数算术运算规则,设计并完成验证平台中的参考模型。基于脉动阵列运算要求,需要实现乘法和加法的模型建设。
乘法模型使两个16位半精度浮点数相乘能够得到一个32位的单精度浮点数;加法模型是为了实现32位单精度浮点数相加的功能。在模型搭建之前就需要引入利用C 语言写好的乘加运算模型,把它们当作函数来使用。
对于在参考模型中所使用的乘法和加法函数而言,在函数形式上这两个函数后面都有3个参数,第一个参数表示结果输出,第二和第三个参数都表示输入。因为乘法器实现的是两个半精度浮点数乘法运算,因此两个输入都是16bit,其输出结果就变成了32bit的单精度浮点数。加法器的两个输入是乘法器的输出,即都是32bit。在对加法树进行建模时需要用到加法器。
由于在设计并考虑到对脉动阵列进行建模时整个代码页太多,我们在编写参考模型时,使用了extern virtual task关键字。其中的extern是为了控制class的长度,如果在class中想使用一些函数或者任务,用这个关键字就可以另起一页代码去编写代码行较长的函数或者任务,这样就可以避免一页代码行过多;virtual就是简单的虚函数功能;task是简单的任务关键字。这样只需要在新的代码页中编写有关脉动阵列的模型代码即可。
参考模型的编写思路如下:
首先是实现一个DOT 中的乘法运算,并把运算结果寄存到一个数组中,这种数组需要声明32个,数组的位宽为32bit。完成一个DOT 中的乘法运算后,便是开始建立加法树模型,从而得出最终结果。经过上文的介绍后,我们可以得知,加法树的底部是由32个乘法运算结果而组成的,而这些结果已经存入了所声明的数组中。从数组中取出这32个乘法运算结果并作为加法器的输入,按照两两结合的方式进行相加,其过程如1.3小节中所描述的一致,此时所需要的加法器数量为16个。经过相加后便可以得出16个数据,这16个数据会存入到新声明的数组中去,然后从新声明的数组中取出数据,继续两两相加,这时候会比上次减少8个加法器,以此类推,最终会得到一个输入结果,即一个DOT 的输出,最终使用了32 个乘法器,31 个加法器。
其次,由于脉动阵列中划分了32个DOT,因此只需要在上述步骤情况下,利用一个for循环即可实现整个脉动阵列的运算过程。经过运算后,32个DOT 会产生32个运算结果,这些运算结果也会根据DOT 的排列顺序而进行排序,从而组成一个向量。例如,处于脉动阵列中最左边的DOT,那么它产生的结果就会在结果向量的第一个位置,同理,其它DOT 产生的结果就会在结果向量中相对应的位置,这一功能只需要利用移位便可以实现。具体的实现过程是,每得到一个32bit的数据时,都把它排在向量的最左端,然后把它和向量的高992 位进行组合,利用System-Verilog中的{},以此往复32次。
上述的步骤就可以实现脉动阵列的模型建立,高效且简洁明了,对于其他人而言也方便理解。如果存在相似结构的脉动阵列,此模型也可以直接进行移植使用,达到复用的效果。
3 UVM 验证结构
使用DPI可以很方便地连接C 代码,这些C 代码可以读取激励、包含一个参考模型或仅仅扩展SystemVerilog的功能。此外,验证平台还使用到了UVM,它是由Cadence、Mentor和Synopsys联合推出的新一代验证方法学。
3.1 关于UVM
UVM 主要是一个以SystemVerilog语言为基础的一个库。因为UVM 具有层次化的结构、可随机化的激励、可高度复用的验证平台等优点广泛应用于数字集成电路(IC,integrated circuit)的验证过程之中[14-15]。验证平台因为使用了SystemVerilog这一面向对象语言来构建,所以UVM也继承这一特点。在UVM 中,是通过树形结构来管理各个类,各个类是派生于uvm _object或者uvm _component[16],而UVM 中常用类的继承关系如图5所示。这些通用验证部件不仅具有可配置性、封装性、可重用等优点而且还具有phase自动执行特性。Phase是将component分割成几个不同的执行阶段并且按照一定的先后顺序来执行。Phase的引入,在很大程度上避免了由代码书写不规范而引发的问题。Phase中最常用的由build_phase、connect_phase、run_phase等。在3.2和3.3小节中,详细讲述了本实验的验证平台结构。
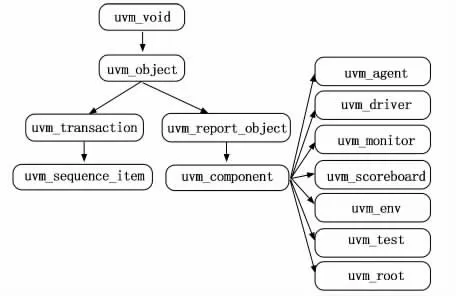
图5 UVM 中常用类的继承关系
3.2 UVM 验证平台组件
UVM 中各个组件有着不同的功能,包括产生激励、发送激励、采集信号、模拟待验模块以及输出接口数据对比等。基于本文脉动阵列的结构,其验证平台采用UVM 组件进行设计,具体各个组件的名称及其功能见表1。这些组件的继承关系会在1.3小节中进行描述。
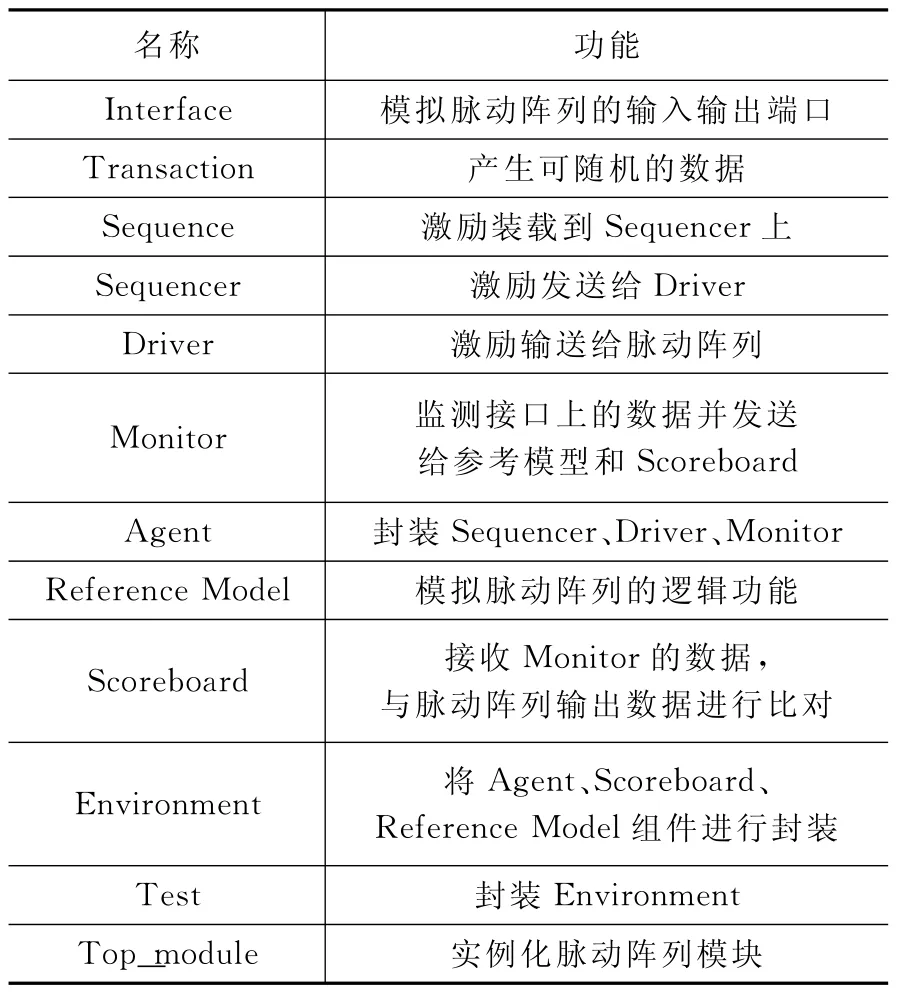
表1 验证平台组件及其功能
3.3 验证平台内部通信
当设计一个基于UVM 的验证平台时,需要完成各个组件的代码编写,其次把编写好的各个组件进行实例化并利用事务级建模(TLM,transaction level modeling)[17-18]方法进行组件之间的通信。其组件之间具体的通信以及验证平台部分功能实现过程:
1)首先是输入阶段,在Transaction中声明受约束的激励,激励通过Sequence发送给Driver,之后再由Driver发送给接口,此时Monitor对输入接口进行监测,并把监测结果传送给Reference Model,这一步便完成了验证平台的输入数据包发送过程以及脉动阵列的激励产生。
2)输入阶段完成后,脉动阵列和Reference Model便会产生各自的输出。脉动阵列的输出结果也是由Monitor进行监测脉动阵列输出接口上的数据得到的。Reference Model的输出结果和脉动阵列的输出结果会各自写入预置好的FIFO(先入先出,first input first output)中,在Scoreboard会把两个FIFO 中的数据进行读取并进行对比,这一阶段便完成了输出阶段。
3)由于一些信号在时序上需要满足特定的情况,采用在Interface 中添加断言的方式去保证信号时序符合要求[19-20]。
根据3.1小节图5中UVM 类的继承关系、3.2小节表1中的验证平台组件以及上述的内部通信过程,本文设计的验证平台框架如图6所示。每个组件名字下面括号内的标签就是其父类,例如Driver继承于uvm_driver,Reference mode继承与uvm_component,其他组件同理。
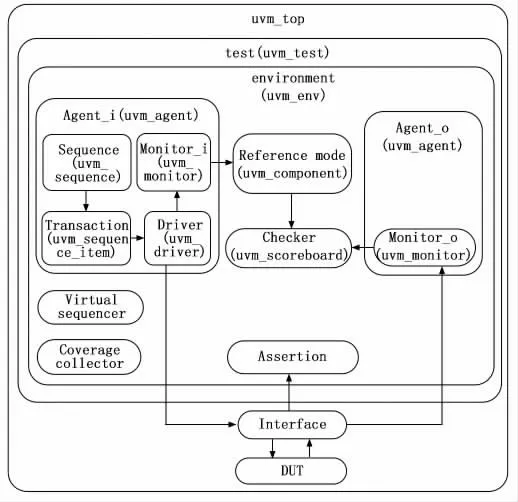
图6 基于UVM 的验证框架
4 实验结果与分析
本节介绍在完成脉动阵列的验证平台搭建后,DUT 和参考模型的输出结果在Scoreboard中进行对比的过程,并对比对结果进行分析。
4.1 结果对比过程
激励经过输入给脉动阵列和参考模型后,脉动阵列以及参考模型会把各自的输出结果送进预先定义好且不同的FIFO 中。把脉动阵列的输出结果定义为actual放进一个FIFO 中,参考模型的输出结果定义为expect放进一个FIFO 中,之后分别从两个FIFO 中取数据来进行比对。
在出现错误的时候,先记录下actual与expect,定位所发送出现对比错误的数据并记录下来。找到目标数据后,根据设定的浮点数算术运算标准进行人工计算,把人工计算结果分别与脉动阵列和参考模型输出的结果进行对比,然后以此来分析错误原因并修正错误。修正错误后,把记录下的数据以定向激励的形式再一次发送给验证平台,若此时输出为正确结果,则继续进行验证,否则重复上述工作。
4.2 验证结果分析
在本次测试用例中,给出一个随机种子,其中有1 000个受约束的随机数据。在所给的随机数据中包括vain(A矩阵)、vbin(B矩阵)、ainvld(A矩阵有效信号)、binvld(B矩阵有效信号)。vain、vbin接口在测试的时候分为符号位、指数位、尾数位。把这三部分进行随机约束遍历,进行这一操作是为了实验后阶段能够收取较好的覆盖率。随机约束遍历情况如表2所示。
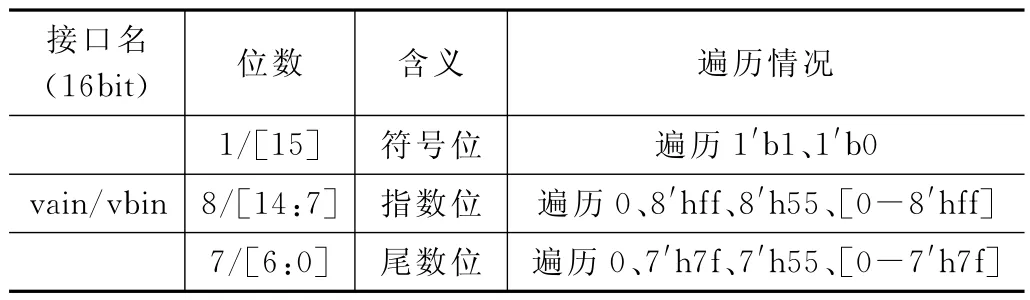
表2 不同接口数据遍历情况
在实验测试用例里的随机数据包全部使用完之后,需要查看FIFO 中是否还有残留的未发送的随机数据包。在实验中,经过多次随机种子后,其FIFO 中的残余数据结果如表3。
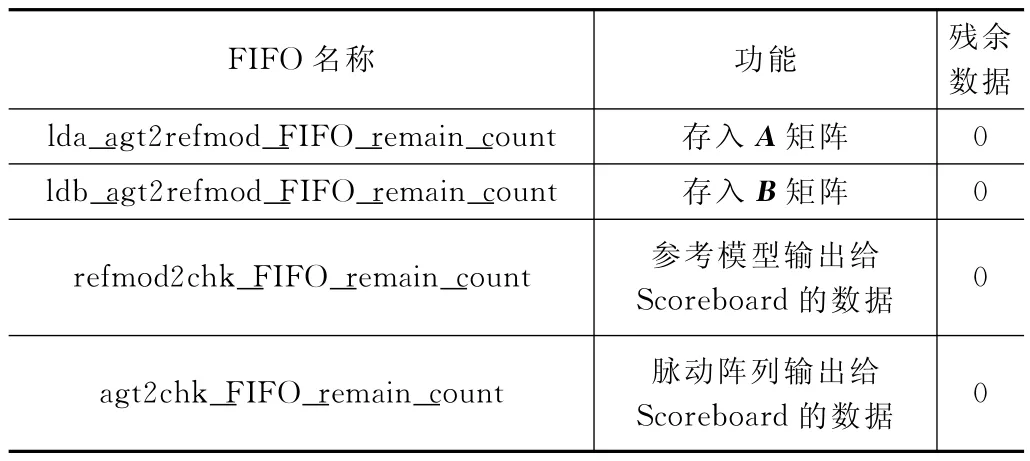
表3 各个FIFO 内数据情况
运行不同的测试用例的仿真或者不同的种子都会生成专属的覆盖率数据。经多次仿真且覆盖率经过合并后,根据覆盖率情况证明达到了验收要求。表4所展示的是最终的总的覆盖率结果,每个覆盖组代表着脉动阵列中的一个功能点。
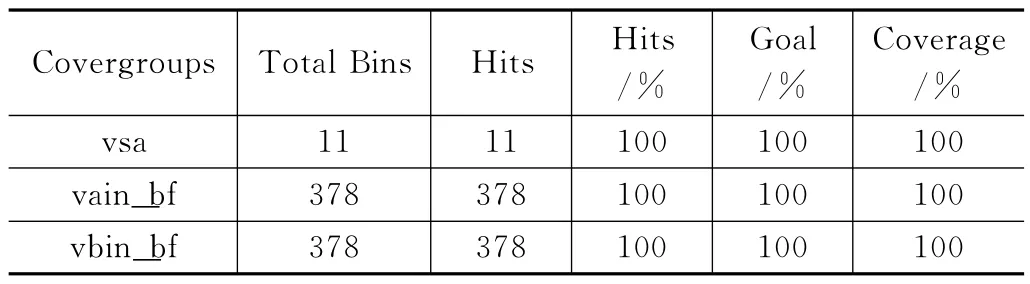
表4 功能覆盖率结果
5 结束语
本文利用DPI-C 技术与UVM 相结合的方法搭建一个脉动阵列的验证环境。该验证环境利用了SystemVerilog事务处理能力强大的优点以及C 实现模型成熟、稳定、重用性高的优点,相对于传统的验证方法,平台结构较为简单,可以快速搭建参考模型。本文实验通过运用覆盖率驱动策略,将验证进度进行量化,最终达到功能覆盖率100%的验证目标,提高了验证的完备性和准确性。另外,本文的验证方案不仅能够实现验证环境的复用,而且测试用例也能实现更高验证层次的复用,可以大幅缩短片上系统芯片的开发周期。
