基于节点优化的改进全局路径规划A*算法
2023-07-06董凯锋宋俊磊莫文琴惠亚娟
卫 彦,晋 芳,董凯锋,宋俊磊,莫文琴,惠亚娟
(1.中国地质大学(武汉)自动化学院,武汉 430074;2.复杂系统先进控制与智能自动化湖北省重点实验室,武汉 430074;3.地球探测智能化技术教育部工程研究中心,武汉 430074)
0 引言
随着机器人技术的发展,机器人的功能从最开始的只能在固定位置做重复循环工作发展到如今可以根据指令在室内室外进行移动作业,并且能够解决突发问题,移动机器人的能够实现的功能越来越丰富,移动机器人应用的领域越来越多,在很多行业已经使用移动机器人来代替人工作业。除了简单的搬运、运输工作,移动机器人还可以代替人类去做一些危险的工作,例如高空作业、危险探测、野外勘探等。随着新冠疫情的爆发,人们再一次认识了移动机器人的重要性。疫情期间的很多物资运输采用移动机器人就可以减少感染风险。
比起以前单纯靠人力和物力进行的工作,移动机器人的工作效率和工作准确率都更高,因此在在全球的经济贸易交流越来越频繁的时代,很多传统的依靠人工的方法逐渐被淘汰,掌握机器人的核心技术就相当于抓住了经济的命脉。室内移动机器人是我们在生活中能够经常接触到的移动机器人。目前一些超市、餐厅已经大规模投入使用移动机器人完成送餐工作;扫地机器人也是目前很多人会购买的家用室内机器人。在2022北京冬奥会期间,投入使用了很多室内移动机器人。例如食堂采用了送餐机器人给运动员和工作人员们送餐;提供给媒体居住的酒店里应用了室内移动机器人消毒技术;各大场馆还有防疫用的巡控移动机器人。
室内移动机器人要完成任务,要解决的重要问题之一就是怎么去目标地点,也就是路径规划问题。路径规划是移动机器人工作的重要保障之一,是移动机器人完成导航和其他任务的前提[4]。路径规划是指按照一定的标准,根据起点和终点规划出一条规避障碍物的路径。路径规划的主要内容为:预设地图环境模型,输入起点坐标和终点坐标,路径规划的输出则是基于已设定的地图模型得到的连接起点坐标和终点坐标,并且不与地图模型中的障碍物产生碰撞的最优有效的序列点,最终把序列点连接将变成机器人在实际环境中的运动轨迹。路径规划算法分为全局路径规划算法和局部路径规划算法,常用的全局路径规划算法有A*算法、蚁群算法、遗传算法和粒子群算法,常用的局部路径规划算法有人工势场法、速度障碍法和动态窗口算法等[1]。
在路径规划算法中,A*算法作为一种启发式算法,有着广泛的应用领域[3]。但是A*算法存在着路径不平滑、拐点多、路径非优等问题[2]。针对这些不足,学者们研究出了很多改进型A*算法:文献[3]通过改进评价函数的计算方式和权重比例,减少生成路径中的拐点,使生成的路径更平滑。文献[4]在改进启发函数的基础上对生成的路径做五次多项式平滑处理,减少了A*算法的搜索时间,缩短了路径长度。文献[5]通过将3×3的搜索邻域扩展成7×7,减小了路径转折角度。文献[6]在障碍物膨胀处理的基础上使用射线法简化冗余点,减少了50%以上的路径转折点。文献[7]和文献[1]通过对A*算法生成的路径进行节点优化,除去冗余点,缩短了路径长度。上述方法都减少了A*算法生成路径的转折点,减短了路径长度,但是上述文献中去除冗余点的方法在某些情况例如贴近障碍物的路径比较多的情况下的路径优化效果不够明显。对此,本文在扩大搜索邻域基础上引入一种随机数去除冗余点的方法,使得路径长度更短,访问的节点个数更少,运行时长更短,从而使得在贴近障碍物的路径比较多的情况下的路径优化效果更好。
1 A*算法原理
A*算法是启发式算法中常用的一种算法,通常在栅格地图中进行路径规划,对于当前节点周围的点使用评价函数对其进行评估,选择评价函数最小的点作为扩展节点,搜索到终点就停止搜索,最后将所有选择的点在栅格地图上连接起来,从而得到一条规避障碍物的完整路径。A*算法路径规划可以分为以下两个部分进行:环境建模和路径规划。
1.1 环境建模
A*算法在路径规划前需要做环境建模,既生成有障碍物信息的栅格地图,如图1所示,白色区域为可通行区域,黑色区域为障碍物区域。栅格地图通常以矩阵或者图片的方式保存。对于图片格式的栅格地图,通常读取图片的像素获得一个像素值矩阵即可使用。

图1 栅格地图
完成环境建模后,需定义算法在该栅格地图中的搜索方式。常用A*算法中,移动机器人通常在栅格地图上采用3×3邻域搜索,有8个运动方向,即东、南、西、北、东南、东北、西南、西北,如图2所示。将以当前节点为中心的3×3邻域中的节点作为备选节点,经过比较后选择扩展的节点。因此在这种3×3邻域搜索中,路径是由很多段长度为1或者1.4个单位长度的路径组成的。
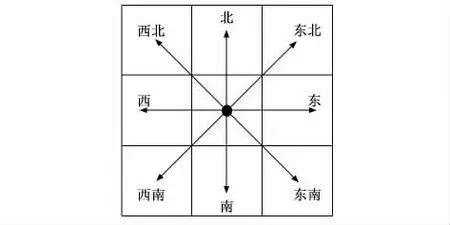
图2 移动机器人的8个运动方向
1.2 A*算法路径规划
接着在建立好的栅格地图上实现路径规划。A*算法路径规划有两个列表,OPEN 列表和CLOSE 列表。A*算法路径规划的基本思想是,从起点开始,将周围3×3邻域中的八个扩展点加入到OPEN 列表,选择OPEN 列表中评价函数最小的点作为下一个节点,并将选择的节点记录到CLOSE 列表,直到搜索到终点为止。A*算法的评价函数为:
其中:f(n)是当前点的评价函数,g(n)是起点到当前点的实际代价即实际路径长度,h(n)是当前点到终点的最小估计代价,通常采用当前点和终点的欧氏距离表示,即:
其中:(x_n,y_n)是当前节点的坐标,(x_t,y_t)是终点的坐标。
A*算法的路径规划实现流程如图3 所示,具体步骤如下:
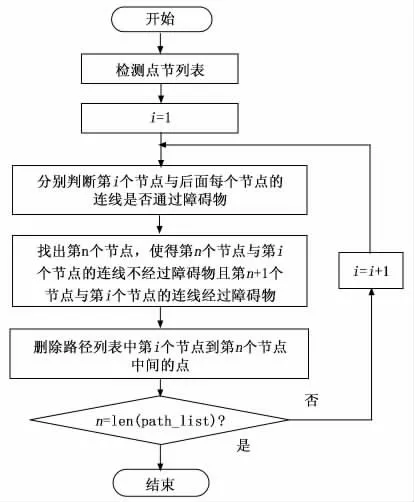
图3 A*算法路径规划实现流程
1)创建一个OPEN 列表和一个CLOSE 列表,将起点加入到OPEN 列表。
2)将除了CLOSE 列表中的节点和障碍物以外当前节点的3×3搜索邻域中的节点加入到OPEN 列表。
3)对OPEN 列表中的节点进行评估,选出评估函数值f最小的节点n作为扩展节点。
4)将已访问的节点n放入CLOSE 列表,并判定n是否是终点,如果n不是终点,就回到第二步,如果n是终点,就结束此次路径规划。
2 改进A*算法
A*算法路径列表中存在冗余点,生成的路径不是最优路径,且转折点较多,转折角度较大,路径不够平滑,这些问题会导致A*算法在应用在移动机器人运动控制时,存在多余拐弯,加大控制难度的问题。为了优化此问题,本文提出一种在搜索邻域扩大到5×5的基础上随机数选择节点去除冗余点的改进A*算法。
2.1 冗余点去除方法
目前常用的去除冗余点方法有两种:方法A 和方法B。方法A[15]就是先遍历一遍路径列表,找到其中的拐点,将起点、拐点和终点放在一个列表中,从起点开始,依次连接起点和各个拐点,若第n个拐点与起点的连线不经过障碍物且第n+1个拐点与起点的连线经过障碍物,去除列表中起点与第n个拐点之间的拐点。再依次验证列表中其他拐点之间的连线,最后提取剩余拐点,按照顺序连接,生成路径。如图5 所示,针对[S,1,2,3,4,5,6,T]的路径列表,生成一个只包含起点、拐点和终点的列表[S,1,2,3,5,T],以起点为例,依次连接起点S和点3、点5、终点T,起点和点3的连线不经过障碍物且起点S和点5的连线经过障碍物,去除掉点1、点2。在去除全部冗余点之后,列表为[S,3,5,T],最后按顺序依次连接列表中拐点,生成如图蓝色路径,路径长度为7.16个单位长度。
方法B[4]与方法A 的原理类似。在路径列表中从起点开始,依次连接起点和列表中的节点,若第n个节点与起点的连线不经过障碍物且第n+1个节点与起点的连线经过障碍物,去除列表中起点与第n个节点之间的节点。再依次验证列表中其他节点之间的连线,最后提取剩余节点,按照顺序连接,生成路径。如图5所示,针对[S,1,2,3,4,5,6,T]的路径列表。在去除全部冗余点之后,列表为[S,3,5,T],最后按照顺序依次连接列表中拐点,生成如图红色路径。
方法A、B 去除冗余点的原理如图4 所示。图中len(path_list)代表节点列表的长度。两种方法判定冗余点的方法是一样的,只不过方法A 在去除冗余点之前,多了一步寻找拐点的操作,接着在拐点列表中去除冗余点。
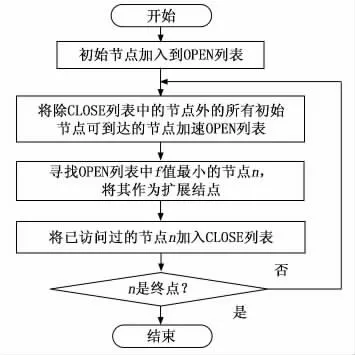
图4 方法A 和B的工作原理流程图
方法A、B在某一段路径上的优化结果如图5所示。图中由于非拐点的节点较少,方法A 和方法B优化出来的路径是一样的。在稍复杂一些的环境中,方法A 在路径长度的优化效果上会比方法B 的差,但是方法B 的运算次数会比方法A 多。

图5 A*算法和方法A、B去除冗余点效果对比
以上两种去除冗余点的方式都有一定的局限性。方法A 会忽略掉非拐点,非拐点之间的连线也有不穿越过障碍物的可能。忽略掉非拐点会导致去除掉冗余点之后还是存在着路径非最优解的问题。而方法B运算的次数太多,图6中的路径列使用方法A 只用运算7次,而方法B 需要运算13次,程序运行时间更长。因此需要对去除冗余点的方法进行优化,找到一种结合两者优点的节点优化的方法。

图6 5×5搜索邻域
2.2 扩大搜索邻域
A*算法采用3×3邻域扩展节点的方法,一共有8个扩展方向,转折的角度不够灵活,产生一些无效的转弯路径,导致生成的路径并且不是最优路径。
针对这个问题,本文将3×3的邻域扩展成5×5的邻域,即16个扩展方向,如图6所示。
以图7的5×5地图为例,图中黑色圆点为当前节点,红色节点为目标点。在使用3×3邻域搜索时,由于搜索方向过于局限,导致从当前节点到目标点的路径为向东北一个单元格再向北一个单元格,如图中黑色实线所示,有一次转折,在转折处需要转北偏东45°才能到达目标点,路径长度为2.4个单位长度。但是在使用5×5邻域搜索时,只需要朝着北偏东26.57°运动2.2个单位长度就可以直接到达目标点,如图中虚线所示,有效减少了转折次数,转折角度相比于3×3邻域搜索也有所减小,更便于移动机器人运动。

图7 5×5搜索邻域优化效果
但是扩大搜索邻域并不能完全解决A*算法路径列表中有冗余点的问题,如图8所示,5×5邻域搜索出来的路径需要先朝正北运动1个单位长度,再朝北偏东26.57°运动2.2个单位长度到达目标点,而7×7邻域搜索出来的路径只需要朝北偏东18.44°运动3.16个单位长度就能到达目标点。5×5邻域搜索出来的路径会比7×7邻域搜索出来的路径长,且多一个转折点。但是一味地扩大搜索邻域,并不适用于所有地图,而且优化效果有限,可以看到搜索邻域越大,与原先生成的路径组成的三角形的顶角越大,这样优化的路径是比原先的路径短不了太多。一味地扩大搜索邻域还可能会加大程序的计算量,使程序运行时间变长。因此需要在适度扩大搜索邻域的基础上去除冗余点。

图8 7×7搜索邻域优化效果
2.3 冗余点去除方法改进
目前广泛使用去除冗余点的方法A、B有一个共同的缺点:过早地去除掉某些点会导致优化效果不好。如图9所示,图9中路径长度为6.06个单位长度,比图5中的三条路径都要短。但是在方法A 中,点2在起点和点3的连线不经过障碍物的情况下被删除,而点4和点6则早早地因为不是拐点被删除掉了;在方法B 中点2在起点和点3的连线不经过障碍物的情况下被删除,点4和点6分别是因为点3和点5、点5和终点T 的连线不经过障碍物被删除。图5中的路径适合每两个节点之间进行连线验证,这样确实可以得出图9中的路径,但是局限性太大,并不是所有路径都适合两个两个地验证,因为在复杂一些的环境中,A*算法规划出来的路径和其最优解对比,最优解在某一小段上的路径的节点优化的数字并不是固定的,在第一段中连接了第i个节点和第i+a个节点,去除了这两个点中间的节点;在第二段中连接了第n个节点和第n+b个节点,去除了这两个点中间的节点。因此,固定每几个点之间连线验证,是有非常大的局限性的。
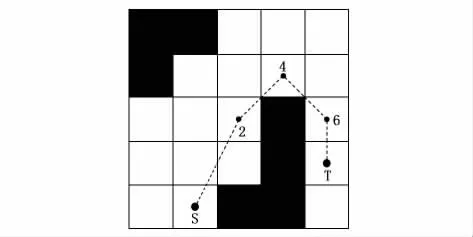
图9 优于方法A 和方法B处理结果的路径
为了解决这个问题,本文在将搜索邻域扩大至5×5的基础上提出一种引入随机数的去除节点列表冗余点方法。将搜索邻域扩大至5×5之后,有效减少了路径列表中的节点,在5×5邻域搜索出来的路径列表中做节点优化会减少很多运算次数,有效优化程序运行时间。该方法的流程如图10所示。具体步骤如下:
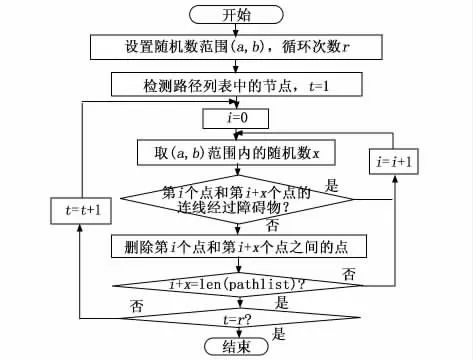
图10 本文优化算法去除路径列表冗余点流程图
1)依据地图的大小,设定一个随机数的取值范围(a,b),设置一个循环次数r。
2)针对路径列表,随机取(a,b)范围内的数字c,验证和的连线是否经过障碍物,若不经过障碍物,则删除列表中和之间的点。
3)按照顺序依次检测列表中的点,重复2),直到检测到,整理剩下的点,依次连接列表中的点,生成路径,计算路径长度。
4)循环步骤2)和步骤3)r次,最后选择路径长度最短的一条路径输出。
在面对转折点较多的路径时,本文的算法中随机数这一步可以保留方法A、B中被提前删除掉的点,找出更优的路径。
3 仿真验证
为了验证本文改进A*算法的有效性和优化效果,本文在不同环境建模的栅格地图上进行了仿真实验,仿真软件平台为Python3.9,硬件平台为Intel(R)Core(TM)i5-9500CPU@3.00GHz,RAM 16GB。
首先,创建一个30×30的栅格地图,障碍物占该地图的30.6%,其中每个栅格代表一个单位(1m)。设置待规划路径起点坐标为(5,17),终点坐标为(27,2)。使用3×3搜索邻域A*算法在此地图上进行路径规划,得到的路径如图11所示。可以看出A*算法拐点较多,有8个拐点,存在明显的冗余点。

图11 A*算法运算结果
其次,使用常用的去除冗余点的方法A 和方法B 去除冗余点,结果如图12(a)、(b)所示。方法A 生成的路径拐点数减少到5个,方法B生成的路径拐点数减少到4个。可以看出使用两种方法后,路径拐点较常用方法减少、长度有所缩短,但是仍然有优化的空间,比较数据结果见表1。
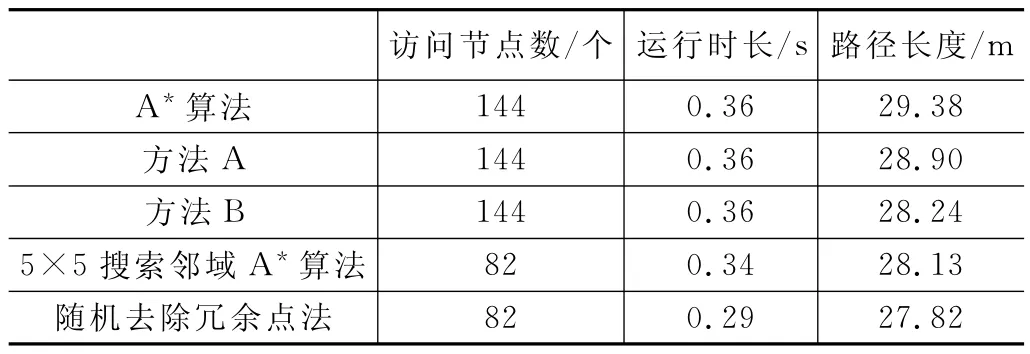
表1 30×30地图中算法运行结果对比
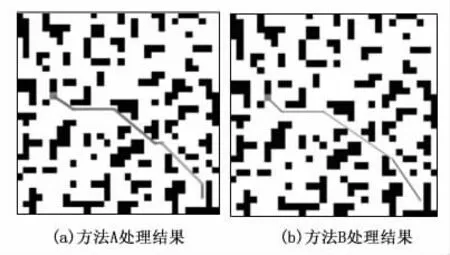
图12 方法A 和方法B处理后的路径
然后在此地图上使用将搜索邻域扩大至5×5的A*算法进行路径规划,结果如图13(a)所示。路径长度比A*算法生成的路径长度短,但转折点比方法A 和B 生成的路径多。接着使用本文提出的随机去除冗余点法对图13(a)所示路径进行优化,在随机数取值范围为(2,8)、循环次数为10的情况下,运行结果如图13(b)所示。
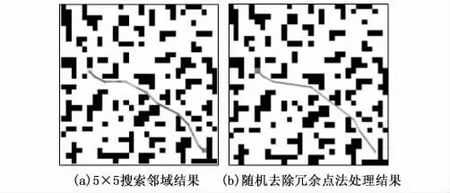
图13 5×5搜索邻域A*算法与随机去除冗余点法处理后的路径
整理上述A*算法、方法A、方法B、5×5 搜索邻域A*算法与随机去除冗余点运行结果,对比如表1所示。表1中运行时间、运行长度均为运行了10次的平均数。可以看到本文提出的随机去除冗余点法运算出的访问节点个数、运行时长和路径长度均优于另外3种算法,证明随机去除冗余点法在减少了A*算法生成的路径节点数和长度,减短了运行时长。
为了验证本文算法在不同方向路径上的优化效果,接着在此地图中,选择不同方向的几组起点和终点进行验证,结果如表2、表3和表4所示。
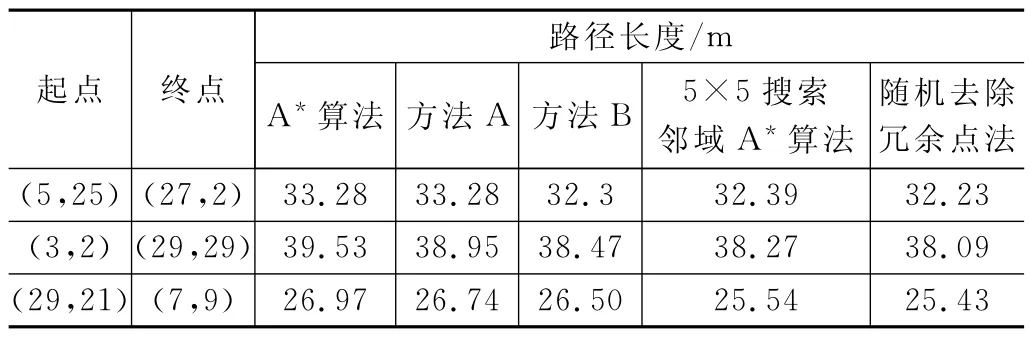
表2 多组起点终点的路径长度对比
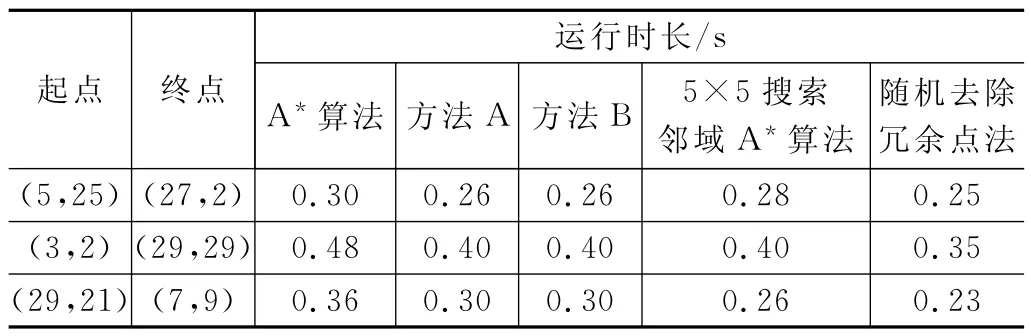
表3 多组起点终点的运行时长对比

表4 多组起点终点的访问节点个数对比
可以看出,在此30×30栅格地图中,面对不同方向的路径,本文的算法在路径长度、运行时长和访问节点个数上均优于其他算法。结合上述4个表的数据,本文算法运行结果对比A*算法,路径长度平均减少了4.46%,运行时长平均减短了24.83%,访问节点数平均减少了39.93%。
4 结束语
针对A*算法拐点和冗余点较多的问题,本文在搜索邻域扩大至5×5的基础上提出了一种引入随机数去除节点列表冗余点的改进A*算法。通过仿真验证并与其他算法对比,证明了本文算法有效改进了A*算法拐点和冗余点较多的问题,缩短了路径长度、减少了访问节点的个数并有效减少了运行时间。但是该方法还存在一定的不足,如运行的结果与随机数取值范围、循环次数有很大的关联,不同的地图适合的随机数取值范围和循环次数不同等。随后将进一步研究影响最优随机数取值范围和循环次数的因素,找到适用于所有地图的随机数取值范围和循环次数推导公式,使得该方法适用于更多地图。
