基于磁致伸缩的电磁超声钢板机械性能检测方法

韩 飞，赵新航，陈锴迪，高 飞，王逸凡，徐 昕

（上海航天电子技术研究所，上海 201109）

0 引言

钢板机械性能的测量是航天工业和科学研究的基础，同时屈服强度、抗拉强度、和延伸率也是被最广泛研究的。即使成分相同的钢板，也可能由于不同的生产工艺，其强度也会不同。破坏性测试方法是昂贵的［1-2］，且仅限于抽样测试，这些缺陷刺激了无损检测（NDT）方法的出现。由于钢板的磁特性，如磁导率、矫顽力等等与其机械性能的变化有关，因此国内外提出了几种电磁无损检测方法，包括巴克豪森噪声法、涡流法、增量磁导率法等［3-5］。

邱等人提出了一种基于脉冲涡流的多特征融合方法来检测钢板的屈服强度，该方法最大相对误差为7.39%［6］。李等人采用增量磁导率来检测钢板的屈服强度，最大相对误差为8.14%［7］。受趋肤效应的影响，这两种方法更适用于较薄的钢板。文献［8 -9］则利用巴克豪森噪声来测量钢板的力学性能，但巴克豪森噪声信号易受到高频噪声的干扰，因此该方法只能使用在低频状态下。由于电磁超声具有可以激发多种波形，且可以工作在更高宽的频率范围等优点，这些激发了基于电磁超声的机械性能检测研究。

针对于上述原因，本文提出了基于磁致伸缩的电磁超声检测方法。通过控制电磁超声系统发射端和接收端电流的变化，分别得到基于磁致伸缩效应的电磁超声曲线和基于逆磁致伸缩效应的电磁超声曲线。分别从两条曲线上提取出特征参数，并验证了特征参数用于检测的可行性和实验的可重复性。分别采用了基于逐步回归的预测方法和基于RBF的预测方法，且这两种方法对于机械性能的检测具有较高的准确率，从而表明了本文所提出的检测方法的有效性。

1 原理

1.1 微观结构与机械性能

钢板是由无数形状不同的小晶体构成的多晶体，这些小晶体称之为晶粒。大量研究表明，晶体的位错和滑移运动与晶粒的大小影响着钢板的机械性能［10］。所谓晶粒的位错，其实是微观层面上的一种缺陷，造成该缺陷的原因是材料内部某些原子的无序排列。滑移则是通过位错的移动来实现的，滑移的结果是微观上众多的原子逐渐从一个稳态到达另一个稳态，在宏观上表现为塑性形变。产生滑移所需要的临界摩擦力为上文提到的屈服强度。当屈服阶段完成之后，晶体的位错和滑移运动也会随之增加，使得钢板的塑性变形更加困难，这也是影响抗拉强度的原因之一。

晶粒大小，即平均晶粒尺寸，也影响着钢板的机械性能。通常来说，平均晶粒尺寸越小越均匀，钢板的机械性能就越好。20世纪中期，学者Hall提出如下公式来表征晶粒与滑动带的关系，即：

式中，K为常数，d为晶粒的尺寸，但当时并未给出x的大小。之后英国利兹大学的Petch 在此基础之上，提出了Hall-Petch公式［11］：

式中，σs为材料的屈服强度，σ0为单位位错产生的晶格摩擦力。该公式明确指出晶粒的尺寸越小，屈服强度就越高。

抗拉强度与晶粒尺寸的关系与屈服强度类似。Stroh公式描述的是断裂强度与晶粒尺寸的关系［12］，表达为：

式中，σc为断裂强度，kc为Petch斜率，γ为有效表面能，G为切变模量，ν为泊松比。当材料为脆性金属材料时，断裂强度即为抗拉强度；而材料为塑性金属材料时，抗拉强度与断裂强度间也具有经验关系，即：

式中，σb为抗拉强度，φ为常数。由公式（3）～（5）可以看出随着晶粒尺寸的减小，抗拉强度也会越高。

1.2 微观结构与磁致伸缩正、逆效应

磁致伸缩分为磁致伸缩正效应和磁致伸缩逆效应。磁致伸缩正效应是指当钢板处于磁场中时，其形状和尺寸会轻微伸长或缩短，用磁致伸缩系数λ表征。磁致伸缩正效应从微观层面来说，究其原因是：磁畴和磁畴壁的运动（原子轨道磁矩和自旋磁矩的交换、耦合作用等导致原子间的距离发生变化），从而带来磁弹性能的变化［13］。上述微观层面的变化对λ100和λ111方向的磁致伸缩系数有明显影响（立方单晶体沿着［100］轴磁化的磁致伸缩系数为λ100，沿着［111］轴磁化的磁化系数为λ111），具体函数关系［14］如下：

Ca、Cb为材料的弹性刚度常数，b1、b2为磁弹性能的耦合系数。因此可以建立磁致伸缩正效应与材料微观结构的关系。

对于磁致伸缩逆效应来说，同样发生在钢板磁化状态下，其本质是磁导率的变化。图1展现了钢板的磁化曲线与其磁导率曲线的关系，即磁化曲线某点的斜率为该磁场状态下的钢板磁导率。

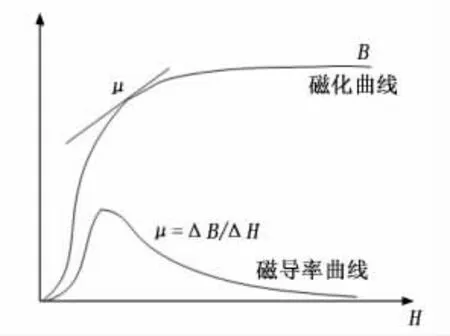
图1 钢板的磁化曲线与磁导率曲线

从微观角度来说，也是由于外磁场的作用，使得钢板内原子轨道磁矩和自旋磁矩发生交换、耦合作用，而导致原子间的距离发生变化［15］。除此之外，不同的钢板由于微观结构的不同，使得磁化曲线和磁导率曲线不同，即晶粒大小也影响着磁致伸缩逆效应。通常情况下，晶粒越粗大、晶界间越平滑，则晶界处的摩擦力越小，那么磁畴壁就越容易运动，磁致伸缩逆效应就越容易发生。同时，晶粒的取向也很重要，平行于易磁化轴的晶向越多，则磁致伸缩逆越容易发生。

1.3 机械性能与磁致伸缩正、逆效应关系建立

由于机械性能与磁致伸缩正效应、磁致伸缩逆效应都受晶粒、磁弹性能等微观参数影响，因此可以将这些微观参数用Pi表示，同时将表征磁致伸缩正效应的特征参数用Bm表示，表征磁致伸缩逆效应的特征参数用Cn表示，那么Bm和Cn可以［16］被表示为：

同理，屈服强度Rp，抗拉强度Rn和延伸率A可以表示为：

联立式（8）～（12），将微观参数消除，可以得到机械性能与磁致伸缩正效应、磁致伸缩逆效应的关系：

由于磁致伸缩正效应、磁致伸缩逆效应的本质是磁致伸缩系数和磁导率的变化，且这些变化不易直接测得，但根据它们的变化可以得到相应的EMAT 信号。图2就表明了磁致伸缩系数与EMAT 信号之间的关系［17］。

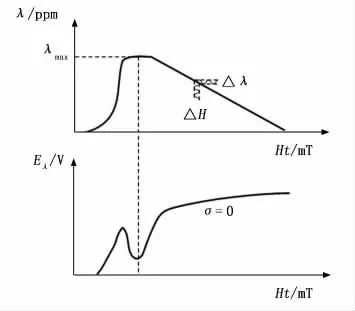
图2 磁致伸缩系数曲线与EMAT 信号的关系

当EMAT 线圈探头内通入交变脉冲电流时会产生小的交变磁场，该交变磁场叠加到静态偏置磁场中，钢板会产生交变的磁致伸缩应变。即磁致伸缩系数曲线中某点的斜率越大，那么该点所对应的EMAT 信号幅值越大。由图2可知，当磁致伸缩应变达到最大时，该磁场下对应的EMAT 信号幅值最小。通过以上分析，基于磁致伸缩正效应的电磁超声检测系统对钢板检测时，通过观察EMAT 信号幅值随外加偏置磁场的变化关系，可以反映钢板的正效应特性。

对于逆效应来说，磁导率和EMAT 信号之间的关系［18］可由公式（16）体现：

式中，dm为压磁系数，μ0为真空磁导率。由公式（16）可知，磁铁作用于钢板时，其磁导率会发生变化，该变化导致了EMAT 检测系统接收端的磁通量的变化，从而导致了检测系统接收端的线圈产生的感应电压的变化。通过以上分析，基于磁致伸缩逆效应的电磁超声检测系统对钢板检测时，通过观察EMAT 信号幅值随外加偏置磁场的变化关系，可以反映钢板的逆效应特性。因此，可以将反映正、逆效应的参数Bm和Cn替换成从EMAT 信号上提取的相关特征。

总之，钢板的微观结构将机械性能与磁致伸缩正、逆效应特性联系在一起。通过测量并分析基于上述效应的EMAT 信号这一建模思路，可以用来实现对钢板机械性能的预测，检测原理如图3所示。

图3 基于磁致伸缩-逆磁致伸缩的EMAT 系统检测原理

2 系统硬件设计

由电磁超声发射电路、电磁超声换能器和电磁超声接收电路组成的检测系统如图4所示。以单片机为核心的发射电路发射一个200kHz的脉冲串。该脉冲串经过功率放大电路和阻抗匹配网络后，传输到发射线圈。在直流电磁铁的作用下，发射线圈能在被测试样表面激发出一系列频率相同的振动信号，即超声波。当超声波被传送到接收线圈时，线圈会产生一个幅值很小的感应电压。经过滤波和放大电路，电信号可由数据采集卡采集。

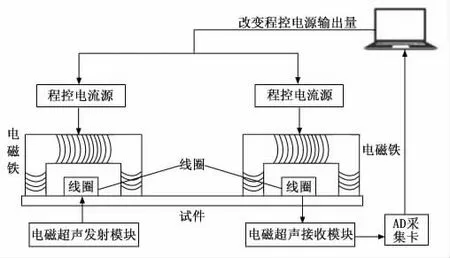
图4 基于磁致伸缩-逆磁致伸缩的电磁超声检测系统

3 系统软件设计

3.1 逐步回归

特征参数的数量影响着机械性能预测的准确率，因此会从原始信号中提取相当多的特征参数，这些特征参数可以最大限度的反映原始信号的全部信息，如在上一小节中一共提取了十个特征。但这种大规模提取特征参数的方式不但会提高回归模型的复杂程度，还会带来多重共线性问题造成过拟合。因此提出使用逐步回归的方法来避免特征过多而带来的不利影响。

在构建拟合模型的途中，先要对所有特征参数进行评估，不同的特征参数对机械性能的贡献度不同，所以需要对特征参数进行合理的挑选，来决定最终的拟合模型中包含的特征参数。通常，特征参数的引入和剔除主要分为单方向法以及逐步回归法，其中单方向法包括前向法和后向法两种［19］。

前向法的特点是把特征参数一个一个引入模型。具体过程是：先把对机械性能有最大贡献度的特征参数选入模型中，然后，在未被引入的特征参数中，将与机械性能有最大关联的特征参数引入模型并进行F检验，循环往复，直至满足停止准则。后向法是另一种拟合模型的特征参数选择方法，但过程与上文提到的前向相反：第一步将所有特征参数都选入模型，然后对每个特征参数进行F检验，若不通过检验，就剔除该特征参数，使用剩下的特征参数重新拟合一个函数模型，之后再次进行上述过程，直到模型中所有特征参数都能够通过检验。

逐步回归法则是将前向和后向两种方法相结合，即将特征参数逐个选入到回归模型中，且每次只选入一个对机械性能贡献最强的特征参数，每完成一次前向的过程，就进入后向的过程，即对当前模型中存在的全部特征参数进行F检验，把对机械性能贡献不强的特征参数剔除出模型，并开始下一步前向过程，直到剩下的特征参数不满足条件为止。最终得到的模型既不会丢失对机械性能贡献强的特征参数，也不会引入对机械性能贡献不强的特征参数。总的来说，逐步法可以归纳成如下3个步骤，如图5所示。

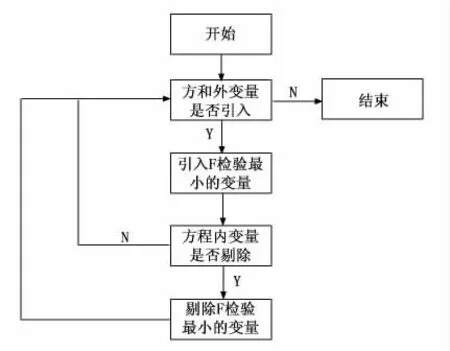
图5 逐步回归流程图

1）对有限个特征参数，分别同机械性能y建立函数模型，即：

式中，a0为常数项，ai为特征参数的回归系数。根据回归方程，逐个计算特征参数xi的检验统计量F值，记为F1，F2，…，Fn。取其中最大值，若该值大于F分布临界值表中对应的数值，那么就将该特征参数xi引入。

2）对模型外的特征参数依次做F检验，来检验其对机械性能的贡献能力，如果有许多个特征参数通过了F检验，我们选择其中F值最大的一个特征参数引入模型。若无特征参数通过检验，则终止引入过程。

3）将原先模型中存在的特征参数和步骤2中选择出的一个新特征参数相结合，建立新的模型，对该模型中每一个特征参数做F检验，假设有许多特征参数未能通过F检验，选择其中F值最小的，并将其剔除。重复整个过程，直到模型中所有特征参数都可以通过检验。之后，再次回到第二步，开始新的挑选特征参数过程。

为了衡量逐步回归的建模效果，本文选用均方根误差、最大相对误差、预测合格率和平均绝对误差作为评估指标。

1）最大相对误差：最大相对误差（MRE，maximum relative error）指的是预测结果和真实值之间的最大绝对误差，定义为：

2）均方根误差：均方根误差（RMSE，root mean square error）用来表征样本的离散性，一定程度上可以反映预测的准确率。表达式为：

式中，N为样本总数。

3）预测合格率：预测合格率代表最大相对误差小于某一设定值的样本通过率。根据合作厂家要求，设定预测合格率Q10，即最大相对误差小于10%的样本通过率，表达式为：

式中，N10代表最大相对误差小于10%的钢板数量。

4）平均绝对误差：平均绝对误差（MAPE，mean absolute percentage error）是将所有预测样本的绝对误差求和再平均，可用下式表示：

3.2 RBF神经网络

在最近的几年间，关于机器学习的技术快速发展，越来越多的人将该技术应用到电磁无损检测中，即应用神经网络构建特征与机械性能之间的映射关系，但使用的神经网络多为BP。BP存在逼近能力差、速度慢等缺点，且在样本量较小时，容易造成过拟合问题。由于本文所使用的样本总量为50，属于小样本范围，因此并不适用于BP。鉴于这一问题，本节将利用适用于小样本的神经网络来构建预测模型。

20世纪末，美国学者提出径向基函数（RBF，radical basis function），按照其观点，RBF进行样本训练的本质就是寻找一个多维曲面，该曲面可以拟合任意训练中的样本，而网络预测的过程则是在该曲面中寻找一个最适合的点，且可适用于样本量较少的情况［20］。

RBF神经网络的神经元模型如图6所示，其节点激活函数采用径向基函数，通常定义为空间任一点到某一中心之间的欧氏距离的单调函数。

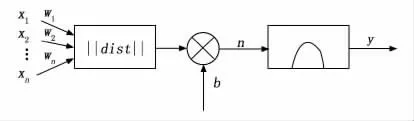
图6 径向基神经元模型

该神经网络激活函数的一般表达式为：

RBF的网络结构一般由三个作用完全不同的层构成。输入层由许多感知单位构成，它们将网络与外界因素联系起来并线性传递到第二层；第二层网络是隐含层，其目的是将输入数据通过对称的非线性函数进行转换，该层采用的神经元局部响应函数多为高斯函数；输出层的作用仅仅是将隐含层处理后的数据进行线性优化。基于以上所述的网络结构，RBF与BP相比，前者有着较快的学习速度和较强的数据拟合能力，因此作用于样本数较小，样本分布较紊乱的情况也有不错的预测性能。

本文创建了具有三层结构的RBF作为钢板机械性能估算模型，该模型包括输入层、隐含层和输出层，如图7所示。

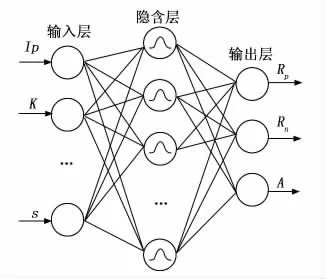
图7 RBF神经网络预测模型

每层的神经元个数和相关参数受到如下的条件约束：

1）被测试件的机械性能为不同的三项，因此RBF的输出层神经元个数为3。

2）输入层的神经元个数与特征参数的数量有关，即节点数等于特征数。

3）隐含层的神经元个数在很大程度上影响着模型的估算精度。根据这一情况，在建立隐含层的过程加入了循环的算法，即在网络训练中，每增加一个神经元，就计算当前的机械性能预测误差。如果误差不满足于期望目标，那么隐含层就不断的加入神经元，直到预测误差降低到期望目标以下，或者神经元的个数达到设定阈值；不然，就停止循环，该流程如图8所示。

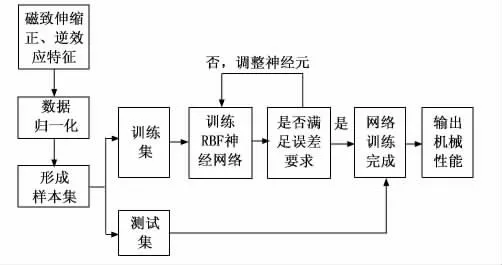
图8 机械性能预测流程图

4 实验结果与分析

4.1 实验步骤和方法

第三节简单介绍了用于检测钢板机械性能的系统，为了获得基于磁致伸缩正效应和磁致伸缩逆效应的EMAT 信号，EMAT 检测系统发射端和接收端的电磁铁、曲折型线圈及钢板的相对位置如图9所示。当发射端通以变化的直流电，且接收端通以恒定的直流电时，此时获得基于正效应的EMAT 信号。相反，则是获得基于逆效应的EMAT信号。

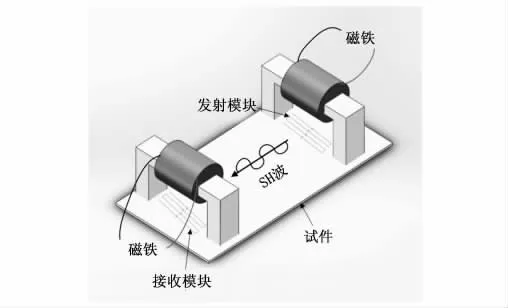
图9 基于磁致伸缩正、逆效应的EMAT 检测系统

超声波在运动到接收端的过程当中，其能量不是一成不变的，而是与位移有关，即EMAT 信号的强度与发射、接收端之间的距离相关，并且随着位移量的增加，EMAT信号强度呈递减趋势，可用式（23）描述：

式中，As为信号强度，As为发射、接收端之间的距离。图10为不同距离时的超声波信号，符合式（23）的规律。但两者之间的距离过小会造成包络的重叠，影响直达波峰峰值的提取，从而影响预测精度。为了保证实验是可重复的，应该严格控制该变量，考虑到被测试件的尺寸，在此实验中规定为200mm。

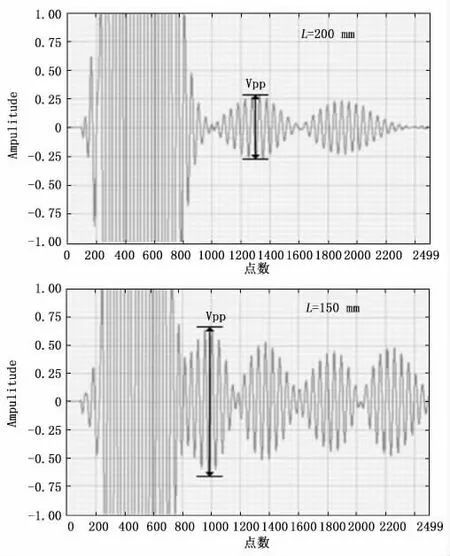
图10 不同距离超声波信号对比

4.2 实验结果

实验钢板是某合作钢厂以冷轧方式生产的同一批但不同钢种的低碳薄板，且这些薄板内部没有应力。这些钢种多为常见的类型，普遍使用在各种领域。具体的相关参数见表1，这批薄板的尺寸为300mm＊200mm。

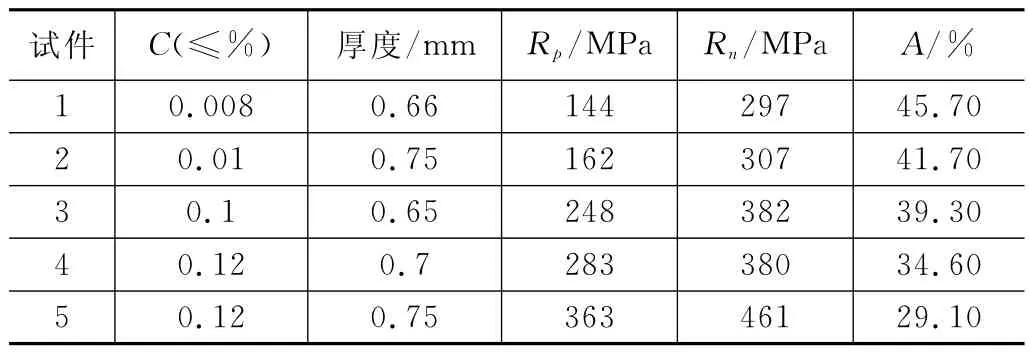
表1 被测试件的基本性能参数

由于本文研究的是基于正效应和逆效应的钢板机械性能检测方法，因此需要分别实验，从而获得基于上述两种效应的EMAT 曲线。之后将分别从正效应曲线和逆效应曲线上提取特征，因此特征分为正效应特征和逆效应特征。

首先，将接收端的电磁铁通以恒定电流，使接收端外部磁场不变。接着将变化速率为0.02A／s的电流通向发射端，此时会获得基于正效应的EMAT 曲线，且每块试件重复测量10次。以试件1为例，EMAT 曲线如图11所示。

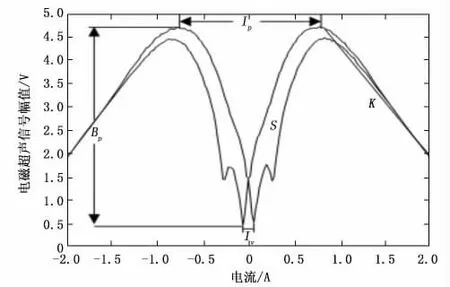
图11 基于磁致伸缩正效应的EMAT 曲线

由于每块试件基于磁致伸缩正效应的曲线的变化趋势都大致相同，但它们的峰峰值Ep，两峰值电流差Ip，两谷值差Iv，面积S和斜率K有明显区别，因此初步选取这五个特征为正效应特征。

Person公式用来计算不同变量之间的相似度，其绝对值越高，代表两者之间越相关，因此可以用来判断特征选取是否合理。表2则反映了正效应特征与机械性能之间的Person相关系数。

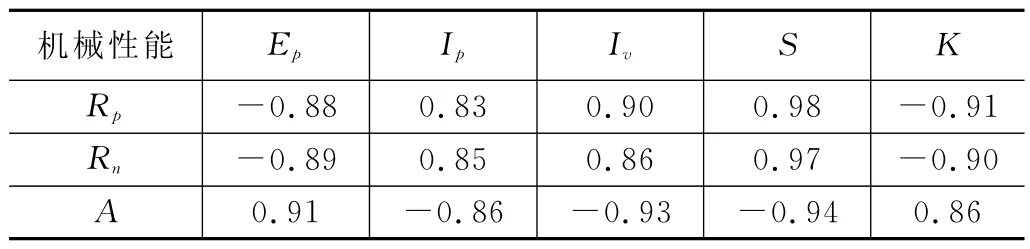
表2 正效应特征与机械性能的相关系数

从表2中可以得知，五个特征分别与三项机械性能指标呈很高的相关性，即Ip、Iv、S与屈服强度和抗拉强度之间的相关系数均大于0.83，呈正相关，而Ep、K与屈服强度和抗拉强度的相关系数均小于-0.88，呈逆相关；Ip、Iv、S与延伸率间的相关系数均小于-0.86，呈逆相关，而Ep、K与延伸率间的相关系数均大于0.86，呈正相关。

在实验的可重复性方面，则用相对标准偏差（RSD，relative standard deviation）来验证。这五个特征的相对偏差见表3。由表3 可知，所有正效应特征的RSD 均小于10%，因此可以代表实验具有较好的重复性。

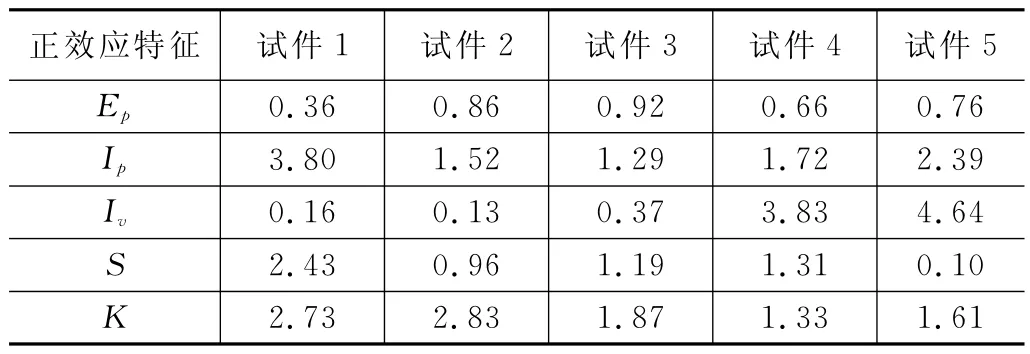
表3 正效应特征的相对标准偏差表 %

对于逆效应特征的提取，则与上文中正效应特征类似。首先，将发射端通以恒定电流保持发射端的外部磁场不变，将变化速率为0.02A／s的电流通向接收端，此时会获得基于逆效应的EMAT 曲线，且每块试件重复测量10次。以试件1为例，曲线如图12所示。由于每块试件的逆效应曲线的变化趋势都大致相同，但它们的峰峰值ep，两峰值电流差ip，两谷值差iv，面积s和斜率k有明显区别，因此初步选取这五个特征为逆效应特征，且这些特征已在图12 中标出。

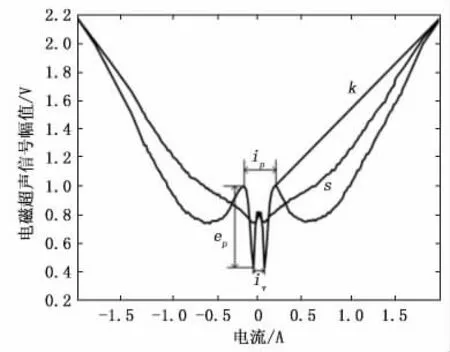
图12 基于磁致伸缩逆效应的EMAT 曲线

表4则反映了逆效应特征与机械性能之间的Person相关系数。从表中可以得知，五个特征同样与三项机械性能指标保持很高的相关性，即ip、iv、ep与屈服强度和抗拉强度间的相关系数均大于0.80，呈正相关，而s、k与屈服强度和抗拉强度间的相关系数均小于-0.83，呈逆相关；ip、iv、ep与延伸率间的相关系数均小于-0.83，呈逆相关，而s、k与延伸率间的相关系数均大于0.85，呈正相关。

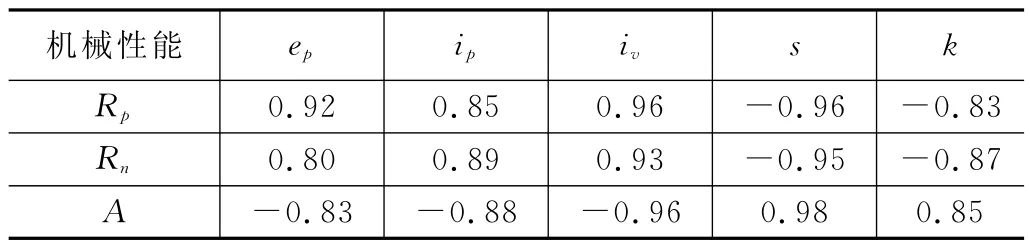
表4 逆效应特征与机械性能的相关系数

逆效应特征的RSD 见表5。由表5可知，所有逆效应特征的RSD均小于10%，因此可以代表逆效应实验数据具有良好的重复性。

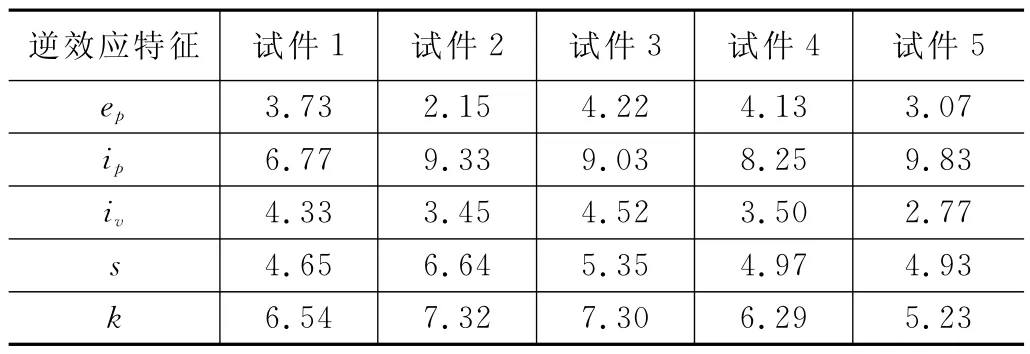
表5 逆效应特征的相对标准偏差表 %

4.3 实验分析

将表1提到的五块试件在同一条件下分别测量十次，共计50个样本。选取其中四块试件（试件1、2、3、5）的40个样本用来建模，剩下（试件4）的10个样本用于预测。建立的关于屈服强度Rp、抗拉强度Rn和延伸率A的逐步回归方程如下：

上述三个回归模型的R2分别为0.96、0.95、0.90。由公式（24）～（26）可知，正效应特征中的面积S、峰峰值Ep、斜率K和逆效应特征中的谷间距iv对屈服强度Rp最为敏感；正效应特征中的面积S和谷间距Iv对抗拉强度最为敏感；逆效应特征中的面积s、峰间距ip和斜率k对延伸率最为敏感。将余下的样本输入到上述三个逐步回归模型中，4个评估指标结果如表6所示。

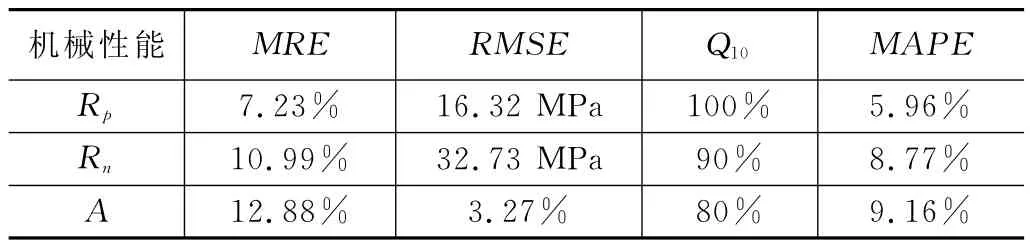
表6 试件4预测结果表

由表中结果可见，在磁致伸缩正、逆效应曲线上提取特征值点，训练逐步回归模型，构建正、逆效应特征值与屈服强度、抗拉强度和延伸率的映射关系，可以实现对铁磁性材料机械性能的预测。屈服强度和抗拉强度估计合格率Q10均大于90%，延伸率的估计合格率Q10大于80%。除此之外，屈服强度、抗拉强度和延伸率的平均绝对误差均小于10%。

对于RBF模型，这里仍取钢板1、2、3和5用于训练，试件4用于测试，使用该模型对机械性能的预测结果如表7所示。

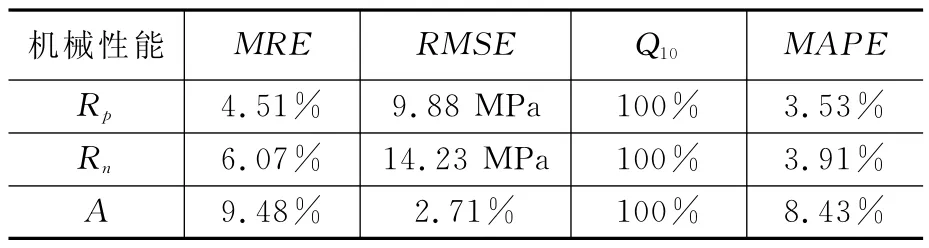
表7 RBF神经网络预测结果

与上文所使用的逐步回归方法相比，机械性能预测结果得到改善。屈服强度、抗拉强度和延伸率的RMSE均大幅减小。对于抗拉强度来说，预测合格率Q10提高了10%；对于延伸率，预测合格率Q10提高了20%。此外，相对平均误差也有所减小。结果证明，基于RBF的预测模型具有局部逼近能力强和非线性处理能力强的特点，可以用于样本量较少的预测场合。

5 结束语

本文设计了基于磁致伸缩正效应和磁致伸缩逆效应的机械性能检测方法。首先以微观结构为桥梁，分析了EMAT 信号与机械性能之间的关系。在实验验证部分，分别从正效应曲线和逆效应曲线上各提取了五个特征，并对特征进行了有效性分析，即相关系数绝对值均达到0.8以上，同时也进行了实验可重复性分析，即实验数据的相对标准偏差均小于10%。

在建立特征参数与机械性能之间映射关系的过程中，首先使用了逐步回归的方法，目的是解决特征参数过多而导致维度灾和多重共线性的问题，经过实验验证，该方法可以保留影响最显著的特征参数且具有较高的预测精度。在机器学习方面，针对于小样本情况，提出使用RBF 神经网络。经过实验验证，该预测模型与逐步回归模型一样，预测精度良好。总之，上述两种建模方法都说明了基于磁致伸缩正、逆效应的EMAT 检测方法用于预测机械性能的有效性。