新型粉罐车流化床气室和气道结构参数研究与结构优化
2023-07-05曾亿山
许 伟, 曾亿山, 燕 浩
(合肥工业大学 机械工程学院,安徽 合肥 230009)
0 引 言
粉罐车用流化床是一种广泛应用于工业粉料运输行业的能够使粉料流态化的封闭装置。所谓粉料流态化就是压缩气体透过流化床,使流化床上的粉料相互分离而悬浮于空气中,使粉料具有一般流体的特性,以便于运输,减少浪费和环境污染。当前的粉罐车采用布袋结构,使得粉料流化效果不理想,流化死区面积大,粉料剩余率较高等问题都制约着粉罐车的发展。
关于流化床的基础理论各国学者已展开诸多研究[1-3],发现流化床流化面的流体速度是影响流化床流化性能和粉料流化质量的关键因素,同时也影响着粉料卸载的工作效率和粉料残余率[4]。流化床的几何结构是影响气体分布均匀的关键因素,若流化床面积较大,而床层较薄,则流化床层易出现沟流等非正常流化状态;若流化床面积较小,床层较厚,则易出现气泡和节涌等非正常流化状态;若物料直径差异较大,则易出现分层等非正常流化状态[5-6]。因此,为了提高流化床粉料卸载效率和减小粉料残余率,有必要加深对粉料运输领域流化床内流体速度分布均匀性的研究。
目前常用的优化方法包括田口算法、正交算法等[7-8]。文献[9]将改进的粒子群优化算法和有限元分析的田口算法用于优化安装有涡旋压缩机的六相铜转子感应电动机,以实现最小的制造成本和起动电流、最大的效率和功率因数;文献[10]通过田口算法和多元回归优化一种空气分配器通道的结构参数,得到了结构参数的最佳方案及其预测阻力系数;文献[11]使用标准时间分数扩散方程分析气体在多孔介质中的扩散浓度分布,发现气体分子在多孔介质中传输的弛豫时间在10-8~10-6s的范围内;文献[12]将田口算法应用于垂直轴潮汐涡轮机的水动力特性优化中,优化后的垂直轴潮汐涡轮机的功率系数比基准设计提高了24%,流动分离大大减少。以上这些对田口算法的应用为本文分析流化床流体速度分布均匀性提供了理论基础。
计算机技术的发展推动了计算流体力学(computational fluid dynamics,CFD)在流体计算仿真领域的应用,大量的研究证明该方法能够准确预测流体流动特性[13]。文献[14]使用CFD开发了一个用于模拟通过各种几何形状管道结构中细颗粒的气动传输模型,验证了在水平和垂直气力输送中颗粒尺寸的分布完全不同;文献[15]用CFD方法,以氧化铝为输送材料,进行气力密相输送试验,由此分析了固体体积分数、气体/固体速度等重要参数在管道横截面上的变化;文献[16]在单温度多孔介质模型的基础上修正了双温度多孔介质模型,通过CFD模拟了固定床反应器多孔介质中气体的流动,模拟结果与实际数据吻合较好;文献[17]采用多孔介质和CFD-DEM2种方法模拟一种反应器中氦的热水力特性,结果表明2种方法模拟的传热特性大致相同。
关于流化床流动特性有诸多研究。然而,在粉料运输领域,提高流化床内气体分布均匀性方面的研究较少,尤其是流化床气室和气道结构对流体分布的影响。因此本文以粉罐车流化床为研究对象,基于田口算法分别设计了16种新型流化床气室和气道结构参数方案。通过信噪比及方差结果分析各结构参数对响应的影响,获得了各参数的贡献率及其最佳参数组合。相关研究成果可为粉罐车流化床结构设计提供参考。
1 粉罐车流化床工作原理
传统粉罐车用流化床采用布袋结构,如图1a所示,压缩气体直接进入均匀分布在罐体底部的布袋,布袋四周均是流化面,由于布袋所用布料的气阻相同,因此压缩气体使靠近气室部分的粉料先进入流化状态,布袋末端的粉料则难以流化,同时两侧布袋对其外侧粉料输送的气体分布不均匀,因此存在流化死区。

图1 粉罐车流化床结构模型
新设计的粉罐车用流化床在气室中间添加了一块隔板,电机驱动空压机产生的压缩气体经进气管道向罐体两头的气室输送,气室内的气体经过隔板的缓冲形成流速均匀的气体后,流过铺有透气布的新型气道区域形成细微、均匀的气流进入粉料层,使粉料流态化,如图1b所示。优化后的气道除透气布压紧位置存在死区外,总体部分死区面积明显减少,由传统粉罐车约11%死区降至约6%。
流化床上的气道均匀地分布在罐车气室的圆弧上。由于进气管道与气道方向相垂直,因此经空压机压缩后的高速气体进入气室扩散后流到气道入口处时,不同气道处的气体速度仍然存在一定的差异,进而影响粉料的整体流化效果。因此,本文将不同测量点气体的速度分布相对其平均速度的偏离程度称为气体的速度分布均匀性,该值越小,气体的速度分布相对其平均速度的偏离程度越低,速度均匀性越好,气道入口处和流化面的速度分布均匀性表达式分别为:
(1)
(2)

2 田口算法试验设计与数值模拟
2.1 田口算法的试验设计
田口算法是应用在试验设计和确定参数对系统效率的影响方面使用最为广泛的统计方法之一[18]。与传统的优化方法注重于提高系统的平均性能相比,田口算法更注重于通过对所有可能试验中的一部分典型试验进行计算,以获得更好的参数组合,从而深入了解控制因子的变化对系统效率的影响。
本文气室部分的结构影响气道入口处的速度分布,气道部分的结构影响着粉料流化面的速度分布,2个部分的结构都会影响流化床的流化效果,因此为了深入了解不同结构参数对系统响应的影响,分别对气室和气道部分的结构参数进行田口算法试验设计。该设计分为以下4个步骤[19-20]。
(1) 确定分析对象。本文需要通过数值分析研究以下2个目标对象:① 流化床气室和气道的结构参数对流化床内气体速度分布均匀性的影响;② 分析不同结构参数的贡献率,确定结构参数的最优组合。
(2) 确定响应特性。本文选取vu和vu′作为田口算法的响应,通过CFD数值模拟得出每个小气道入口处和流化面流体ui和ui′,由(1)式、(2)式计算得到各个方案的vu和vu′值。
(3) 确定因素及其水平。流入气道的气体是经过有分隔板的气室缓冲扩散后输入的,因此气道入口处气体的速度均匀性取决于气室的结构参考。气室部分选取V、K及δ作为影响流化床内气体速度分布均匀性的关键因素进行分析,如图2a所示。其中:V为流化床气室的整体容积大小;K为隔板右侧气室容量与左侧气室容量的比值;δ为隔板上端部的直线部分与气室上壁面的距离。气室结构参数及其不同水平值见表1所列。

表1 气室、气道结构参数及其水平值
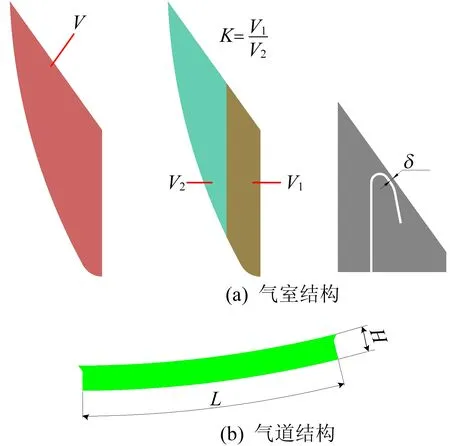
图2 气室和气道结构
流化床气道的结构参数是影响流化面气体速度分布均匀性的关键因素,为了分析流化床气道的几何参数对流化性能的影响,确定气道高度H和气道弧长L这2个关键的结构参数进行分析,如图2b所示。所选的因素及其具体的水平值见表1所列。
(4) 选择合适的正交阵列。对于气室选取的三因素四水平的试验方案,传统的试验方法需要进行64次试验才能全面地分析所有因素水平的影响,田口算法提供了一种基于正交阵列的试验方法,仅需16次试验即可均匀地考虑到每个因素的影响,有效地提高了试验效率。赋值后的三因素四水平正交阵列见表2所列。

表2 气室和气道结构参数正交试验方案
对于气道选取的两因素四水平的试验方案,同样采用上述田口算法提供的正交阵列。赋值后两因素四水平的正交阵列见表2所列。
2.2 数值模拟
2.2.1 计算区域及边界条件
为了分析流化床气室和气道的结构参数对气道入口处气体的速度分布均匀性和床层内部压缩气体流动特性的影响,对基于田口算法设计的16种气室和气道结构参数进行数值计算。单侧计算区域如图3所示。进口边界条件为2.34 m/s质量流进口,出口设为9 kPa静压出口。当能量残差小于10-6且其他变量的残差均小于10-3时,可以认为计算收敛,数值计算结果有效。

图3 单侧计算区域
为了使仿真结果更为准确,现将工程实际中覆盖在气道上层的透气布在仿真计算区域中设置为多孔介质层。仿真模拟时,多孔介质层可以在气道入口处提供一定的透气阻力,使得进入流化床气道的气体不会出现在气道入口处就通过设定的仿真出口全部流失,导致流化床中后半部气体速度衰减消失,使仿真结果更贴合实际情况,提高了仿真结果的真实性和准确性。
2.2.2 控制方程
粉罐车流化床优化设计为工程领域实际问题,RNGk-ε湍流模型是应用较为广泛且精度较高的解决工程实际问题的湍流模型。其控制方程[21]如下。
连续性方程为:
(3)
动量方程为:
(4)
湍流脉动动能方程为:
(5)
湍流耗散率方程为:
(6)
涡黏系数和生成项分别为:
μt=Cμρk2/ε,
Pk=μtU·(U+UT)-
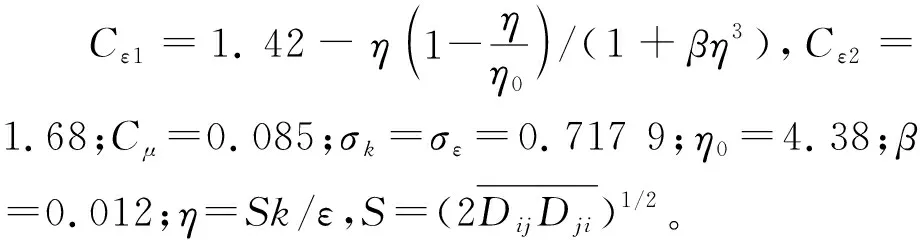
2.2.3 网格无关性验证
本文借助ICEM软件对计算区域进行网格划分,如图4所示,为了消除网格数量对计算结果的影响,以V为0.19 m3、K为0.5、δ为3 mm的气室和L为180 mm、H为17 mm的气道试验L1为例,进行网格无关性验证,其他试验方案采用相同的网格划分方法。

图4 计算区域网格图


表3 网格无关性验证
0.001 832、R2=5.596%,vu′下降了0.000 445、R2=4.897%;方案4与方案3相比,vu下降了0.00 367、R2=1.868%,vu′下降了0.000 185、R2=1.396%;方案5与方案4相比,vu仅下降了0.000 095、R2=0.134%,vu′仅下降了0.000 069、R2=0.249%。但由于网格数量较多,所需的计算时间大大增加。因此,综合考虑时间成本和计算精度,选用方案4的网格数量进行数值计算。
3 结果分析
采用上述数值模拟方法,得到流化床内部气体流动和速度分布情况,由(1)式、(2)式计算出各方案气道入口处和流化面流体的速度分布均匀性,见表4所列。

表4 速度分布均匀性
3.1 信噪比分析
在田口算法中,需要计算的损失函数被转换成信噪比函数,利用信噪比函数可以确定测量值或计算值与期望值之间的偏差[22]。信噪比指目标值与标准差的比值,是一个度量稳健性的参数,本文为了得到最佳的响应特性,即气道入口处和流化面处流体的速度分布均匀性最小,采用望小特性(small the better,STB)的方法评估,表达式为:

(7)
通过田口算法对由数值计算得到的响应结果进行分析,得到V、K、δ3个因素各个水平对气道入口处流体速度分布均匀性的信噪比响应,见表5所列,其中Δ1为每个因子的最大信噪比平均响应值与最小信噪比平均响应值之差。结果表明δ(Δ1=11.67、r=1)对信噪比的效应最大,K(Δ1=6.07、r=2)对信噪比的效应次之,V(Δ1=3.58、r=3)对信噪比的效应最小。

表5 信噪比响应
V、K、δ3个因素各水平的均值响应见表6所列,其中Δ2为每个因子的最大均值平均响应值与最小均值平均响应值之差。结果表明δ(Δ2=9.159×10-3、r=1)对均值的效应最大,K(Δ2=5.158×10-3、r=2)对均值的效应次之,V(Δ2=2.067×10-3、r=3)对均值的效应最小。通过对信噪比及均值响应的分析,在本文流化床气室的结构参数中,δ对流化床气道入口处流体速度分布均匀性vu的影响最大,其次是K,V的影响最小。

表6 均值响应
通过同样的方法得到H、L这2个因素各个水平的信噪比响应见表5所列,结果表明L(Δ1=6.41、r=1)对信噪比的效应较大,H(Δ1=1.68、r=2)对信噪比的效应较小。H、L这2个因素各水平的均值响应见表6所列,结果表明L(Δ2=1.754×10-3、r=1)对均值的效应较大,H(Δ2=0.504×10-3、r=2)对均值的效应较小。因此,在流化床气道的几何参数中,L对流化床流化面处流体速度分布均匀性vu′的影响较大,H对其影响较小。
3.2 主效应图分析和最优参数选择
流化床最优结构参数的选择是基于对均值和信噪比响应的分析结果。通过分析各个因素不同水平组合的数值模拟结果和信噪比结果,并以主效应图的形式来表示,得到各个参数对质量特性影响的变化趋势和最优水平的选择。
V、K、δ的均值和信噪比的主效应图如图5所示,H、L的均值和信噪比的主效应图如图6所示。本文采用STB方法评估信噪比,因此均值主效应图中的极小值点对应最佳条件,无论望大还是望小的质量响应都需要保持最大的信噪比,因此信噪比主效应图中的极大值点对应最佳条件,从而确定气室的最优结构参数组合为:V=0.15 m3、K=0.5、δ=3 mm,气道的最优结构参数组合为:L=180 mm、H=17 mm。

图5 V、K、δ的均值与信噪比主效应图图6 L、H的均值与信噪比主效应图
当控制因素对质量特性产生的影响不相同时,即存在主效应,曲线的斜率越大,其主效应就越明显。
比较图5、图6中各因素均值和信噪比的主效应图,发现气室部分的V、K、δ和气道部分的H、L都存在对各自结构影响流化效果的主效应。其中气室部分δ对应的曲线斜率最大,主效应最明显,K对应曲线的斜率次之,V对应曲线的斜率最小,主效应最小。气道部分L的主效应量值较大,对质量特性的影响较大,H的主效应量值较小,对质量特性的影响较小。因此,在设计生产粉罐车用流化床时,对气室部分应更重视δ和K这2个结构参数的选择,气道部分应更注重L的选择。
3.3 信噪比残差图分析
通过残差图可以确定数值模拟的结果是否正确。残差图由残差的正态概率图、与拟合值图、直方图和与顺序图组成,气室和气道信噪比的残差图如图7、图8所示。残差的正态概率图可以验证信噪比残差是否满足正态分布,残差的正态概率图中的信噪比数据点紧紧围绕在直线周围,因此满足正态分布。残差的拟合值图可以验证残差是否具有随机分布性,拟合值图中的点随机地分布在零值的两端,因此模型具有良好的随机分布性。残差的直方图可以看出基本满足正态分布,且没有远离整体的条形,因此不存在异常数据点。残差的与顺序图显示图中的残差围绕中心线随机分布,残差不显示某种趋势,因此残差具有良好的独立性。

图7 气室信噪比残差图

图8 气道信噪比残差图
3.4 多元线性回归分析
为了综合考虑多因素的耦合作用对流化床进口处速度分布均匀性的影响,采用多元线性回归方法来拟合结构参数与速度均匀性的关联式,预测的关联式如下:
vu=-0.002 01-0.020 3V+
0.003 28K+0.015 64δ
(8)
vu′=-0.004 82+0.000 028L+
0.000 081H
(9)
从(8)式、(9)式中参数的系数可以看出,vu与K、δ成正相关,与V成负相关,vu′随着L和H的减小而减小。因此,为了得到较小的速度分布均匀性,气室部分应选择较小的K和δ,较大的V,气道部分应选择较小的L和H,这与上述田口算法的分析结果一致。
比较数值模拟得到的速度分布均匀性与预测关联式计算得到的速度分布均匀性,得到预测关联式的关联度如图9所示。

图9 线性拟合图
由图9分析得到,vu关联式计算的结果与数值模拟的结果最大误差不超过16.85%,vu′最大误差不超过18.39%。因此多因素耦合作用下流化床流体速度分布均匀性的预测关联式误差较小,具有较高的相关性。
3.5 速度分析
通过对数值模拟结果和田口算法信噪比结果进行分析,可知L1为理论上流化效果最好的试验方案;L13的流化效果最差。将L1、L6、L13数值模拟结果导出,得到气道内气体速度衰减曲线和速度场如图10所示。
观察各方案靠近零点位置的速度曲线和速度场可以看出,L1各气道入口处气体速度波动相对较小,L13波动相对较大。因此,L1的气道入口处气体速度分布均匀性较小,L13较大。
同时,进入气道内的气体首先在气道入口处进行一次速度衰减,然后沿Z轴方向气体速度进行均匀稳定的衰减。L1流化床内的气体在气道入口处损失较小,大部分气体沿着气道向后半部流动,速度衰减幅度较低的气体在气道中后半部对粉料进行流化,提高了流化床整体的流化效果。与田口算法得到的优化结果一致。
3.6 试验验证
对上述田口算法优化结果进行试验验证。将粉罐车流化床模型等比例缩小后进行实际粉料卸载试验,模型如图11a所示。试验过程如下:① 在试验开始前,将卸料阀关紧,将粉料厚度均均地铺在透气布上;② 通过空压机向试验模型两端的气室内压缩空气,压缩后的气体经过气室流向气道,使堆积在透气布上的粉料在压缩气体的作用下开始流化,当罐体内压强达到一定压强时,缓慢打开卸料阀,流化的粉料随着气体一起流向卸料口;③ 选择流化床透气布上粉料剩余量来比较各方案的流化效果。
L1和L13的试验结果如图11b、图11c所示。由图11b、图11c可知,L1透气布上粉料剩余量比L13明显减少,表明L1流化床的整体流化效果较好,这与田口算法结果一致。
4 结 论
本文以粉罐车用流化床为研究对象,基于田口算法分别对流化床气室和气道的结构参数设计了16种流化床结构,并建立了不同因素水平的正交试验。借助CFD进行了数值模拟,并将得到的速度分布均匀性作为响应,通过田口算法和多元回归方法对速度分布均匀性响应进行分析,得到如下结论:
(1) 信噪比结果表明气室部分3个结构参数中δ(Δ1=11.67、r=1)对信噪比的效应最大,K(Δ1=6.07、r=2)对信噪比的效应次之,V(Δ1=3.58、r=3)对信噪比的效应最小。气道部分的2个结构参数中L(Δ1=6.41、r=1)对信噪比的效应较大,H(Δ1=1.68、r=2)对信噪比的效应较小。各结构参数对速度分布均匀性的影响与其对信噪比的效应一致。
(2) 主效应图结果表明,气室部分隔板间隙δ的主效应最明显,分隔比K的主效应次之,气室容量V的主效应最小,气道部分气道弧长L的主效应量值较大,对质量特性的影响较大,气道高度H的主效应量值较小,对质量特性的影响较小。因此,气室部分的最优参数组合为V=0.15 m3、K=0.5、δ=3 mm,气道部分的最优参数组合为L=180 mm、H=17 mm。
(3) 多元线性回归结果表明,vu与K、δ成正相关,与V成负相关,vu′随着L和H的减小而减小。拟合图显示回归关联式计算的结果与数值模拟的结果存在误差,但误差较小,因此多因素耦合作用下流化床流体速度分布均匀性预测关联式的误差较小,具有较高的相关性。
