改进LSTM神经网络在极短期波浪时序预报中的应用
2023-07-05尚凡成李传庆朱仁传
尚凡成, 李传庆,2, 詹 可, 朱仁传
(1.上海交通大学 海洋工程国家重点实验室; 船舶海洋与建筑工程学院,上海 200240;2.上海船舶运输科学研究所 航运技术与安全国家重点实验室,上海 200135)
在实际海洋环境中,船海工程结构物由于受到海洋风、浪、流等环境因素的作用,会不断产生六自由度摇荡运动,而剧烈的摇荡运动对船舶海上作业产生一系列有害影响,包括对工作效率、安全性和船体结构、各种装备的影响等[1].如能在舰载机起飞和水下潜水器回收等船海结构物作业场景中提前预知船舶运动,给操作员提供辅助信息可以降低事故发生概率,提高作业能力和安全性.极短期预报利用船舶当前或过去的运动状态和某些己知的外部条件,使用某种方法来预测未来一段时间内船舶运动状态[2],以此为船舶海上航行以及海上任务作业提供控制输入和辅助决策信息,进而提高船舶在恶劣海况下的海上作业能力.
极短期预报具有实时性、不确定性的特点,通常基于波浪或者船舶运动历史的时历数据,使用时间序列分析方法对未来一段时期的波高或船舶运动姿态进行预报.20世纪80年代左右,经典的自回归模型等时间序列建模方法开始被广泛用于波浪和船舶运动运动预报[3],这些传统时序分析计算量比较小,但主要针对线性系统,对非线性较强的系统预报结果不佳,具有很大局限性.
随着人工智能技术的发展,神经网络、支持向量机等机器学习方法日趋成熟,因其可以任意精度逼近任意的非线性函数,拟合能力较强,所以逐渐受到研究者的关注.目前在时序分析中应用较为广泛的是循环神经网络(RNN)及其一系列变体,特别是长短期记忆(LSTM)神经网络,通过引入门控单元实现了长期记忆能力[4],预报效果较好.2016年Duan等[5]将经验模态分解技术与支持向量机回归结合对显著波高进行了预测研究.2017年Li等[6]使用具有外部输入的非线性自回归(NARX)神经网络对船舶运动进行了单步与多步时序预测.2019年刘煜城[2]、2020年张彪等[7]使用RNN对船舶运动姿态进行了预报研究.但上述研究大多仍局限在原有理论框架,往往使用单一神经网络模型,并且没有充分利用诸如频谱特征等已知信息,因此预报精度受限.而随着神经网络理论的发展,开始出现第三代人工智能概念[8],注重知识、数据、算法、算力的融合,强调先验知识与基本物理定律的重要性.
神经网络是一种通用的问题处理框架,其在各个细分领域上取得较好效果离不开与该领域专家知识的融合.另外神经网络是一个典型的“黑箱模型”,通过融合专业知识有助于进一步加深对神经网络底层原理的认识,同时有助于提高网络泛化性.随机海浪仍符合一定的统计规律,特定海区的随机波浪往往具有稳定的频谱特性.在波浪和船舶运动姿态预测中,频谱特性可以发挥更为重要的作用,值得探索时频域结合的极短期预报模型.本文受生成式对抗思想的启发,提出一种改进的LSTM神经网络架构,借助生成式对抗神经网络强大的数据增强能力,将波浪的频谱特性反馈至LSTM神经网络,通过融合频域领域先验知识,增强了神经网络对频谱特性的捕捉能力,成功实现了时域、频域信息耦合预报.同时该改进也可视为在原有LSTM模型的损失函数中加入正则化项,可有效防止神经网络训练中过拟合,提高模型泛化性.另外对频域信息的学习也便于去除神经网络由于偶然误差或其他原因产生的高频噪声分量,保证了神经网络输出的预报准确性.实验表明,该模型在波浪极短期时序预报上优于传统预报方法和原始LSTM神经网络架构,具有较高的实用价值.
1 LSTM神经网络
LSTM神经网络是RNN的一个变体,可以有效解决简单RNN的梯度爆炸或消失问题,结构如图1所示.与传统RNN相比,LSTM网络改进[9]主要如下.

图1 LSTM神经网络结构图Fig.1 LSTM neural network
(1) 引入了门控机制控制信息传递的路径,输入门i、遗忘门f和输出门o的状态计算公式为
(1)
式中:σ(·)为Logistic函数;输出区间为(0,1);h为神经网络隐藏层的外部状态;ht-1为上一时刻的隐藏层外部状态;xt为当前时刻的输入;W为状态-输入权重矩阵;U为状态-状态权重矩阵;b为偏置向量;下标i、f和o分别对应相应的门控单元.
(2) 引入一个新的内部状态进行线性的循环信息传递,同时输出信息给隐藏层的内部状态ct和外部状态ht,计算公式为
(2)

上述门控单元中各权重矩阵和隐藏状态ct、ht在训练过程中不断更新,使得LSTM神经网络可以成功学习时序信息中的短期影响和长期规律,实现对未来时刻信息的预测.
2 基于生成式对抗思想的 LSTM改进
2.1 生成式对抗思想
生成式对抗思想的核心思想来源于博弈论的纳什均衡[10],由一个生成器和一个判别器构成,生成器G的目的是尽量学习真实的数据分布,而判别器D的目的是尽量正确判别输入数据来自真实数据还是来自生成器[11].为了取得胜利,需要不断优化,提高各自的生成和判别能力,该过程使用目标函数实现.
minGmaxDV(D,G)=Ex~pdata(x)(lnD(x))+
Ez~pz(z)[ln(1-D(G(z)))]
(3)
式中:E为数据期望;pdata(x)与pz(z)分别为真实数据与生成数据概率分布.
在生成式对抗神经网络中需要首先固定生成器G,让判别器D最大概率地分对训练样本的标签.
maxDV(D,G)=Ex~pdata(x)(lnD(x))+
Ez~pz(z)[ln(1-D(G(z)))]
(4)
随后需要固定判别器D,生成器G通过式(5)最大化D的损失以迷惑判别器,使生成器G的输出与真实数据分布趋于相近.
maxGV(D,G)=Ez~pz(z)[ln(1-D(G(z)))]
(5)
生成式对抗神经网络具有数据增强能力.该思想成功实现了对抗性域适应迁移学习[12]、不平衡样本分类[13]等应用,说明生成式具有对抗神经网络强大的信息归纳与生成能力,也证明了该思想与众多神经网络架构结合的灵活性.
2.2 谱分析方法与波浪频谱特性
海浪及船舶运动通常被视为一种随机性过程,可以利用频谱分析对海浪进行统计意义上的考察.一般将随机过程由时域到频域的变换称为随机过程谱分析,设随机过程的一个样本为x(t),并设其物理含义为波面函数.使用傅里叶变换直接将上述随机过程进行时域与频域上的转换:
(6)
式中:ω为频率.
同时得到谱密度函数:
(7)
式中:T为序列周期.
上述傅里叶变换针对连续函数,实际中由于采样频率不能无穷小,得到的样本往往是有限长的离散数据,所以需要利用离散傅里叶变换方法.采用著名的快速傅里叶(FFT)算法[14]进行时频转换,该方法认为样本x(t)是由N点构成的序列,写作x(n),n=0,1,…,N-1,对应的时频转化式为
(8)
式中:k、n分别为对应于ω、t的离散变量,k=0,1,…,N-1.可借助W因子的周期性和对称性,实现快速时频转换.
波浪起伏和船舶摇荡运动虽是一个随机性过程,但是通过上述频谱分析法可以在统计意义上进行考察分析.PM谱、ITTC双参数谱、JONSWAP 谱等多种可以近似描述波浪谱的表达式[1]也证明了海浪虽然在时域呈现巨大随机性,但是在特定风速下,特定海区的频谱较为稳定.图2为4个机构对北大西洋海区有义波高(Hs)出现概率P(Hs)的统计,该统计说明了在特定海区中特定波高的出现概率一定.
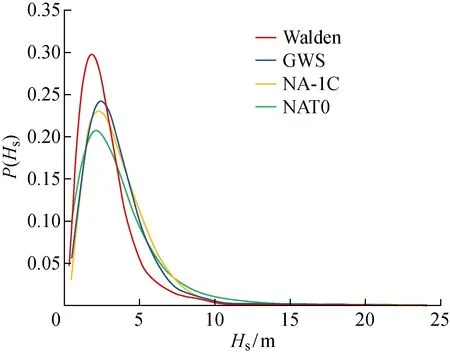
图2 北大西洋波高分布Fig.2 Wave height distribution in the North Atlantic
2.3 融合时频信息的LSTM改进形式
长时间统计得到的特定海区波浪频谱往往呈现相似特征,能够反映波浪的真实分布,其频域特性反映了波浪的重要特征信息,对极短期预报有重要意义.但时频转换难以直接融合至LSTM神经网络框架中.受生成式对抗网络(GAN)中对抗思想的启发,提出GAN-LSTM模型,旨在使用LSTM网络替代生成器,将预报得到的结果和真实数据进行频域转换后输入判别器进行判别,通过判别器使得LSTM神经网络自动学习频谱特征,实现时历特征和频谱特性的双重近似,从而使得LSTM神经网络损失函数最小化的同时实现预报频谱分布接近真实频谱分布,即输出数据的分布逐渐接近真实分布.
LSTM神经网络改进形式实现过程如图3所示,其中虚线框内为GAN中的生成器,生成器得到的频谱曲线由LSTM的输出结果经频谱变换得到,判别器区分生成器频谱分布与真实频谱分布之间差异,并将其直接反馈至LSTM神经网络促使神经网络输出数据的频谱特性能够更接近真实频谱特性.由于训练数据集往往是历史测量数据,数据量较为充足,所以使用训练数据集数据进行频谱变换可以反映特定海区对应的频谱特性,通过上述反馈过程实现频谱信息嵌入LSTM神经网络.在之后的预报过程中,可直接使用经过上述训练过程的LSTM神经网络进行预报,无需额外的频谱特征输入.通过引入GAN思想,成功解决了流式数据无法进行频谱分析的问题,成功将频谱特性融入LSTM神经网络的训练过程中,充分利用了现有信息,成功实现时频耦合预报.
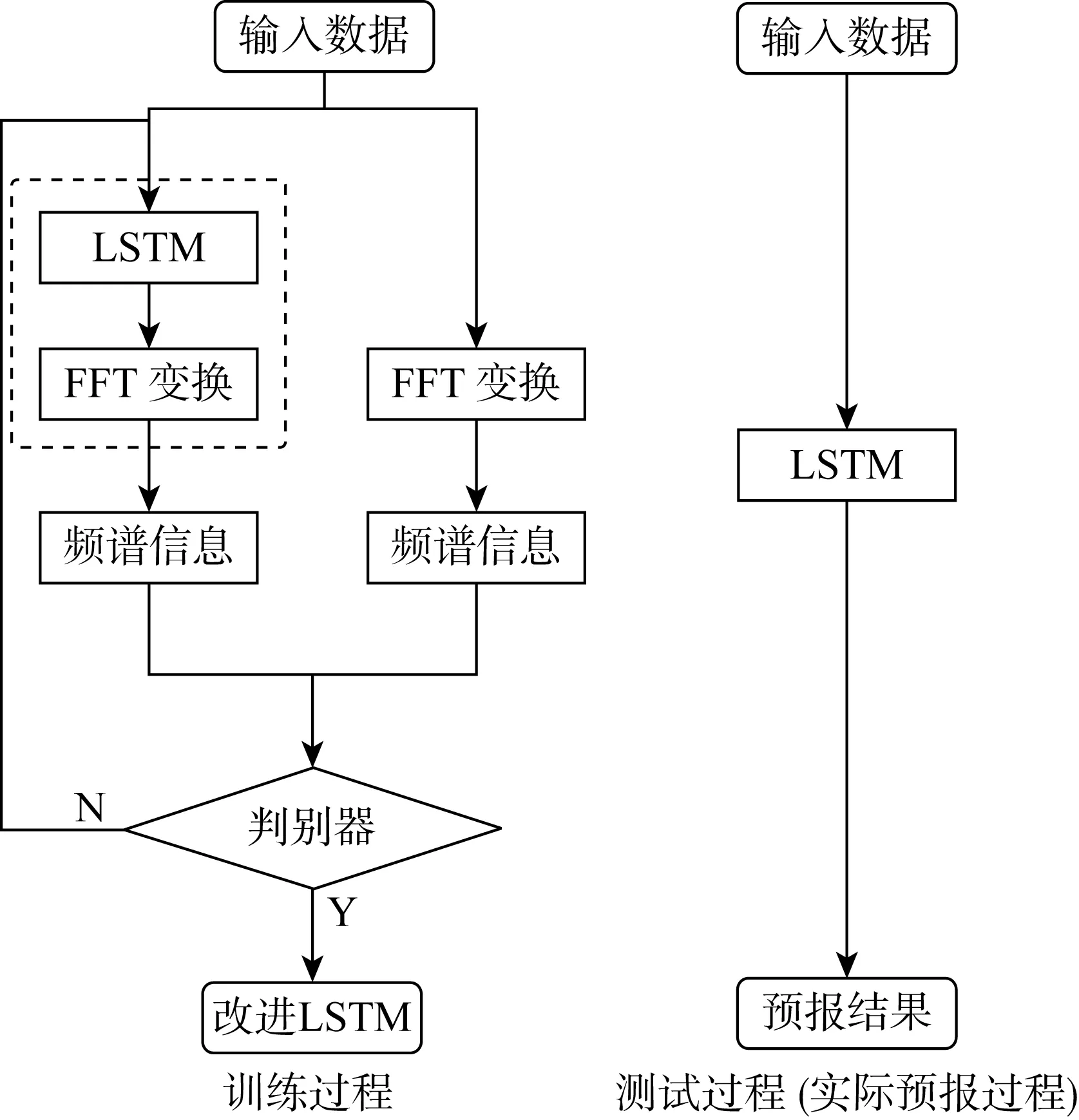
图3 改进的LSTM神经网络流程Fig.3 Flow chart of improved LSTM neural network process
改进的LSTM目标函数为
(9)
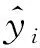
L1通常使用相对熵,又名KL散度表示:
L1=KL(p|q)=H′(p)-H′(p,q)
(10)
H(p,q)=Ez~p(z)(-lnp(z))=
(11)
式中:p为真实分布;q为生成分布;H′为交叉熵函数.
从LSTM神经网络结构的角度来看,本文中LSTM神经网络改进形式在原有LSTM神经网络目标函数中添加了反映频谱近似程度的正则化项L1,实践表明使用正则化项可以在一定程度上减小神经网络输出域空间,使得神经网络可以更快地收敛稳定,并且可以防止神经网络参数过拟合[9].LSTM改进形式的另一个优点为通过对频域特性的学习可以自动抑制输出噪声信息,实现滤波平滑过程.
3 仿真结果与分析
3.1 波高时历数据
数据来自上海船舶运输科学研究所深水拖曳水池某实验.深水拖曳水池长192 m,宽10 m,水深4.2 m;造波机为电液伺服摇板式,最大波高0.3 m,频率范围为0.25~2.00 Hz;浪高仪采用日本进口的四自由度适航仪Gel-430-S及非接触式超声波浪高仪.测量频率为50 Hz,波浪数据时长为240 s左右,共12 158个数据,基本满足训练和测试需要.模型试验与实船之间的缩尺比为λ=50,模型与实船之间满足弗劳德相似关系和斯特劳哈尔相似关系,即对应实际特征周期为λ0.5=7.071倍.
实测得到的波高(H)数据存在系统误差如零飘、随机误差如高频不规则振荡和异常误差如个别点跳点等现象,按照实验规定进行相对应的预处理,预处理后数据如图4所示,其中fr为频率.可知,预处理后数据集中于低频段,分布较为理想.进一步分析数据可知,波高时历中平均周期为0.76 s,最小周期为0.08 s,最大周期为1.84 s.

图4 波高数据时频域特性Fig.4 Time-frequency domain characteristics of wave height data
3.2 模型训练与评价
3.2.1基线模型 为了更准确地说明神经网络方法的优越性,使用传统时序模型作为基线模型进行对照,常见的传统时序模型包括自回归(AR)模型、移动平均(MA)模型、自回归移动平均(ARMA)模型等,具体模型选用根据对波高数据的自相关性和偏相关性分析决定.由图5可知,自相关图像呈现明显“拖尾”现象,偏相关图像呈现“截尾”现象.平稳时间序列的偏相关系数(PACF)为r步截尾, 自相关系数(ACF)逐步衰减而不截尾, 则序列应该选用AR模型[15].因此,基线模型最终决定为AR模型,表达式为

图5 波高数据自相关偏相关分析Fig.5 Auto-correlation and partial-correlation analysis of wave height data

(12)
式中:r为模型阶数;aj为自回归系数;εt为随机扰动项.
实际预报中,往往需要提前多步进行预报从而给后续运动控制等留出充足的决策空间,AR模型无法直接用于多步后预测,需要进行迭代递推,即使用预报得到的Xt作为已知量进一步预测Xt+1,重复该过程直至得到需要的Xt+n结果.
3.2.2LSTM神经网络模型 神经网络模型与传统AR模型的区别在于可以直接建立Xt-p~Xt-1与Xt+n之间的关系,避免了使用递推迭代造成的误差累积.影响LSTM神经网络的超参数众多,使用网格法考察训练数据量、依赖时间步、神经网络隐层数目、隐藏状态数和优化器参数等量对最终预报结果的影响,得到LSTM神经网络模型参数如下:隐藏层数为4,隐藏状态为10,迭代次数为1 200次,依赖时间步为34.优化算法使用Adam算法,其参数lr为0.001、beta_1为0.9、 beta_2为0.99、epsilon为 1×10-8.使用0~100 s上的数据作为训练集,共 5 000 个样本点.
改进LSTM神经网络中LSTM模块同上,区别在于在训练过程中加入判别器模块,判别器为4层的感知机模块,其神经元数目设为[3, 32, 32, 2],神经网络输入参数为频率、幅值和相位,对真实样本的结果标记为1,来自生成器的样本标记为0,目标函数使用交叉熵函数.
3.2.3性能评价指标 上述任务需要使用合适的度量函数对模型的结果进行评价,由于常需要对比多个不同模型之间的优劣,所以性能评价函数应具有一定普适性.常见的性能评价函数包括均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)等,其定义为
(13)

统一使用MSE和MAE对传统时序分析模型、LSTM神经网络模型和改进后的LSTM模型进行评价.使用测试集中100~200 s区间的数据,共 5 000 个样本点.
3.3 仿真结果与分析
分别使用基线方法(AR模型)、LSTM神经网络和改进的LSTM神经网络提前5步(0.1 s)、10步(0.2 s)、15步(0.3 s)、20步(0.4 s)对上述波高时历进行预报,训练数据集使用0~100 s数据,测试数据集使用100 ~200 s数据,性能评价指标使用MSE和MAE,结果如表1所示.

表1 不同工况下预报精度对比Tab.1 Comparison of forecast accuracy under different conditions
由表1可知,在多数工况下LSTM神经网络进行时间序列分析结果明显优于传统时序分析方法,在MSE指标方面,性能提升7%~15%,平均可实现11%左右的提升.改进的LSTM神经网络较基线模型和原有LSTM神经网络的预报精度均有所上升,4种工况下较基线模型性能平均提升16%,较原有神经网络性能提升5%左右,充分证明了改进后神经网络的优越性.部分情况下神经网络预报得到的MAE略大于基线方法,这可能是由于神经网络训练过程中目标评价函数设置导致,属于神经网络中的固有问题.
为了说明3种预测模型的具体效果,随机截取一段时间窗口进行观察.图6为AR模型、LSTM模型与改进LSTM模型预报结果的对比,对应工况为提前预报5步.可知,时间序列分析方法存在一定滞后性,其中AR模型滞后性最明显,且由于误差累积在部分时刻会出现突峰,而使用神经网络方法无需迭代递推,其预测总体上较稳定;神经网络的预报过程中往往会出现偶然的波动(噪声),改进后的LSTM相较于原始LSTM神经网络在一定程度上抑制了噪声分量.

图6 3种模型极短期预报结果(提前预报5步)Fig.6 Short-term forecast results of three models (5 steps in advance)
为了对比分析总体的预测结果,在整个测试集(对应时长100 s)上使用LSTM神经网络与改进LSTM进行预报得到频率特性曲线,对应工况为提前预报15步,如图7所示.

图7 预测结果频率特性曲线(提前预报15步)Fig.7 Frequency characteristic curve of prediction results (15 steps in advance)
以上结果表明,测试集上的频谱特性与图4中整体的频谱特性较为相似,说明大量波浪统计信息对应的频谱存在稳定性,故频率信息可以视为先验信息进行知识迁移用于上文所述的预报过程中.如局部放大图所示,改进LSTM对高频分量起到抑制作用,达到了之前所述平滑滤波效果.本文中按照原始采样频率50 Hz对波高时历直接进行预报,在该采样频率下大量数据位于波峰和波谷之间,可能导致神经网络对波峰和波谷的数据预报能力较差,最终出现1.6~1.8 Hz频率区间内的频谱特性曲线与真实值差别较大的结果,故可进一步探索LSTM和改进LSTM模型在粗粒度预报方面的应用.
4 结论
与图像识别、目标检测等领域不同,波浪和船舶运动对应的频谱往往是稳定的,可以为波浪预报和运动姿态分析提供重要信息.但是频谱信息目前较少地直接应用至现有极短期预报方法中,主要有两方面原因:一方面,目前的神经网络在船舶姿态时序预报领域的应用大多停留在表面,没有与本领域的专业知识进行深度融合;另一方面,频谱分析需要对数据整体进行傅里叶变换,这个方式与极短期预报中数据流式传入、预报结果流式传出的在线预报方式不符,实践中很难将频域信息嵌入其中.受生成式对抗思想的启发,巧妙地将频域信息嵌入LSTM神经网络的训练过程中,提出了GAN-LSTM改进模型,该模型具有以下优点:
(1) 可以充分利用已知信息,实现时频域耦合预报.
(2) 通过学习频域信息,抑制了原有LSTM模型高频噪声分量的输出.
(3) 通过融合频域知识,提高了训练时的收敛速度,并一定程度上提高了神经网络的泛化性.
数值仿真实验表明,上述LSTM改进模型预报精度高,在海浪预测和船舶姿态预报中可以起到重要作用.
