A refined Monte Carlo code for low-energy electron emission from gold material irradiated with sub-keV electrons

Li-Heng Zhou ·Shui-Yan Cao ·Tao Sun ·Yun-Long Wang ·Jun Ma,3

Abstract Considering the significance of low-energy electrons (LEEs; 0-20 eV) in radiobiology, the sensitization potential of gold nanoparticles (AuNPs) as high-flux LEE emitters when irradiated with sub-keV electrons has been suggested.In this study, a track-structure Monte Carlo simulation code using the dielectric theory was developed to simulate the transport of electrons below 50 keV in gold.In this code, modifications, particularly for elastic scattering, are implemented for a more precise description of the LEE emission in secondary electron emission.This code was validated using the secondary electron yield and backscattering coefficient.To ensure dosimetry accuracy, we further verified the code for energy deposition calculations using the Monte Carlo toolkit, Geant4.The development of this code provides a basis for future studies regarding the role of AuNPs in targeted radionuclide radiotherapy.

Keywords Monte Carlo code ·Secondary electron emission ·Low-energy electrons

1 Introduction

The higher radiobiological significance of medium-energy(＜ 100 keV) and low-energy (＜ 20 eV) electrons (LEEs)compared to the commonly used high-energy (＞ 100 keV)electrons has been recently emphasized in radiotherapy.These medium-energy electrons, particularly the sub-keV Auger electrons (20-500 eV), are deposited across a subcellular (＜ 0.5 μm) range in tissue [1] and exhibit a higher linear energy transfer (LET: 4-26 keV/μm [2]) and larger relative biological effectiveness (RBE: 1-20 [3]) than commonly used ～ MeV X/γ-rays (LET: 0.2-2 keV/μm, RBE: 1)in radiotherapy.Thus, similar to heavy-charged particles,this type of electron can induce extreme toxicity in small tumors, clusters of cells, or micrometastases.They also have significant potential for highly targeted implant radiation therapy [4]; however, this is only possible if they are located sufficiently close to the cell nucleus or membrane.More importantly, these nearly non-ionizing LEEs are generally considered less important in radiology owing to the ionization potential (11.7 eV [5]) of liquid water.Following the pioneering work by Sanche et al.[6], several studies[7, 8] have shown that ultralow-energy electrons (LEEs or quasi-free electrons (eqf-): 0-20 eV) can increase the yield of DNA strand breaks.Although certain LEEs are unable to ionize molecules, they can still cause DNA cleavage, such as single-strand breaks (SSBs) and double-strand breaks(DSBs) with a high cross section, via dissociative electron attachment [9].Therefore, a precise description of mediumenergy electrons and LEE transport in certain biological systems is critical.

In targeted radionuclide therapy, radiolabeled high-Znanoparticles, particularly gold nanoparticles (AuNPs), increase the absorbed dose in the near region and enhance the emission of LEEs through interactions with 10-200 keV photons and ～ MeV electrons [10-13].Unfortunately, external beams in radiotherapy, such as photons and electrons, do not penetrate biological tissues beyond the mm and cm scales,respectively [10, 14, 15].This limits the applicability of AuNPs in localized nanoscale radiotherapy.To address this problem, an Auger electron source attached to the AuNPs has been suggested [16] to produce a larger quantity of secondary LEEs from their interactions with gold.These LEEs would have shorter ranges than the initial Auger electrons and further localize radiation energy within approximately 1-10 nm [17, 18].Nevertheless, the influence of AuNPs irradiated with these medium- and low-energy Auger electrons has been rarely studied, and the accuracy of such studies cannot be guaranteed.A recent study [19] found that a stable monolayer film of125I on gold-coated mica substrates amplifies the LEE emission by six times.Owing to the abundant Auger electrons emitted from the decay of125I (23.0 Auger electrons per decay with an average energy of 0.5 keV[20]) bombarding the gold surface, the increase in LEEs was attributed to the secondary electron emission (SEE) from the metal.Previous SEE experiments with a gold foil have shown that primary electrons of 500-750 eV generate the highest secondary electron yield (SEY; the number of true secondary electrons (0-50 eV) emitted per incident electron)of approximately 1.2-1.7 [21-23].Based on these experiments, the potential of LEE therapy combining Auger electron emitters with AuNPs has been suggested [16].Therefore, the primary aim of this study is to build a Monte Carlo simulation code for the transport of sub-keV electrons and LEEs in gold.

In conventional Monte Carlo simulations, electron transportation is processed through the so-called condensed history method, including multiple scattering, single scattering, and continuous slowing down approximation (CSDA)strategies [24].These strategies are effective and fast in macroscopic situations, yet not detailed in describing lowenergy electrons owing to the neglect of the actual electron energy loss in inelastic collisions.More accurate techniques such as energy straggling strategy [24] in material science or track structure strategy [25] for microdosimetry have been developed.These methods require a detailed description of each electron interaction and considers the discrete energy loss during electron transport.There have been various well-developed generic Monte Carlo toolkits, such as Geant4 [26], MCNP [27], JMCT [28], SuperMC [29], and EGSnrc [30], which are suitable for the simulation of many particles.However, most generic Monte Carlo codes use the condensed history method rather than the track-structure method.Recently, track-structure tools or codes, such as Geant4-DNA [31-34], NOREC [35], KURBUC [36], and PART RAC [37], have been implemented to simulate discrete electron transport in liquid water down to several eV.Sakata et al.developed two discrete models called Geant4_DNA_Au_2016 [38] and Geant4_DNA_Au_2018 [39] for electron transport in gold down to 10 eV.An extension of Geant4 MicroElec was also recently developed for microdosimetry and SEE simulations in various materials [40].He et al.[41] developed a Monte Carlo code for low-energy incident electron transport (down to 50 eV) in Al, Ti, Pt,or Au and adopted two strategies, namely the CSDA and track structure.Nevertheless, to study LEE emission from the AuNP surface, Monte Carlo codes considering both LEE emission from the gold surface and the dosimetry accuracy in gold material are essential but remain lacking.

Accordingly, a refined Monte Carlo simulation code for the sub-keV electron transport in nanoscale gold material was developed.This study aims to simulate LEE emission from gold material when irradiated with sub-keV electrons.This would be beneficial for future research regarding the use of AuNPs in targeted radionuclide therapy.In this study, we demonstrate the simulation structure and discuss the physical mechanism and refinements in detail.A truncation method of the elastic cross sections is implemented by considering the Mott theory and electronacoustic phonon scattering theory.In the inelastic calculations, the exchange effect, Born correction, and relativistic effects are simultaneously considered.The initial energy of the Fermi electrons in the conduction band electron excitation was also refined from the Fermi energy to the sampled energy from the joint density of states.The simulated SEE and calculated energy deposition were used to evaluate the reliability of the developed code for lowenergy levels and the accuracy of the LEE emission and dosimetry calculations in future studies.

2 Experimental

The present Monte Carlo code was built for low-energy electron simulations in gold using the energy straggling strategy[24].A comprehensive process for the strategy is described by Tang et al.[42].This method considers the specific electron interactions and individual energy loss in each inelastic event, which increases the accuracy of the secondary electron yield and energy distribution calculation.The low energy limit of the developed code was 0.5 eV above the Fermi level (5.53 eV) of gold.Moreover, bremsstrahlung was not considered, and the reasonably high-energy limit of the code is 100 keV.The basic structure of the simulation is illustrated in Fig.1a.All formulae below are expressed in atomic units.

Fig.1 (Color online) a Schematic diagram of the simulation structure.b Phonon dispersion relations (longitudinal and transverse mode) for Au (circles represent experimental data) [46].c New elastic mean free path (Mott-eph) interpolated from the Mott cross sections and electron-phonon cross sections

2.1 Elastic scattering

The elastic scattering between the incident electrons and the strong nuclear Coulomb field represents the main cause of the angular deflection in the electron trajectory.Owing to the large mass of the nucleus compared to that of the electrons, the energy transfer of electrons during elastic scattering is negligible.In this study, the electron elastic total cross sections and differential cross sections were calculated based on the Mott theory [43] using the ELSEPA code developed by Salvat et al.[44, 45].The muffin-tin radius (1.44 Å) of gold was also considered in the calculation for solid gold.In the latest version of ELSEPA [45], this low-energy limit was extended down to 5 eV.The modification of elastic scattering was introduced by the following electron-acoustic phonon scattering.

At very low energies, electrons tend to behave like Bloch waves rather than as particles [47].Thus, they can interact with the collective movement of atoms in a solid, that is, phonons.We applied the theory for electron-acoustic electron scattering described by Fitting et al.[48] and modified by Verduin [49]and Theulings [50].The electron-acoustic phonon scattering rate is given as follows:

whereεacis the acoustic deformation potential,kBis the Boltzmann constant,Tis the temperature,csis the sound velocity,ρmis the mass density, andA=5EBZis the

wheremDis the effective DOS mass andECBis the energy at the bottom of the conduction band and is equal to 0 for metals.

NBZis the acoustic phonon populationN(k,T) at the Brillouin zone boundary (k=kBZ).The acoustic phonon populationN(k,T) follows the Bose-Einstein distribution.Thus,

whereωBZis the acoustic phonon energyωac(k) at the Brillouin-zone boundary.The acoustic phonon energyωac(k) follows a dispersion relation that was modified to fit the experimental data [46] as follows:

whereαandβare the fitting parameters.There are three acoustic phonon modes: one longitudinal and two transverse.For the longitudinal mode, the chosen parameters arecs=3240 m∕s ,α=3.5×10-8m2∕s , andβ=3.5×10-18m3∕s.On the other hand, the chosen parameters for the transverse modes arecs=1200 m∕s ,α=-7.6×10-8m2∕s , andβ=5.3×10-18m3∕s.The fitted phonon dispersion relations are demonstrated in Fig.1b.

Subsequently, the inverse mean free path (MFP) or macroscopic cross section can be derived by dividing the scattering rate by the electron velocity, which can be expressed ass

In region [EBZ∕4,EBZ], the inverse MFP is interpolated between both values at the upper limit of the top formula and the lower limit of the bottom formula.According to the angular differential scattering rate, the angular differential inverse MFP is given by

The angular distribution of electron-acoustic scattering can also be obtained from the equation above.

Both acoustic phonon emission and absorption exist in electron-acoustic scattering; however, the probability of the former is larger than that of the latter.Therefore, the weighted average energy loss is primarily considered.Although the energy loss is only a few meV, it cannot be neglected in low-energy regions.Thus, the average energy lossEacduring electron-acoustic phonon scattering can be approximated by the following expression:

Finally, the acoustic deformation potential of the metal was derived using the resistivity based on the model of Kieft and Bosch [52].The acoustic deformation potential can then be derived as follows:

whereρRis the resistivity.Using the parameters indicated above, the acoustic deformation potential of gold was found to be 4.86 eV and 1.80 eV for the longitudinal and transverse modes, respectively.

As suggested by Fitting et al.[47, 52], electrons should behave like Bloch waves and interact with phonons at low energies (＜ 100 eV); however, Mott cross sections are no longer valid because the unrealistically high scattering rate leads to a MFP that is shorter than the interatomic distance.Therefore, we modified the elastic scattering as follows: Mott cross sections were applied for energies above 100 eV, whereas electron-acoustic phonon cross sections were used for energies below 50 eV.The elastic cross sections between 50 and 100 eV were derived through interpolation between the two cross sections.As a result, a new elastic MFP is demonstrated in Fig.1c.Although the elastic scattering models may not be sufficient for describing the structure of small AuNPs, a more precise atomic potential for the Mott theory will be obtained in the future using more advanced techniques, such as ab initio and DFT.

2.2 Inelastic scattering

To extend the ELF from the optical limit toq ＞0 , we used the extended Drude model [56] and Mermin model[57].In these two models, the sum of the Drude-type ELFs in (4) is used to fit the optical ELF because both the extended Drude model and Mermin model coincide at the optical limit[58], that is, the Drude-type ELFs:

The fitting model was built based on several previous studies [39, 40, 59, 60].In the development of Geant4 MircoElec, Valentin [60] and Gibaru [40] et al.used a Heaviside step function to cut each oscillator in the fitting.Pablo et al.[61] used an exponential smooth switching function instead of a simple step function for the outer-shell electrons.Based on these prior methodologies, the fitting model is expressed as follows:

For the outer-shell electrons,F(ω) represents a smooth exponential switching function for the electronic excitations[61]:

where Δiandωth.iare the additional fitting parameters.For the inner shells, particularly the K and L shells, which have sharp edges in the optical ELF,F(ω) is chosen as a simple step function Θ(ω-ωth,i).For plasmons and conduction band electrons,F(ω) can be simply set to 1.

The experimental optical ELF, which covers the electron energies from 0.005 eV to 1 MeV, is derived from the databases of Palik [62], Windt [63], and the evaluated photo data library 1997 version (EPDL97 [64]), in which the highenergy optical ELF is calculated using the photo-ionization cross section [65] as follows:

wherenmis the atomic density,cis the speed of light, andσphotis the photoionization cross section.

The fitting results were validated by using two sum rules(f-sum andps-sum) and the mean ionization potential.A partialf-sum rule for the fitted oscillators was also used to distinguish the contribution of the oscillators to the electronic shells.Initial values of the fitting (energy loss from 0 to 100 eV) were partially obtained by referring to the study of Pablo et al.[61].We managed to use 28 oscillators to describe the optical ELF.Figure 2 demonstrates that the fitted ELF data sufficiently agrees with the experimental ELF.

During fitting, the plasmon peak was chosen as 25.42 eV, which is near 24.8 eV in Egerton’s book [66].We verified thef-sum rule of the fitted ELF, that is,Zeff=78.05 (ideal value: 79.0), while theps-sum rule resulted in 1.0908 (ideal value: 1.0).The mean ionization potential based on the fitted ELF was 736.45 eV.These values obtained from the fitted ELF coincide with those from the experimental ELF, with only a small deviation in the high-energy region (L and K shells).This is likely due to the restriction of the Drude functions.If a more accurate experimental ELF is available, then better fitting results can be obtained.We also checked the partialf-sum rule to determine the shell to which the fitted oscillators belong,and the results are also displayed in Fig.2.Therefore,these categorized oscillators enabled the calculation of the inelastic mean free path (IMFP) of the different shells.

The calculation of IMFP is achieved by extrapolating the momentum lossqfrom the optical limit toq ＞0.For the extended Drude model, the extrapolation ofqwas achieved by using the dispersion relation.The extrapolation was performed using the following equation:

Fig.2 (Color online) Comparison of the fitted ELF (solid) and experimental ELF (circles): a contribution of each electronic shell obtained from the combined oscillators at the energy loss range of 0-100 eV; b contribution to all electronic shells of the combined oscillators

Regarding the Mermin model, the extrapolation procedure was already achieved using the Mermin dielectric function [70] as follows:

whereεLis the Lindhard dielectric function [71] andεL(q,0)is the Lindhard dielectric function at the static limit.This is the second inelastic model, which is also labeled as Mermin.

A significant advantage of the extended Drude model and Mermin model is that fitted oscillators can approximate the contribution to particular electronic shells or the plasmon in the calculation.Therefore, combined with the divided shells in the ELF, we can calculate the IMFP of the different electronic shells.

The general calculation of IMFP considering the relativistic high energy correction is performed by

The inelastic cross sections of each shell were individually calculated.For metals such as Au,W-equals zero.As proposed by Pablo et al.[61], the maximum energy lossW+depends on the different electronic shells.Plasmon and 5d electrons are considered collective excitations; thus,W+=E-EF.For the outer-shell and inner-shell electrons,W+equals min[E-EF,(E+Bi)∕2] , whereBiis the binding energy of thei-th electronic shell.The binding energies of the outer- and inner-shell electrons were derived from the FFAST database [73].Meanwhile, a classical Coulomb-field Born correction that accounts for the potential energy gained by the incident electrons is added for the calculation of the outer-shell and inner-shell electrons.This is achieved by replacing the kinetic energyEwithE�=E+2Biin the calculation; however, the energy loss should remain unchanged.

Based on the aforementioned discussion, we compared calculated IMFP with previously reported experimental[74-76] and theoretical data [77-86], which are shown in Fig.3.

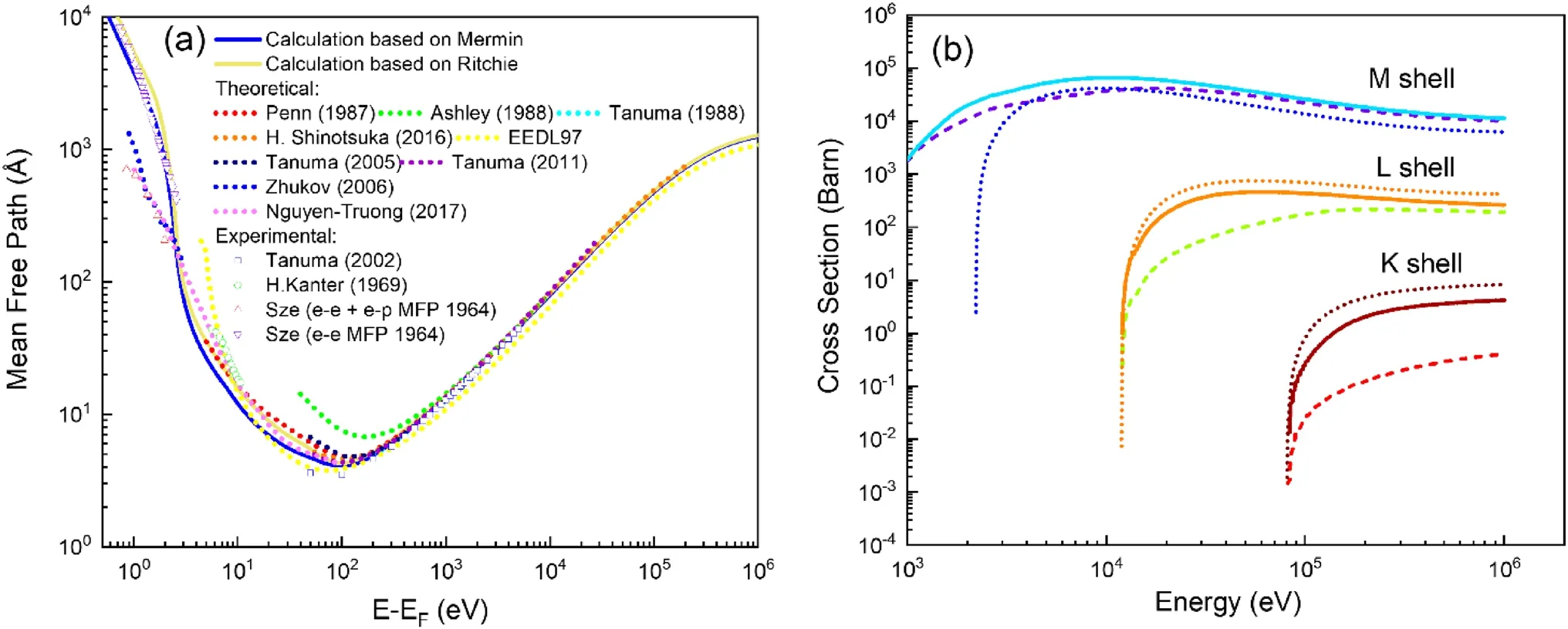
Fig.3 (Color online) a Calculated inelastic mean free path and comparison with other published data [74-76].b Calculated inner shell cross sections (K, L, M shells); solid, dashed, and dotted lines indicate the Ritchie model, Mermin model, and Gryzinski theory, respectively [87, 88]

Figure 3a presents the calculated IMFP, which sufficiently agrees with the experimental and previous theoretical data.A relativistic effect is clearly observed at high energies.At low energies below 100 eV, the modified Ritchie model can derive a good IMFP similar to that of the Mermin model due to its improved estimation of the plasmon lifetime by consideringγas a function ofq.We also calculated the innershell ionization cross sections and compared them with the relativistic Gryzinski’s formula [87, 88] for validation.As shown in Fig.3b, the calculation using the Ritchie model can yield better inner-shell ionization data compared to the Mermin model, which indicates that the Ritchie model is recommended for high-energy electron simulations.This may be due to the fact that for the inner-shells, the plasmonic consideration in the Mermin model is no longer valid, whereas in the Ritchie model, the simple extrapolation ofqwithout considering the plasmon is more applicable.Although the inner shell cross sections using both the Ritchie and Mermin models remain lower than those calculated by the Gryzinski theory, which is considered more accurate, this may be due to the fact that the fitted ELF is insufficiently accurate for the inner shells.Therefore, this lowers the accuracy of the calculated inner-shell cross sections.

2.3 Surface Potential

For an electron to escape from the surface of metals, it must have a kinetic energy larger than the Fermi levelEFand the work functionWF, that is, the potential barrier between the metal surface and vacuum [89].Therefore, the cut-offenergy in the simulation is set toEF+WF, and the electrons are locally terminated below this limit, which can also save memory.

To escape from the surface, once an electron reaches the gold surface, its kinetic energy must satisfy the following condition:

whereEis the energy that considers the Fermi level as the zero point,θis the angle between the electron motion direction and is normal to the surface before its emission, andU=WFis the potential barrier above the Fermi level.Subsequently, according to the quantum theory, the emission will depend on the transmission coefficientT[89-91], which is given by the following:

A random numberRis generated for comparison withTto determine the emission as follows:

The emitted electrons have a kinetic energy ofE-U, and electrons entering the solid will also gain potential energyWFabove the Fermi level.In the SEE simulation, the work function between the gold surface and vacuum was set to 5.1 eV.Considering practical cases of water-gold interfaces for future development, we will use the difference between the work functions of these two materials and assume that the calculation of the transmission coefficient is similar to that considered in the surface-vacuum interface.

3 Results anddiscussion

3.1 Secondary electron emission

3.1.1 Secondary electron yield

To validate the code, we simulated SEE experiments and calculated the secondary electron yield (SEY) and backscattering coefficient (BSC) of gold.This simulation was simply set up as multiple groups of mono-energetic electron beams vertically bombarding an infinite gold plane, and the information of the electrons emitted from the surface was collected.The SEY is defined as the ratio of the number of emitted secondary electrons (＜ 50 eV) to the number of incident primary electrons.The BSC is defined as the ratio of the number of backscattering electrons (＞ 50 eV) to the number of incident primary electrons.To obtain the SEY and BSC, 1 × 106particles were simulated.The uncertainty of this code in the SEE simulation is less than 1%.As presented in Fig.4, we demonstrate the calculated SEY and BSC and compare them with the experimental data collected by Joy et al.[92].Regarding the experimental data, monoenergetic electron beams were used in most of the experiments to bombard the material under vacuum conditions, which was similar to the simulation setup.

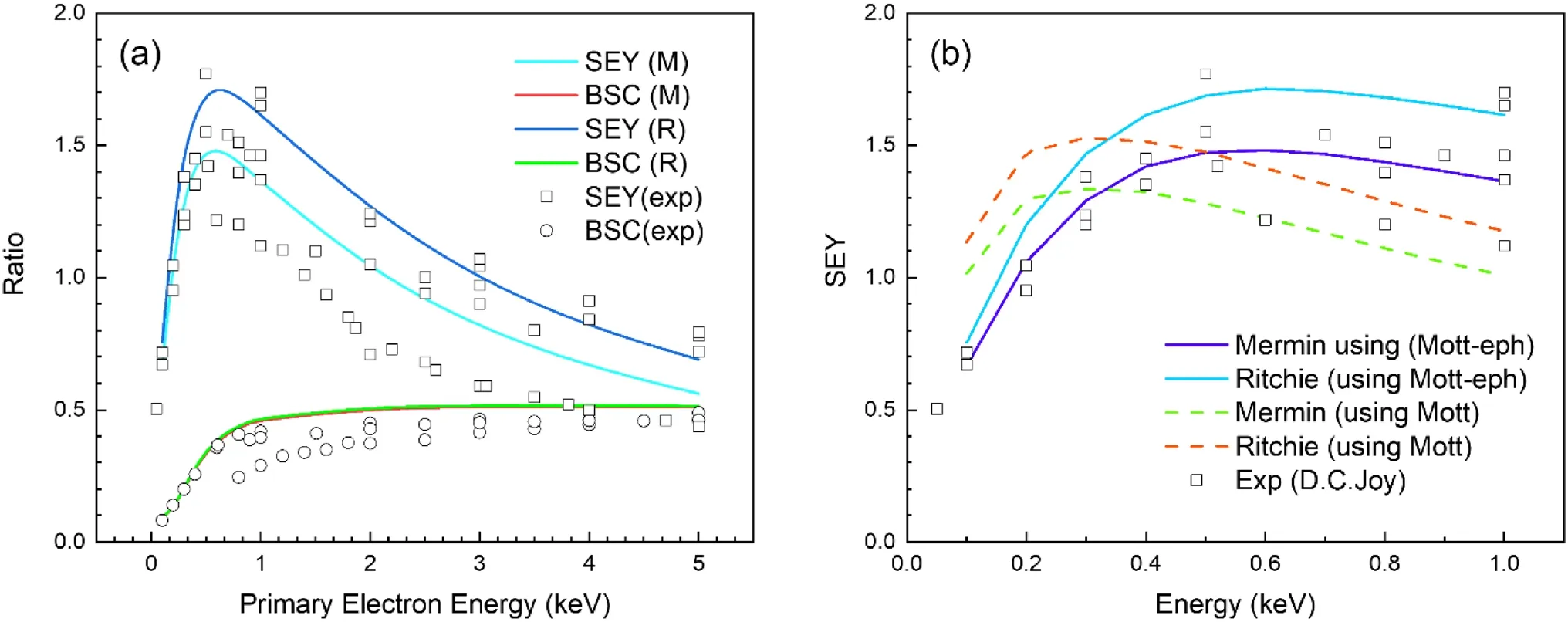
Fig.4 (Color online) a SEY and BSC derived from the SEE simulations and compared to the experimental data [92]; M indicates the Mermin model and R indicates the Ritchie model.b Comparison of the SEY values calculated by two ways (solid lines: Mott-eph, dashed lines: Mott)

As shown in Fig.4a, the simulated SEY values mostly coincide with the experimental values [92], which is essential for the calculation of the emission of LEEs from AuNPs.The Ritchie model derived a larger SEY compared to the Mermin model, whereas the BSC values were similar in both models.In addition, if the modification for low-energy elastic scattering was not added, the SEY values calculated in both ways would mainly differ below 1 keV, as shown in Fig.4b.The figure shows that the calculated SEY using only the Mott cross sections is larger than the experimental values for the primary electrons with a lower energy (＜ 400 eV).The modification of the elastic cross sections improved the description of the SEE.The high SEY also suggests that the125I emitted electrons can enhance the LEE emission from gold nanoparticles.

3.1.2 Secondary electron spectra

The secondary electron spectra are critical for the analysis of LEEs emitted from AuNPs because the cross sections of the LEEs damaging the DNA, such as DSBs and SSBs, are highly energy-dependent [9].The 1 × 107electrons were simulated to obtain stable secondary electron spectra, which are presented in Fig.5.The figure demonstrates that most of the emitted secondary electrons were below 30 eV; a zero-loss elastic peak is also observed herein.

Moreover, the peak of LEEs was found to be located at 2.25-3.25 eV, which is similar to the 2.2 eV peak value reported in the ion-bombardment SEE experiment [93].This large amount of LEE emission also suggests the feasibility of using sub-keV electrons combined with AuNPs as a high-flux LEE source.

3.2 Dosimetry test

Dosimetry testing is critical for the evaluation of further microdosimetry.The stopping power,S(E) , for electrons of energyEcan be calculated using a method similar to the IMFP.The expression forS(E) is shown below:

As shown in Fig.6, we compared the calculated stopping power with those of other theoretical calculations [81, 85,94-97] and experiments [98].The effect of the relativistic corrections introduced in the calculation is demonstrated by the stopping powers at high electron energies, which is in good agreement with the ESTAR [85] and the evaluated electron data library (EEDL) databases [81].With the modifications, the Ritchie model can produce an accurate stopping power comparable to that of the Mermin model at low energies.

The energy deposition was mainly tested using the semiinfinite gold model.Calculation of the energy deposition depth profiles can provide information regarding the energy deposited in gold and its uniformity.This verification also guarantees the correctness of dosimetry for future studies.Electron energy deposition as a function of the depth of semi-infinite gold was calculated for comparison using the developed code and Geant4 standard electromagnetic physics (option 4).In the calculation, 200 eV, 500 eV,1 keV, 2 keV, and 10 keV electrons were simulated; 5 × 106electrons were adopted in each test.The calculated results are shown in Fig.7.

Fig.5 (Color online) Emitted electron spectra from SEE simulations: a 200 eV primary electrons, b 500 eV primary electrons, c 1 keV primary electrons, and d 2 keV primary electrons

The outcomes of both inelastic models in the code present a similar tendency.Figure 7a demonstrates that the ratio of the total energy deposition results of this code to that of Geant4 was approximately 89%-93%.This slight decrease was due to the larger secondary electron emission from the surface.In contrast, the difference in the energy deposition depth profiles is shown in Fig.7b.At low energies, our inelastic cross sections differ from those of the Livermore model (EEDL [81]).Gibaru et al.[40] suggested that the Geant4 standard physics underestimates the range of electrons, which is also observed upon comparing our results.At high energies, the energy deposition depth profiles of both this code and Geant4 tended to coincide.Note that the more detailed energy-straggling strategy in this code is significantly slower than the multiple scattering strategy in Geant4 standard physics.

A function for calculating the energy deposition in the 3D voxels was also added to enable future microdosimetry studies.The method for calculating the energy deposition in the 3D voxels is demonstrated, and the calculation is displayed in Fig.8.The length of the 3D voxels was set to 1 Å, and the maximum length of each axis was 1000 Å.The 1 × 107electrons were simulated here.

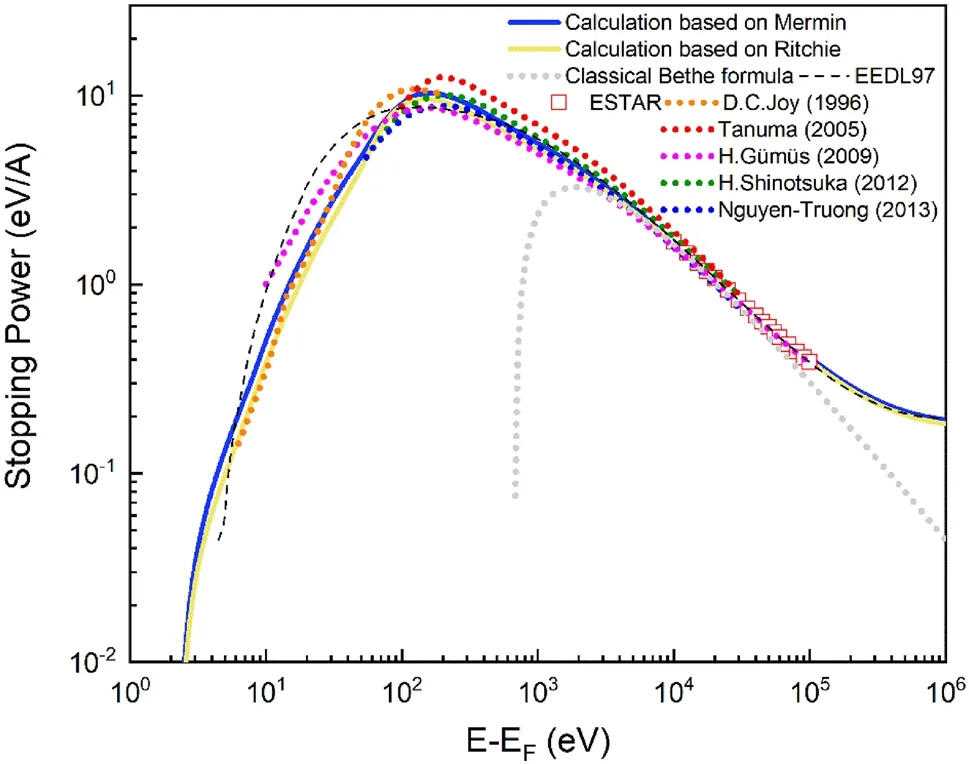
Fig.6 (Color online) Calculated stopping power and comparison with other published data [81, 85, 94-97]

In Fig.8, the spatial distribution of the energy deposition demonstrates good symmetry, which verifies the particle transport in the Monte Carlo procedure.The intensity of the energy deposition in theX-Zplane is more comprehensive than that of the depth profiles.At low energies, the projection of energy deposition in theX-Zplane is an ellipse around the entry point of the electron beams.As the incident electron energy increases, the energy deposition distribution tends to become more cylindrical.The distribution of the energy deposition also demonstrates the nanoscale precision of this code.This function allowed the further visualization and analysis of the electron energy deposition inside the AuNPs when irradiated with electrons.

4 Conclusion

A Monte Carlo code was built to simulate the nanoscale electron transport in gold material down to 0.5 eV above the Fermi level.Mott elastic scattering cross sections were calculated using the ELSEPA code [44].Electron-acoustic phonon cross sections were calculated from the fitted dispersion relation.The elastic cross sections were modified using a truncation method that applies Mott cross sections at energies higher than 100 eV, electron-phonon cross sections at 0-50 eV, and interpolation in between.The optical ELF data were fitted into 28 Drude oscillators, which were categorized into different electronic shells to calculate the cross sections using the dielectric theory.Two inelastic models, the Ritchie and Mermin models, were used to produce inelastic cross sections.The exchange effect,Born correction, and relativistic effects were carefully considered.The initial energy of the Fermi electrons in the conduction band electron excitation was refined from the Fermi energy to the sampled energy from the JDOS.We simulated and compared the SEE results with the experimental results and found a reasonable agreement.The quantum model of the surface potential plays an important role in the calculation of the SEE from the surface.The simulated secondary electron spectra demonstrate a high yield of LEEs from the gold surface when irradiated with keV electrons.Thus, building such a simulation code is significant for studying LEEs in micro- and nanodosimetry.The inelastic stopping power and energy deposition depth profiles were validated.The 3D voxel function was implemented in the developed code to allow further usage.

Fig.7 (Color online) a Calculated total energy deposition.b Calculated energy deposition as a function of depth (1 - 1000 Å with 1 Å as the thickness of each layer) using the developed code (solid and dashed lines indicate the Mermin and Ritchie models, respectively)and Geant4 (dotted line)

This code is planned for the evaluation of the LEE emission in the125I/AuNPs system.It is also being developed for its significant potential in future microdosimetry studies.Further improvements in this code include considering the structure of small AuNPs, implementing the surface plasmon mode for certain AuNPs, adding more materials,and using an advanced geometry intersection algorithm.

Author contributionsAll authors contributed to the study conception and design.Material preparation, data collection and analysis were performed by Li-Heng Zhou, Shui-Yan Cao, Tao Sun, Yun-Long Wang,Jun Ma.The first draft of the manuscript was written by Li-Heng Zhou and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.

Data availability The data that support the findings of this study are openly available in Science Data Bank at https:// www.doi.org/ 10.57760/ scien cedb.j00186.00062 and http:// resol ve.pid21.cn/ 31253.11.scien cedb.j00186.00062.