空间电气间隙与爬电距离包含通过圆弧面的路径时的数学建模与求解
2023-07-04易壮成易俊融
易壮成 易俊融
(1.莱茵技术(上海)有限公司 上海 200072;2.上海交通大学附属中学 上海 200439)
1 原型问题及结构分析
在一块平板绝缘材料(简称板材)上,紫色矩形导体紧贴其正面(上表面),棕色矩形导体紧贴其反面(下表面)。其投影成直角且相交,在板材上有一个离两导体较近的开孔H,位置关系如图1 所示。需要测量两个导体之间通过圆孔H 的电气间隙与爬电距离。电气间隙和爬电距离可统称为绝缘距离。
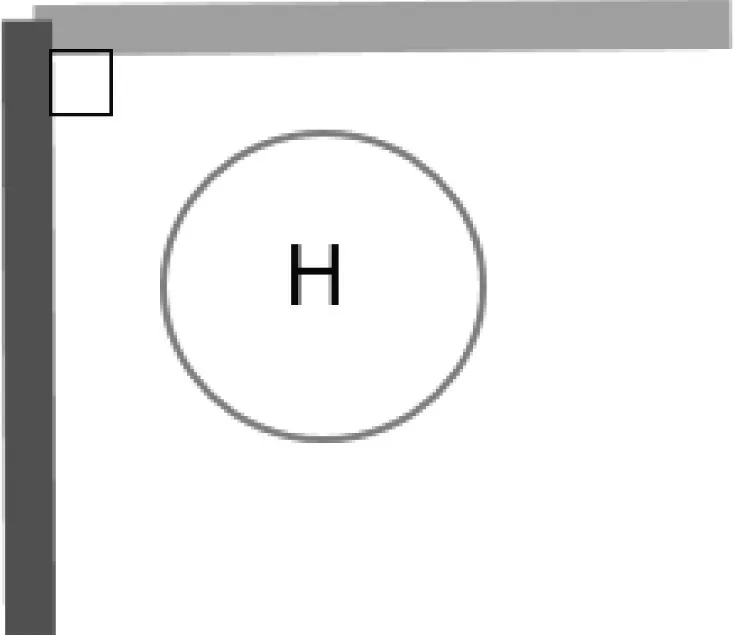
图1 原型结构投影
在本案中,电气间隙是两导体之间通过圆孔的空间最短路径;爬电距离是两导体之间通过圆孔的内表面的最短路径。依此定义,电气间隙和爬电距离的路径都是唯一的。该结构的典型特征是:板材上下表面是平行的,圆孔H的内表面是一个曲面(圆弧面)。我们能够直接测量的参数是H 到两个导体的最短距离。以及H 的直径(d=2r)以及板材的厚度。
显然这个电气间隙与爬电距离是不能直接测量的。但如果我们构造起适当的数学表达式,那么依据定义,电气间隙和爬电距离就成了求对应函数表达式在给定取值范围内的最小值问题。
2 电气间隙的单变量数学模型与结构条件
2.1 数学模型变量的选定
从投影面来分析,假设可能绝缘距离路径的投影交H 左上四分之一圆弧于A, B 两点(显然其他方位不可能距离更短)。设H 的圆心为O,OA 与横轴成α 角(顺时针),OB 与纵轴成β 角(逆时针),如图2。由于A,B 无论处于何位置,都可以分别对正反两面导体边缘(或其投影)作垂线AJ,BK。因此可以确定上表面和下表面的路径必然分别与AJ,BK 平行。
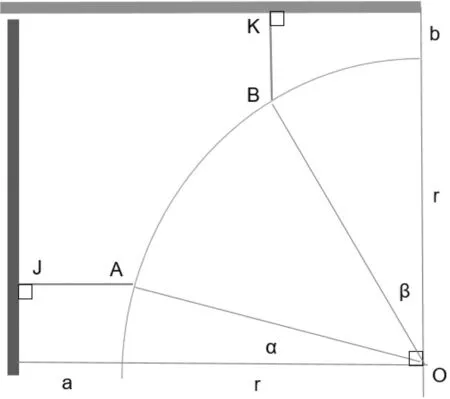
图2 投影面的常量和变量
2.2 角度变量α 与β 之间的关系
假定,路径对应某一个具体的A,B 点,则玄(或弧)AB 长为定值,意味着α+β 也为定值。
设B′,K′是位于板材反面,其投影对应B, K。只需要求得两直线段长度AJ 和B′K′之和的最小值,即可确定绝缘距离的完整路径。定义A,B′为路径在圆弧面上的拐点。
在板材正反两面的绝缘距离路径表达式分别为:
式中:
r —圆孔H 的半径;
a—正面导体与圆孔的最短距离;
α—OA 与最短距离a 所在直线所成的夹角(顺时针);
b—反面导体与圆孔的最短距离;
β—OB与最短距离b所在直线的投影所成的夹角(逆时针)。
由s1+s2=r(2-(cosα+cosβ))+a+b
再依据和差化积公式,
可知,当α+β 为定值(AB 长度为定值时),则α=β 时,cosα+cosβ 最大,s1+s2最小。
2.3 电气间隙的数学模型和EXCEL 计算
由以上可以得出结论,路径取得最小值时,角度α,β 成对称关系。因此可设α=β=x ,这样就可以用单个角度变量 x 来构建数学模型,如图3。
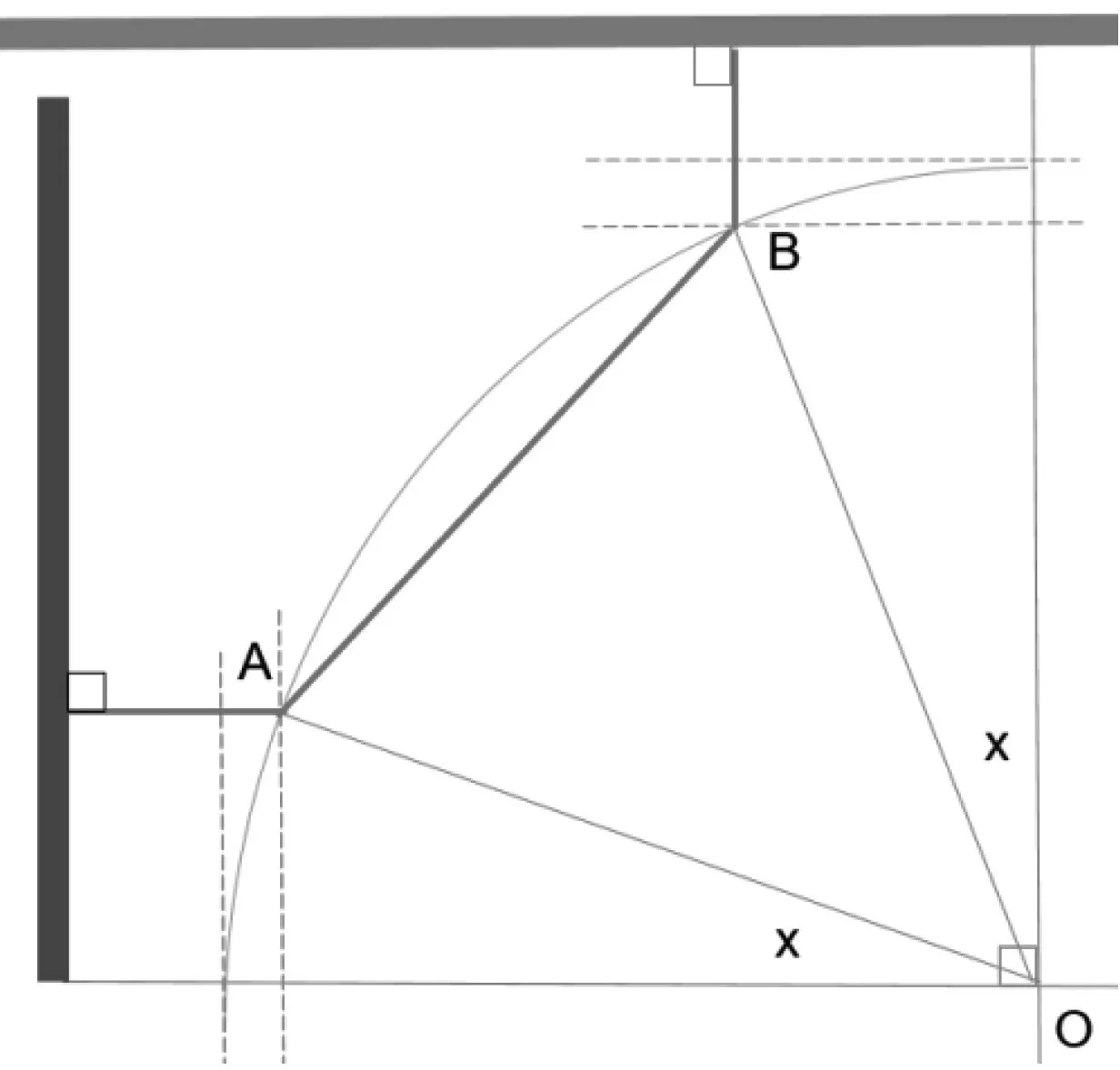
图3 原型结构电气间隙路径的投影
利用余弦定理和勾股定理不难得出通过H 的电气间隙路径s3(AB′)的函数表达式:
式中:
h—圆孔H 的高(板材的厚度);
x—OA,OB 分别与a,b 所在直线所成的夹角。
除非特别注明,相同字符的含义在后续的表述中沿用。
综合以上分析,可得出求解电气间隙路径的完整的函数表达式为:
由于f1(x)是一元函数,在取值范围内(注意原型中x ∈[0,π /4]),可采用EXCEL 表格直接计算筛选而不必求导。极小值f1(x0)就是电气间隙的大小。依据对应的角度x0,即可确定电气间隙路径上所有点的具体位置。
2.4 单变量数学模型成立的结构条件
显然,以上单变量模型成立的数学条件是f1′(x0)=0。结构上表现为极小值点x0所对应的A,B 两点能在导体边缘(或其投影)上找到对应的垂足J,K,不然函数表达式f1(x)不再成立。令集合{α} {β} 分别表示角度α,β 的取值范围,本案中单变量数学模型成立的结构条件是:
x0∈{α},且x0∈{β},
或者表示为:x0∈{α}∩{β};
注意{α}={β}以及两导体垂直都不是单变量数学模型成立的必要条件;只要路径通过圆弧面,该模型也可适用于其他形状的孔。如图4,两个导体成一个已知夹角,只需要调整S3的表达式和x 的取值范围,即可构建单变量数学模型,a 是正面导体延长线与圆弧的最短距离。
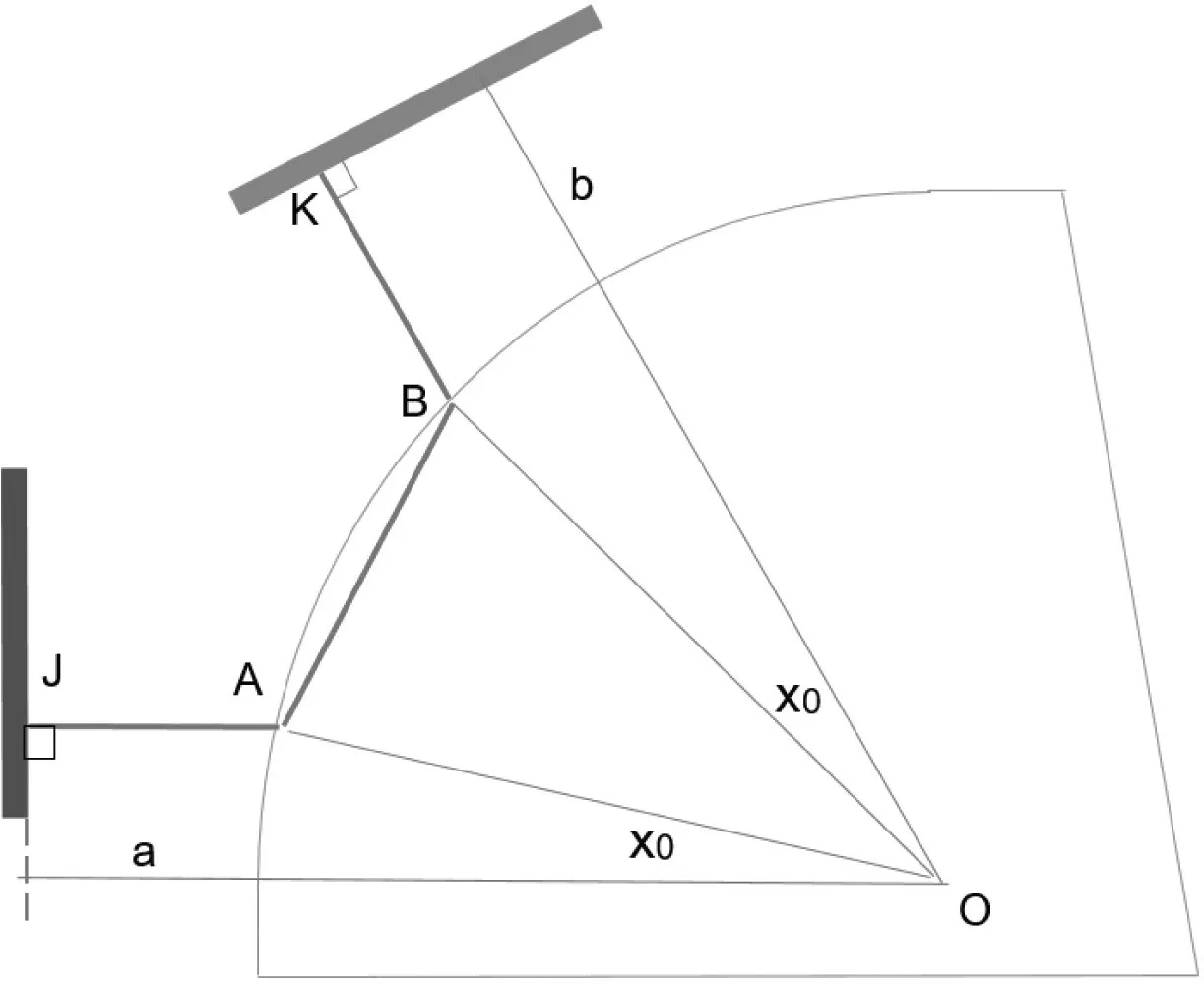
图4 单变量模型的异形结构投影
3 爬电距离的计算方法及其路径的几何意义
3.1 爬电距离的数学模型及其计算
类似地,对于原型结构爬电距离的计算,可以列出对应的数学表达式:
对f2(x)求导数,得:
令f2′(x)=0,则等效于:
由于x< π/4<1.利用正切函数的泰勒展开公式的近似表达式
tan(x)=x+x3/3,
(8)式就变成一个没有二次项的一元三次方程:
利用一元三次方程求根根式可以得出方程的实数解,即爬电距离对应的角度x=θ。f2(θ) 即为本案所求的爬电距离。笔者曾以实例计算过,该近似方程的解足以满足检测实验室对爬电距离的测量精度要求(一般精确到0.1 mm 即可)。
注意计算结果需满足如下数量关系:f2(θ)>f1(x0),且θ>x0。这个结论可以用来检查可能发生的错误。
3.2 原型结构爬电距离路径的几何意义
如果两个异面导体的爬电距离的所有路径都是通过平面表面,则将相关平面翻折到同一平面后画直线即是最短路径 。在本案中,由于有一段路径通过的是一个曲面,不可能直接翻折上下表面。但如果运用微分的思想,可以得出一个有趣的结论。
设爬电距离的路径的投影与圆孔H 的交点为C,D ,D′是该路径与圆孔下表面的实际交点。在C 点做圆弧的切线,切线与线段CM 的夹角也是圆弧CD 与CM 的夹角,记为φ,见图5。可知:
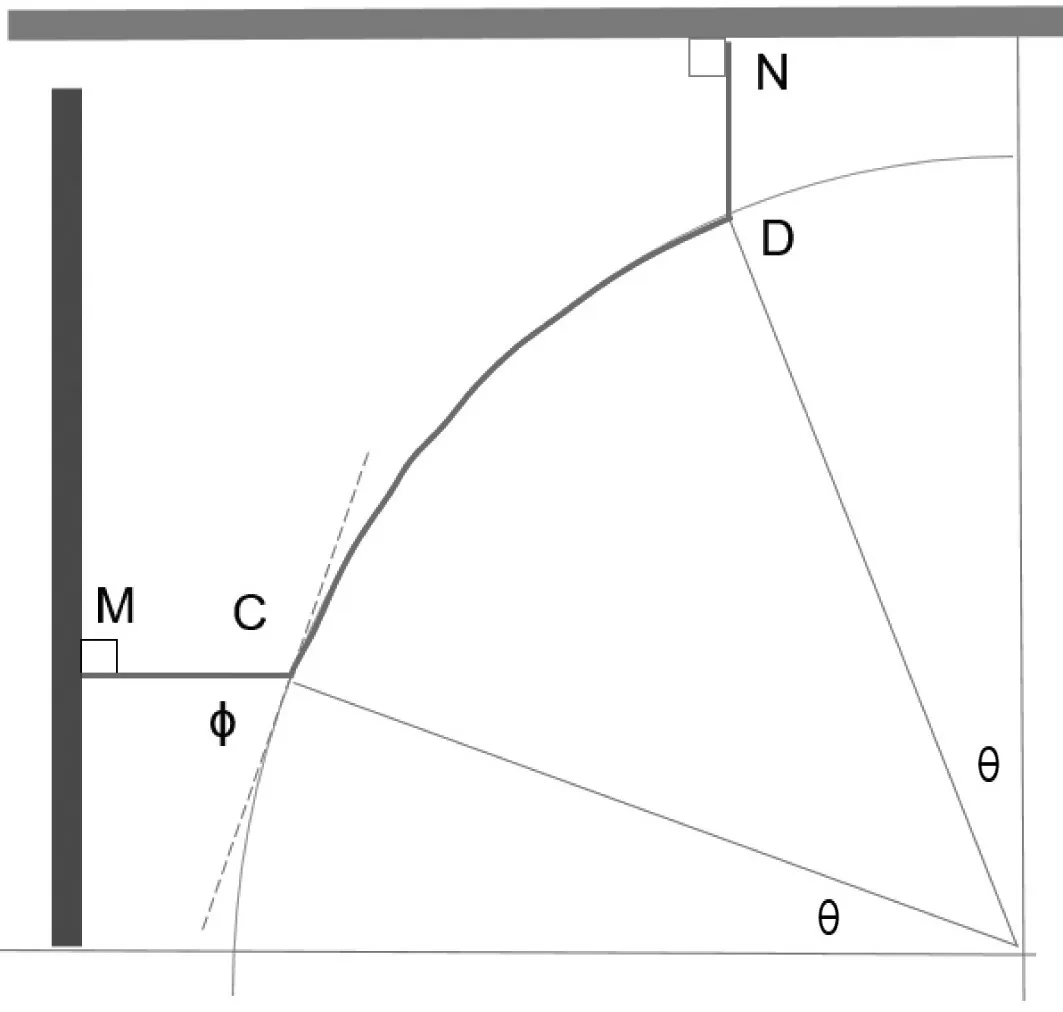
图5 原型结构爬电距离路径的投影
φ+θ=π/2 (10)
将四分之一圆柱侧面沿C 点圆弧切线的方向展开,同时以该切线为轴将CM(可视为无限小平面)翻转到与这个圆柱面展开面到同一个平面上。在这个过程中,线段CM 与弧CD 的夹角φ 一直保持不变。同情的情形也适用于下表面的路径D′N′。
由于θ 满足(8)式,展开后,圆孔H 内表面的爬电距离路径CD′与圆柱体高所在直线正好成θ 角,结合(10)式,可以得出结论,经过上述翻转及展开后,爬电距离上下表面的路径CM 和D′N′与圆孔H 内表面上的路径CD′在同一条直线上,见图6。这与前述平面翻折后的路径取直线有异曲同工之妙。
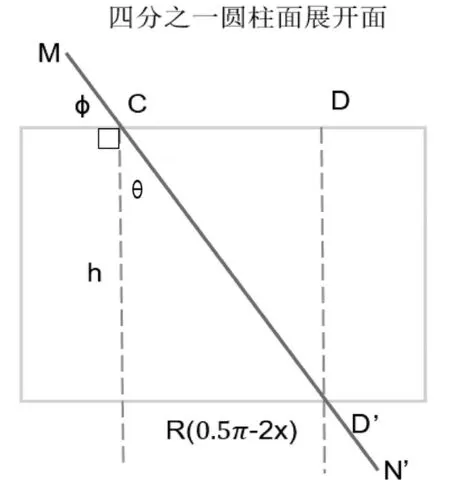
图6 旋转展开后的爬电距离路径
4 电气间隙的二元变量数学(结构)模型及求解
4.1 电气间隙的路径起点为导体端点的数学模型
如图7 所示的结构,不符合2.4 的条件,正面导体上靠近圆弧的端点J 为路径的起点。对于这种结构,需要设两个变量来重新构建数学模型。
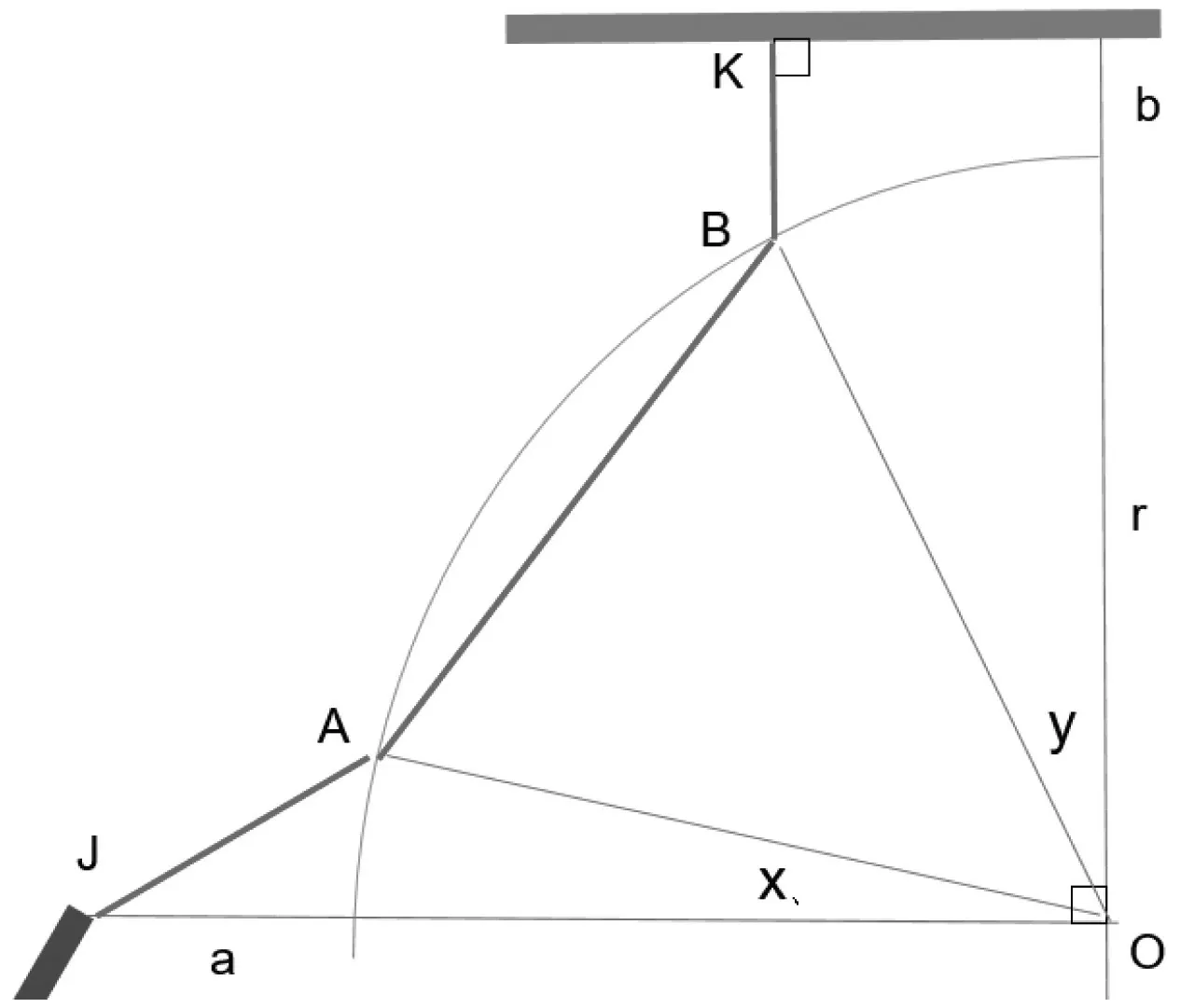
图7 一个导体端点为路径起点的结构投影
不妨设端点J 点正好在横轴上,可列出求解电气间隙路径的二元函数f1(x,y)的表达式为:
式中:
y—OB 与最短距离b 所在直线的投影所成的夹角。
4.2 两元变量函数f1(x,y)极小值的EXCEL 算法推导与确认
把(11)式拆分成三段,分别表达上下表面和圆孔内的路径:
对其求导数h(x)
2)s2(y)= r(1-cos(y))+b
对其求导数:
分别求s3(x,y)对x,y 的偏导数,由于x,y 对其的影响因子相等,其表达式相同:
二元函数的f(x,y)极小值点(x0,y0)一定要满足:
f′x(x0,y0)=0, 且f′y(x0,y0)=0
对应联立(12)和(14)式,以及(13)与(14)式,可知(x0,y0) 必然满足:
因x,y ∈[0,π /2],由(12),(13)知,t 是不小于0 的参数,且(12)和(13)式是单变量函数,给定t 值,即可求取对应(12),(13)两个表达式的反函数的值x(t)与y(t)。再将x,y 带入(15)式,若前后等式成立,即求得最小值对应的点 (x0,y0) 。
4)式两边平方,做简单变形,得:
r2(r+a)2(1-(cos(x))2)=t2(r2+(r+a)2-2r(r+a)cos(x))(16)
看起来复杂的表达式其实是一个关于cos(x)的一元二次方程,利用求根根式,可以求得对应的以t 为变量的表达式cos(x)=g(t)。注意t=0 时,x=0 或者π;x= π明显不合题意,因此对应表达式要省去。从而可以得到(11)式的反函数。
而依据(13)式,可得:
利用EXCEL 表格,第一列为t 值,以0 为起始值,0.01为步进数递增。利用两个反函数计算公式(17)、(18)计算得到第二,第三两列结果;再把第二,第三列结果作为x,y 输入,第四,五列编入(15)式和(11)式,选择第四列结果与第一列输入最接近的一行数据,则求得极小值点f1(x0,y0) 及对应的角度(x0,y0)。从而得出电气间隙的路径和数值。
笔者曾用具体数据进行方法确认,用原始测量数据a=1.50 mm,b=0.70 mm,r=0.90 mm,h=1.44 mm 得出以上(15)、(17)、(18)式及(11)式的具体表达式后,输入EXCEL,得到的解为:
x0=0.277,y0=0.436;f1(x0,y0)=3.96 mm。
在计算过程中,发现第四列数值最接近第一列输入时,对应f1(x,y)最小。且在(x0,y0)附近f1(x,y)的数值变化趋近于0,因此以上方法的正确性和可行性得以确认。
4.3 算法的适用条件
一般地,如果一个绝缘距离的路径可以拆分表达为:
且x,y 对s3(x,y)的影响因子成线性关系,则可以参考4.2 的思路求解。
5 包含桥接的爬电距离路径的二元变量数学(结构)模型示例
当正面紫色导体并未与绝缘板材表面接触,而是与板材表面平行但距离较小,若存在爬电距离桥接,则桥接方向要保证整体路径最小[3]。这里讨论一个典型结构。
设O1是紫色导体端点J 在上表面的投影,连接O1O,以O1O 和圆孔中轴线所在平面作纵向剖面,如图8。以桥接距离X 为直径的球面与上表面交集为圆O1,代表可能桥接路径与上表面交点的轨迹;棕色导体平行于O1O。圆O1的半径R(O1F)是可以直接计算的常数:
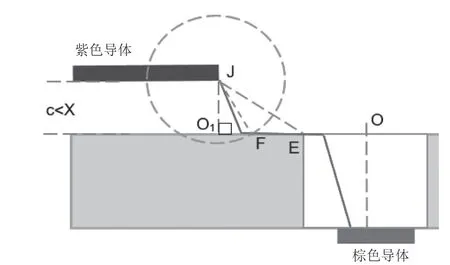
图8 爬电距离包含桥接的结构(剖面)
式中:
X—GB/T 16935.1[1]中 6.2 章节规定的尺寸,即图9所示的JF;
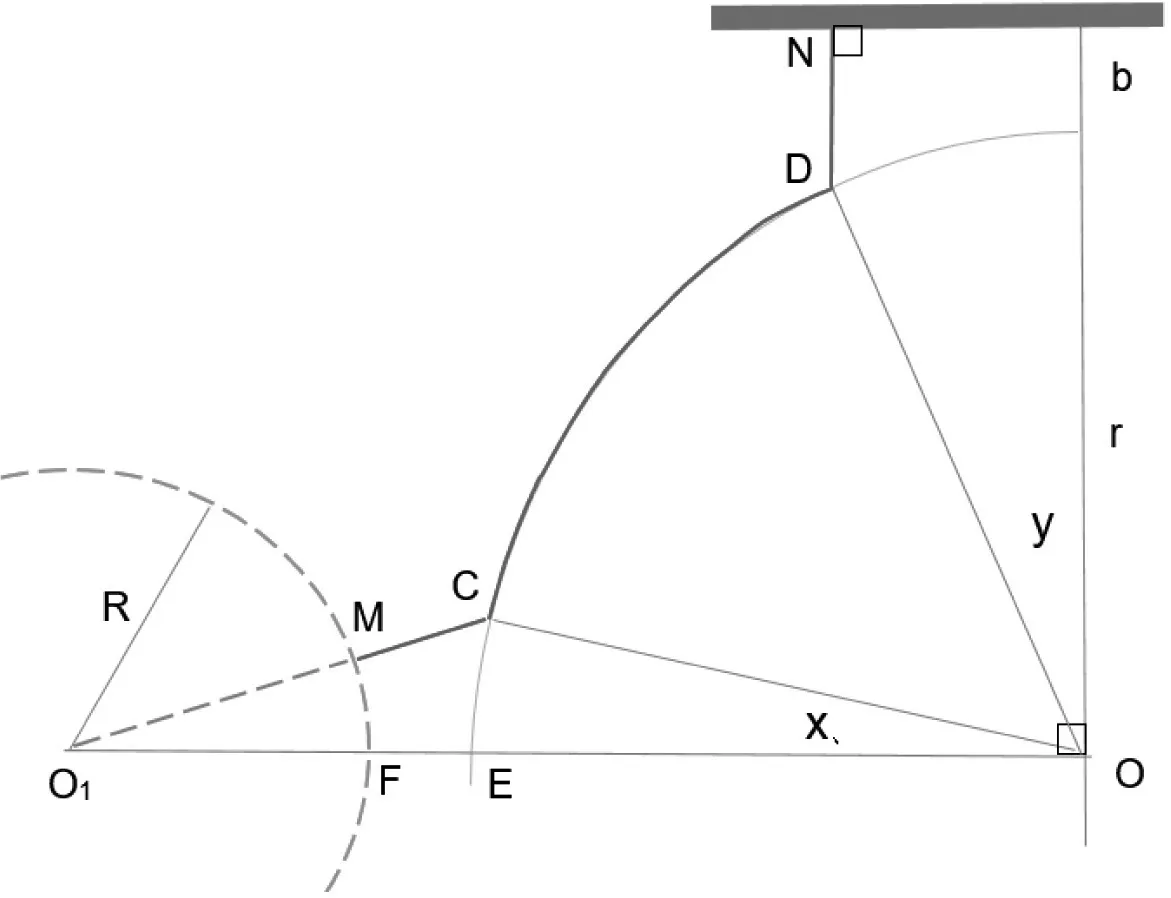
图9 桥接距离方位的确定(投影)
a—紫色导体与上表面距离(直接测量),c<X。
另外,圆心O1到圆弧O 的最短距离也是可以直接计算的常数:
式中:
u —圆心O1到圆弧O 的最短距离O1E;
a—导体端点J 与圆弧O 的最短距离JE(直接测量),a>X。
设路径与上表面圆弧的交点为C。连接O1C, 与圆O1相交于M,对于圆O1上任何异于M 的点M′,必有O1M′+CM′>O1C。因此桥接距离X 必过M 点,如图9。
则紫色导体上表面路径及桥接距离(CM+JM)的表达式为:
式中:
x—OO1与OC 所成的的夹角。
参考3.1,有关爬电距离在圆孔内表面的路径和板材下表面上的路径很方便表达,总路径表达式f2(x,y)符合4.3 的条件。因此该结构模型的爬电距离可求解,具体过程略。
6 结论
综上所述,测量通过空间曲面结构(如圆弧面)的电气间隙和爬电距离时,需要先利用曲面上路径拐点的几何特征定义变量以建立简明的数学模型,并判断结构是否符合模型成立的条件。对于必须建立二元变量数学模型的结构,还需要运用数学工具推导出算法,再辅以EXCEL 求解出正确的路径。对于爬电距离存在桥接的情况,应先确定桥接距离的方位。以上探讨可做为检测实验室的能力验证和日常测量参考;对从事有关产品结构设计的研发人员也有借鉴意义。
