基于电机系统模态仿真分析的换相噪声正向设计研究
2023-07-04刘志华赖泽丰胡佳伟谢开元
刘志华 陈 成 赖泽丰 胡佳伟 谢开元
(珠海格力电器股份有限公司 珠海 519070)
引言
直流电机的永磁转子可以消除铜耗和铁耗,使其具备效率高且转速范围广的特点,因而在一些电器特别是空调器中得到广泛应用,空调内风机的电机大多选择直流电机,电机部件的噪声水平直接影响到用户对空调器声品质的评价,故直流电机的噪声便受到了空调器设计人员的重点关注。针对换相噪声产生的原理进行分析,并从机械振动的角度提出了抑制换相噪声的方法[1],其中永磁直流电机的低频噪声为电机换向噪声,高频噪声为径向电磁噪声,可以从减振的角度提出具有一定可行性的改善措施[2],行业内通常采用局部屏蔽法、声压法、频谱法对系统的空调器进行噪声源识别和传递路径分析,通过对不同阶次的噪声进行分析确定其声源[3]。在类似空调、油烟机等产品上换相噪声的优化方法通常从风机系统和电机的结构及匹配上寻求解决方案[4],但缺乏结合理论模态计算方法和试验模态分析方法对系统进行动态特性研究[5],将试验与仿真在模态分析上的联合应用可更加有效的解决问题[6]。直流电机存在一固有特性,即工作时伴随换相转矩脉动,在特定条件下就会与电机系统发生共振从而引起明显的低频换相噪声。直流电机换相噪声的控制与优化在空调器设计阶段就应该进行,本文针对直流电机换相噪声产生的原理与试验测试相结合,基于电机系统的模态仿真,提出空调器直流电机换相噪声的正向设计。
1 直流电机换相噪声机理
1.1 直流电机的工作原理
常见的无刷直流电机结构简单,由电机定子绕组、电机永磁转子、功率驱动电路(即电子换相电路)和转子位置传感器构成。
以FG60A-ZL 电机为例简易说明直流电机的工作原理,该电机为8 级12 槽电机,在电机运行的某一时刻,定子与转子的位置关系如图1 所示,取出该电机的一个单元电机(即定转子各一对极)进行简化分析,电机通过电子换相电路向电机定子绕组供电,转子每转动一个角度,电机转子位置传感器检测并提供信号去触发功率开关晶体管使之导通或截止,使得电机定子绕组依次改变通电状态,如此某些原本没有电流的绕组开始流通电流,某些原本有电流的绕组开始断开电流或电流方向改变,从而迫使定子绕组的磁状体形成规律性变化,电机的各相绕组按一定顺序工作,从而控制电机转动。

图1 电机结构及工作原理示意图
1.2 直流电机的换相转矩脉动
一个单元电机在一个周期内会有六种工作状态(如图2 所示),当相邻两种工作状态进行转换时,由于其相电感的存在导致了电流在换相过程中无法突变,便会在定转子之间产生不平衡电磁力,延时产生的不平衡电磁力使转子在转动时出现转矩脉动即换相转矩脉动作用于电机的定、转子。
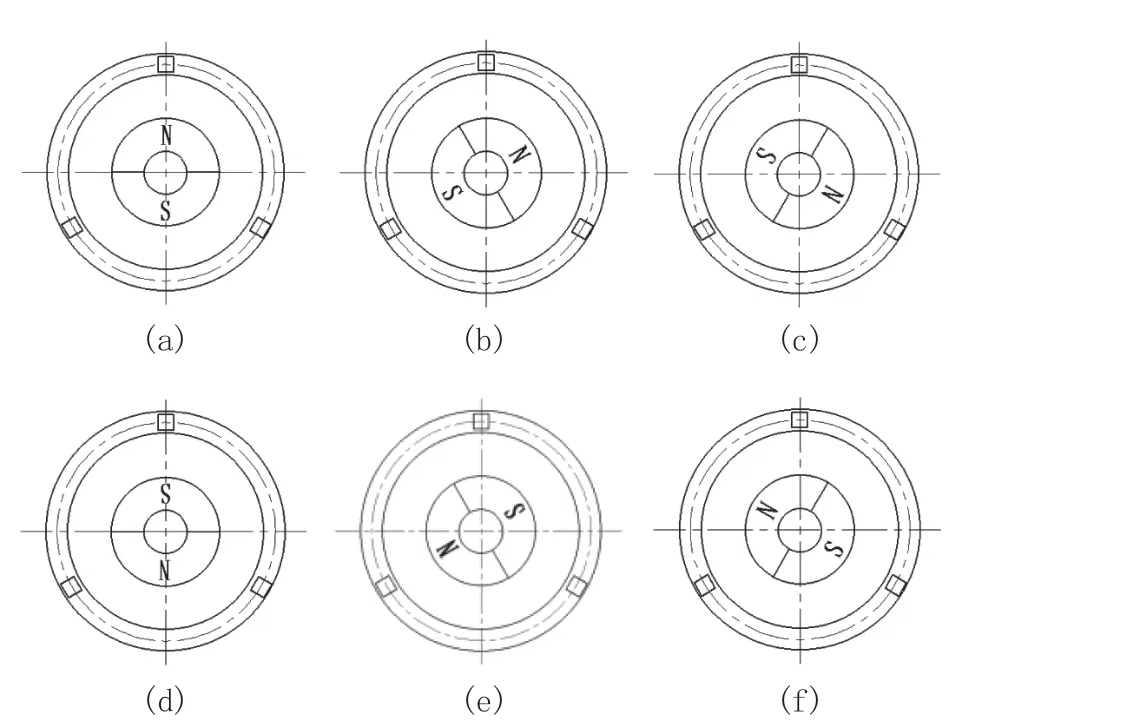
图2 单元电机在一个周期内工作状态
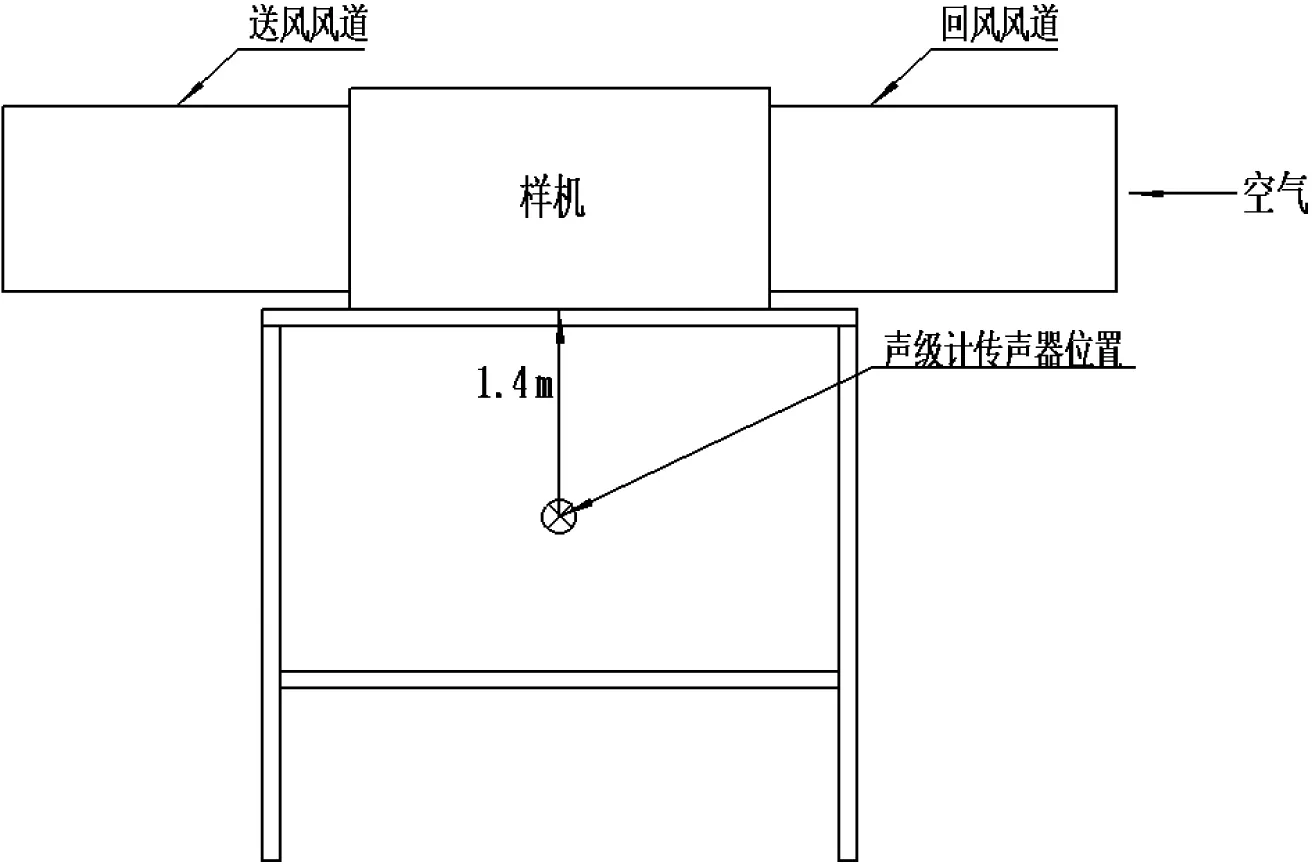
图3 噪声测点示意图
直流电机换相转矩脉动的频率为:
式中:
f—换相噪声频率(Hz);
i—频率的阶数;
m—电机定转子中每对极在一个周期内所对应的工作状态数;
p—电机极对数;
n—电机转速(rpm)。
对于FG60A 这类8 级12 槽的电机具有4 对上述单元电机即4 对极,故一个周期内的工作状态就存在24 种,由此可以简化换相转矩脉动频率即换相频率为f=0.4×n。
2 空调异常噪声的测试及分析
搭载FG60A-ZL 电机的某型号风管内机,低档运行时存在明显的“呜呜”声异响且持续时间较长,使用听诊器识别,该异响从电机中传出,初步判定为上述直流电机的换相噪声。我们对该型号样机制定噪声及振动的测试方案,对该异响进行测试分析。
2.1 整机噪声测试及频谱分析
采用Head 公司的多通道信号采集系统在半消声室中进行噪声测试,机组放置于2 m 高的测试架上,且送风口、回风口接风管,并调节至额定静压,传声器摆放于机组正下方1.4 m 处,对机组送风模式下的各档位噪声信号进行采集。
噪声数据如表1 所示,很明显各档位的噪声总值相差不大,但是低档的噪声峰值高达23.1 dB,明显高于其余两个档位的噪声峰值,低档噪声频谱如图4 所示,噪声峰值频率为368 Hz,与电机低档转速920 rpm 所对应的换相频率f=0.4×920=368 Hz 一致,可以初步判定该机组低档时的“呜呜”声异响为直流电机的换相噪声。
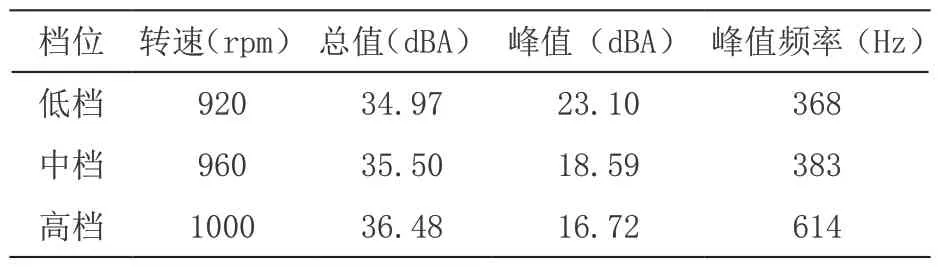
表1 各档位下噪声数据
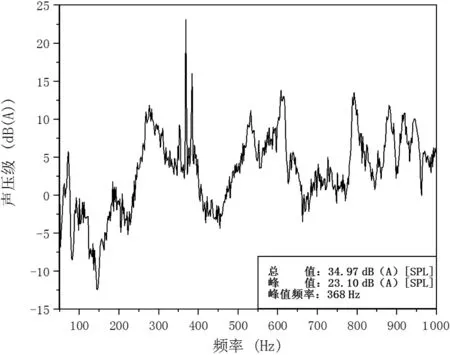
图4 机组送风模式低档运行噪声频谱
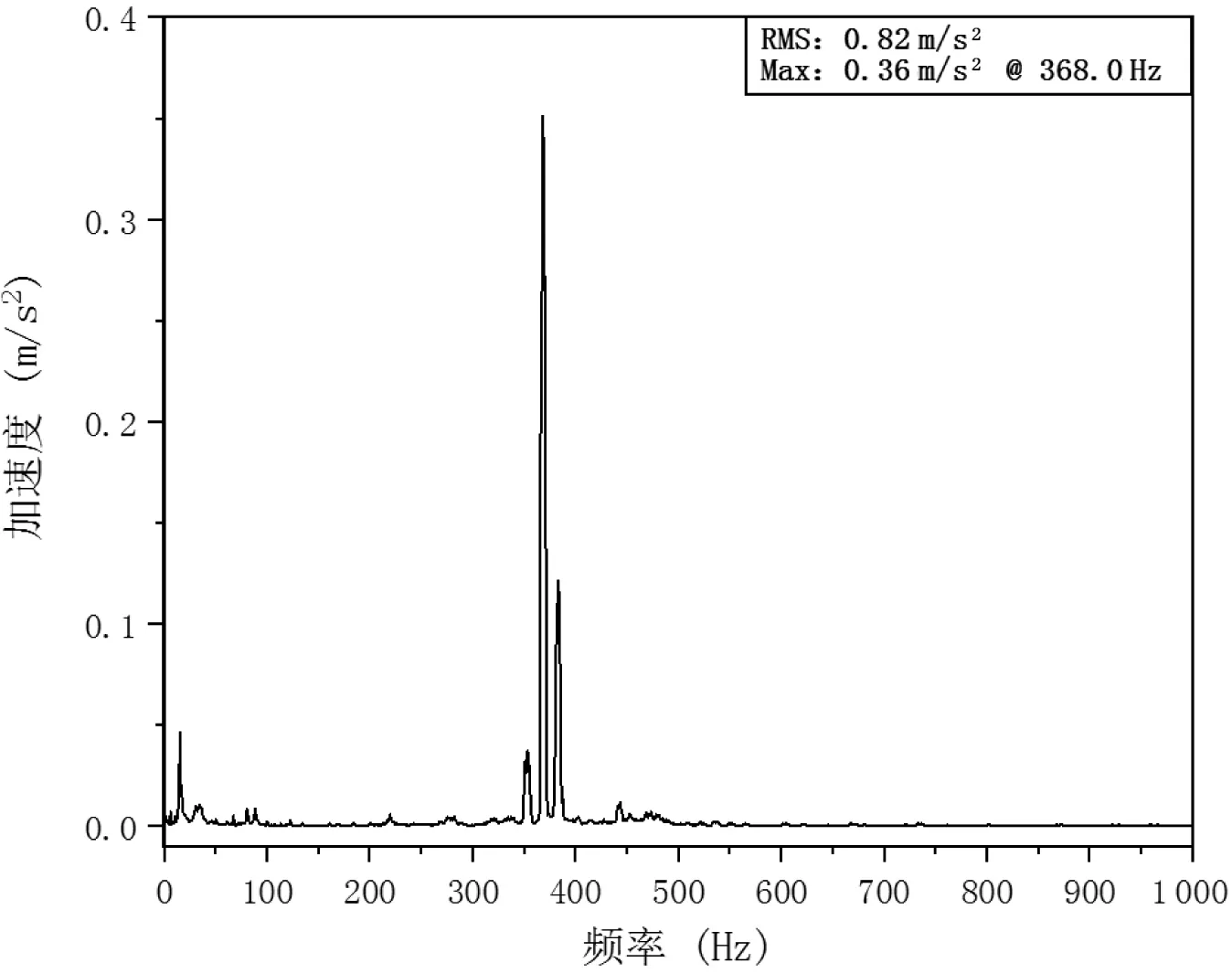
图5 机组送风模式低档运行电机轴向加速度振动频谱
2.2 电机振动测试
采用LMS 多通道信号采集分析设备、PCB 压电式三相振动加速度传感器在送风模式下对电机各档位的振动信号进行采集,测点布置于电机壳体中间位置。电机各档位的振动加速度峰值如表2 所示,从表中可明显得到,电机在低档运行时,电机的轴向加速度峰值会高出许多,所以判断低档的轴向振动存在异常,取低档轴向振动频谱分析。
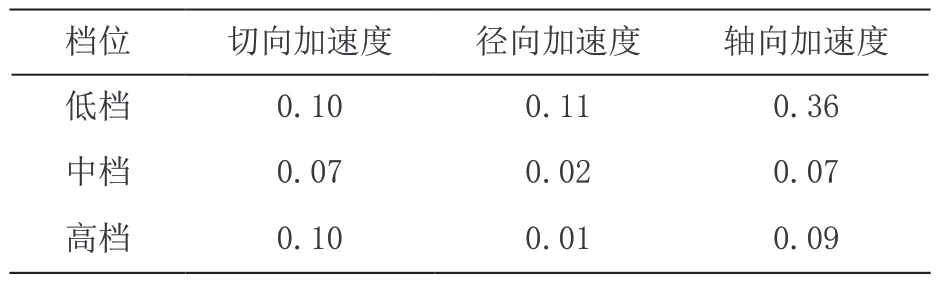
表2 各档位下振动数据(m/s2)
从频谱中可知,机组低档运行时,电机轴向振动加速度存在明显异常峰值高达0.36 m/s2,且其峰值频率为368.0 Hz,与电机低档转速920 rpm 所对应的换相频率一致,故可以判定该机组低档运行时出现的异响噪声是电机异常振动引起电机系统共振所致。
3 电机系统模态分析及实验
进一步确定导致机组产生换相噪声的固有频率与振型,需要对电机系统进行模态计算,采用有限元法对电机系统进行模态分析,并进行试验验证。
电机系统的核心部件为电机与风叶,因为电机内部结构比较复杂,而且电机的模态主要体现于电机轴上,所以在模型简化时将电机简化为一个实体,对简化后的电机-风叶轴套-风叶这个电机系统进行网格划分,建立有限元模型,电机、风叶和风叶轴套采用1.5 mm 四面体网格进行划分如图6 所示,各部件的单元类型及单元尺寸见表3。再通过表3 所示的参数定义各零部件的材料属性,计算电机系统在自由状态下的固有频率与振型,由于该机组换相噪声的峰值频率在368 Hz,故需要重点关注电机系统500 Hz 以下的模态。

表3 电机系统部件材料参数

图6 电机系统有限元模型
对电机系统进行模态测试(如图7 所示),从而验证理论模态计算的准确性,在与仿真计算相同的边界条件下,试验采用锤击法对电机系统进行模态测试,使用PCB 冲击力锤进行激励、PCB 压电式振动传感器、LMS振动噪声测试系统进行信号采集和分析,提取电机系统的测试模态。

图7 电机系统模态测试
仿真计算与测试所得模态固有频率和振型对比如表4 和图8 所示。
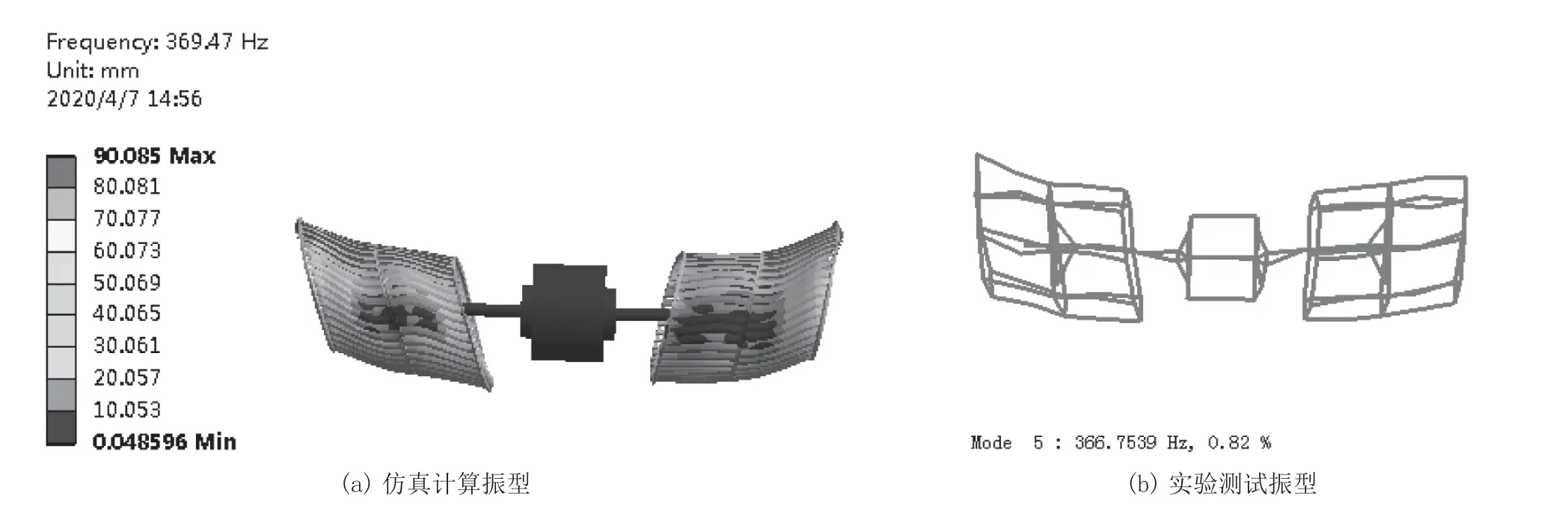
图8 仿真计算与试验测试振型对比(第4 阶模态振型)

图9 结构更改后模态仿真结果
从表4 可以得出,仿真计算的得出的固有频率与测试得到的固有频率趋势相同,数值相近,最大误差为9.69 %,平均误差在4.53 %以内。仿真计算与测试均得到了与机组换相噪声峰值频率相近的固有频率369.47 Hz和366.754 Hz,且从图8 可以明显看出仿真计算与测试所得的该阶模态振型基本一致。
综上,电机系统的振动模态仿真计算与试验测试基本吻合,确定了导致机组产生换相噪声的电机系统固有频率为366.754 Hz、振型为图8 所示,并且验证了上述仿真计算方法的有效性。
4 电机系统的优化设计
4.1 基于模态仿真的电机系统结构优化
为了解决该电机在低档时的换相噪声问题,对电机系统的结构优化,然后再对优化后的电机系统进行模态仿真,直至仿真预测换相转速点明显偏离电机低档转速。
从仿真及模态测试结果可以得出,系统的模态大多表现于风叶负载上,故结构优化选取风叶为对象,针对风叶的易更改参数(如风叶的材料)进行优化,实现负载结构优化。通过改变风叶的玻纤比更改负载的质量,从而优化电机系统的模态。
如表5 所示,风叶原始玻纤比为5 %,通过更改其玻纤比至10 %和15 %,对风叶的结构属性进行优化,模态仿真预测的问题转速均出现了偏移。负载10 %玻纤比,电机系统模态计算得到的问题转速为945 rpm,与低档转速相差20 rpm 左右,理论上可以有效避免该转速下的换相噪声问题;负载15 %玻纤比,电机系统模态计算得到的问题转速为961 rpm,虽然与低档转速相差近40 rpm,可以避免低档出现换相噪声,但是机组中档运行转速为960 rpm,故该状态下机组中档会存在共振风险。
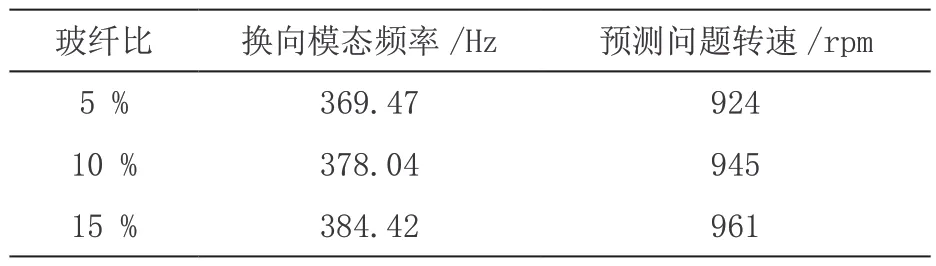
表5 风叶玻纤比及其系统模态仿真结果
综上我们将该机组风叶负载玻纤比由原始的5 %更改为10 %,对结构优化后的机组进行噪声测试,测试结果如表6 所示。
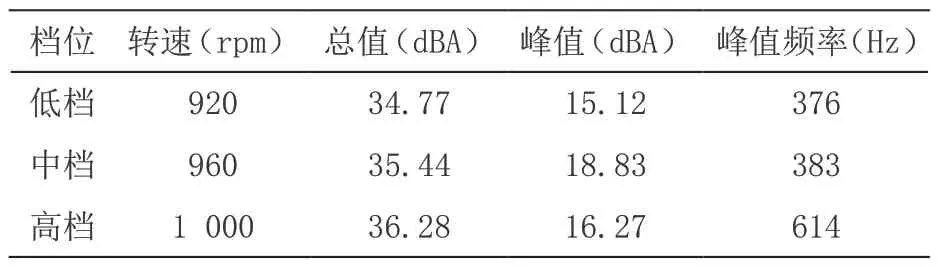
表6 结构优化后各档位噪声数据
由表6 和图10 可以明显看出,在结构优化后机组低档噪声峰值明显降低,且低档噪声峰值频率也不再是低档转速电机所对应的换相频率,即该机组低档换相噪声问题已解决。经上述试验验证,通过对结构整改后的电机系统进行模态仿真,实现了机组模态的优化,进而消除了既定转速下的换相噪声。
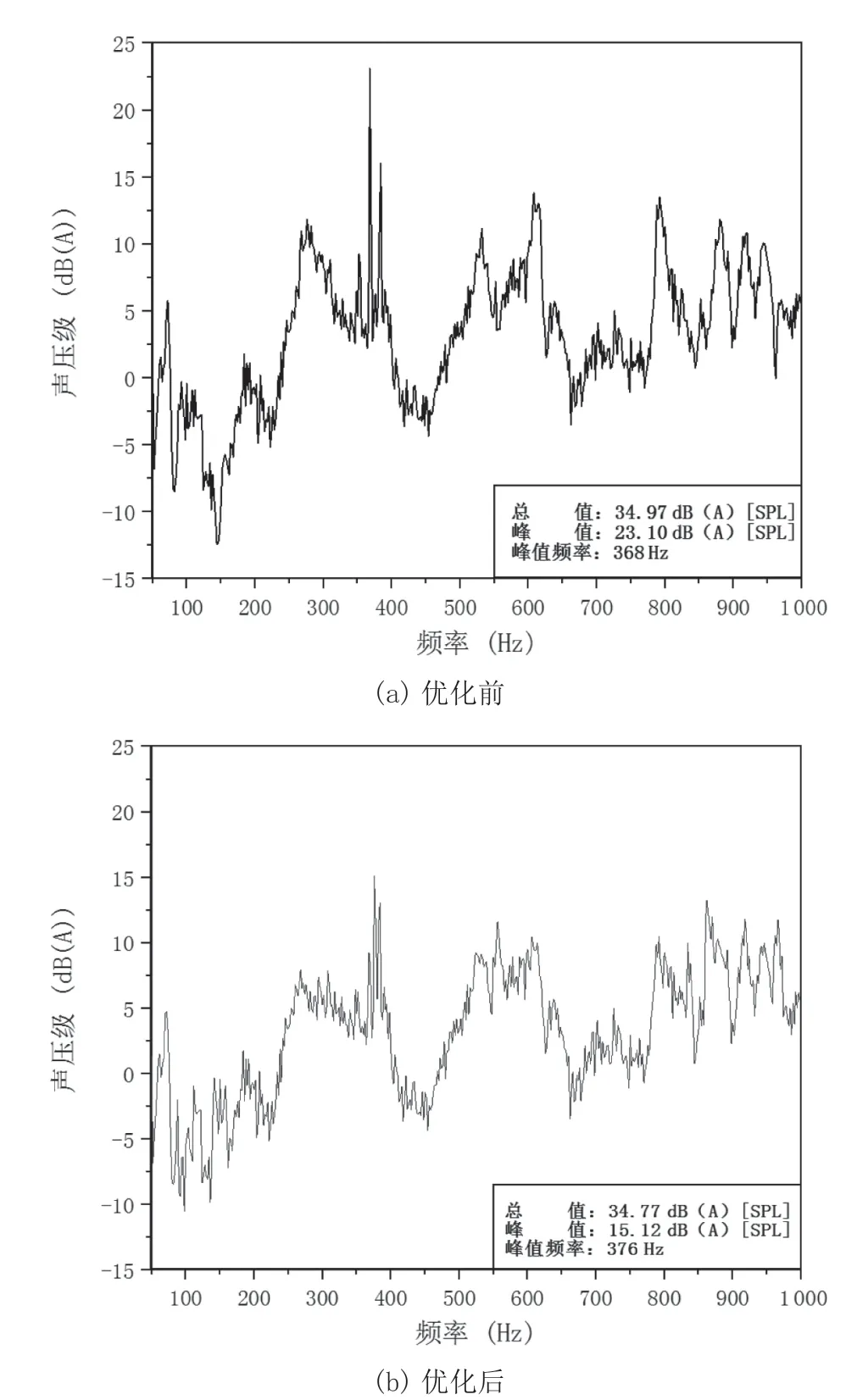
图10 机组送风模式低档运行优化前后噪声频谱对比
5 结语
本文针对直流电机换相噪声产生的原理同实验测试相结合发现:
1)直流电机换相噪声产生的条件为电机的换相转矩脉动与电机系统某阶特定的模态发生共振。
2)空调机组异常噪声峰值频率、电机振动加速度峰值频率与其档位运行转速所对应的换相频率一致,该异响噪声为换相噪声,所以机组电机系统一定存在与换相频率相近的模态频率点。
3)通过电机系统模态仿真,可以得到电机系统的换相模态振型,同时模态测试结果也验证了可以通过模态仿真对换相频率点进行预测,结合需要使用的转速并通过结构更改避开换相模态频率点,实现空调器直流电机换相噪声正向设计。
