扩散段中心轴偏移距离对非对称文丘里施肥器吸肥性能的影响
2023-07-04胡贵荣李诗莹金嫣婧王振华刘宁宁
胡贵荣,李诗莹,金嫣婧,曹 缘,王振华*,刘宁宁
(1.石河子大学 水利建筑工程学院,新疆 石河子 832000;2.现代节水灌溉兵团重点实验室,新疆 石河子 832000;3.兵团工业技术研究院,新疆 石河子 832000;4.农业农村部西北绿洲节水农业重点实验室,新疆 石河子 832000)
0 引 言1
【研究意义】中国是农业和人口大国,水肥一体化技术的应用对保障中国粮食安全具有重要作用[1-3]。施肥设备是水肥一体化技术的核心装备之一,目前最常用的施肥设备包括压差施肥罐、智能水肥一体机、文丘里施肥器、比例施肥泵等。其中文丘里施肥器因其结构简单、使用方便、无活动部件、无须外加动力等优点被广泛应用在农业灌溉中[4-5]。但目前国内生产的文丘里施肥器的性能和质量与国外同类产品相比尚有一定差距,例如存在水头损失大、吸肥量小等不足[6]。文丘里施肥器的结构参数对其吸肥性能有重要影响[7],改进其结构形式或结构参数能够有效地提升其综合性能。因此对文丘里施肥器进行结构优化及性能试验研究,对提升文丘里施肥器工作性能及促进新型文丘里施肥器研发有重要意义。
【研究进展】许多学者围绕文丘里施肥器结构设计、流场分析、性能测试等方面进行了大量研究,取得了较大的进展。例如,Wang 等[8]和汪小珊等[9]通过理论分析设计了SSQ 系列施肥器,并针对SSQ 系列施肥器进行了吸肥性能测试,建立了吸肥流量/效率与进出口压差的回归模型。为提高施肥精度,李欢等[10]设计了带有螺纹的文丘里施肥器,在正压施肥的条件下,该种文丘里施肥器压力损失显著降低。张建阔等[11]设计了一种双吸肥口的文丘里施肥器,在相同工作环境下吸肥量提升90%。在流场分析方面,随着计算流体动力学(Computational Fluid Dynamics, CFD)的兴起,CFD 方法被广泛用于文丘里施肥器流场分析及结构优化研究。Li 等[12]和李浩等[13]对比分析了有无空化模型的文丘里施肥器数值仿真结果,研究显示,有无空化模型在较低压差水平下,二者计算精度相当。但当空化发生之后,无空化模型的计算结果较实测值偏差较大,带有空化模型的计算结果与实测值误差较小,符合分析要求。张晓明等[14]基于湍流模型分析了扩散角、喉部直径、收缩角对吸肥性能的影响,指出喉部直径对吸肥流量影响最大。王秋良等[15]对比了收缩段与渐变段的结构形式对文丘里施肥器吸肥性能的影响,并采用Fluent 软件进行流场展示,指出喉管附近产生的真空度最大、吸力最大,增大这部分的负压有利于提升吸肥量。同时文丘里施肥器扩散段中产生了旋涡,能量耗散进一步加剧,综合吸肥性能与流场分析,王秋良等[15]认为最优的组合形式为喇叭口收缩段与流线型扩散段。在性能测试方面,王海涛等[16]针对不同工况和2 种管路布置方式进行了室内试验,指出旁路吸肥设计比旁路注肥设计工作性能更佳,可将“三通路+旁路吸肥管路”应用在实际生产中。王永涛等[5]基于三通路旁路吸肥管路进行进一步优化设计,研发了四通道并联式旁路施肥模式,研究发现四通道并联旁路吸肥模式较三通路旁路吸肥管路的吸肥流量提升31.08%。
【切入点】以上研究包含了文丘里施肥器结构优化设计、工作性能测试等方面,形成了较为完善的研究方法。但目前针对文丘里施肥器的研究主要集中在对称文丘里施肥器,其吸肥性能提升较为有限。相同工况下,非对称文丘里施肥器吸肥性能优于对称文丘里施肥器,且更加适用于低压灌溉系统。然而对于非对称文丘里施肥器的研究较少,鲜有研究对其进行结构优化,而结构参数对文丘里施肥器吸肥性能有重要影响。【拟解决的关键问题】因此,本文以非对称文丘里施肥器扩散段为研究对象,改变扩散段中心轴偏移距离,分析不同扩散段中心轴偏移距离对吸肥性能和流场分布的响应关系,以最高吸肥量及吸肥效率为目标,得到最佳结构方案,进一步提升非对称文丘里施肥器工作性能,为研发新型文丘里施肥器提供理论参考。
1 材料与方法
1.1 试验模型
非对称文丘里施肥器是基于文丘里原理进行设计的农业灌溉设备,主要由进水直管段、收缩段、喉部、扩散段、出水直管段、吸肥管等6 个部分组成。主要结构参数包括进口直径D1、出口直径D2、吸肥管直径D3、喉部直径d、收缩角α、扩散角β等(图1)。本文针对非对称文丘里施肥器进行结构优化,采用范兴科等[17]创新提出的结构数据,改变扩散段结构中心轴偏移距离Z,得到不同结构模型分别进行试验与数值仿真,其结构参数如表1 所示,F1、F2、F3、F4、F5 型施肥器对应的Z值分别是9、4.5、0、-4.5、-9 mm。其中F1 型施肥器表示范兴科等[17]提出的原型结构,其扩散段偏心向上,远离吸肥管一侧的边壁平直;F5型施肥器的扩散段是偏心向下设置,其扩散段上边壁与出口直管段上边壁水平齐平。

表1 非对称文丘里施肥器结构参数Table 1 Structural parameters of non-axisymmetric Venturi injector
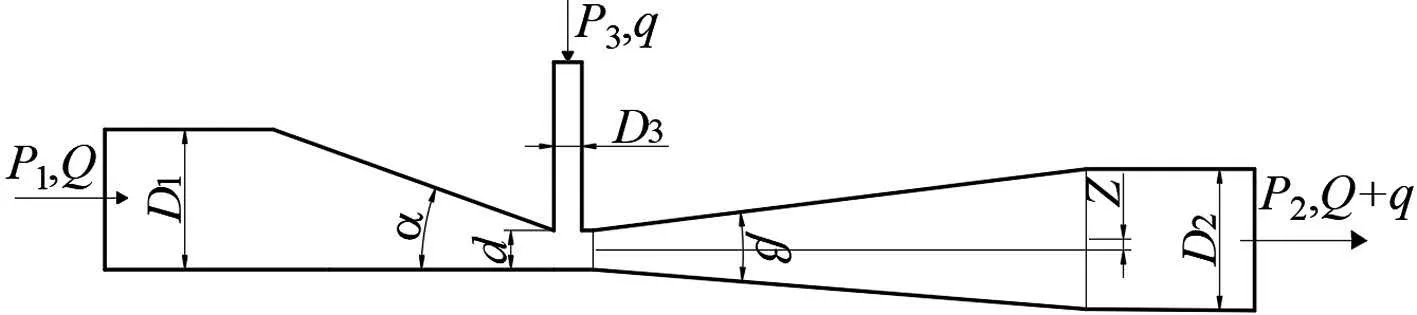
图1 非对称文丘里施肥器结构示意图Fig.1 Structure diagram of non-axisymmetric Venturi injector
1.2 试验设计
1.2.1 物理试验方案设计
本研究采用物理试验与数值仿真相结合的方法进行。根据表1 非对称文丘里施肥器结构参数,采用3D 打印技术制作实物样件,样件材料为HD-50 光敏树脂。搭建吸肥性能测试平台(图2),进行非对称文丘里施肥器性能测试。在测试过程中,通过调节控制阀1、控制阀2、控制阀3 控制非对称文丘里施肥器进出口压力,通过观测压力表1、压力表2 得到非对称文丘里施肥器进水口、出水口的压力值。为了符合现阶段大田灌溉中水压控制要求[18],设定出水口压力值P2为0.04~0.08 MPa[19],压力梯度为0.01 MPa;同时分别在每个出水口压力值的工况下,分别控制进出口压差ΔP为0.03~0.21 MPa,压差梯度为0.02 MPa;控制肥液桶液面压力为标准大气压(表2)。为使试验连续进行,采用清水代替肥液进行试验,吸肥口外接吸肥桶,每次试验时间5 min,分别测定试验前后吸肥桶中水的质量及出水口的质量,并通过计算,转换为吸肥流量q和水肥混合流量Qs。

表2 试验条件及工作参数Table 2 Test conditions and working parameters MPa
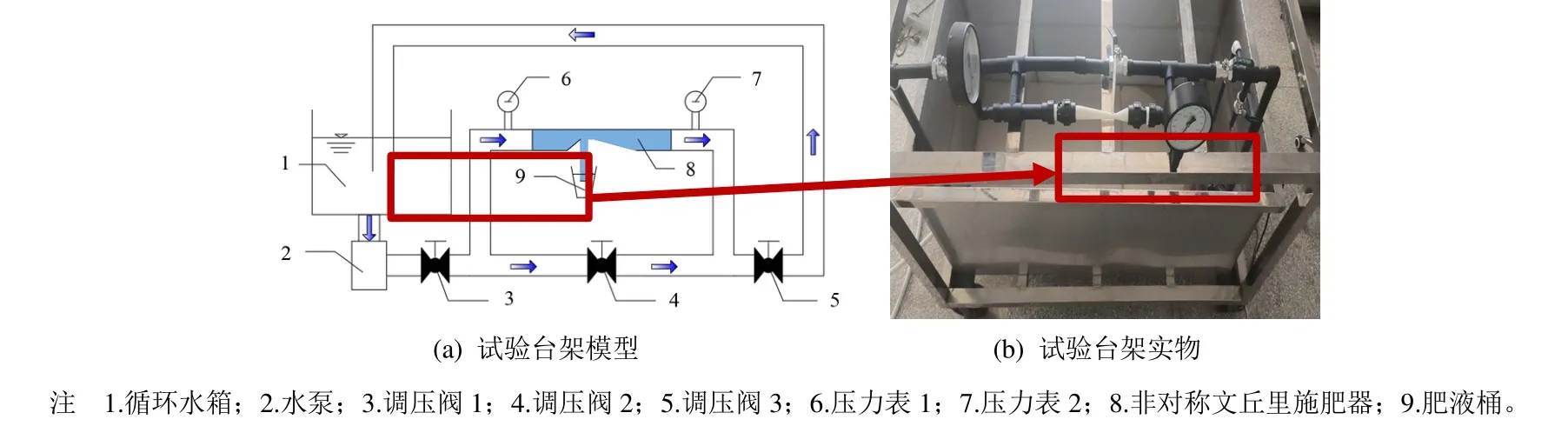
图2 试验台架结构图Fig.2 Schematic diagram of test bench structure
1.2.2 数值仿真方案设计
使用Fluent 19.0 针对非对称文丘里施肥器进行数值仿真,能有效提高试验效率、减小试验成本[20]。试验采用UG12.0 建立三维模型,采用Workbench 中Mesh 模块进行网格划分,并联动Fluent 进行网格无关性分析。根据网格无关性分析结果,选择采取最大网格尺寸为0.85 mm,膨胀率为1.05,曲率6.5°,并针对喉部、吸肥口、进水口、出水口进行局部网格加密,此时网格数量为136.4 万。
将合适的网格导入Fluent 中进行数值仿真,基于标准k-ε湍流模型进行仿真,充分考虑空化效应,激活Eulerian 多相流模型及Schnerr-Sauer 空化模型,并将Water-Liquid 设置为第1 相、Water-Vapor 设置为第2 相。采用Coupled 算法进行压力速度耦合计算,为保证计算精度,采用Second Order Upwind 算法进行仿真,并设定残差曲线收敛精度为1×10-5。边界条件设置采用表2 所设置的试验参数。为验证数值仿真结果的可靠性,将模拟值与试验值进行对比分析(图3),结果显示,试验值与模拟值相对误差仅为2.39%~5.21%,相对误差小于10%,说明计算结果较为可靠[21]。
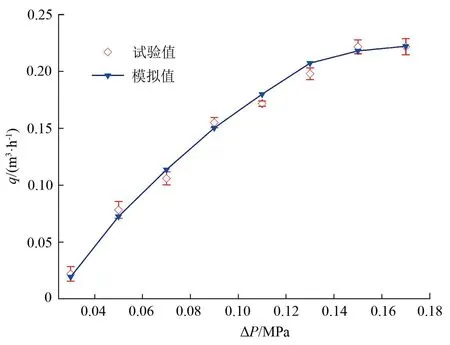
图3 数值仿真与物理试验对比Fig.3 Comparison of numerical simulation value and physical test value
1.3 数据处理
1.3.1 吸肥性能指标计算
非对称文丘里施肥器主要性能指标包括吸肥流量q,吸肥效率η,其中吸肥流量q可采用吸肥性能试验直接测得,吸肥效率η计算式为:
式中:Q为进水口流量(m3/h);P1为进水口压力值(MPa);P2为出水口压力值(MPa);P3为进肥口压力值(MPa)。
除以上吸肥性能指标外,最大吸肥流量也是衡量非对称文丘里施肥器性能的重要指标。
1.3.2 水力性能指标计算
进水口临界吸肥压力、临界吸肥压差是衡量非对称文丘里施肥器水头损失的重要指标。本文中采用物理试验的方式测定了进水口临界吸肥压力,临界吸肥压差计算式为:
式中:ΔPs为临界吸肥压差(MPa);P1,S为进水口临界吸肥压力值,即在固定出水口压力值下,吸肥口刚开始吸肥时的进水口压力值(MPa);P2,S为刚吸肥时出水口压力值,其值与P1,S相对应(MPa)。
2 结果与分析
2.1 扩散段中心轴偏移距离对吸肥性能的影响
固定其他结构参数,将扩散段及出水直管段向下移动,文丘里施肥器最大吸肥流量逐渐提升。随着向下移动的距离越大,最大吸肥流量提升越明显。与F1 施肥器相比,相同工况下,F5 施肥器的吸肥流量提升13.03%(图4(a))。这说明将非对称文丘里施肥器扩散段及出口直管段向下偏心设计更有利于提升文丘里施肥器的最大吸肥流量。
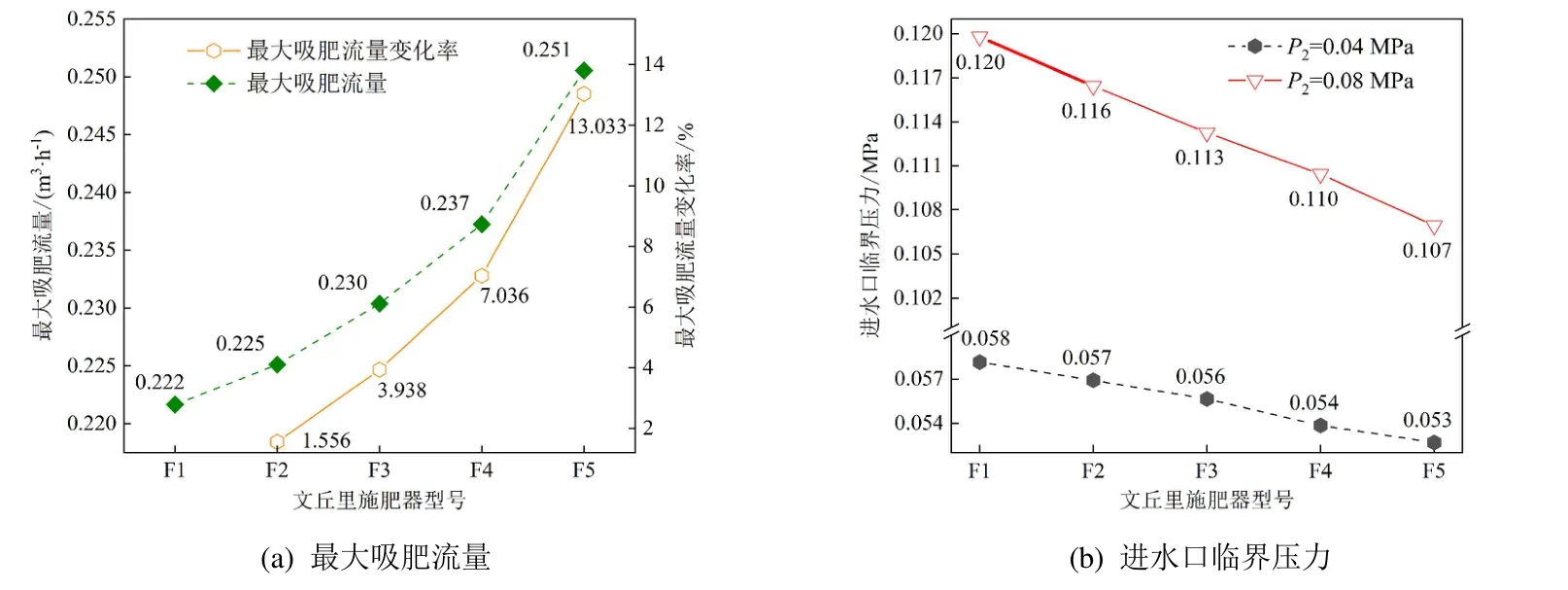
图4 不同模型工作范围对比Fig.4 Comparison of working range of different models
临界吸肥压差是衡量文丘里施肥器工作性能的重要指标之一,能够表征文丘里施肥器工作时水头损失[22]。当固定出水口压力时,吸肥临界压差也可采用进水口临界压力表示。出水口压力升高时,进水口临界压力明显上升(图4(b))。将扩散段和出水直管段向下移动有利于减小进水口临界压力,即有利于减小吸肥临界压差。与F1 施肥器相比,F5 施肥器的进水口吸肥临界压力分别降低7.69%(P2=0.04 MPa)和7.60%(P2=0.08 MPa)。这说明将非对称文丘里施肥器扩散段及出口直管段向下偏心设计更有利于提升文丘里施肥器工作范围。
2.2 进出口压差对吸肥性能的影响
随着进出口压差的增大,吸肥流量逐渐增大,且增大的趋势逐渐减小。与ΔP=0.15 MPa 时的吸肥量相比,ΔP=0.17 MPa 时,其吸肥量变化率为0.05%左右,此时认为文丘里施肥器达到极限工况。这是因为随着进出口压差的增大,喉部负压逐渐增大,当达到空化临界压差时,喉部负压将不再随着进出口压差的增大而增大。在相同工况下,将非对称文丘里施肥器扩散段及出水直管段向下移动,吸肥流量逐渐提升,与F1 施肥器相比,F5 施肥器的吸肥流量增大13.03%~40.16%,随着进出口压差的增大,增大的幅度逐渐减小(图5(a))。
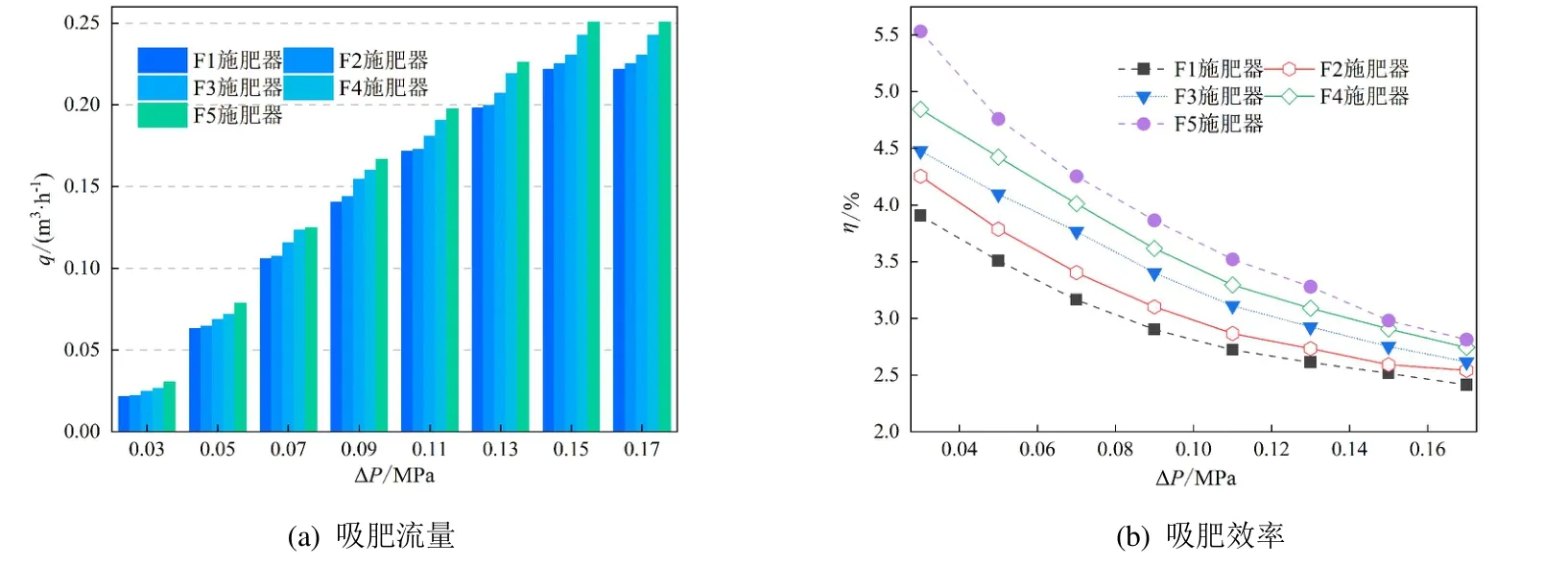
图5 不同压差下文丘里施肥器的吸肥流量及吸肥效率(P2=0.04 MPa)Fig.5 The Venturi injectors’flow and efficiency of fertilizer absorption under different pressure difference (P2=0.04 MPa)
随着进出口压差的增大,文丘里施肥器的吸肥效率逐渐下降,下降的速率逐渐降低,当进出口压差为0.17 MPa 时,F1—F5 施肥器的吸肥效率相近。与F1施肥器相比,相同工况下,F2—F5 施肥器的吸肥效率均有不同程度的上升,表现为F5 施肥器>F4 施肥器>F3 施肥器>F2 施肥器>F1 施肥器,随着进出口压差的增大,吸肥效率提升幅度逐渐减小,F5 施肥器比F1施肥器的吸肥效率增加12.09%~39.13%(图2(b))。
2.3 水力性能对比分析
2.3.1 出水口压力对吸肥性能的影响
在文丘里施肥器达到最大吸肥流量之前,吸肥流量与进水口压力呈较好的线性关系,吸肥流量与进水口压力值正相关,相同模型下,最大吸肥量相近(图6)。图6 中关系曲线与横坐标轴的交点为吸肥流量为0 时的进水口压力值,这被认为是某一出口压力下,正常吸肥所需要的最低进水口压力,即为进水口临界吸肥压力,随着出水口压力值的增大,进水口临界吸肥压力值升高,能量损失更大。P1-q拟合曲线的斜率表示进水口压力变化时吸肥流量的变化情况。斜率越大,说明吸肥流量对进水口压力的敏感程度更高,即在相同进水口压力下的能量转换效率越高。随着出水口压力值的增大,P1-q拟合曲线的斜率逐渐降低,这说明其能量转换效率更低。
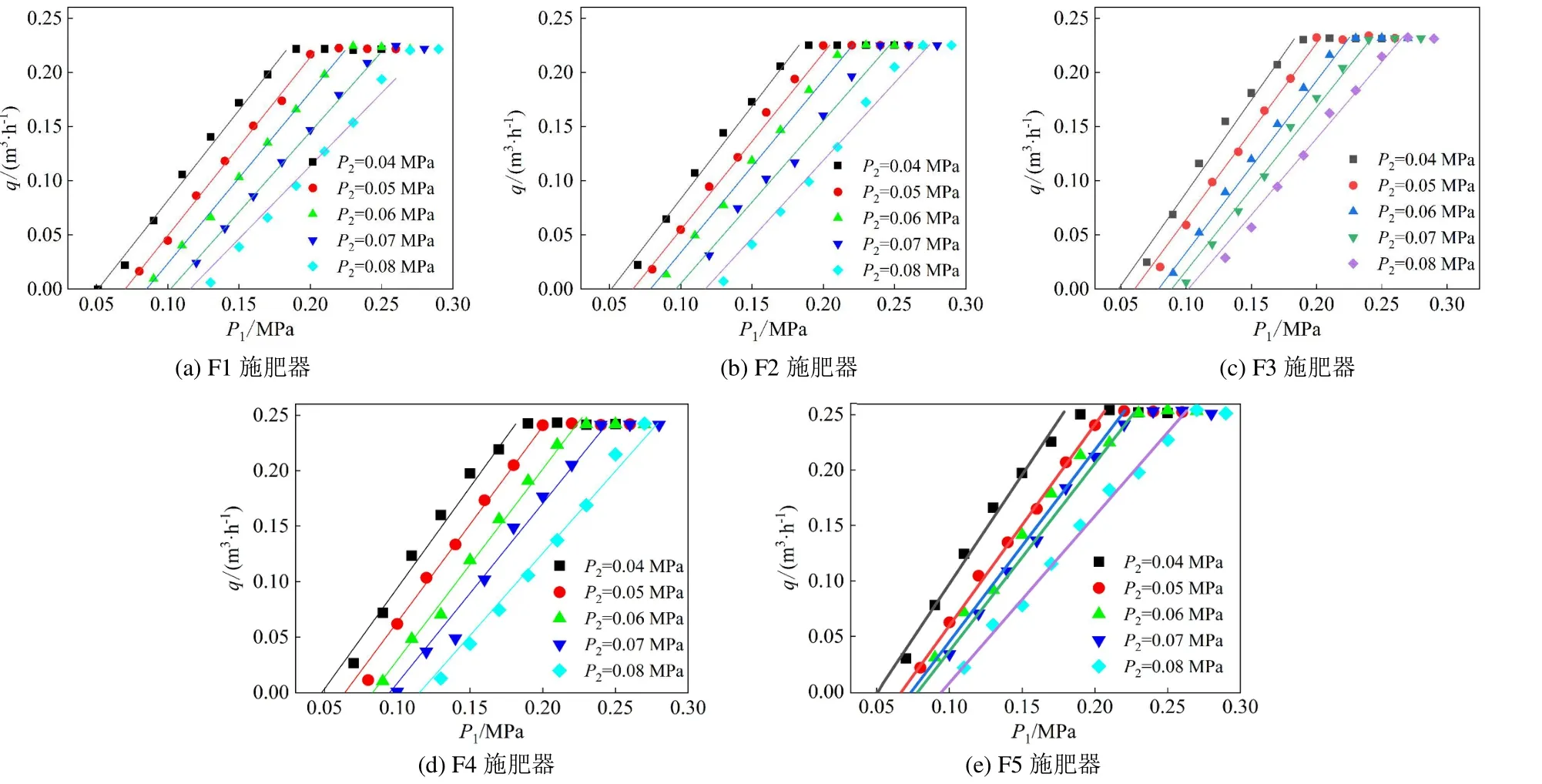
图6 进水口压力与吸肥流量关系曲线Fig.6 Relationship curve between inlet pressure and fertilizer flow rate
表3对比了F1施肥器与F5施肥器在各工况下P1-q的拟合曲线及相关参数。与F1 施肥器相比,在相同工况下,F5 施肥器的斜率提高9.17%~17.74%,说明将扩散段向下移动有利于提高文丘里施肥器能量转换效率。F5 施肥器的P1-q拟合曲线与X 轴交点数值比F1施肥器下降16.67%左右,表明F5 型施肥器入水口临界吸肥压力更低,水头损失更小,更有利于低压灌溉。
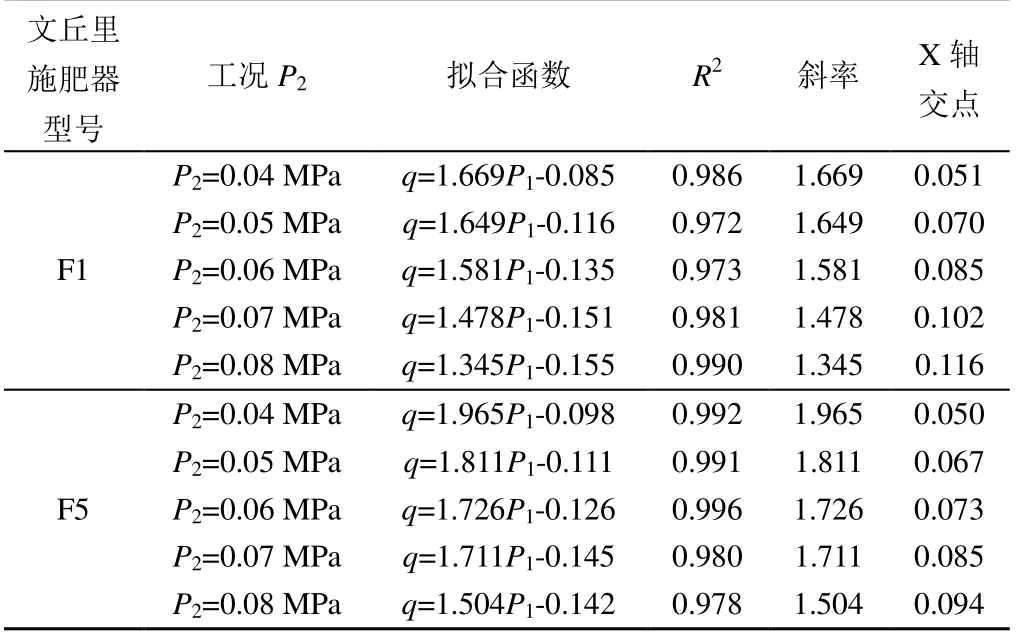
表3 F1、F5 施肥器的P1-q 拟合曲线参数Table 3 Parameter table of F1 and F5 P1-q fitting curve
2.3.2 湍流动能
图7 为不同文丘里施肥器湍流动能大小(k)。湍流动能是表示流体运动的紊流状态,是衡量文丘里施肥器水力性能的重要指标之一。湍流动能越大,说明文丘里施肥器内部流态越紊乱,其水肥混合能力越强,但同时水头损失越大。湍流动能在喉部进口处开始增加,在扩散段前端达到最大(图7)。这是因为水流流经喉部时,流速增大,压强减小,吸肥管中的肥液在大气压的作用下进入喉部,与喉部中水流进行掺混。扩散段前端湍流动能分布区域最大,这说明扩散段中水肥掺混强度最高,多方向速度碰撞剧烈,流态紊乱。在相同工作条件下,湍流动能及其分布区域表现为F5施肥器 图7 P1=0.15 MPa、P2=0.04 MPa 时文丘里施肥器湍流动能分布Fig.7 Turbulent kinetic energy distribution nephogram of Venturi injector at P1=0.15 MPa and P2=0.04 MPa 本文对比分析了不同的扩散段中心轴偏移距离对非对称文丘里施肥器吸肥性能、水力性能的影响。试验表明,在某个阶段文丘里施肥器开始吸肥,此时增加进出口压差,吸肥量逐渐增加。在此阶段之内,压差与进口压力呈现良好的线性关系。当达到最大吸肥量时,吸肥量不再随着进出口压差的增大而增大,这与Wang 等[8]的研究结果一致。因此,若文丘里施肥器在最大吸肥量的工况下运行,可选择较小的进口压力,如果在较大的进水口压力下运行,将导致能量的额外损失,同时增大了空化发生的风险,进一步抑制了吸肥性能的持续提升。在相同的进出口压差下,出水口压力值越高,临界吸肥压差越大。这是因为当出水口压力值升高时,进水口压力需要克服出口回水阻力的所需能量越多,能量转换效率越低。因此在实际运行过程中,应该尽可能地降低出水口压力,保证非对称文丘里施肥器高效稳定运行。 本研究中,发现将扩散段中心轴偏移距离向远离吸肥管的一侧移动,有利于降低文丘里施肥器水头损失,提升文丘里施肥器吸肥性能。其原因是将扩散段远离喉部吸肥管一侧设置时,在水流流经喉部进入扩散段后,主流区斜切向下,此时吸肥管中的肥液与主水流呈钝角,减小了吸肥管中肥液与喉部中水流的碰撞概率,使得多方向速度碰撞程度减小,从而使得文丘里施肥器能量损失减小。而F1 施肥器主流靠近远离吸肥管的一侧,虽然下部流线平稳,但其吸肥管中肥液与喉部中水流流向呈锐角或者直角,肥液进入喉部克服的阻力更大。同时,在水肥掺混的过程中,流层之间能量交换迅速,将会产生较大的水头损失[23]。当扩散段中水流产生偏斜流动时,水肥掺混的部位离喉部较远,此时降低了水肥掺混时流态对喉部负压形成的影响。Manzano 等[24]指出,提高喉部负压的利用效率,有利于提升文丘里施肥器吸肥量。这也验证了F5 施肥器最大吸肥流量大于F1 施肥器。因此,在设计文丘里施肥器结构时,可考虑改善喉部附近流态,减小其他因素对喉部负压的影响,以此提高文丘里施肥器综合性能。 本文中只研究了扩散段中心轴偏移距离对吸肥性能的影响,并未对扩散段其他结构参数进行进一步研究,在后续的研究过程中,仍需对喉部直径、渐变段角度等各参数进行进一步优化研究,进一步提升非对称文丘里施肥器工作性能。 1)非对称文丘里施肥器在正常工作阶段,吸肥量与进口压力呈良好的线性关系,当进出口压差在0.15 MPa 左右,吸肥流量达到最大值,此时达到非对称文丘里施肥器极限工况。 2)达到极限工况时,相同模型下,最大吸肥流量不随进出口压差和出水口压力的变化而变化,而是一个相对稳定的值。临界吸肥压差和进水口临界吸肥压力均随着出水口压力的增大而增大。 3)与F1 施肥器相比,F5 施肥器的吸肥流量和吸肥效率分别提升13.03%~40.16%和12.09%~39.13%,且增幅随着进口压力值的增大逐渐降低,其最大吸肥流量提升13.03%,临界压差降低7.69%。将扩散段向着远离吸肥管一侧移动,有利于降低局部水头损失,提高喉部负压利用效率,提升极限工况下吸肥流量,降低吸肥临界压差,提升文丘里施肥器整体工作性能。 (作者声明本文无实际或潜在的利益冲突)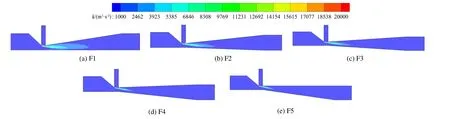
3 讨 论
4 结 论
