淹没柔性植被河道阻力系数特性及计算方法研究
2023-07-04赵汗青王伟杰赵彦芳冯达骞李今今徐宇轩
赵汗青,王伟杰,赵彦芳,4,冯达骞,4,李今今,徐宇轩,5
(1. 中国长江三峡集团有限公司,科学技术研究院,北京 100038; 2. 水资源高效利用与工程安全国家工程研究中心,江苏 南京 210024; 3. 中国水利水电科学研究院,流域水循环模拟与调控国家重点实验室,北京 100038;4. 河北工程大学水利学院,河北 邯郸 056000; 5. 华北水利水电大学水利学院,河南 郑州 450045)
0 引 言
植被是河道生态系统中不可或缺的组成部分,它具有许多生态功能。例如通过根系固定来保持河床稳定性,通过表皮的吸收能力来改善水质,并通过为生物提供附着基质和栖息地来丰富生物多样性特征,因此植被被广泛应用于河道生态系统的修复和重建。但植被的存在会阻碍水流运动,降低水流流速,抬升河道水位,影响河道的行洪能力。柔性植被的阻水机理更为复杂,在水流影响下表现出一定的运动和弯曲,从而导致植被顶部的水流更加紊乱,影响了河道局部水流的变化。因此,开展柔性植被的阻力特性研究对改善河道生态环境,计算河道防洪能力具有重要意义[1]。已有研究更多侧重物理过程描述和基于基理的分析,如Wang[2]利用水槽实验推断出局部均匀流中孤立圆柱体的阻力系数(Cd)呈现出接近抛物线的形状,在最密集的树冠情况下达到峰值,并将这种Cd(x)变化的结果总结为体积阻力公式;Okamoto 和Nezu[3]使用粒子图像测速仪(PIV)在有淹没植被明渠水流中进行湍流测量;Yang 和Choi[4]提出了一种速度关系,用于预测植被中两层流的速度分布;Wang[5]建立了描述沉水植物归一化阻力与基于植物有效高度的雷诺数之间关系的方程,并用于计算不同生长阶段沉水植物的植被阻力参数。但是大部分研究者没有考虑植被本身形态的影响,尚未形成含植被形态变化的阻力系数计算公式,因此,将柔性植被的变形加入其中,提出了淹没柔性植被河道阻力系数的计算方法。该方法可应用于不同水深、不同植被密度、不同植被高度等条件下的淹没柔性植被河道阻力系数计算,其结果可对河流生态保护及防洪措施提供理论依据。
1 研究方法
1.1 理论分析
经典Darcy-Weisbach 公式由Darcy 和Weisbach 提出,现在被广泛应用于明渠中摩擦损失的计算[6]。其中的达西-魏斯巴赫阻力系数f可表示为:

在有植被存在的情况下,水流与边界产生的湍流剪应力远小于由植被形状所产生的剪应力,因此可忽略不计,故有:

式中:Cd为植被阻力系数;m为植被密度;D为植被杆径;hv为植被高度;Uv为植被层水流运动速度。
联立公式(1)、(2)可得:

其中:Lc=(CdmD)-1为调整长度尺度;
对于淹没植被的情况,计算植被阻力系数的核心是确定植被层中的水流速度与整体断面平均流速的比值。定义Us为淹没植被上方的自由水层的断面平均流速,定义ΔU=Us-Uv为自由水层流速与植被层流速的差。则有:

式中:hw为水深。
结合式(4)及ΔU的定义,有:

将式(5)代入式(3),得:

考虑到淹没柔性植被会在水流作用下发生弯曲,故将柔性植被弯曲前的高度引入公式(6)。

式中:hc为柔性植被弯曲前的高度。
由式(7)可以看出,hc/Lc、hv/hc及hc/hw反映了植被阻力系数、植被分布密度、植被杆径、植被高度、水深、弯曲前后形态变化的综合作用;而且ΔU/Uv也随着hc/Lc、hv/hc及hc/hw变化而变化。
由此,可得到三个无量纲因子hc/Lc、hv/hc及hc/hw。
定义:

Wang[7]等 根 据 一 维 闭 合 数 值 模 型 建 立ΔU和Uv的 相 关关系:

式中:c1、c2、c3均为参数。
由式(7)、(8)、(9)可建立f与α、β、γ之间的函数关系,其中,α、β、γ为自变量,f为因变量,得到f的一般公式为:

由式(10)可得f与α、β、γ三个参数相关关系为:

1.2 最大差异性算法
利用最大差异性算法(MDA)将原始数据进行选择分类。MDA 的目标是从大小为N的数据库中选择大小为M的代表性子集。将N维向量组成的数据样本X={x1,x2,…,xn},通过该算法得到代表数据多样性的向量子集{v1,…,vm},通过从数据样本{v1}传输一个向量来初始化子集,迭代选择剩余的M-1 个元素,计算数据库中每个剩余数据与子集元素之间的不相似性,并将最不相似的元素转移到子集。当算法达到M次迭代时,该过程结束[8]。在该方法中,子集的初始数据作为数据样本中相对于其他数据样本的差异和最大的向量。在选择数据的过程中,计算数据库中每个剩余向量与子集中每个向量的相异度,并建立数据库中每个向量与子集中每个向量的唯一相异度来定义最相异的一个。本文即从实验数据中选择出训练组、测试组组和验证组。
1.3 遗传算法
遗传算法是将达尔文遗传规律和自然淘汰的生物进化过程作为理论依据,将原始数据作为初代种群,通过对交叉和变异过程的模拟,筛选并储存适应度较好的个体,并对筛选过程重复进行,最终得到个体的最优解。遗传算法的主要步骤为生成原始种群、选择、交叉和变异[7]。利用集成遗传算法的程序Eureqa来寻找公式,具体步骤为[9]:①输入数据。将由最大差异性算法分类得到的训练组和测试组数据依次输入到程序中。②初始化。程序内部的符号函数生成器会随机的将算子和算符结合起来。本文用到的算符有加、减、乘、除和幂。初始解不用于进化,当子表达式的变化不会导致解的精度超出程序给定的范围时,该子表达式将会被废除。③交叉及变异。运用选定的精度标准对表达式的预测值和验证组的实测值进行比较,舍弃掉不符合标准的表达式,剩下的表达式利用程序内置的概率函数进行杂交,并生成新的表达式。④程序会生成一系列不同精度和复杂度的表达式,需要根据表达式表现的物理意义、精度和复杂度来选择合适的表达式,随即终止程序运行。
在寻找目标表达式的过程中需要遵循两个原则:①为防止公式的过度拟合,需及时终止程序;②选择表达式同时兼顾解的误差和公式的复杂度[10]。
2 数据分析与公式构建
2.1 实验数据整理与分析
利用文献检索,收集到不同条件下的试验数据。试验数据的相关信息如表1 所示。对收集到的数据进行筛选处理,最终得到89组实验数据。使用最大差异性算法对数据进行选择,将训练组、测试组和验证组的数据按照4∶4∶2的比例进行分配。3组实验数据统计见表2。将训练组和验证组数据导入到Eureqa软件中,进行公式拟合。利用Matlab 程序将实验数据进行分类,分类结果如图1所示。

图1 不同数据组分布图Fig.1 Distribution of different data groups

表1 实验数据的相关信息列表Tab.1 List of relevant information of experimental data

表2 实验数据统计Tab.2 Experimental data statistics
2.2 柔性植被阻力系数公式构建
根据最大差异性算法选择的数据,再利用Eureqa 程序寻找计算公式。Eureqa 程序可以寻找原始数据里变量的关联性,然后提出来一系列公式来描述出来。在公式搜索过程中,利用适应度函数评估每个候选解,并且还考虑了求解公式的复杂度。当公式中变量的个数、系数和公式中包含的运算符号和类型增加时,公式的复杂度也会随之增加。软件会在复杂度相同的情况下保存误差较小的预测公式。本此公式的搜寻,有14组公式被保留,其中复杂度最小为1,最大为40。求解结果如表3所示。

表3 公式求解Tab.3 Formula solution
图2 描述了Pareto 前沿,总体看来,误差与复杂度之间大致呈负相关关系,当公式复杂度增加时,误差会随之变小。当公式较为简单时,会导致计算值与实测值过度拟合,公式的物理意义不大;但当复杂度提升到一定程度时,模拟的精度提高的并不明显。
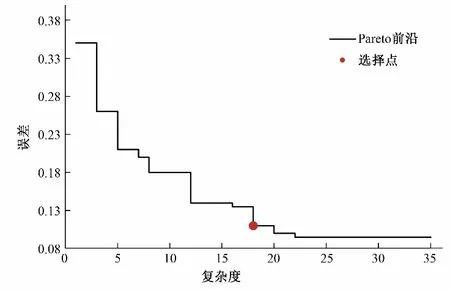
图2 Pareto前沿Fig.2 Pareto frontier
当公式的复杂度分别为16、18、20 时,复杂度由16 变到18时误差的变化较大,但当复杂度由18 变为20 时误差变化不明显,且公式复杂度为18时,复杂度适中,拟合程度良好。综上所述,选择复杂度为18的公式作为最终公式,即:

式(12)公式拟合程度较好,表达形式相对简单,可以准确、清晰的表达出淹没柔性植被形态特征与阻力系数之间的关系。
在实际工程应用中,曼宁系数的使用相对较多,其与Dacy-Weisbach系数f存在定量关系:

式中:R为水力半径;g为重力加速度,取9.8 m/s2。
联立式(12)、(13)得到曼宁系数n与各个无量纲因子之间的定量关系。

2.3 公式计算值与实测值的对比分析
为了评价本文公式的拟合程度,将测试组的数据代入本文公式中来对阻力系数进行计算。采用相关系数(r)及均方根误差(RMSE)评价f、n与各个无量纲因子之间的拟合程度。
相关系数(r)表示如下:

式中:Xi、Yi为两个不同的变量(在本发明中分别表示为计算值和实测值)分别为变量Xi、Yi的均值;N为数据长度。
r值的绝对值介于0~1 之间。通常来说,r越接近1,表示X、Y两个量之间的相关程度就越强,反之,r越接近于0,X、Y两个变量之间的相关程度就越弱。
均方根误差(RMSE)是用于表征计算值与实测值曲线的拟合程度,均方根误差越小,拟合程度越高。公式表示为:
式中:Xi、Yi分别为计算值和实测值;N为数据长度。
将河道阻力系数f和曼宁系数n的公式计算值与试验测量值进行统计分析,结果见图3。

图3 f、n实测值与计算值对比Fig3 Comparison of measured and calculated values of f and n
由图3 可看出,达西-魏斯巴赫阻力系数f的公式计算值和实验测量值的相关系数为0.96,均方根误差为0.07;曼宁系数n的公式计算值和实验测量值的相关系数为0.95,均方根误差为0.005 9。由此可看出本文提出的淹没柔性植被河道阻力系数f与曼宁系数n计算值与实测值拟合较好,即该公式可以很好的用来计算淹没柔性植被的河道阻力系数。
3 结 论
本文将柔性植被的变形考虑其中,首先分析了达西-魏斯巴赫阻力系数与淹没度及植被属性之间的相关关系,然后将数据进行筛选处理,利用最大差异性算法将实验数据进行选择分类,运用遗传算法寻找因变量和自变量之间的关系,再通过对表达式复杂度、误差的分析,以及不同阻力系数之间的转换关系,提出并验证了淹没柔性植被河道的达西-魏斯巴赫阻力系数公式及曼宁系数公式,为植被化生态河道设计提供理论基础。
