三角代数上σ－三重可导映射的可加性*

罗湘亿，霍东华

（1.东北林业大学；2.牡丹江师范学院）

0 引言与预备知识

算子代数的相关理论在20世纪的30年代所产生，它的研究领域在泛函分析中占有极大地位.算子代数与数学的其他分支紧密联系并相互渗透，并且算子代数理论在交换几何，数论，量子力学，控制理论，线性系统之类的学科中应用非常广泛.算子代数主要的研究方向是讨论代数的结构并且用同态映射来研究代数分类.由于算子代数的一些固有性质和算子代数上的某些映射有紧密联系，所以众多学者先研究算子代数上的映射，从而进一步研究算子代数的结构.

三角代数是很重要的一类非自伴非素的算子代数，同样非自伴非素的算子代数还有套代数和上三角矩阵代数.近几年来，三角代数上的可导映射以及导子的研究已取得许多成果.Cheung主要研究了三角代数上的Lie 导子、同构映射以及交换映射，其中包含了很多如非平凡套代数里的标准子代数，上三角矩阵代数这类的非自伴算子代数［1］.Wang主要研究三角代数上的k－交换

映射［2］.Dominik 主要对三角代数上的广义Lie导子与三角代数上的双导子进行研究［3］.纪培胜主要研究非线性Lie 导子和三角代数上的广义Lie导子的结构［4］.Lu 证明得出在自反代数上Lie导子也能够分解成中心值迹与导子的和［5］.观察上述这些丰富的成果，可以发现这类可导映射都研究了可加性这个性质.最开始是由Daif M详细叙述了在素环上满足δ (ab ) ＝δ (a ) b ＋aδ (b )的映射δ 具有自动可加性［6］，这个结论让许多学者惊奇，在此之后，与这类结论相类似的很少，但是这类有意义的研究问题还有很多.

该文是在三角代数σ－可导映射的基础上更深层次地进行研究，将范围扩展到3个变元的情形，讨论在三角代数上σ－三重可导映射的可加性，并证明了Δ是一个σ－三重可导映射.

定义1［7］设A是一个代数，M是A－双模.δ：A →M为可加映射.如果对任意的x，y ∈A，有δ (xy ) ＝δ (x ) y ＋xδ (y )成立，称δ为从A到M的导子.

定义2［7］设ℑ是代数或环，δ 为ℑ上的可加映射，σ是ℑ上的一个自同构，idℑ是ℑ上的恒等映射.若对任意的x，y ∈ℑ，有δ (xy ) ＝δ (x ) y＋σ (x ) δ (y )，则称δ是σ－导子.当σ ＝idℑ时，Jordan σ－导子就为Jordan 导子，σ－导子就为导子.

定义3［8］设A与B为交换环R上含有单位元的代数，如果M 不仅是A 的左模还是B 的右模，则称M为(A，B)－双边模，若a ∈A，b ∈B且对任意的m ∈M，有am ＝mb ＝0蕴含a ＝b ＝0，则称M是(A，B)－忠实双边模.在M是(A，B)－忠实双边模的前提下

在通常矩阵的乘法和加法运算下为一个三角代数.

定义4［8］设IA是代数A的单位元，设IB是B的单位元，I是三角代数U中的单位元.记e1与e2分别为

用Z (U )表示U中心.

定义6［10］下方将三角代数U再做一次分解，对任意的x ∈U，由于

则三角代数U可以分解成

1 主要结论与证明

1.1 σa 和Δ的可导性

设U是一个三角代数，δ 是U上的一个映射（无可加性假设），σ 是U上的一个自同构.如果任意的x，y，z ∈ U，有δ (xyz ) ＝ δ (x ) yz ＋σ (x ) δ (y ) z ＋σ (x ) σ (y ) δ (z )，则δ 是一个可加的σ－三重导子.

定理中包含了一些主要符号，如C表示复数域，R 表示实数域，H 表示Hilbert 空间，U ＝Tri (A，M，B)表示三角代数，AlgN 表示与套N 相关的套代数，B (H )表示H 上的全体有界线性算子，Mn×n(R )表示R 上的n × n 矩阵代数，Tn(R )表示R上的n × n上三角矩阵代数，等等.

设U是一个三角代数，δ 是U上的一个映射（无可加性假设），σ 是U上的一个自同构.设a ＝f1δ (e1) e2－f2δ (e1) e1，对任意的x ∈U，定义映射σa(x ) ＝σ (x ) a－ax，则下面证明σa是一个σ－三重可导映射.

定理1令σa(x ) ＝σ (x ) a－ax，则∀x，y，z ∈U，有

证明∀x，y，z ∈U，由于

而

所以

证毕.

对任意的x ∈U，再定义映射Δ (x ) ＝δ (x )－σa(x )，则下证Δ是一个σ－三重可导映射.

定理2令Δ (x ) ＝δ (x )－σa(x )，如果任意的x，y，z ∈U有

则有

证明由于

因此Δ (xyz ) ＝Δ (x ) yz ＋ σ (x ) Δy·z ＋σ (x ) σ (y ) Δz.则Δ是一个σ－三重可导映射.

1.2 三角代数上σ－三重可导映射的可加性

引理1Δ (0 ) ＝0，Δ (e1) ＝Δ (e2) ＝0

证明由于σ是同构，从而σ (0 ) ＝0，进而

下证Δ (e1) ＝0由于e1e1e1＝e1，从而

在式（1）两端右乘e1，可得

因此

在式（1）两端左乘f2、右乘e2可得

因此

由式（2）、（3），可得

由σa的定义有

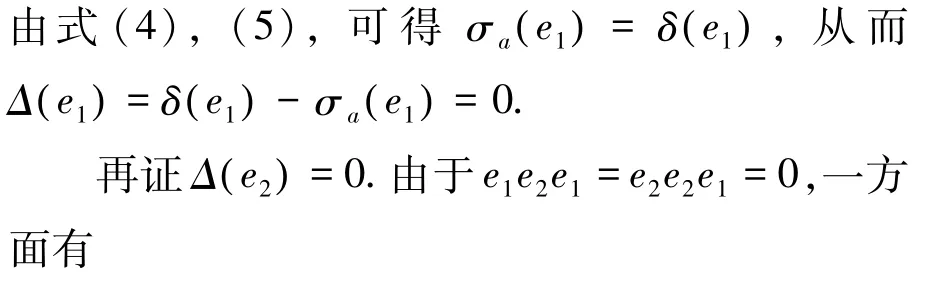
即

另一方面有

即

又由于

所以

由式（8）得

从而

②对任意的x，y，z ∈U，一方面有

另一方面由引理3中③，有

比较式（20）和（21）得

由于σ 是三角代数U 上的一个同构，从而由式（22），得

定理3设U是一个三角代数，δ 是U上的一个映射（无可加性假设），σ是U上的一个自同构.如果任意的x，y，z ∈U，有δ (xyz ) ＝δ (x ) yz ＋σ (x ) δ (y ) z ＋σ (x ) σ (y ) δ (z )，则δ 是一个可加的σ－三重导子.

证明对任意的x，y ∈U，由引理2，引理4有

即Δ是三角代数U上一个可加的σ－三重导子.又由于σa在U上也是可加的σ－三重导子，从而δ ( x) ＝Δ ( x) ＋σa( x) ( ∀x ∈U)是一个可加的σ－三重导子.

由于上三角分块矩阵代数和套代数是两类特殊的三角代数，从而可将定理1的结论用到这两类代数上，可得以下两个推论.

推论2设N是数域F上无限维Hilbert空间H上的一个非平凡套，δ是套代数AlgN上的一个映射（无可加性假设），σ 是AlgN 上的一个自同构.如果对任意的算子A，B，C ∈AlgN，都有δ (ABC) ＝ δ (A ) BC ＋ σ (A ) δ (B ) C ＋σ (A ) σ (B ) δ (C )，则δ是一个可加的σ－三重导子.

2 总结

三角代数上关于可导映射的研究是三角代数中的一个重要的方向，对于众多学者更深层次的理解与认识三角代数的结构来说至关重要.所以该文使用了代数分解方法以及代数的结构的性质主要研究了三角代数上σ－三重可导映射是否具有自动可加性.

该文是在三角代数σ－可导映射［7］的基础上更深层次地进行研究，将范围扩展到3个变元的情形，讨论在三角代数上σ－三重可导映射的可加性，首先对即将用到的定义进行叙述，其次定义了映射σa，证明了σa是一个σ－三重可导映射.再次定义了一个映射Δ (x ) ＝δ (x )－σa(x )，证明了Δ是一个σ－三重可导映射.随后给出了主要定理，如果等式δ (xyz ) ＝δ (x ) yz ＋σ (x ) δ (y ) z ＋σ (x ) σ (y ) z ＋σ (x ) σ (y ) δ (z )成立，则δ 是一个可加的σ－三重导子.