积分微分方程组非局部边值问题的再生核数值方法

刘 畅，周永芳

（河北工业大学）

0 引言

在许多学科中经常涉及到积分微分方程组问题，并且在许多领域也有广泛的应用，如控制理论、天文学、生物物理学、电动力学、电磁理论、空气动力学、经济学、生态学、医学和生物学.积分微分方程组通常难以获得解析解，所以必须借助数值方法来获得有效的近似解.多年来，人们对积分微分方程问题的数值解进行了大量的研究工作，采用了许多不同的方法.用于求解这些问题的数值方法包括同伦分析法［1］、同伦摄动方法［2］、He 同伦摄动法［3］、修正的新迭代方法［4］、泰勒配置方法［5］、伯恩斯坦配置方法［6］、勒让德多小波方法［7］、变分迭代方法［8］、伪谱方法［9］、谱方法［10］、移位雅可比－高斯配置法［11］和Adomian分解法［12］.

该文考虑以下积分微分方程组问题：

该文主要介绍一种在再生核空间中求解具有非局部边界条件的积分微分方程组的数值方法.再生核理论在数值分析、微分方程、概率统计等方面有着重要的应用.再生核数值方法在求解常微分方程问题［13］，积分方程问题［14］，偏微分方程问题［15］都有广泛的应用.Zhang 提出了一种求解带Kalman核的弱奇异Fredholm积分微分方程的广义配置方法［16］.周永芳利用再生核数值方法解决了非局部边值的偏微分方程问题［17］.Ghasemi在处理非局部的积分微分方程组问题时得到了具有易于计算分量的收敛级数形式的解［18］.

再生核数值方法在方程求解的问题上已经相对成熟，但对于方程组问题的研究还不够深入，尤其是带有非局部边值条件的方程组.通常满足非局部边值条件的再生核空间难以构造，使得求解过程中的计算量增大，精度降低.针对这一难点，该文直接构造一般形式的再生核空间，在这样的再生核空间中去求得满足边值条件的近似解，与传统再生核数值方法相比，计算更为方便快捷.数值结果表明该方法具有较高的精度.

1 预备知识

1.1 勒让德多尺度小波基的构造

首先，介绍在L2［0，1］上的三次勒让德函数：

将三次勒让德函数作为尺度函数构建L2［0，1］上的三次勒让德小波：

由此可以得到多小波

其中p ＝0，1，2，3，r ＝0，1，…，2h－1－1，h ＝1，2，3，…｝.

为了方便，将多小波记作：

1.2 再生核空间的构造

W2m＋1［0，1］的内积为：

范数：

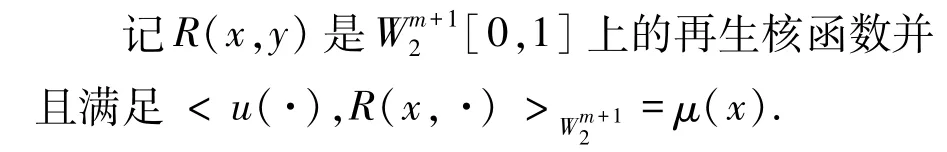
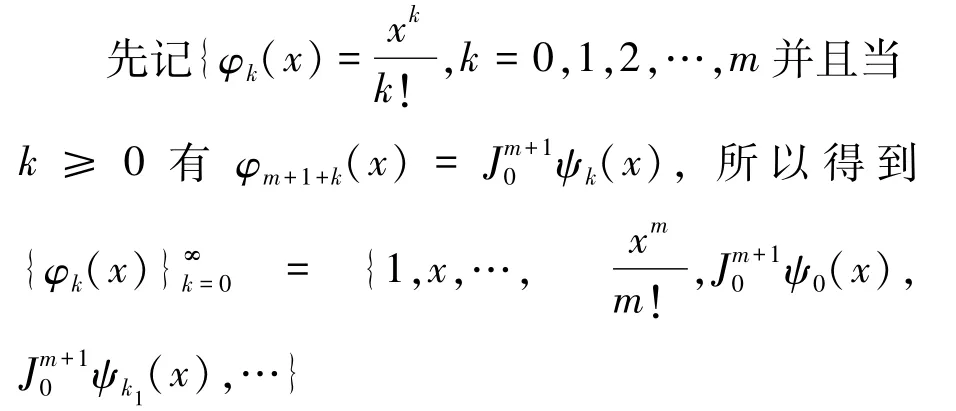
2 配置法

当s ＝l时，有

当s ≠l时，有

其中l，s ＝1，2，…，n.

定理2.1是有界线性算子，其中l，s ＝1，2，…，n.

证明首先考虑当l ≠s时，有

下面考虑它的范数

接下来考虑求解算子方程组，只要求得算子方程组的解就能得到问题（1）的解.下面给出ε－近似解的定义.

定义2.1对于任意的ε ＞0，如果有

成立，那么us（x），s ＝1，2，n是式（2）的ε－近似解.

定理2.2对于任意的ε ＞0，存在N ＞0，当ω ＞N时，

证明设F是一个关于cs，k，s ＝1，2，…，n，k ＝1，2，…，ω 的二次型，

下面采用配置法去获得式（2）的ε 近似解.

然后给出式（4）的矩阵形式

其中

其中s ＝1，2，…，n，k ＝1，2，…，ω.

根据定理2.5，很容易就可以得到方程组（2）的近似解us，ω(x )，s ＝1，2，…，n，k ＝1，2，…，ω.

定理2.6假设us(x )是方程组（2）的精确解，us，ω(x )，s ＝1，2，…，n，k ＝1，2，…，ω 是方程组（2）的近似解，则us，ω(x )一致收敛于us(x ).

定理2.7假设us(x )是方程组（2）的精确解，us，ω(x )，s ＝1，2，…，n，k ＝1，2，…，ω 是方程组（2）的近似解.如果每个( x)在区间［0，1］上是有界的，那么

3 数值算例

例1 考虑以下线性积分微分方程组问题［1 8］

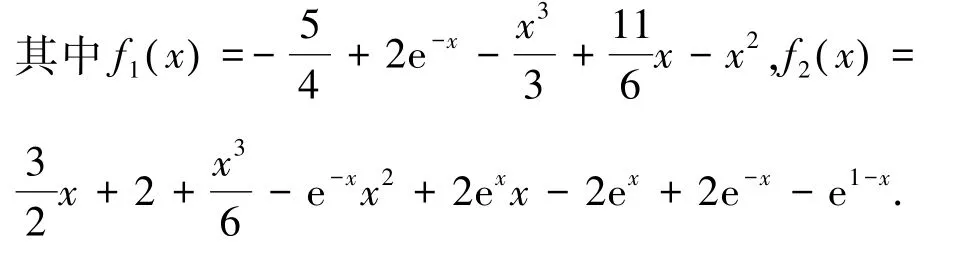
方程组的精确解为u1(x ) ＝x，u2(x ) ＝x2.文献［18］给出了一个计算方程组问题最大绝对误差的公式

文献［18］得到E30＝4.199 ×10－6，在ω ＝6，τ ＝10时，该文计算的结果为E6＝1.110 ×10－15.其他数值结果见表1和如图1所示.

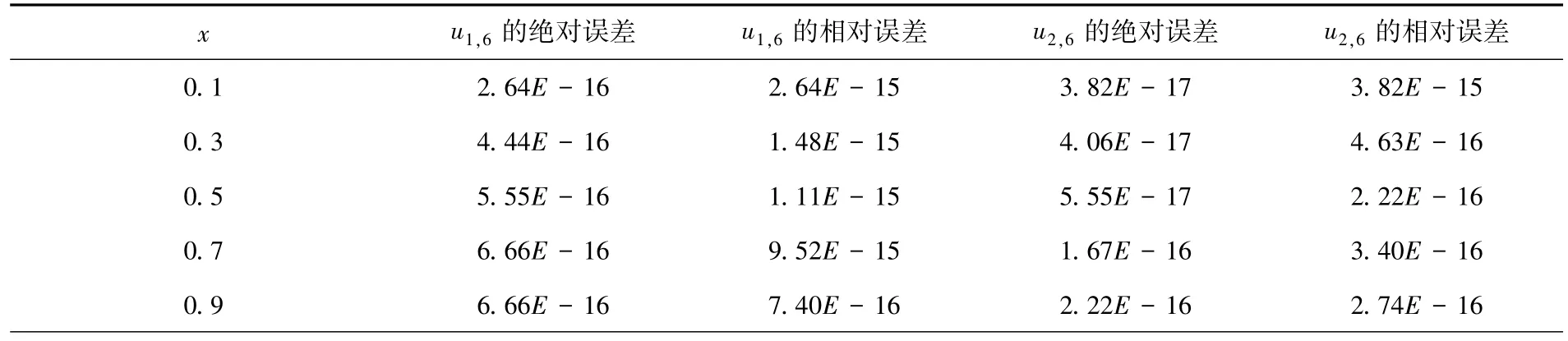
表1 例1近似解的绝对误差与相对误差

表2 例2中近似解在ω 不同取值下的最大绝对误差

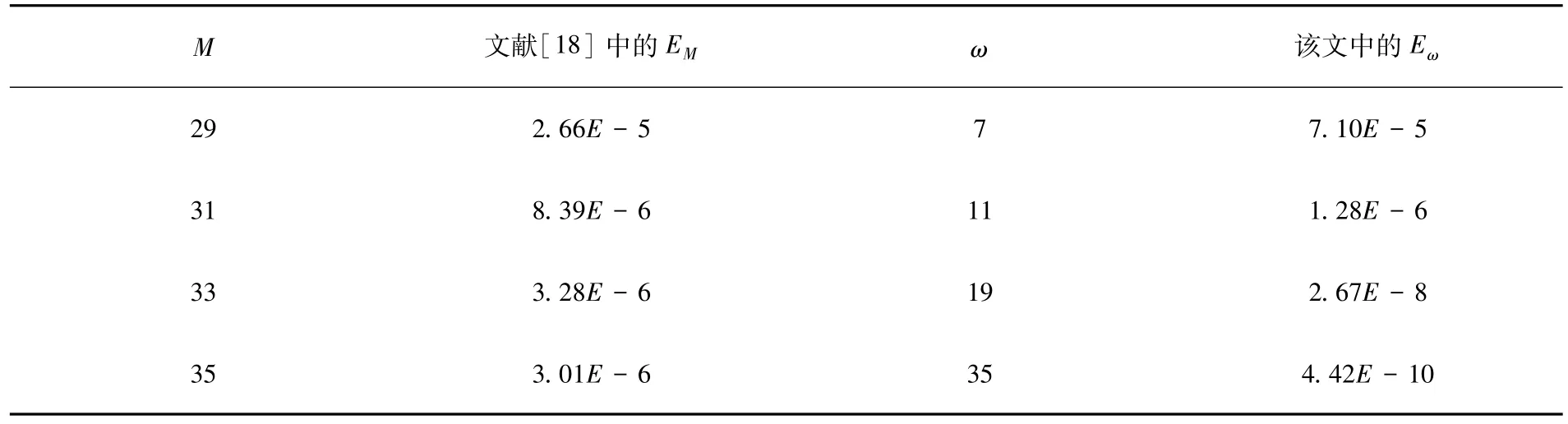
表3 例2中近似解的最大离散范数

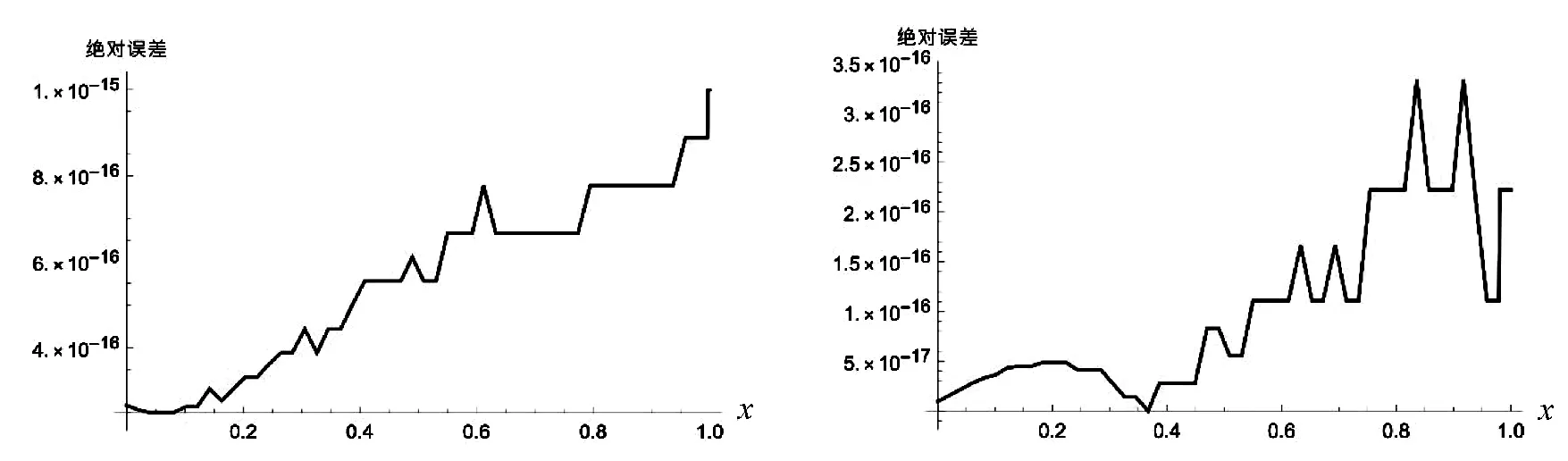
图1 例1中近似解u1，6 的绝对误差（左）及近似解u2，6 的绝对误差（右）

例2考虑以下线性积分微分方程组问题［18］