极坐标系解题的优劣之小议

■四川省绵阳实验高级中学 李小侠

在整个高中数学知识的学习中,极坐标虽然作为高考的选考内容之一,但是由于它相对比较简单,因此,在考试时很多同学都会选择极坐标一题。本文就极坐标的作用及优劣势做一些总结,以便同学们在学习和考试中能少走些弯路。

一、极坐标方程与直角坐标方程的互化

例1已知极坐标系的极点与平面直角坐标系的原点重合,极轴与x轴的非负半轴重合,在极坐标系中,若直线l的极坐标方程为

(1)求直线l的直角坐标方程;

评注:对于同学们来说,只要把平面直角坐标和极坐标互化的公式记住,一般情况下,解答知一求另一的题目都不成问题。

二、求两条曲线的交点问题,直角坐标与极坐标的优劣对比

解析：(1)法一:先将曲线C2与曲线C3的极坐标方程化为直角坐标方程,联立方程,解出交点坐标即可。

法二:可以直接联立曲线C2与曲线C3的极坐标方程,解出交点的极坐标形式,然后化为直角坐标即可。知,它们还有一个交点是极点(0,0),所以用极坐标联立求解就很容易漏解或增解,因此,需通过图像进行补漏,所以两条曲线的交点的极坐标为(0,0)和,化为直角坐标为(0,0)和

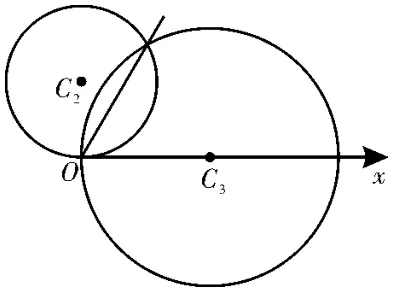
图1

(2)将曲线C1化为极坐标方程,分别与曲线C2,C3的极坐标方程联立,解出点A,B的极坐标,利用两点间的距离公式进行计算,结合三角函数的辅助角公式化简得最大值。

评注:通过该题我们不难发现,如果题目告诉的全是极坐标方程,求的也是极坐标方程,那么我们用极坐标方程联立求解即可,比化成直角坐标方程求解后再化回来要简单得多。如果告诉的是极坐标方程,求的是直角坐标方程,那么我们从一开始就化成直角坐标方程进行联立求解,一是大多数同学比较熟悉直角坐标方程,二是可以避免出现漏解或增解的问题。但无论采取哪种方法求解,都必须注意范围限制,必要时可以依赖图形避免失误。

评注:像本题这种有范围限制的话,直接用极坐标方程联立求解曲线交点问题就比较方便,而用直角坐标方程联立就要绕一个大圈,因此两种方法各有优劣,我们应根据题目的已知来选取合适的方法。

三、依据极坐标系中极径和极角的几何意义求解题目

例4过 极 点O作 圆C:ρ=8cosθ的弦ON,求ON的中点M的轨迹方程。

解法一：由题得圆C的直角坐标方程为(x-4)2+y2=16,所以圆心坐标为(4,0),半径为4。在极坐标系中作出圆C的图像,如图2 所示,圆心C（4,0 ）,半径,连接CM,因为M为弦ON的中点,所以CM⊥ON,所以M在以OC为直径的圆上。此时可以直接写出极坐标方程,也可以先写出直角坐标方程再化成极坐标方程。故动点M的轨迹方程是ρ=4cosθ（ρ≠0）。因为题中说有弦ON存在,所以要有条件限制ρ≠0。

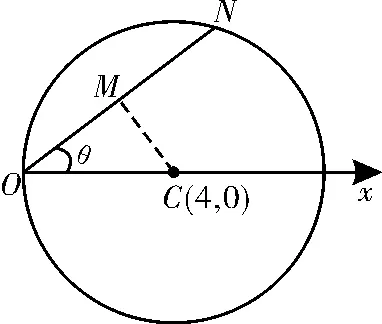
图2

解法二：把圆的极坐标方程化为直角坐标方程为x2+y2=8x,设中点M(x,y),由于M为ON的中点,所以N(2x,2y),而N点在圆上,代入圆的方程得(2x-4)2+4y2=16,再化为极坐标方程,可得动点M的轨迹方程为ρ=4cosθ（ρ≠0）。同样要有限制条件ρ≠0。

评注:本题主要考查动点的轨迹方程,以及极坐标和直角坐标的互化,重要的是结合图形,翻译出动点的几何意义,无论用哪种坐标系写出动点的轨迹方程都比较简单,意在考查同学们对这些知识的理解掌握水平和分析推理能力。

(1)求曲线C1的极坐标方程和曲线C2的直角坐标方程;

评注:本题的第二问如果用平面直角坐标方程来求解,先要把极坐标化为直角坐标,然后联立求解,还要用到距离公式,才能算出三角形的面积。如果根据极径和极角的几何意义,先联立极坐标方程,求出两点的极坐标,再根据三角形的面积公式即可解决问题,公式中的边长由极径来担任,公式中的角度由OA,OB两条极径之间的极角之差来解决,这道题目就显得非常简单。

总之,我们在遇到有关极坐标中的边角问题时,要有意识地往极坐标上去想,而不能觉得平面直角坐标系熟悉,一味地往平面直角坐标上面转化,总想用自己熟悉的思想方法去解决问题,结果反而使问题复杂化。