减震橡胶材料的两种等双轴拉伸测试方法对比研究

赵义东 葛琪

摘要 文章通过对两种不同的双轴拉伸试验机进行了基于圆形试样和方形试样的等双轴拉伸测试对比試验，以探究减震橡胶材料的等双轴拉伸测试。试验结果表明，两种测试方法都能够实现高应变水平的等双轴拉伸测试，且基于方形试样的等双轴拉伸测试可达到的应变水平更高。文章还通过有限元方法验证了两种测试方法的临界应变水平，为试验设计提供了重要参考。

关键词 橡胶材料；等双轴拉伸；圆形试样；方形试样；临界应变水平

中图分类号 TQ332文献标识码 A文章编号 2096-8949（2023）11-0026-03

0 引言

橡胶材料因其突出的高弹性，广泛应用于各类交通工具的减震器中。独特的橡胶配方是减隔震产品的核心竞争力之一，而对应的超弹和疲劳性能测试则是检验配方性能的一种重要手段。目前，橡胶材料的基本力学性能主要通过单轴拉伸、平面剪切、双轴拉伸测试进行探究。其中，双轴拉伸测试等效于单轴压缩测试，是表征橡胶材料在复杂应力状态下力学行为的一项关键测试，已有国内外学者进行了大量的理论和实验研究。Mansouri、Attila Bojtos等[1-2]通过橡胶圆形薄膜膨胀试验，实现了小区域内等双轴拉伸状态下的机械性能测量。Diani[3]等通过一种新型的平面双向拉伸加载机构，实现了在任意平面试样上产生等双向或非等双向拉伸状态，但具有夹具难以调整和只能同比例双向拉伸等问题。周华森等利用有限元分析软件模拟十字形试样进行等双轴拉伸测试，得到了应力应变分布最均匀的试样型。张选利等基于带有半圆形切口的十字形试样，在加载臂处进行开臂缝设置，在中心测试区域获得了较好的均匀变形拉伸响应，但难以实现大应变水平的双轴拉伸状态。刘国均等介绍了基于圆形试样的等双轴拉伸试验设备及试验方法：将圆形切口试样用夹子通过16根高强度钢索向外等量移动，但对于夹具和钢索控制精度要求很高。张墨昊等基于Zwick/Roell卧式平面双轴拉伸材料试验机自行设计了双轴拉伸夹具，完成了硅橡胶的双轴拉伸大变形测试。德国Coesfeld公司设计了一种新型双轴平面拉伸试验装置，以四台电机独立控制四个方向上的拉伸变形，配合专用的夹具和方形试样，实现了中间观测区域的高应变水平双轴拉伸状态。

该文通过对基于圆形试样和方形试样的橡胶材料双轴拉伸测试进行对比试验，分析其应力应变状态，并进行相应的有限元分析，得到了两种测试方法的临界应变水平。

1 试验对比研究

1.1 试验装置及试样基本情况

该文采用Test Resources双轴拉伸试验机对圆形试样进行加载。圆盘式的结构设计是利用1台电机同时驱动钢索对样品的16个方向进行等力拉伸。圆形试样尺寸为Φ60 mm×2 mm，对应的主机结构和试样几何结构见图1。圆形试样和方形试样均采用相同配方、相同硬度的胶料。

相应地，该文采用Coesfeld双轴拉伸试验机对方形试样进行加载，其采用4台电机同时驱动夹具对样品的4个方向同时进行拉伸，对应的主机结构和试样见图2。方形试样尺寸为76.8 mm×76.8 mm，厚度为1.8 mm，在试样边缘有防止挤压变形的圆柱状夹持端。

1.2 试验内容及数据采集

对基于两种试样的双轴拉伸测试的基本试验内容设置见表1。

对于圆形试样，在定义名义应力时，可由下式给出：

式中，F——径向载荷合力；D——试样的有效直径；t——试样的初始厚度；σ为名义应力。

采集圆形试样的应变时，由于夹具在径向的位移量与试样中心区域的名义应变无确定关系。因此，利用非接触式视频采集系统测量中心区域的名义应变。

对于方形试样，方形试样在采集应力应变数据时，名义应力可由下式给出：

式中，F——x或y方向的载荷合力；A——试样在x或y方向的有效截面积；t——试样的初始厚度；σ——名义应力。

方形试样的名义应变同样由非接触式视频采集系统提供。

1.3 试验结果分析

通过试验得到了两种试样在不同应变水平下的应力应变曲线，选取50%、100%应变水平的第五次加载曲线，得到等双轴拉伸应力应变曲线见图3。实验结果表明，同一种材料在两种测试方法中的不同应变水平下的应力应变曲线较为吻合。

图3 两种试样在50%、100%应变水平下的

等双轴拉伸应力应变试验曲线

此外，在基于圆形试样的等双轴拉伸测试过程中，应变水平达到100%时，有2个试样发生破坏，而在基于方形试样的等双轴拉伸测试过程中则无此类状况。分析其原因，圆形试样在中心区域应变水平达到100%及以上时，拉伸臂处易发生断裂，导致测试中断。

2 基于试验的仿真对比分析

2.1 有限元模型及载荷设置

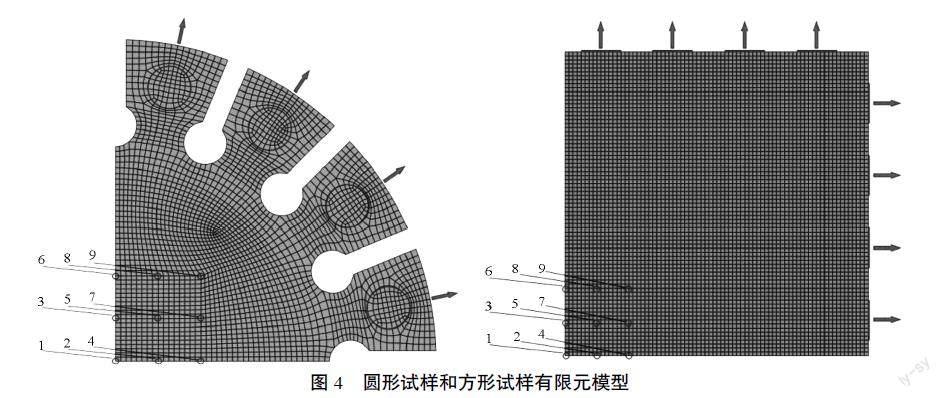
根据该文已进行的试验，建立有限元模型进行仿真分析。图4即是圆形试样和方形试样的有限元网格模型（利用对称性建立1/4模型）。模拟夹具对于试样的作用，对圆形试样进行径向加载30.25 mm，对方形试样沿x和y方向加载38.0 mm。

2.2 有限元仿真结果分析

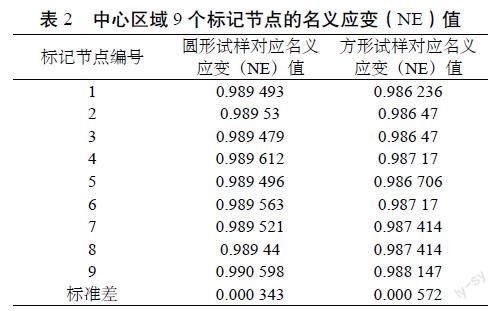
在中心区域（8 mm×8 mm）范围内，对两种试样的9个对应位置进行节点标记，取应变值见表2。引入标准差来评估9个标记节点名义应变（NE）值的离散程度，可以发现圆形试样和方形试样中心区域的变形都较为均匀，且圆形试样均匀性略好于方形试样。

选取两种试样中心区域应变值为100%时的应力云图如图5所示，分析结果表明：在相同应变水平（中心区域名义应变为100%）下，圆形试样的最大应力为20.17 MPa，应力最大值位于拉伸臂处（图5标记圈中），方形试样的最大应力为17.88 MPa，应力最大值位于试样边缘。与已有试验结果结合分析，随着中心区域的名义应变增大到100%，圆形试样在拉伸臂处应力最大，且拉伸臂两侧缺口由刀具压制而成，可能存在初始缺陷，易发生断裂，而方形试样的应力最大处位于试样边缘的加厚区域，不易断裂。

选取两种试样中心区域应变值为150%時的应力云图进行对比，可以得到圆形试样在拉伸臂处的最大应力为42.06 MPa，方形试样在试样边缘的最大应力为39.39 MPa。按照测试的橡胶材料的最大拉伸强度为30 MPa来计算，圆形试样的拉伸臂已经完全破坏，方形试样的边缘发生部分破坏。分析破坏产生的影响，圆形试样在拉伸臂处发生断裂即测试中断，方形试样在边缘处发生断裂仍能继续测试，可以推断方形试样能够完成更高应变水平（150%）的等双轴拉伸测试。

3 结论

根据试验以及有限元分析结果，形成以下结论：

（1）基于圆形试样和方形试样的等双轴拉伸测试都能够有效地反映出橡胶材料在等双轴拉伸状态下的应力应变行为，测试效果良好。

（2）两种试样中心区域在高应变（100%）下的应变分布都较为均匀，且圆形试样均匀性略好于方形试样。

（3）高应变水平下，对于同种橡胶材料，圆形试样在拉伸臂处应力最大，易发生断裂，而方形试样的应力最大处位于试样边缘的加厚区域，不易断裂。方形试样相较于圆形试样能够达到的应变水平更高，推断其能够完成150%应变水平的等双轴拉伸测试。

参考文献

[1]M. R. Mansouri， H. Darijani， M. Baghani. On the Correlation of FEM and Experiments for Hyperelastic Elastomers[J]. Experimental Mechanics， 2017（2）： 195-206.

[2]Attila Bojtos， Antal Huba， Lena Zentner， etal. Measuring of Equibiaxial Tension of Rubber-Like Materials by Optical Method[J]. Materials Science Forum， 2010（659）： 289-294.

[3]M. Brieu， J. Diani， N. Bhatnagar. A New Biaxial Tension Test Fixture for Uniaxial Testing Machine - A Validation for Hyperelastic Behavior of Rubber-Like Materials[J]. Journal of Testing and Evaluation： A Multidisciplinary Forum for Applied Sciences and Engineering， 2007（4）： 364-372.