水泥混凝土路面板几何形状对力学性能分析
2023-06-29高武袁玲
高武 袁玲


采用单一控制变量的方法,分析矩形水泥混凝土路面板和六角形水泥混凝土路面板的力学性能。即只改变路面板的几何形状,不改变路面板的材料、长度、宽度、厚度等因素。通过Midas fea软件进行加载和模拟,得出六角形水泥混凝土路面板在位移、应变、应力等力学指标上具有优越性。
水泥混凝土路面板; 几何形状; 力学性能; Midas fea
U416.2 A
[定稿日期]2022-05-23
[基金项目]2021年省级大学生创新创业训练计划项目(项目编号:S202110879023);安徽科技学院校级科研项目(项目编号:2021zryb14)
[作者简介]高武(1999—),男,本科,研究方向为土木工程。
[通信作者]袁玲(1986—),女,硕士,讲师,研究方向为道路工程教学与科研。
1 建模流程
1.1 前期材料的收集
孙增华[1]针对水泥混凝土路面出现了复杂断板和寿命不及预期等问题,分析了路面板早龄期性状与长期温度场以及交通荷载共同作用下路面板的力学行为,揭示了早龄期性状对路面板破坏行为的影响。赵亚兰、陈拴发[2]针对近年来农村公路水泥混凝土路面结构中出现的主要病害问题,提出了小板块水泥混凝土路面板几何尺寸效应的概念,对一种农村公路水泥混凝土路面典型结构进行温度应力分析,总结了小板块水泥混凝土路面板平面尺寸对其自身温度应力的影响规律。两者都进行了温度应力的研究,但是有关于路面板几何形状的分析却很少。
1.2 中期相关参数的选定
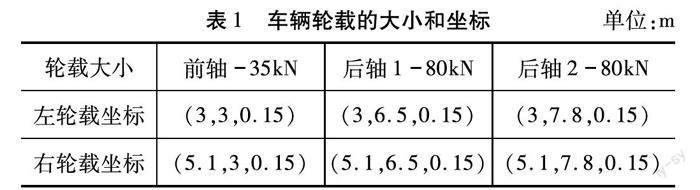
选定路面为汽车专用二级公路,即选择标准宽度为9 m的公路[3],采用公路长度为10 m。车辆轮载的加载地点都选择在同一处,大小、方向都相同。表1为施加车辆轮载的坐标(适用于WCS坐标系)。对于矩形水泥混凝土路面板的几何尺寸:其长度和宽度都为1 m,厚度为0.15 m[4]。对于六角形水泥混凝土路面板的形状及几何尺寸:其平面形状为正六边形,长度为1 m,厚度为0.15 m。对于路面板材料,都选择等级为C25的混凝土。由于路面板以及模拟的公路长度都较小,故采用普通水泥混凝土路面,也就是素混凝土路面。因此,板内不配筋。为了更好分析矩形水泥混凝土路面板和六角形水泥混凝土路面板的力学性能,将路面板之下的土层假定为极密实土中的人工压实的填亚黏土。因为所加的竖向荷载对试验结果影响大,查阅相关规范,x、y 2个方向的地基反力模量Kx、Ky选为1 000 kN/m3,模拟的地基土在z方向的地基反力模量Kz为100 000 kN/m3。
1.3 后期建模步骤
首先要进行实体的创建。对于矩形实体的创建比较简单,输入箱型的几何尺寸以及角点的空间直角坐标,即可得到需要的矩形实体。而对于六角形实体的创建比较复杂,首先用2D多边形生成一个正六边形面,选定角点的空间直角坐标,然后根据厚度数值扩展生成一个实体。以上步骤仅仅生成一个实体,共计需要90个矩形实体和36个六角形实体。此时可以按照上述方法一一建立,也可以用复制命令,分别输入复制距离沿x、y 2个方向的空间坐标。采用后者方法建立所有实体更为简单。第二步要进行材料的创建与修改。在材料数据库中选择“JTG04(RC)_C25”,Midas fea软件自动导出C25等级混凝土的弹性模量、重量密度、泊松比等信息。为简化模型,本构模型设置为弹性,忽略材料温度依存特性、时间依存特性。第三步是进行网格划分。在Midas fea建模中,网格划分是最为重要的一步。网格划分精度较高时,其计算结果的精度一般也较高。由于矩形板是规则的六面体,因此采用自动实体网格进行划分(六面体主导)。而六角形板是较为规则的几何体,因此采用自动实体网格划分。两者划分的单元尺寸均为0.1 m。在网格划分的同时,将材料特性赋给实体,此时的实体才是实际工程上的水泥混凝土路面板。第四步是边界条件的确定。由于已提前假定地基土为极密实土中的人工压实的填亚黏土,便于模拟水泥混凝土路面板实际的受力,选择在矩形水泥混凝土路面板和六角形水泥混凝土路面板与土层接触的面上建立点弹簧。而点弹簧正是模拟地基土对路面板的支撑情况。第五步是荷载的施加。本试验的荷载考虑水泥混凝土板的自重和车辆轮载。水泥混凝土板的自重在z方向上对试验影响最大,但是在x、y方向上对试验影响不大,故将自重因子x、y设置为0。而自重因子z与坐标系规定的z方向相反,故将自重因子z设置为-1。对于车辆轮载,前面已经阐述,不再赘述。最后一步是分析工况的输入。从2种水泥混凝土路面板的反力、位移、3D单元应变、3D单元应力等来进行力学分析,所以分析类型为线性静力。将组目录数中的所有单元、边界条件、荷载导入到应用中。Midas fea软件计算完成后,即得到所需数据。
2 结果分析
2.1 反力数据对比分析矩形水泥混凝土路面板和六角形水泥混凝土路面板
由于水泥混凝土板自重和汽车荷载的方向都是竖直向下的,故研究z轴方向的反力Fz。从矩形水泥混凝土路面板反力Fz云图中(图1),可以明显看到:车辆轮载作用的小范围面内,反力Fz较大,最大反力Fz达到4.497 36×10-1 kN。反力Fz最小值为-7.258 98×10-3 kN,发生在远离车辆轮载的矩形水泥混凝土路面板上。从六角形水泥混凝土路面板反力Fz云图中(图2),可以明显看出:反力Fz最大值为3.410 37×10-1 kN,其位置也在车辆轮载作用的那个小范围面上。反力Fz最小值为-1.777 50×10-2 kN,也发生在远离汽车荷载的六角形水泥混凝土路面板上。通过上面反力Fz最大值的数据,对比分析得到结论:六角形水泥混凝土路面板的反力Fz最大值明显低于矩形水泥混凝土路面板的反力Fz最大值。从反力数值分布图中,可以明显观察到:模拟路面的矩形水泥混凝土路面板有57.4%是处于较低的数值,即反力Fz从(-7.258 98×10-3 kN, 2.130 32×10-2 kN)的矩形水泥混凝土路面板占了总矩形水泥混凝土路面板的57.4%,已经超过了50%。而六角形水泥混凝土路面板有53.1%是在(-1.025 50×10-2~4.650 75×10-3 kN)。因此矩形板和六角形板在低受力区分布差别不大。并且矩形水泥混凝土路面板和六角形水泥混凝土路面板在经过反力Fz最大百分比区间后,其余反力Fz区间所占百分比并不是一直较小。例如矩形水泥混凝土路面板在经过(-7.258 98×10-3 kN,2.130 32×10-2 kN)之后,仍然有25.9%的矩形水泥混凝土路面板处于(2.130 32×10-2 kN,4.986 54×10-2 kN)这个极小区间。而六角形水泥混凝土路面板在经过(4.650 75×10-3 kN,2.707 65×10-2 kN)之后的一个极小区间(2.707 65×10-2 kN,4.950 22×10-2 kN)时,会有一个较大百分比的分布,分布百分比为22.2%。因此,六角形水泥混凝土路面板的极小区间长度比矩形水泥混凝土路面板的极小区间长度短。即六角形水泥混凝土路面板反力Fz分布得更均勻。因此,综上所述,根据反力Fz进行对比,六角形水泥混凝土板的力学性能优于矩形形水泥混凝土路面板。
2.2 位移数据对比分析矩形水泥混凝土路面板和六角形水泥混凝土路面板
由于车辆轮载的施加,对3个空间方向即x、y、z均有影响,故分别分析3个方向的位移。对于矩形水泥混凝土路面板来说,x方向的位移云图在车辆轮载的作用下形似对称的弯月。在车辆轮载施加点所在的极小平面内,其位移并非满足简单的线性关系。其沿x方向位移的过渡并不明显,即沿x方向的位移图具有突变点。以沿行车方向的2个荷载点所连直线分析,其左边和右边沿x方向位移的数值大小差别不大,但是符号相反。施加荷载越小,其沿x方向的位移图颜色越淡,说明其位移数值也越小。此种定性规律也符合实际工程上的规律。而对于沿y方向的位移,在车辆轮载作用的小范围面上,位移过渡明显,即具有稳定的过渡区。而对于沿z方向的位移,过渡区并不明显。将x、y、z 3个方向的位移进行叠加,得到矩形水泥混凝土路面板的实际位移云图(图3)。从图中可以明显看到:其实际位移云图与沿z方向的位移云图形状相似,显著的差别是数值不同。对于六角形水泥混凝土路面板来说,沿x方向、y方向、z方向的3个位移云图,与矩形水泥混凝土路面板的位移云图类似。略微有所不同的就是在沿z方向位移图中,矩形水泥混凝土板在对称的80 kN汽车荷载中央并无联系。但是对于六角形水泥混凝土路面板则与之相反,在对称的80 kN汽车荷载中央似乎有一条像纽带的东西连接着左、右2个位移区。即在六角形水泥混凝土路面板对称的80 kN汽车荷载中央处,六角形水泥混凝土路面板沿z方向的位移均匀变化。而对于x、y、z 3个方向叠加的实际位移(图4),在对称的80 kN汽车荷载中央也有一条像纽带的东西,即实际位移在车辆轮载较大处,位移变化比较均匀,不会有突变点。
从数值分析:对于沿x方向的位移,矩形水泥混凝土路面板的最大位移为2.557 95×10-5 m,而对于六角形水泥混凝土路面板的最大位移为1.933 35×10-5 m,明显看出:六角形水泥混凝土路面板沿x方向的位移小。对于沿y方向的位移,矩形水泥混凝土路面板的最大位移为2.730 43×10-5 m,而对于六角形水泥混凝土路面板的最大位移为1.933 35×10-5 m,可以看出:六角形水泥混凝土路面板沿y方向的位移也较小。对于沿z方向的位移,矩形水泥混凝土路面板的最大位移为1.453 16×10-5 m,而对于六角形水泥混凝土路面板的最大位移为2.662 98×10-5 m,仅从数值分析沿z方向的位移,矩形板水泥混凝土路面的位移小。对于沿x、y、z 3个方向的实际位移,矩形水泥混凝土路面板的最大实际位移为4.864 67×10-4 m,而对于六角形水泥混凝土路面板的最大位移为4.116 89×10-4 m。综上所述:六角形水泥混凝土路面板在沿x方向、y方向以及沿x、y、z 3个方向的实际位移都较小。因此从位移大小以及分布角度来对比矩形水泥混凝土路面板和六角形水泥混凝土路面板、六角形水泥混凝土路面板具有一定的优势。
2.3 3D单元应变、应力数据对比分析矩形水泥混凝土路面板和六角形水泥混凝土路面板
水泥混凝土路面板的应变、应力有很多种,这里只分析Exy、Sxy。从矩形水泥混凝土路面板的应变云图(图5)可以看到:其路面板Exy最大值為6.310 87×10-5,Sxy最大值为7.362 68×102。从六角形水泥混凝土路面板的应变云图(图6)可以看到:其路面板Exy最大值为3.834 11×10-5,Sxy最大值为4.473 13×102。仅从数值分析,六角形水泥混凝土路面板Exy、Sxy最大值接近矩形水泥混凝土路面板Exy、Sxy最大值的一半。而从分布角度来分析,矩形水泥混凝土路面板的Exy有70.3%处于(-7.841 52×10-6,7.925 20×10-6)。而六角形水泥混凝土路面板的Exy有84.5%处于(-7.574 10×10-6,1.608 94×10-6)。因此,六角形水泥混凝土路面板的Exy、Sxy在较小区间内分布得较多。即在小应变、应力区间内,六角形水泥混凝土路面板所占较多。因此从应变、应力大小以及分布角度来对比矩形水泥混凝土路面板和六角形水泥混凝土路面板,六角形水泥混凝土路面板具有一定的优势。
3 结论
路面工程大多采用矩形水泥混凝土路面板,少数采用六角形水泥混凝土路面板。从经济、工厂预制难易性方面考虑,矩形水泥混凝土路面板具有优势。但在路基路面工程中,路面板的受力也是需要考虑的问题。通过Midas fea软件模拟,从位移、应力、应变角度分析,六角形水泥混凝土路面板在力学特性上具有优越性。
参考文献
[1] 孙增华.基于早龄期理论的水泥混凝土路面板力学响应分析[J].福建交通科技,2021(10):1-8.
[2] 赵亚兰,陈拴发.小板块水泥砼路面温度应力数值分析[J].公路与汽运,2011(1):78-81.
[3] 徐敏,王仲硕,程建川,等.二级公路断面型式分析[J].中外公路,2004(1):52-54.
[4] 黄晓明.路基路面工程.第六版[M].北京: 人民交通出版社股份有限公司,2019.
