大跨铁路钢桁梁柔性拱桥地震响应和阻尼器参数优化研究

2023-06-29陈婧雯郑凯锋左志超

四川建筑 2023年2期

陈婧雯郑凯锋左志超

以（138+2×360+138）m大跨铁路连续钢桁梁柔性拱桥设计方案为工程背景，建立考虑桩土共同作用的有限元分析模型，采用非线性时程分析法研究其在不同地震组合作用下的地震空间响应，并优化分析其阻尼器参数。研究结果表明：在地震水平两方向组合作用下桥梁的内力响应较单向作用的大，竖向地震作用对桥梁内力和位移影响均较小，对该类拱桥的抗震验算可不计竖向地震作用，仅需考虑地震水平向组合作用。设置纵向粘滞阻尼器后，各墩墩底弯矩明显减小，拱脚轴力有所减小，墩梁相对位移也明显减小。综合选取最优阻尼器参数组合后，墩底弯矩减小58.59%，拱脚轴力减小19.1%，墩顶拱肋最大弯矩值减小50.7%，墩梁相对位移减小74.9%。

铁路桥梁；地震响应；有限元分析；钢桁梁柔性拱桥；时程分析；粘滞阻尼器

U442.5+5 A

［定稿日期］2022-01-10

［作者简介］陈婧雯（1997—），女，硕士，研究方向为现代桥式及桥梁结构设计理论。

钢桁梁柔性拱桥受力明确，结构较为新颖，造型美观，是目前大跨度铁路桥梁常用桥型之一。随着我国铁路建设事业的蓬勃发展，我国已建成多座铁路钢桁梁柔性拱桥，如合福铁路南环线南淝河大桥、京沪高铁济南黄河大桥、厦深铁路榕江特大桥等。

近年来已有许多学者对大跨度钢拱桥的抗震性能进行了研究［1-5］，探讨了地震波一致激励、行波效应和多点激励、多维激励下的地震响应。研究表明，单一方向的地震动输入会明显低估大跨度钢拱桥的地震响应，大跨度钢拱桥地震动输入模式应考虑三向地震动同时输入［6-7］。行波效应对大跨度上承式钢桁拱桥地震响应有很大影响，但行波地震响应与波速间未发现规律性变化［8］。这些研究大多针对上承式钢桁拱桥、中承式钢管混凝土拱桥、刚性拱肋钢拱桥。目前针对钢桁梁柔性拱桥的研究主要集中于极限承载力［9］、稳定性［10］、施工控制关键技术［11］等方面，对其抗震性能的研究较少。施成等［12-13］计算分析了黄河特大桥在一致和非一致激励作用下的空间地震响应，认为大跨度钢桁拱桥抗震设计应充分考虑地震波的空间和时间效应。刘应龙等［14］以黄河特大桥为例，探讨了粘滞阻尼器各参数对结构地震响应的影响。与传统钢桁拱桥不同，钢桁梁柔性拱桥拱肋刚度相对较小，主要受力构件为钢桁梁，在铁路中应用时多采用双拱或多拱连续体系，跨度也越来越大。因此，有必要对其抗震性能进行专门研究。

本文以（138+2×360+138） m大跨度铁路连续钢桁梁柔性拱桥为研究对象，利用Midas Civil 2020建立考虑桩土共同作用的空间有限元模型，采用非线性时程分析法对该桥在4种不同地震组合作用下的地震空间响应进行分析，并引入纵向粘滞阻尼器，探讨粘滞阻尼器参数对其地震空间响应的影响规律，综合选取最优的阻尼器参数组合，以期为类似桥梁的抗震设计提供一定的参考价值。

1 计算模型

1.1 工程概况及有限元模型

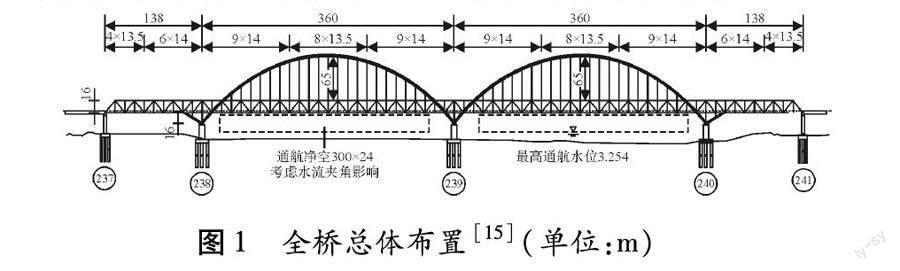
某双线铁路大跨度下承式连续钢桁梁柔性拱桥跨径布置为（138+2×360+138） m，拱肋拱轴线为二次抛物线，结构总体布置如圖1所示。239号中主墩为固定墩，两个边主墩及连接墩为纵向活动横向固定墩。利用Midas Civil 2020建立全桥有限元模型。主桁及拱肋杆件采用梁单元模拟，柔性吊杆采用桁架单元模拟。全桥共计8 159个单元，5 268个节点。支座采用弹性连接处理，土对桩基础的作用用等效弹簧模拟，用TB10002.5—2005《铁路桥涵地基与基础设计规范》［16］中的“m”法计算土弹簧刚度。二期恒载采用梁单元荷载施加在纵梁上，将自重和二期恒载转换为质量。

1.2 地震动参数

桥址处基本地震动峰值加速度为0.10g，地震动反应谱的特征周期为0.60 s。非线性时程分析时地震波选取有代表性的EL Centro波，依据GB 50111-2009《铁路工程抗震设计规范》［17］以及桥址区场地特征，保持其频谱特性，调整其加速度峰值为罕遇地震动峰值加速度2.06 m/s2，修正后的纵向时程曲线如图2所示。

分析4种地震组合作用下桥梁的空间地震响应。4种地震组合作用分别为：组合1纵向地震作用；组合2横向地震作用；组合3纵向+横向组合作用；组合4纵向+横向+65%竖向地震组合作用。

2 自振特性分析

基于全桥有限元模型，采用多重Ritz向量法对该桥进行结构自振频率与振型特征分析。提取前10阶振型的自振周期与振型特征，见表1。计算各方向前100阶振型时，其三向振型参与质量均达到总质量的90%以上。本桥对应的主振型为拱梁横向弯曲，说明该桥横向抗震不利。

3 地震响应分析

3.1 内力响应

非线性时程分析结果表明，4种不同地震组合作用下拱肋的内力响应大于主桁。不同地震组合作用下拱肋截面轴力和弯矩如图3、图4所示。

不同地震组合作用下，拱肋的轴力在239号固定墩拱脚处最大。在组合3作用下，239号固定墩拱脚处轴力达到26 844 kN，是组合1作用下的1.6倍，组合2作用下的1.3倍。拱肋的弯矩最大值出现在239号固定墩顶拱肋与下弦相交节点处。在组合3作用下，239号固定墩顶拱肋弯矩达到4 852 kN·m，是组合1作用下的1.02倍，组合2作用下的6.13倍。相比地震单向作用，地震水平两方向组合作用下桥梁的内力响应更大。一些论文按GB 50111-2019《铁路工程抗震规范》［17］进行抗震验算时，仅考虑纵向地震单向作用和横向地震单向作用，偏于不安全，建议该类拱桥的抗震设计应充分考虑地震水平组合作用。

3.2 位移响应

拱肋与主桁的位移响应趋势一致，刚度相对主桁较小，地震作用下的位移响应更大，沿239号固定墩大致呈对称分布。在4种地震组合作用下拱肋的3方向位移响应结果如图5所示。

由图5可知：

（1）拱肋最大纵向位移出现在1/4拱肋处，在组合4作用下达到127 mm。

（2）横向地震作用时，拱肋横向位移在拱顶处达到最大值449 mm，是最大纵向位移的3.5倍；纵向地震作用几乎不产生横向位移。

（3）拱肋的竖向位移由纵向地震作用主导，组合3作用下在1/4拱肋达到最大值134 mm。

3.3 竖向地震作用影响

由图3、图4可知，拱肋各关键截面轴力在组合3和组合4作用下的拱肋各关键截面轴力图和拱肋各关键截面弯矩图基本重合，竖向地震作用对该桥的内力响应影响很小。从图5可以看出，在组合3和组合4作用下，拱肋各关键截面纵向位移、横向位移以及竖向位移也基本重合，竖向地震作用对3个方向的位移几乎不产生影响。为简化计算，对该类桥梁抗震验算时可不计入竖向地震作用。

4 粘滞阻尼器参数优化

4.1 阻尼器布置及参数组合

239号固定墩墩顶结构的地震响应较大，为改善结构在地震作用下的受力情况，在该桥每个墩的支座旁设纵向粘滞阻尼器，使得桥梁上部结构传递给桥墩的力能够合理地分配到多个桥墩上。粘滞阻尼器的力学计算模型可表达为式（1）。

F=C·vζ （1）

式中：F为阻尼力；C为阻尼系数；v为速度，ζ为阻尼指数。粘滞阻尼器采用Maxwell模型来模拟。

为探讨粘滞阻尼器参数对该连续钢桁梁柔性拱桥抗震性能的影响，确定最优的纵向粘滞阻尼器参数组合，采用非线性时程分析法分别计算采用不同C和ζ组合下的桥梁地震响应，与采用普通支座时桥梁的地震响应进行对比，分析不同阻尼器参数组合的减震效果。地震作用采用“纵向+横向”组合作用。不同阻尼器参数组合见表2。

4.2 阻尼器参数分析

由前面内力响应和位移响应可知，该桥结构对称，地震响应也呈现大致对称趋势，故取该桥237号墩～239号墩跨内的桥梁地震响应进行阻尼器参数分析。阻尼器各参数与桥梁墩底弯矩、拱脚轴力、拱肋弯矩、墩梁纵向相对位移之间的变化关系曲线如图6～图9所示。

由图6可知，与未使用粘滞阻尼器时桥梁的地震响应进行对比，使用粘滞阻尼器后，237号、238号、239号墩墩底弯矩明显减小。237号墩墩底弯矩值随阻尼指数ζ增大而增大，随阻尼系数C增大而减小；当ζ=0.3，C=9000 kN·（s/m）-ζ时，237号墩墩底弯矩减震效果最佳，减小了60.6%。当ζ=0.3、0.5时，238号、239号墩墩底弯矩值随阻尼系数C增大而增大；当ζ=0.7、0.9时，238号、239号墩墩底弯矩值随阻尼系数C增大而呈现先减小后增大的变化趋势。当ζ=0.3，C=3000 kN·（s/m）-ζ时，238号墩墩底弯矩减震效果最佳，减小了41.5%。当ζ=0.7，C=5000 kN·（s/m）-ζ时，239号墩墩底弯矩减震效果最佳，减小了34.1%。

从图7可以看出，不同的阻尼参数组合均能减小238号、239号墩拱脚轴力值。对于238号墩拱脚，轴力值随阻尼系数C增大而减小，随阻尼指数ζ增大而增大；当ζ=0.3，C≥5000 kN·（s/m）-ζ，拱腳轴力变化不明显；当ζ=0.5，C=9000 kN·（s/m）-ζ时，238号墩拱脚轴力减小达19.8%。对于239号墩拱脚，当ζ=0.3、0.5时，轴力值随阻尼系数C增大而减小；当ζ=0.3，C=9000 kN·（s/m）-ζ时，239号墩拱脚轴力减小达8.2%。

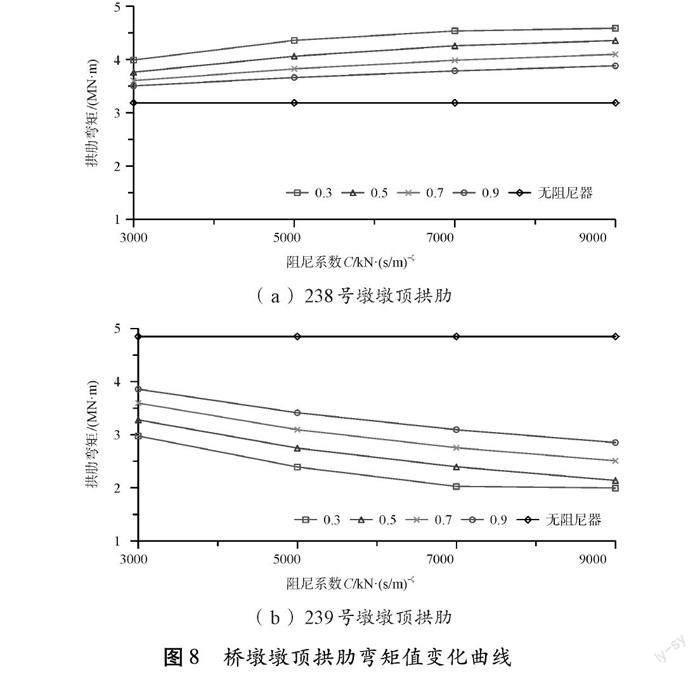
未使用粘滞阻尼器时，拱肋最大弯矩值出现在239号墩墩顶拱肋与下弦相交处，为4.85 MN·m。图8表明，使用粘滞阻尼器后，239号墩墩顶拱肋最大弯矩值明显减小，最优减小59.8%，238号墩墩顶拱肋最大弯矩值有所增加，最大增加30.5%；除ζ=0.3，C=9000 kN·（s/m）-ζ组合外，其余阻尼器参数组合下，拱肋最大弯矩值均出现在238号墩墩顶拱肋与上弦相交处。对于238号墩墩顶拱肋，最大弯矩值随阻尼系数C增大而增大，随阻尼指数ζ增大而减小。对于239号墩墩顶拱肋，最大弯矩值随阻尼指数ζ增大而增大，随阻尼系数C增大而减小。

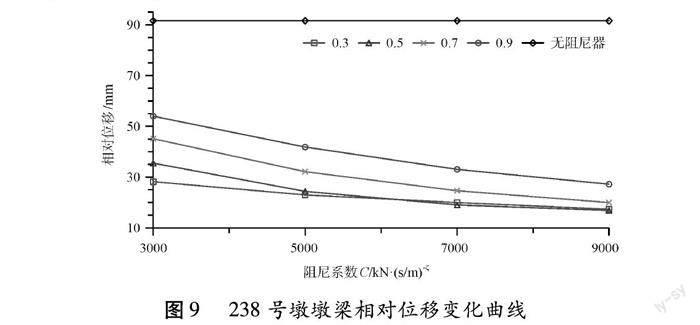
由图9可知，使用粘滞阻尼器后可以显著减小238号墩墩梁相对位移。当ζ一定时，238号墩墩梁相对位移随阻尼系数C增大而减小。当ζ=0.3、0.5，C≥5000 kN·（s/m）-ζ时，238号墩墩梁相对位移变化不大。当ζ=0.5，C=9000 kN·（s/m）-ζ时，238号墩墩梁相对位移减震效果最优，减小了81.0%。

4.3 最优阻尼器参数组合减震效果

综合不同阻尼系数C、阻尼指数ζ对墩底弯矩、拱脚轴力、拱肋弯矩、墩拱相对位移的影响，选取最优阻尼参数组合为C=5000 kN·（s/m）-ζ，ζ=0.3，对各控制变量的减小程度如表3所示。

布置粘滞阻尼器后237号墩、238号墩以及239号墩的墩底弯矩分别减小 58.6%、27.9%和33.2%。全桥墩底最大弯矩值仍出现在239号墩，为594.4 MN·m，与未布置阻尼器时的最大弯矩值889.73 MN·m 相比减震效果明显。238号墩、239号墩拱脚轴力分别减小19.1%、4.1%。尽管238号墩墩顶拱肋最大弯矩值增加17.9%，但239号墩墩顶拱肋最大弯矩值减小50.7%。布置阻尼器前，238号墩墩梁相对位移为91.60 mm，布置阻尼器后其相对位移为22.99 mm，减小74.9%。

5 结论

（1）自振特性分析时，该桥前两阶振型为拱梁横向弯曲，且位移响应也表明该桥横向最大位移响应大于纵向最大位移响应，说明该桥横向抗震不利，在设计时应予以重视。

（2）该桥内力响应最大值出现在239号固定墩墩顶处。在地震水平组合作用下，桥梁的内力响应比单向地震作用下的大，地震空间效应不可忽略。竖向地震作用对该桥内力和位移影响均较小，对该类桥梁的抗震验算可不计入竖向地震作用，仅需考虑地震水平向组合作用。

（3）设置纵向粘滞阻尼器后，各墩墩底弯矩和拱脚轴力明显减小，237号墩墩底弯矩最优减小60.6%；拱脚轴力有所减小，238号墩拱脚轴力最优减小19.8%。239号墩墩顶拱肋最大弯矩值明显减小，最优减小59.8%；238号墩墩顶拱肋最大弯矩值有所增加，最大增加30.5%。238号墩墩梁相对位移明显减小，最优减小81.0%。综合分析，ζ较小，C较大时桥梁减震效果最好。

（4）选取最优阻尼器参数组合C=5000 kN·（s/m）-ζ，ζ=0.3在全桥布置后，237号墩墩底弯矩减小58.6%，238号墩拱脚轴力减小19.1%，239号墩墩顶拱肋最大彎矩值减小50.7%，238号墩墩顶拱肋最大弯矩值增加17.9%，238号墩墩梁相对位移减小74.9%。综合分析，该阻尼器参数组合可有效改善该类拱桥的整体抗震性能。

参考文献

［1］赵灿晖，周志祥.大跨度上承式钢桁拱桥的地震响应分析［J］.铁道科学与工程学报，2006（5）：6-11.

［2］戴公连，汪禹.大跨度铁路连续梁拱组合桥梁地震响应特性［J］.铁道科学与工程学报，2015，12（3）：557-563.

［3］夏超逸，钟铁毅.高速铁路南京大胜关长江大桥地震响应分析［J］.中国铁道科学，2009，30（5）：39-45.

［4］陈代海，郭文华.大跨度钢桁架拱桥的空间地震响应分析［J］.中南大学学报（自然科学版），2010，41（4）： 1590-1596.

［5］张永亮，董阳，朱尚清，等.大跨上承式铁路钢桁拱桥减震性能研究［J］.铁道工程学报， 2016，33（1）：75-79.

［6］张永亮，王云，陈兴冲，等.多维激励下大跨上承式铁路钢桁拱桥空间地震响应［J］.中国铁道科学，2020，41（5）： 56-63.

［7］陈兴冲，夏修身.大跨度拱桥地震动输入模式研究［J］.世界地震工程，2018，34（2）：26-32.

［8］杨华平，钱永久，邵长江，等.行波效应对大跨度上承式钢桁拱桥地震响应的影响［J］.铁道建筑，2014（2）：8-10.

［9］施洲，张晓珂，杨仕力，等.大跨度铁路钢桁梁柔性拱桥极限承载能力研究［J］.铁道工程学报，2018，35（5）： 30-35.

［10］施洲，张勇，张育智，等.大跨度铁路下承式钢桁梁柔性拱桥稳定性研究［J］.中国铁道科学，2019，40（4）：52-58.

［11］周超舟，赵剑发.大跨度钢桁梁柔性拱拱肋施工方案研究［J］.世界桥梁，2018，46（6）：11-15.