环保投入赋能共同富裕的理论与实证分析
2023-06-28郭晖胡伟帮张圆圆
郭晖, 胡伟帮, 张圆圆
(新疆农业大学经济管理学院,新疆 乌鲁木齐 830052)
生态环境变化与贫富差距给中国可持续发展带来了严峻挑战。“十四五”规划提出,推动减污降碳协同增效、促进经济社会发展全面绿色转型;积极扩大中等收入群体,实现共同富裕。2022年5月11日国务院常务会议,李克强总理指出,要以就业优先为导向,稳住经济大盘,扩大有效投资。环保投入包括生态治理、环保设备的研发与生产、环境公共事务发展等方面,进而可以扩大有效投资,稳岗位稳就业,增加中低收入群体收入,提高中等收入群体比重,促进共同富裕。因此,研究环保投入赋能共同富裕问题具有重大现实意义。
诸多学者利用环境库兹涅茨曲线对环境与经济增长的关系进行研究[1]。曲线呈现倒U形,环境质量随着经济增长呈先恶化后改善的趋势[2]。部分学者则从环境税的角度研究税率与经济增长的关系[3]。政府加强对环境污染的监管,而企业往往会采取对策,维护自身的经济利益[4],通过裁员来降低成本,或加强技术创新[5],寻求新的利润增长点。近年来,中国采取多种财政金融措施,消除农村贫困[6]。而贫困的消除离不开经济增长,只有不断创新,发展新兴产业,才能促进经济可持续增长,赋能共同富裕[7-8]。或者通过公共服务的均等化来降低收入不平等,提高居民的获得感,实现共同富裕[9-12]。同样,增加环保投入,减少污染,改善环境质量,并提升人类健康水平,减少贫困[13]。还有学者从制度与其他路径进行了研究和阐述,如何扩大中等收入群体,形成橄榄型分配格局,实现共同富裕[14-15]。
随着经济增长,环境会受到不同程度的影响。当经济增长达到一定程度,居民的收入水平提高,环境水平的效用随之提高,政府与企业会增加环保投入,促进重工业结构调整,并降低环境污染,改善环境质量,打破“污染-人口-贫困”(PPP)恶性循环,促进农民增收,扩大中等收入群体,推动共同富裕。
综上所述,前人主要从生态环境与经济增长的关系,或从公共服务均等化、制度等方面对共同富裕的影响进行研究。本研究将从理论与实证两个层面研究环保投入与共同富裕的关系,填补了相关研究领域的空白。可能的边际贡献:第一,研究视角与内容具有新颖性。第二,从农村与城市的角度出发,建立两部门经济模型研究环保投入与城乡收入差距之间的关系。第三,构建多元非线性回归方程,实证分析环保投入对共同富裕的影响。
1 理论研究
新凯恩斯主义理论主张,政府干预政策可以增进社会福利。以此为基础的动态随机一般均衡模型认为,每个市场参与者根据自身偏好与对未来的预期,作出跨期最优决策,并通过冲击反应函数,了解不同外生因素的冲击对经济系统的影响。比如,企业通过利润最大化作出最优决策。
假设一国分城市与农村地区,则本研究构建两部门(中间部门与最终部门)经济模型来研究环保投入对共同富裕的影响。两部门的设立,主要因为中间部门的生产提供中间产品,用于最终部门的生产,政府对最终产品征税形成税收收入,进而可增加环保投入。
1.1 企业部门
采用城乡生产函数[16],分析企业部门的经济行为,生产技术存在二元壁垒。为了简化研究,暂不考虑人口迁移。中间部门包括农村生产部门与城镇生产部门,最终部门等于农村与城镇总产出之和。
1.1.1 农村生产部门 农村生产接近完全竞争市场,劳动力主要从事农业生产。假定不存在劳动力规模效应,则农村生产函数为:
(1)
式中:Yt,n是t时期的农村总产出;At,n是t时期的技术水平;Lt,n是t时期的劳动存量;Kt,n,是t时期的资本水平。α>0,β>0,分别为劳动与资本的产出份额。假定,α+β≤1,即不存在人口规模效应。同时,假定资本折旧率为1与农产品价格Pt,n标准化为1[17]。
中国取消了农业税,则农村生产部门的利润函数为:
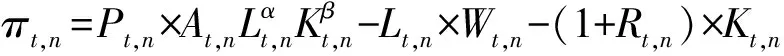
(2)
对式(2)的Lt,n和Kt,n求导得:
(3)
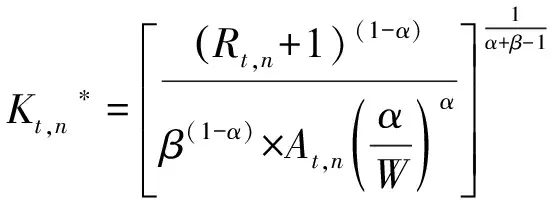
(4)
(5)
(6)
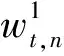
1.1.2 城镇生产部门 假定城镇的生产具有劳动力规模效应,而资本不具有规模效应。则城镇生产函数为:
(7)
式中:Yt,c是t时期的城镇总产出;At,c是t时期的技术水平;Lt,c是t时期的劳动存量;Kt,c是t时期的资本水平。γ、ε、μ>0,分别为劳动规模效应、劳动与资本的产出份额。假定,γ+ε>1,存在人口规模效应。
假定向城镇生产部门生产的产品征收θ单位税,资本折旧率为1与工业产品价格为Pt,c。则利润函数为:
(1+Rt,c)×Kt,c
(8)
对式(8)的Lt,c和Kt,c求导得:
(9)
(10)
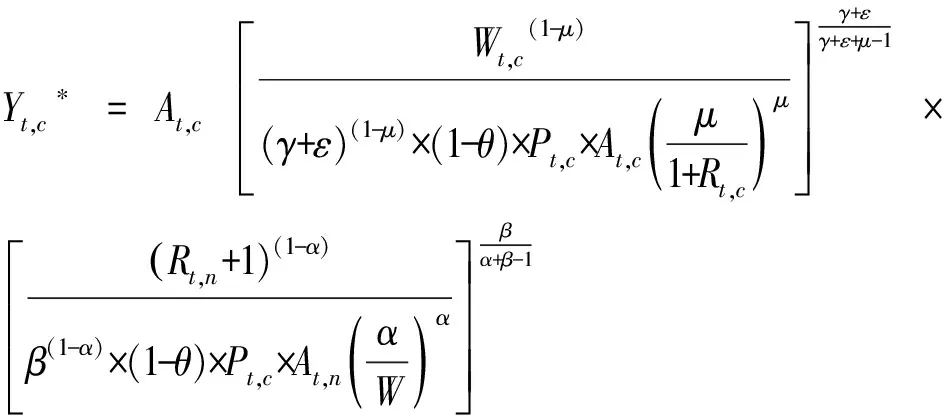
(11)
(12)
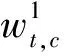
最终部门的最优生产函数为:
Yt*=Yt,n*+Yt,c*
(13)
环境恶化具有负外部性,环保投入就成为政府的重要职责。假定政府的税收只来源产量税,暂不考虑其他税收,来源税收一部分用于居民转移支付(Tt,i),另一部分用于环保投入(Xt,i)。由于不征收农业税,则:
θYt,c=Tt,i+Xt,i
(14)
1.2 均衡分析
将式(14)代入式(13)得:
(15)
由式(15)知,环保投入与经济增长呈正比,即环保投入越多,经济增长越快。
环保投入受益群体主要是城市中低收入者与农村居民。假定环保投入与中低收入群体的收入成正比,而中低收入群体的收入与基尼系数成反比。则:
yt,i=yt,i(Xt,i,Zt,i)
(16)
ginit,i=ginit,i(yt,i,wt,i)
(17)
式中:yi,t代表中低收入群体收入;Xt,i代表环保投入;Zt,i代表影响其收入的其他因素;ginii,t代表贫富差距;wt,i代表影响贫富差距的其他因素。贫富差距与中低收入群体的收入成反比,由式(16)与式(17)解出:
Xt,i=yt,i(Xt,i,Zt,i)-1
(18)
yt,i=ginit,i(yt,i,wt,i)-1
(19)
由式(18)与式(19)得:
Xt,i=[ginit,i(yt,i,wt,i)-1]-1
(20)
所以,环保投入与贫富差距成反比。即增加环保投入,提高中低收入群体的收入,降低基尼系数,缩小贫富差距。
综合式(15)与式(20)可知,增加环保投入,促进经济增长,带动中低收入群体就业,增加其收入,缩小贫富差距,推动共同富裕。
2 实证分析
2.1 计量模型的构建
参考前人研究环保问题的模型[14],通过豪斯曼检验结果得出,选择固定效应模型比随机效应模型效果更好。所以,采用个体时点双固定效应模型,建立非线性计量模型[18],设计如下:
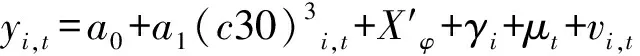
(21)
(22)
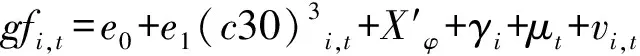
(23)
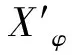
2.2 指标选取及数据来源
2.2.1 指标选取 被解释变量—基尼系数(ginii,t)。表示贫富差距,基尼系数根据洛伦茨曲线计算出来,越接近于0,表明收入分配越平等;越接近于1,表示收入分配越不平等。yi,t是t时期的人均国内生产总值。人均国内生产总值越大,该国居民越富裕。共同富裕(gfi,t)的定义[19]:
gfi,t=yi,t×exp(-ginii,t)
(24)
核心解释变量—环保投入(c30i,t)。采用工业治污完成投资来表示,主要考虑工业污染对人类健康的影响相对大,容易引发疾病风险,进而增加贫困的发生率,同时也考虑到数据的可获得性。加大工业治污投入,发展绿色经济,可以促进经济转型升级,同时扩大中低收入群体就业,促进其收入增加,缩小贫富差距,实现共同富裕。
控制解释变量。工业经济发展,带动中低收入群体就业;对外开放,促进经济发展;技术进步,促进产业结构高级化;高等教育,根据内生增长理论,提高人力资本,促进经济长期发展;互联网设施建设、电商发展,促进产业结构转型升级,助力经济可持续发展。
2.2.2 数据来源 采用省域面板数据,数据来源于2009—2020年的《中国统计年鉴》《中国人口与就业统计年鉴》。通过计算整理得到经济增长、贫富差距、共同富裕、工业经济发展、对外开放、技术进步、高等教育、互联网设施、电商发展等变量的数据。由于2021年部分数据缺失,暂时未考虑纳入。变量含义及描述性统计见表1。

表1 变量含义及描述性统计
2.3 计算结果与分析
2.3.1 经济增长、贫富差距方程的回归分析结果 基于稳健标准误回归结果如表2所示。由列(1)看出,在没有加入控制变量的情况下,环保投入的立方项的估计系数为0.134,通过显著性水平10%的统计检验。由列(2)看出,在加入控制变量的情况下,环保投入的立方项的估计系数为0.348,通过显著性水平5%的统计检验,所以,环保投入的立方项对经济增长具有正向的显著性影响。同理,由列(3)和列(4)看出,环保投入的立方项对贫富差距具有负向的显著性影响。因此,上述的理论研究结果得证。
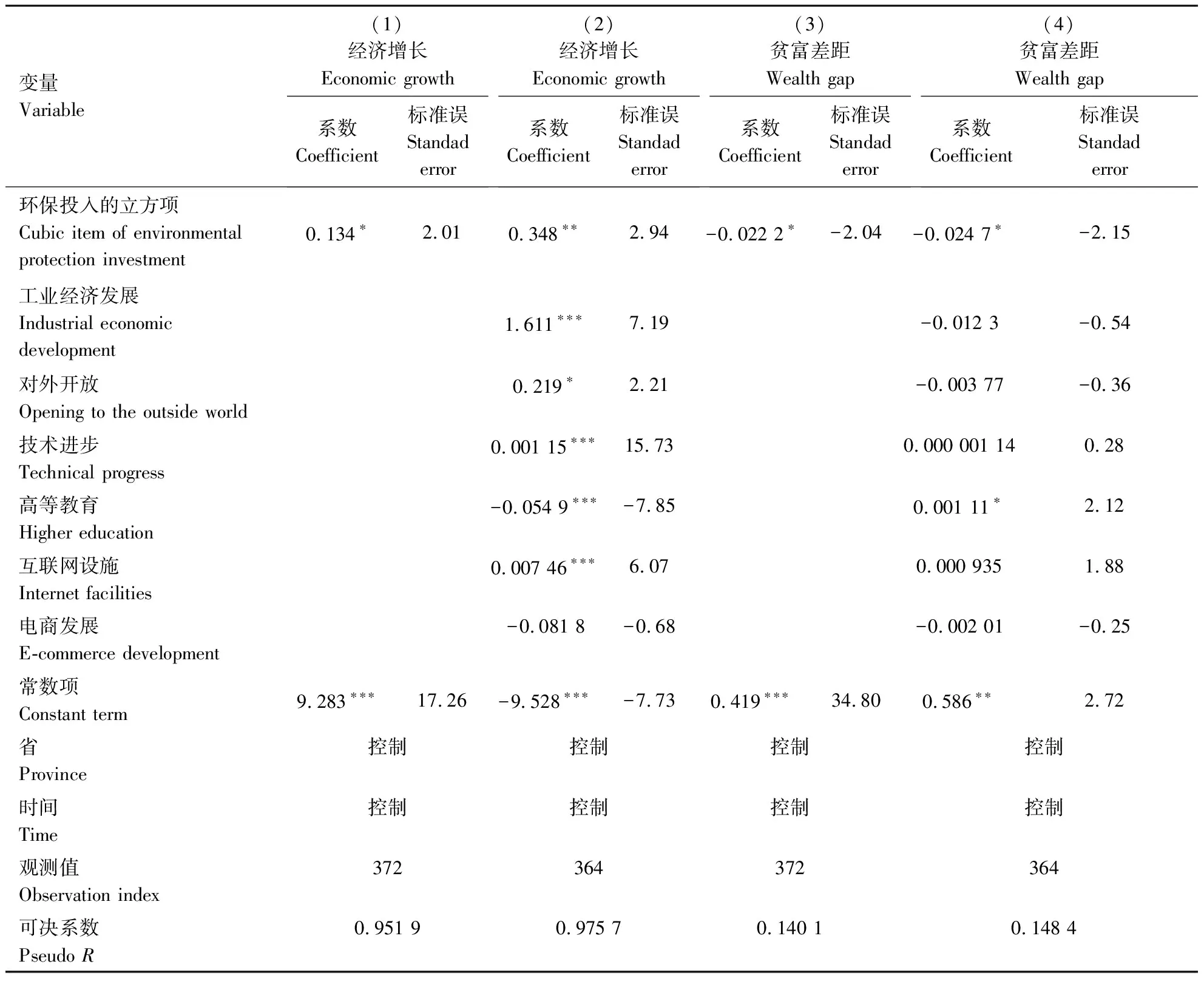
表2 经济增长及贫富差距基准模型回归结果
2.3.2 共同富裕方程的回归分析结果 由表3可知,由列(1)和列(2)可以看出,在没有加入控制变量时,环保投入的立方项的估计系数为0.197,通过显著性水平10%的统计检验。在加入控制变量时,环保投入的立方项的估计系数为0.351,通过显著性水平5%的统计检验。所以,环保投入的立方项对共同富裕具有正向的显著性影响。

表3 共同富裕基准模型回归结果
2.3.3 稳健性回归分析结果 变换被解释变量的设置。参考前人研究的方法[20],将基尼系数换成其他方法构造的基尼系数,gf2代表基尼系数的前2期的平均值构造的共同富裕指数;gf3代表基尼系数的前3期的平均值构造的共同富裕指数;gf4代表前4期的基尼系数构造的共同富裕指数。回归分析结果如表4所示,由列(1)知,环保投入的立方项的估计系数为0.261,通过显著性水平5%的统计检验。由列(2)知,治污投入的立方项的估计系数为0.306,即在显著性水平1%下,环保投入显著地促进共同富裕。由列(3)知,环保投入的立方项的估计系数为0.300,通过显著性水平5%的统计检验。
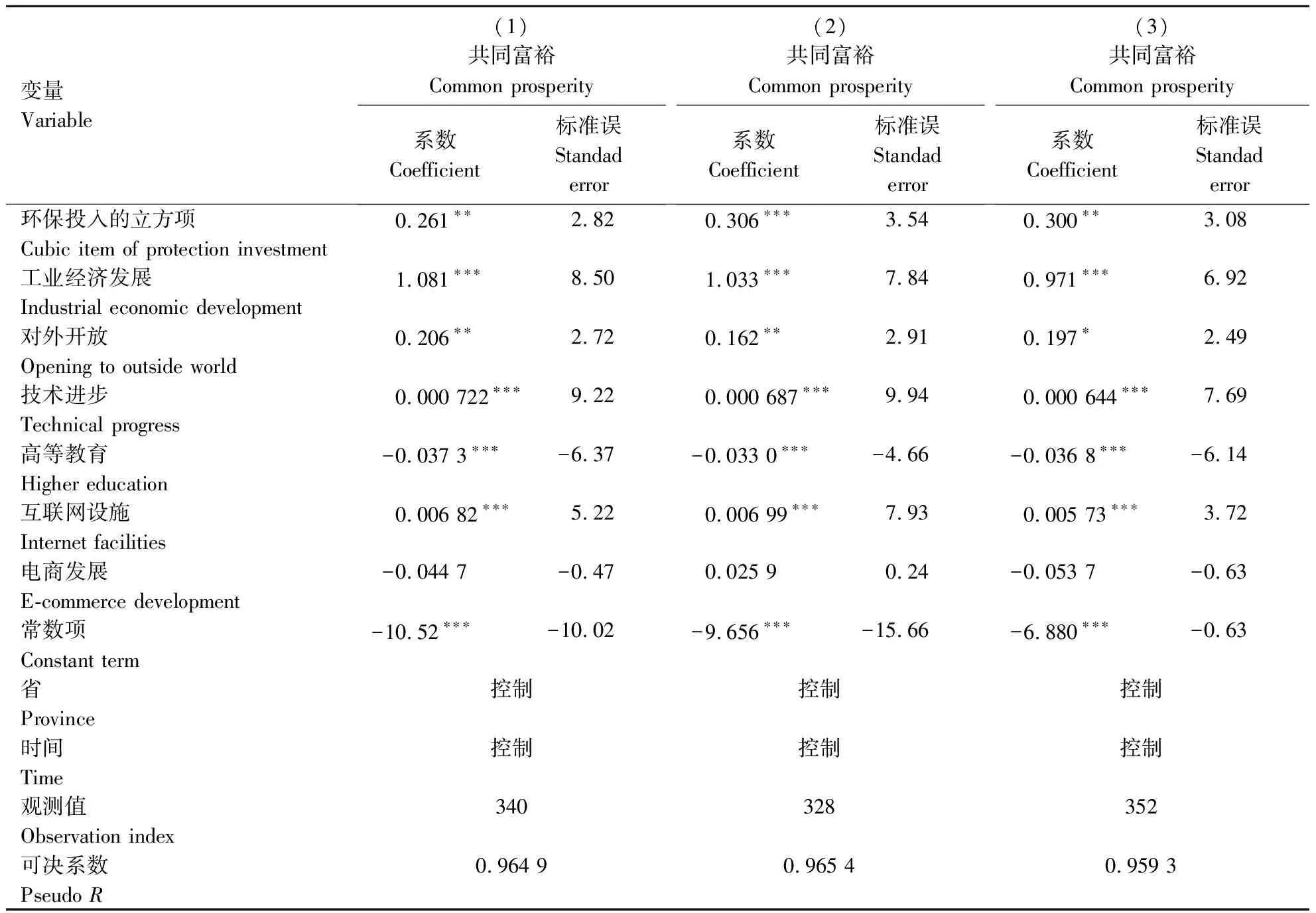
表4 共同富裕基准模型的稳健性分析结果(1)
替换核心解释变量。第一,将工业污染治理投资替换成工业治理废气投资,回归分析结果如表5所示。由列(1)知,工业治理废气投资的影响系数为3.20e-19,通过显著性水平10%的统计检验。第二,将工业污染治理投资替换成绿色信贷指数,由列(2)知,绿色信贷指数的立方项的估计系数为7.12e-13,即在显著性水平1%下,绿色信贷指数的立方项显著地促进共同富裕。综上,环保投入对共同富裕的影响具有稳健性。
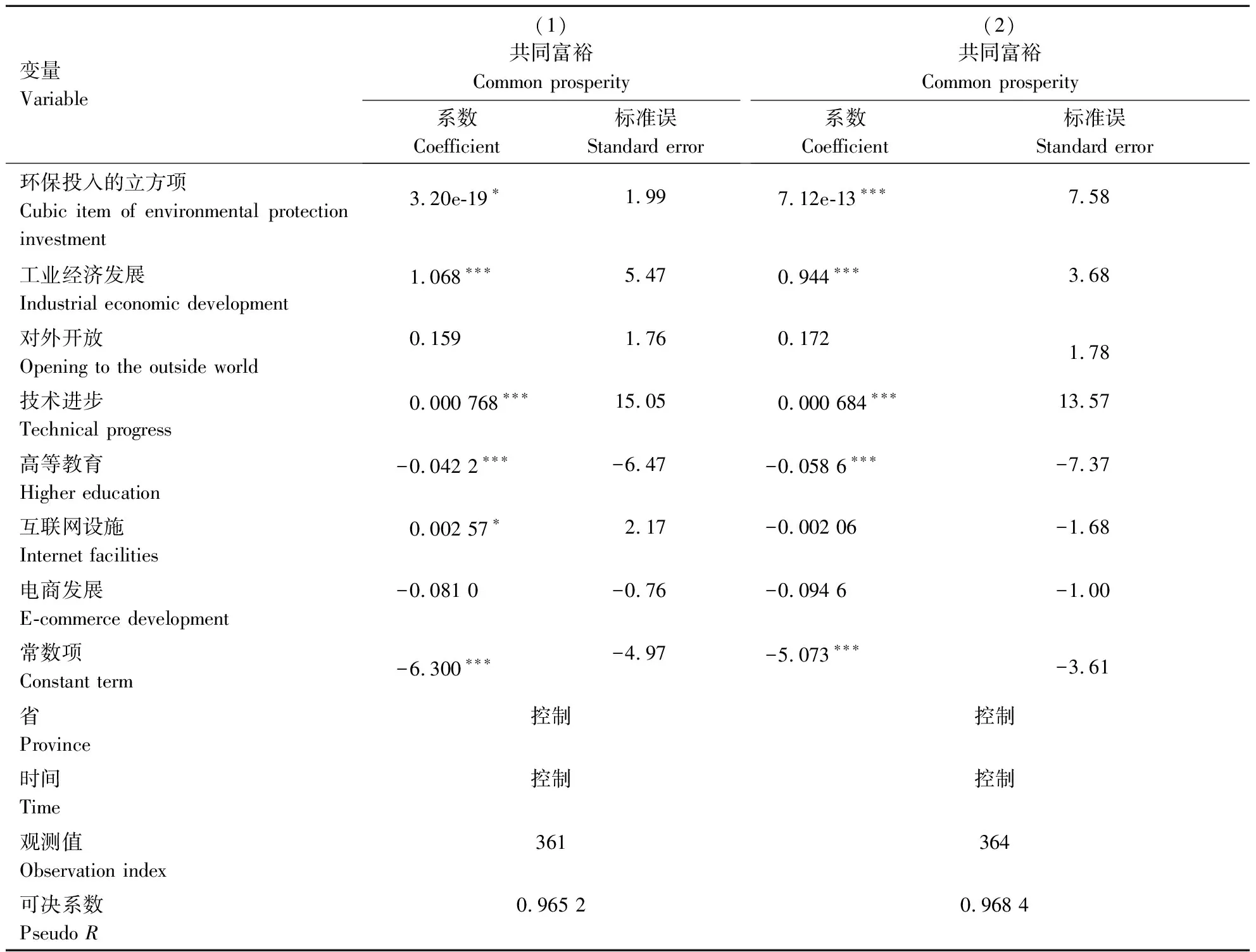
表5 共同富裕基准模型的稳健性分析结果(2)
2.3.4 共同富裕的差分GMM模型回归分析结果 由于绝大多数实证研究都基于非实验性数据,且很多变量无法观察到,则存在测量误差与模型设定误差,会造成内生性问题。将滞后水平作为一阶差分的工具变量,而一阶差分又作为水平变量的工具变量,而且任何经济因素都可能存在惯性与滞后效应。表6给出了动态面板广义矩估计的结果,采用两步法分析得出结果如列(1)知,环保投入的立方项的影响系数为1.268,通过显著性水平10%的统计检验。而一阶扰动项存在自相关,二阶扰动项不存在自相关,表明原模型的随机扰动项不存在自相关。同时,Sargan检验P值不显著,说明该模型的工具变量选取合理而且有效。同理,从列(2)知,环保投入的立方项的影响系数显著为1.300,也通过了相关检验。
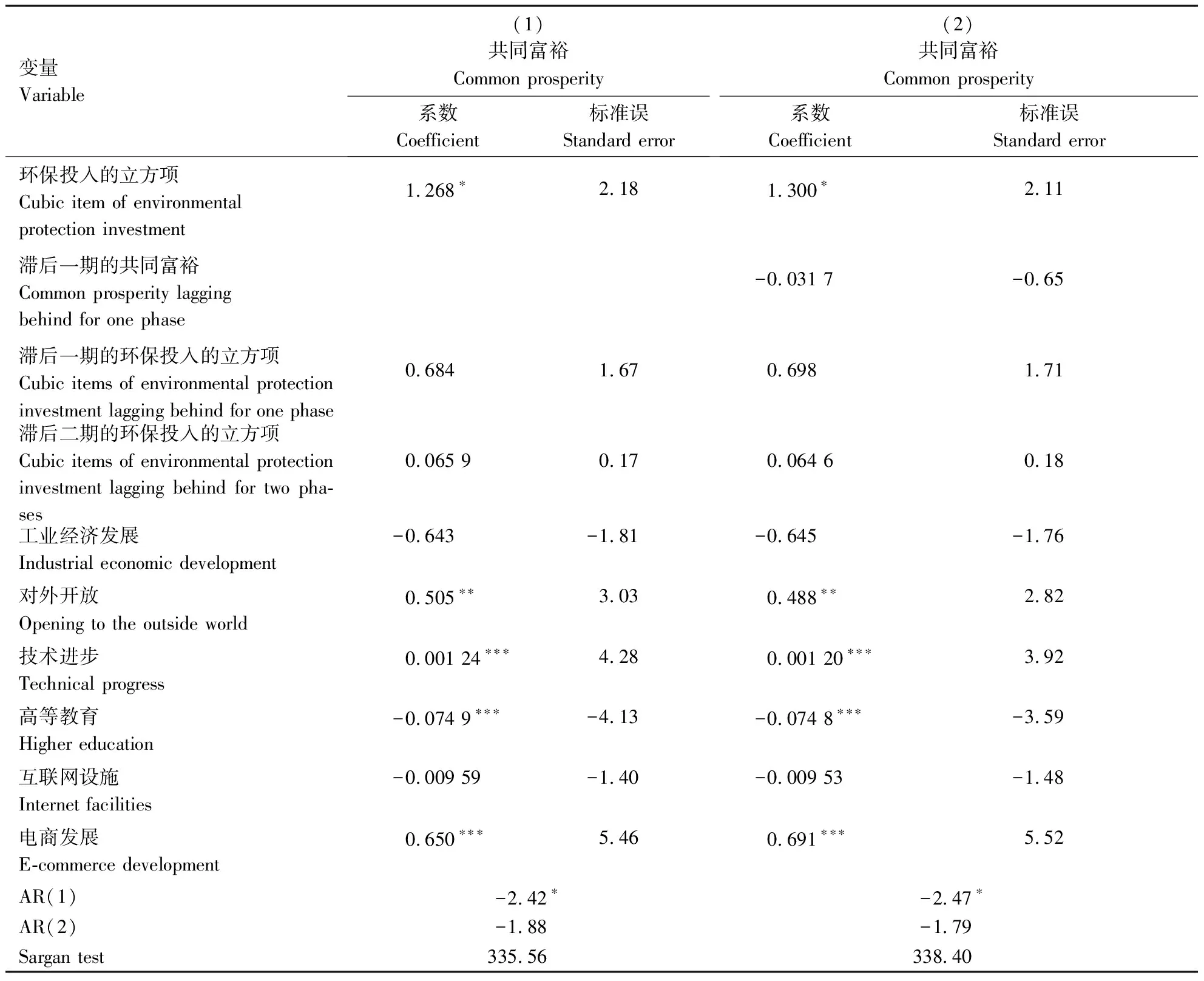
表6 基于GMM的回归分析结果
通过与表3的基准回归做比较,环保投入的立方项的估计系数为0.351,相对GMM的回归分析结果得出的估计系数低估,而表6的列(2)比列(1)的估计系数相对高,这是因为共同富裕的一阶滞后项的系数为负,即上一期对当期的共同富裕具有抑制作用,比如,上一期经济形势向好时,当期可能会收缩财政货币政策,这也一定程度上解释了上一期对当期的共同富裕产生负效应。
3 结论
本研究理论与实证相结合,分析了环保投入对共同富裕的影响。研究结果表明,增加环保投入,促进经济增长,缩小贫富差距,实现共同富裕;环保投入对共同富裕具有显著性的非线性的正向影响,而且该影响具有稳健性。通过差分GMM模型分析其内生性,表明OLS回归结果低估了环保投入对共同富裕的影响。因此,以上结论为中国环境保护与共同富裕政策的制定提供了思路。第一,加大政府支持环保投入力度,运用多种政策工具拓宽投资渠道;第二,促进工业治污投资,鼓励采用绿色技术,积极开发利用清洁能源;第三,提升绿色金融的支持,引导企业对绿色经济的投资。在此基础上,稳岗位稳就业,拓展中低收入群体居民收入增长渠道,扩大中等收入群体,促进共同富裕。
