基于量子遗传算法的火力分配

李 闪，王新宇，麻志强，卫景宠，田 杰

（北方自动控制技术研究所，太原 030006）

0 引言

多目标防空中的火力分配问题是防空作战中的研究重点［1］。现今防空作战的整体环境正朝着联合防空的方向发展，在进行防空火力分配时应充分考虑多平台、多火力单元之间相互协同的特点，针对来袭目标的武器数量、威胁度以及武器特点，完成多点对多点的火力分配任务。因此，火力分配是一个离散且具有一定约束条件的规划求解问题，此类问题属于典型的NP（非确定多项式）问题［2］，此类问题的求解难点在于当防空武器和来袭目标数量增加时，其解空间会以指数形式增长。

当前普遍使用的遗传算法在应对这种复杂优化问题时经常因选择、交叉、变异参数选择不当，而出现难以收敛和局部极值、求解结果差异性大等问题。文献［3］对遗传算法的收敛速度进行了优化，但是未能解决结果稳定性的问题，解算的最优值有所下降。文献［4］将模拟退火算法与遗传算法结合具有较好的全局搜索能力，但是耗时较长。文献［5］使用的NSGA-II 算法在低维多目标优化问题中具有优势，但不适用高维多目标问题。文献［6］提出的NLPCGA 算法对遗传算法作出了优化，但是未能从根本上解决对参数选择的依赖问题。量子遗传算法（quantum genetic algorithm，QGA）就是将量子态与遗传编码相结合［7］，用量子门代替遗传算法中选择、交叉、变异的更新方法，实现种群基因的进化，从而达到优化求解的目的。量子遗传算法在解决此类问题时，可以只依赖目标函数的适应度值在概率引导下进行全局自适应搜索［8］，并不局限于问题的特性、优化形式等因素，具有可靠的稳定性。量子态是量子计算中的基本信息单元，量子计算利用量子态的叠加、纠缠等性质，可以实现许多难以处理的经典NP 问题，这种方法可以取得很好的优化结果，可以摆脱分配求解时算法参数的选择依赖问题。

本文在建立火力资源及约束的基础上，以毁伤效益为评价标准建立了火力分配模型，并利用量子遗传算法对模型求解，通过仿真实验对量子遗传算法在此类问题上的可行性进行分析，并与遗传算法仿真结果相比较，体现了该算法在解决此类问题上的可行性和有效性。

1 火力分配模型

1.1 火力分配流程

火力分配是防空作战的重要环节，现代防空作战已基本形成了远中近结合、软硬多武器平台协同作战的运用原则［9］。作战过程中防空火力分配需根据战场态势进行机动调整，并优先打击对我方保卫对象威胁度较高的目标。依据来袭目标的威胁度和防空武器系统的射击有利度，进行火力分配，流程如图1 所示。

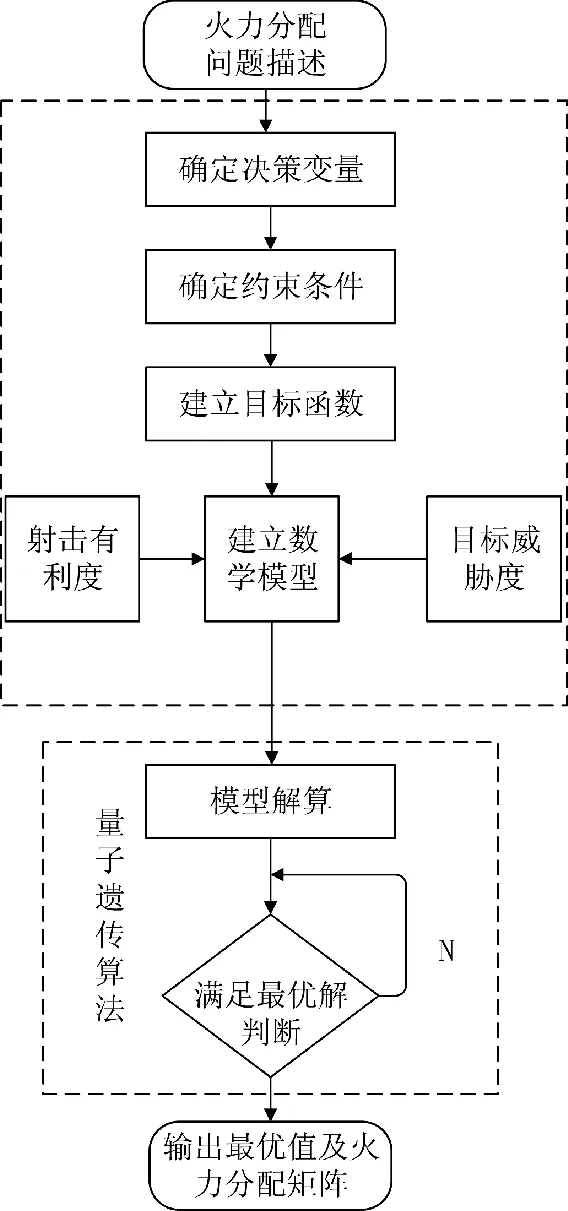
图1 火力分配流程Fig.1 Flow chart of firepower distribution

1.2 模型假设

假定在某次防空作战中，我方共有多组防空武器参与拦截，防空武器系统分解后，共有u 个可控火力单元，拦截预警系统发现的n 批空中来袭目标，每批次包含多个可拦截目标，数量为v。我方防空武器集合D={d1，d2，…，du}，空中目标集合T={t1，t2，…，tv}。空中目标对我方保卫目标的威胁度为W={w1，w2，…，wv}，其中可认为同批次内的同类型目标威胁度相同。

1.3 模型建立

在对防空火力单元进行分配前应考虑火力单元的约束条件，建立其对空中目标的约束向量Ri={ri1，ri2，…，riv}，Ri（i=1，2，…，u）表示防空武器第i 个火力单元对每个空中目标的约束向量，火力单元对空中目标的约束矩阵R：

Ri中元素均为0 或1 的二值变量，取值考虑该火力单元对某个空中目标的状态约束，可以分配为1，不可分配为0，如资源约束（已消耗为0，未消耗为1）、转火时间（火力单元的转火时间在分配环节时间要求取值1，不满足取值0）、故障约束（火力单元状态正常取值为1，故障状态取值0）。

约束矩阵R 表征了火力单元对空中目标的分配是否有效，只有满足所有约束时，火力分配的结果才有意义。在火力分配前可根据武器单元状态灵活调整约束矩阵。

针对来袭目标，作出火力分配，火力分配决策矩阵Xf为：

期望获得目标毁伤的收益最大，目标毁伤函数如式（1）所示。

式（1）中，qij为第i 个防空火力单元对第j 个空中来袭目标的射击有利度。

为实现最大限度拦截来袭目标，需要确定模型的约束条件。多组防空武器系统分解为最小火力单元之后，每个火力单元只能分配一个目标，在决策矩阵中体现为：

其取值由约束矩阵确定，如式（3）。若当前某个火力单元对所有目标均不满足射击条件，则退出此次分配。

面对空中来袭目标时需保证我方最少有一个防空火力单元被分配用于拦截该目标的袭击，在决策矩阵中体现为：

在实际情况中，应根据当前时刻火力单元对空中目标的状态，随时调整约束矩阵R。这样可以在火力分配的同时充分考虑单个火力单元的状态。

综上所述：

可以看出多目标火力分配是一个有条件约束的非线性混合整数多解寻优问题，相比一般的非线性多解寻优问题，对解算算法有着更高的要求。

2 量子遗传算法的实现

运用量子遗传算法对防空火力规划进行求解，与遗传算法的解算流程不同，量子遗传算法在个体的编码方式上采用量子比特编码，在种群的进化上利用量子门更新种群。

2.1 量子比特编码

在量子遗传算法中，引入量子比特来完成基因的存储和表达。量子比特是量子信息中的概念，它与经典比特不同，是因为它可以在同一时刻处于两个状态的叠加中［10］。一个两态的基因使用一个量子比特编码则有：

α 与β 是概率幅常数且取值满足式（7）。

φ 不再表达一个确定的信息，可以为“0”态也可以为“1”态，成为一个拥有表达二者可能的信息。

对多目标的火力分配这一数学模型，则需要引入多量子比特的编码。因为空中目标具有多批次、多数量的特点，每个防空火力单元的打击决策也具有多种可能。使用n 个量子比特编码对种群中1 个个体的m 个参数的基因进行编码：

使用量子比特编码的染色体可认为是多个状态的叠加，具有表达所有基因的可能性，对该基因的任意一个操作会影响到其所表示的所有可能信息，因此，与经典遗传算法相比可以获得更好的多样性特征。随着种群的不断演化，|α|2或|β|2会趋于0或1，最终收敛到一个确定状态。

2.2 量子旋转门更新

2.2.1 量子旋转门

量子门是算法中实现演化的重要步骤。量子门的选择直接决定了种群能否演化成功和演化的方向［11］。根据火力分配的计算特点，这里选择量子旋转门作为种群的进化策略。θi为旋转角，则量子旋转门的调整操作为：

更新方法：

［αiβi］T是第i 个量子比特在经过量子旋转门操作前的概率幅常数，其经过更新后：

2.2.2 更新方法

先调整策略，确定旋转角θi，在对当前个体u 进行更新时需要对比当前种群中最优个体best 确定旋转角方向s（αi，βi）。计算当前个体测量值的适应度f（u）与当前种群中最优个体的适应度f（best）。如果f（u）＞f（best）则改变u 中的对应的量子比特，引导概率幅常数αi，βi向着有利于个体u 产生的方向进化，如果f（u）＜f（best）同样改变u 中对应的量子比特，引导概率幅常数αi，βi向着有利于个体best 产生的方向进化。

2.3 量子遗传算法的实现流程

量子遗传算法计算步骤：

1）将防空火力单元对空中目标的火力决策矩阵作为种群个体，随机生成以多个量子比特为编码的染色体，并对染色体中的全部基因进行初始化，种群中个体的全部基因（αi，βi）均初始化为（，），同时按照种群大小生成初始化种群Q（t0）。这样生成的初始种群的基因表达每个可能状态的概率都是相等的。

2）利用测量函数对初始种群的所有个体进行一次测量，得出一组解，它不是火力分配的决策矩阵而是一个长度为n 的二进制编码P={p1，p1，…，pn}，其中，pj是该代种群中的第j 个个体的测量值。然后进行适应度评估并找出最佳适应度个体，以此作为下一代种群的进化方向。

3）算法开始循环迭代，在迭代中，每次都需要对种群进行测量以得出一组解P（t）并计算相应的适应度值，利用量子旋转门和旋转角方向调整进化方向，使种群的解不断向最优解收敛。

算法实现流程如图2 所示。

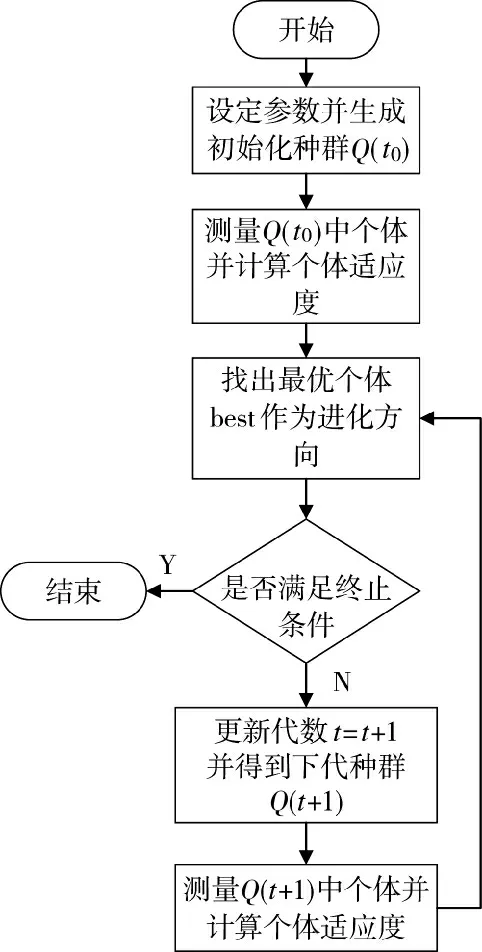
图2 量子遗传算法实现流程Fig.2 Implementation flow chart of quantum genetic algorithm

3 仿真结果及分析

假设我方侦察预警系统某次侦测到敌方有3批次空中目标，每批次包含2 个同类型空中武器。我方在来袭方向的防御地带上部署的防空武器系统经分解后有10 个火力打击单元。空袭武器对我方保卫目标的威胁度为：

各火力单元对空中目标的射击有利度为：

利用量子遗传算法进行火力分配，参数设置种群规模为40，进化迭代次数为200。当前个体基因的旋转角和旋转方向由其与最优个体适应度值的大小确定，量子旋转门的旋转角θi=Δθi·s（αi，βi），旋转角度Δθi与方向s（αi，βi）的调整策略使用文献［12］所提出的通用调整策略，如表1 所示。

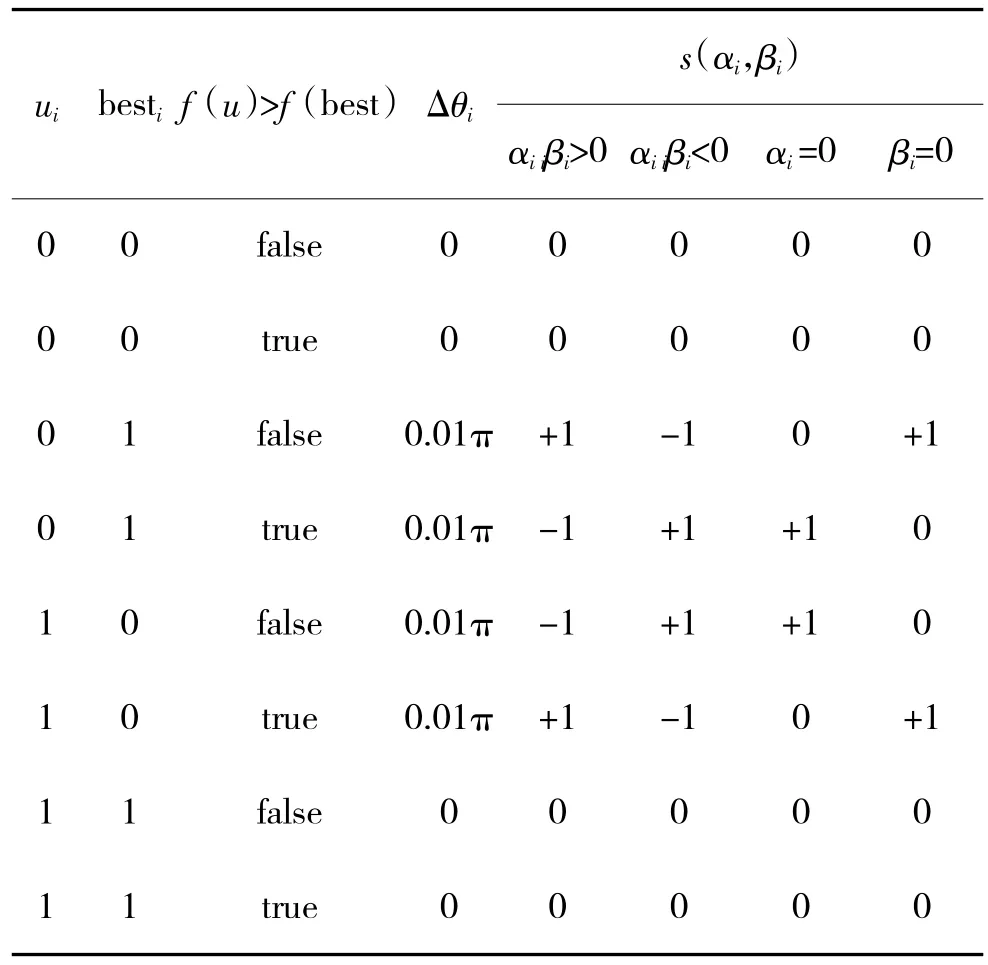
表1 旋转角调整策略Table 1 Adjustment strategy of rotation angle

使用式（5）所提出模型，以最大毁伤收益为目标，火力单元对空中目标的约束矩阵取R，得到火力决策矩阵X：

由决策矩阵，此次火力分配结果如表2 所示。

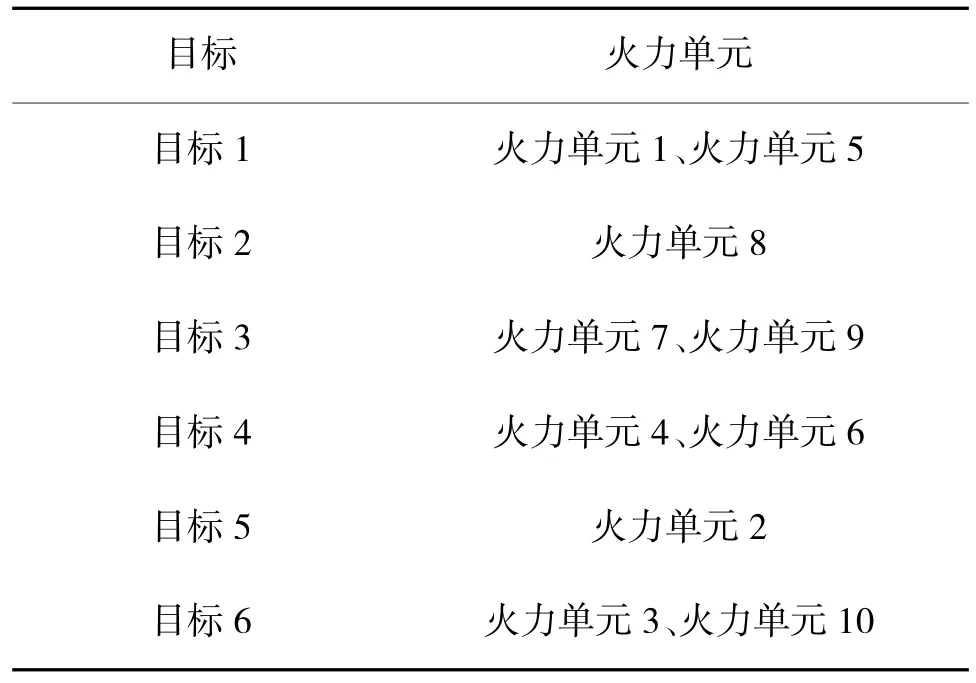
表2 火力分配结果Table 2 Fire distribution results

最大毁伤收益（最优适应度值）FQ=2.783 2，最优适应度值的收敛曲线如图3 所示，即使陷入局部最优之后，经过一定次数迭代仍然可以跳出局部最优。

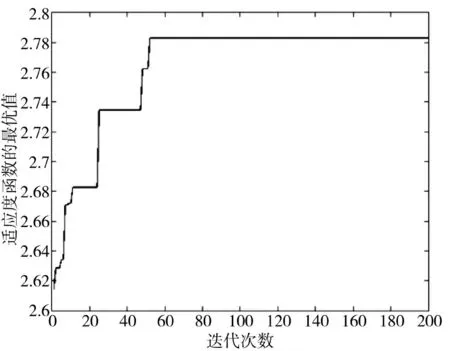
图3 最优适应度值的收敛曲线Fig.3 Comparison of optimal values of two kinds of algorithms

使用量子遗传算法和遗传算法分别求解50次，遗传算法变异概率设置为0.1，其余参数均设置迭代次数100、种群规模50。计算最优适应度值的均值、极差和标准差，比较两种算法的适用性和稳定性，比较结果如表3 所示。

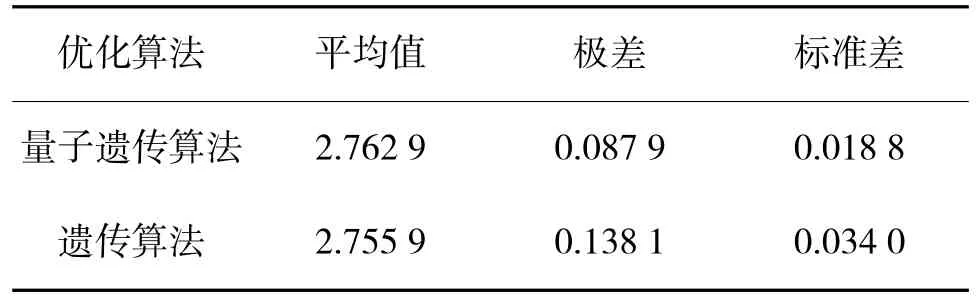
表3 两种算法最优值比较Table 3 Comparison of optimal values of two kinds of algorithms

由量子遗传算法的火力分配结果可以看出，量子遗传算法适用于解决多目标防空的火力分配问题，并且与遗传算法相比最优适应度的均值有所提升，同时保持极差和标准差较小。量子遗传算法的分配结果与遗传算法相比，在保持毁伤收益增加的同时还可以取得更好的稳定性，避免某次分配结果极差的情况出现，体现了该算法的适用性、优越性和稳定性。

4 结论

针对空中目标进行火力分配时，将各平台防空武器系统分解为可规划的最小火力单元，利用火力单元对空中目标的状态约束矩阵加以限制，可以兼顾多武器系统的武器特点和使用情况，并且以最大毁伤收益为目标函数，建立了多目标的火力分配模型，针对遗传算法的不足引入量子遗传算法对模型进行解算。为解决多武器平台联合防空作战中对空中目标的火力分配问题提供了一种新的解决办法。仿真结果表明，量子遗传算法适用于火力分配模型的解算，并且与遗传算法相比，在毁伤收益上有一定程度的提升，在算法的稳定性上也有较大幅度的改善，可以解决求解时算法参数的选择依赖问题。