基于控制器动态线性化的数据驱动ILC*

徐通福，李秀英

（上海应用技术大学，上海 201418）

0 引言

迭代学习控制（iterative learning control，ILC）利用有限时间内先前迭代的信息来提高重复操作系统的跟踪性能［1］。它已经广泛应用于机器人、划片机、红外相机和列车等重复系统［2-5］。对于大多数现有的迭代学习控制方法，控制器的设计和稳定性的分析需要知道被控对象的动态模型。从这个角度来看，它们被认为是基于模型的ILC。基于模型的ILC是使用基本原理或辨识方法对被控对象建模。如果对象是复杂的，那么基于模型设计的控制律的结构也会变得复杂，这导致控制器设计耗时、低效，甚至在某些实际情况下是不可能的。

为了解决基于模型的ILC 带来的一些问题，数据驱动的控制方法近年来吸引了越来越多的关注。李佳伟等在迭代学习控制的基础上引入遗忘因子，减少了系统的超调和振荡［6］。薄雨蒙等将基函数前馈调参技术和ILC 技术结合，有效地提高了对时变的期望轨迹的控制精度［7］。梁建智等利用数据驱动迭代控制大大减小了数控机床位置跟踪误差［8］。

数据驱动的迭代学习控制方法虽然消除了基于模型的控制方案的一些问题，但是仍然存在一些关键的问题。例如：学习控制器的设计通常是根据经验或一些系统知识确定的；学习控制增益没有精确地校准，只是采用固定的学习控制增益，该增益通常在迭代过程中启发式地确定。对此，本文对一般的未知非线性重复系统，提出了一种新的数据驱动迭代学习控制方法。首先，基于非线性理想学习控制器的动态数据模型，确定带有学习控制增益向量的迭代学习律。然后，利用改进的无模型自适应迭代学习控制（improved model free adaptive iterative learning control，IMFAILC）方案对学习控制增益向量中的复杂非线性进行估计，IMFAILC 方案的引入提高了被控对象的非线性跟踪能力。

1 理想学习控制器的动态线性化

考虑未知的重复离散时间非线性非仿射单输入单输出系统

假设1：非线性系统（1）在迭代域中满足广义利普希茨条件，也就是说，对于任意时刻k 和迭代i，如果，那么有一个未知的常数b＞0 使得

备（1），理想的学习控制器可以表示为

由于理想学习控制器式（3）的结构是未知的，所以它只是一个理论表达式。在实践中，通常根据经验或使用一些系统知识来选择具有先验确定结构的迭代学习控制律。然而，当被控系统的动态是未知的，并且可能是复杂的，具有强非线性和时变参数、阶数和结构时，很难确定所设计的ILC 在实践中是否有效。因此，需要寻求一种系统的方法来设计专门针对未知受控对象的迭代学习控制律。

定理1：对于满足假设1 和假设2 的理想学习控制器式（3），如果，那么式（3）可以等价地变换为下面的动态线性化学习控制器（dynamic linearization learning controller，DLLC）［9］

应迭代学习控制［10-11］。假设3 表明控制器输出的无界变化不能由先前迭代中e（·）和u（·）的有界变化产生。许多方法，如P 型迭代学习控制和牛顿型迭代学习控制［12］，都满足这些假设。

2 学习控制系统设计

所得到的DLLC 式（5）在数学表达式上是式（3）的等价，且受控系统式（1）的非线性包含在学习控制增益向量中，因此，可以被认为是一个非线性函数。为了估计DLLC 式（5）中的可以使用估计算法，例如投影算法［13］。然而，当受控设备式（1）的物理动态具有强非线性和时变结构、顺序和参数时，这种参数估计算法可能导致较差的跟踪性能。本文为了估计，设计如下准则函数

式中，α 是权重因子，用来限制控制输入量的变化。等式右边的第1 项是基于传统的参数估计准则函数即最小化真实值与估计值之差的平方，然而，仅仅应用此类准则函数推导出的估计算法，其参数估计值会对某些不准确的采样数据过于敏感，基于此，设计了等式右边的第2 项。此外，等式右边的第2 项包含了跟踪误差，即在设计控制增益时，考虑了全局的优化性能。

式中，γ 和δ 代表步长因子，加入γ、δ 使该算法具有更强的灵活性和一般性。

为了增加估计算法式（7）对时变参数的跟踪能力，设置如下重置算法

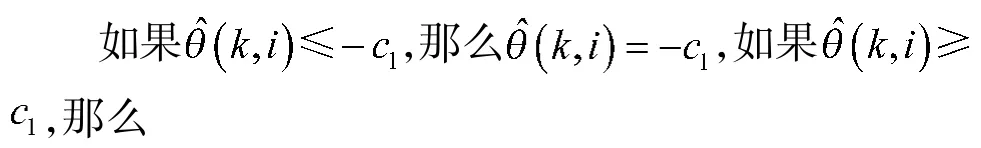
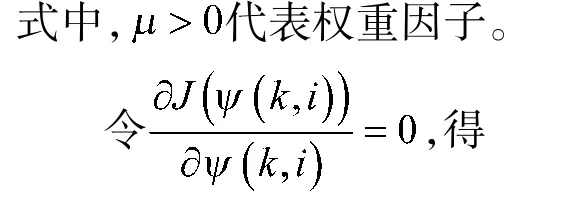
同样为了使估计算法式（9）对时变参数具有跟踪能力，设置如下重置算法

根据式（12），式（5）可重写为

式（8）、式（10）～式（13）共同组成了系统的学习控制律，本文称其为基于动态线性化学习控制器的改进的无模型自适应迭代学习控制（improved model free adaptive iterative learning control based on dynamic linearization learning controller，IMFAILC-DLLC）。

与现有的数据驱动控制方法相比，所提出的方法的主要优点在于，通过基于所建立的动态线性化数据模型优化控制目标函数，以系统的方式设计学习控制器，独立于被控对象的动态特性，并且沿着迭代轴使用动态线性化方法直接构造，而不是间接地基于对象的特定模型。另一个改进是利用IMFAILC 方案对理想学习控制器增益进行自适应逼近，提高了被控对象的跟踪性能。

3 仿真

本章给出了两个例子来证明IMFAILC-DLLC迭代学习控制的有效性。第1 个例子是在一个复杂的非线性SISO 系统上进行的，该系统具有时变的参数、阶数和结构。第2 个例子是通过一个类似于高速列车模型进行的，这是一个典型的非线性SISO 系统［9］。为了与本文提出的IMFAILC-DLLC 迭代学习控制相比，MFAILC［14］和RBF-DLLC 迭代学习控制［9］也用于这两个例子。此外，初始控制器和被控对象的输入输出数据通过无模型自适应控制来产生［15］。

3.1 数值仿真

考虑以下非线性系统［9］

式中，是时变参数。期望输出为

图1～图3 是IMFAILC-DLLC 迭代学习控制、RBF-DLLC 迭代学习控制和无模型自适应迭代学习控制在第1，20，40 和100 次迭代时的跟踪性能。第1 次迭代的跟踪误差由无模型自适应控制产生，以保证3 种迭代学习控制方法具有相同的跟踪性能。结果表明，IMFAILC-DLLC 迭代学习控制与RBF-DLLC 迭代学习控制在第20 次迭代后的大部分时间间隔内具有令人满意的跟踪性能，而无模型迭代学习控制与期望轨迹仍有较大偏差，特别是在500 时刻以前。

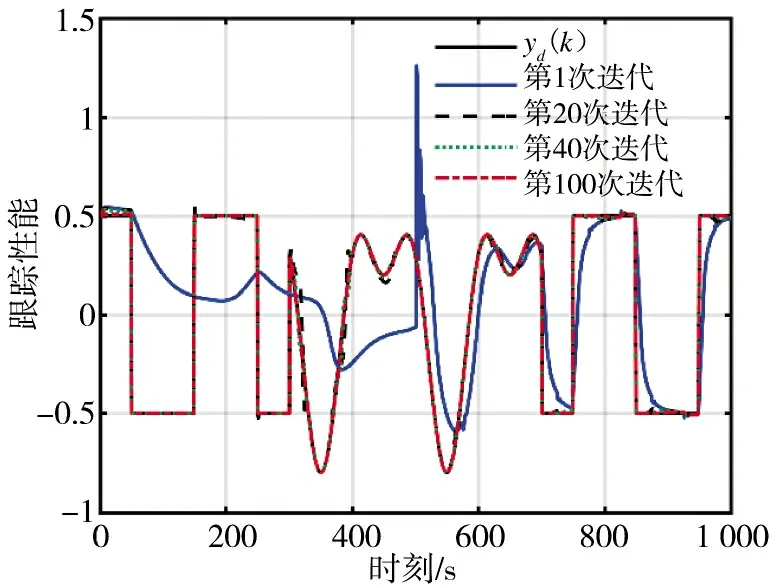
图1 IMFAILC-DLLC ILC 跟踪性能Fig.1 Tracing performance of IMFAILC-DLLCILC

图2 RBF-DLLC ILC 跟踪性能Fig.2 Tracing performance of RBF-DLLC ILC

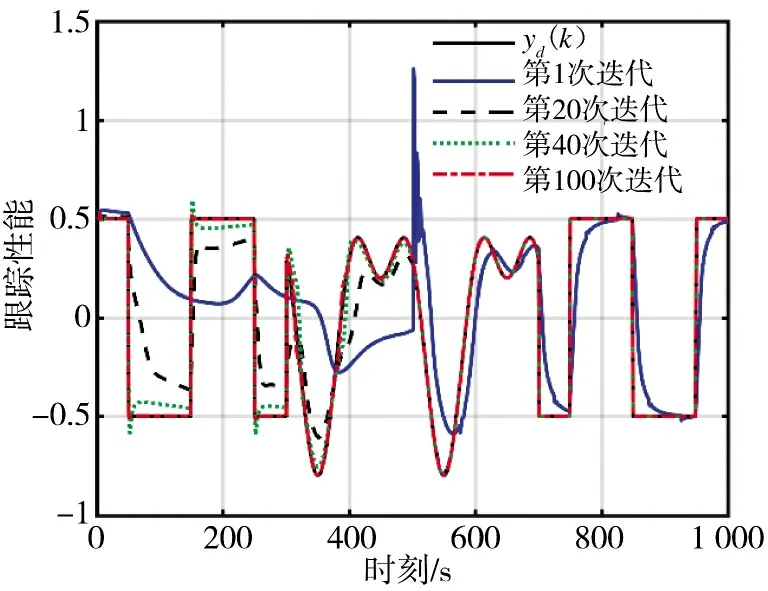
图3 MFAILC 跟踪性能Fig.3 Tracing performance of MFAILC

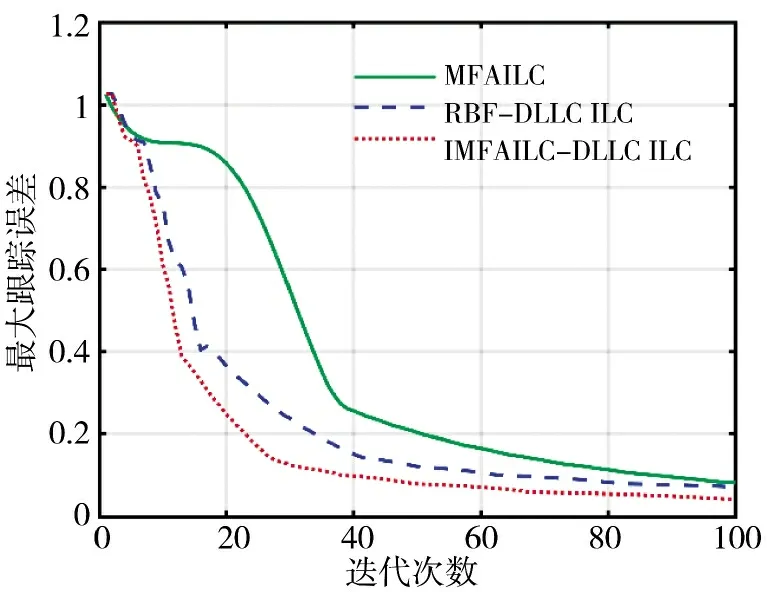
图4 迭代过程最大误差Fig.4 Maximum error of iterative process

图1～图4 的仿真结果表明，对于参数、阶数和结构随时间变化的复杂非线性SISO 系统，所提出的IMFAILC-DLLC 迭代学习控制优于RBF-DLLC迭代学习控制和无模型自适应迭代学习控制。

3.2 高速列车模型仿真

高速列车的动态离散时间模型如下所示［9］

其中，系统输出v（k）（m/s）是高速列车的速度，控制输入F（k）（N/kg）是单位质量上的牵引/制动力，ts=1（s）是采样时间，fb（k）（N/kg）表示单位质量上的基本阻力，fa（k）（N/kg）表示特定线路中单位质量上的附加阻力。

式中，a（k）是滚动阻力系数；b（k）是与摩擦和列车振动相关的阻力系数；c（k）是空气动力阻力系数。

对于IMFAILC-DLLC 迭代学习控制、RBFDLLC 迭代学习控制和无模型自适应迭代学习控制，高速列车的速度跟踪性能分别如图5～图8 所示，其中，vd为高速列车的期望速度。

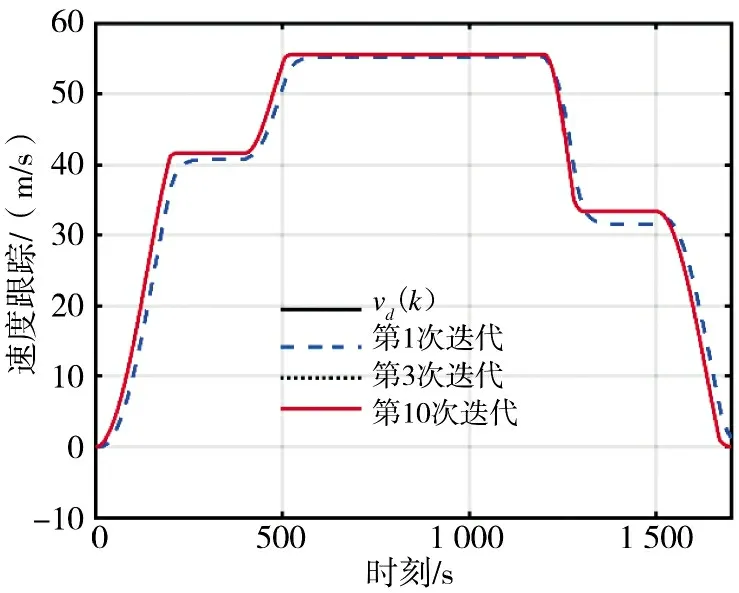
图5 IMFAILC-DLLC ILC 跟踪性能Fig.5 Tracing performance of IMFAILC-DLLC ILC

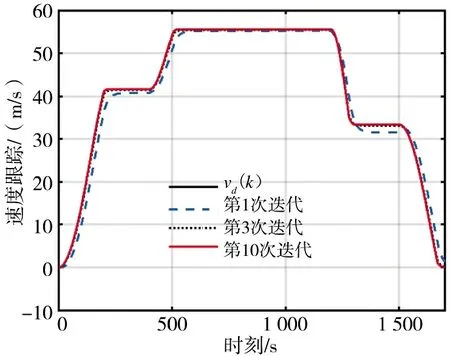
图6 RBF-DLLC ILC 跟踪性能Fig.6 Tracing performance of RBF-DLLC ILC

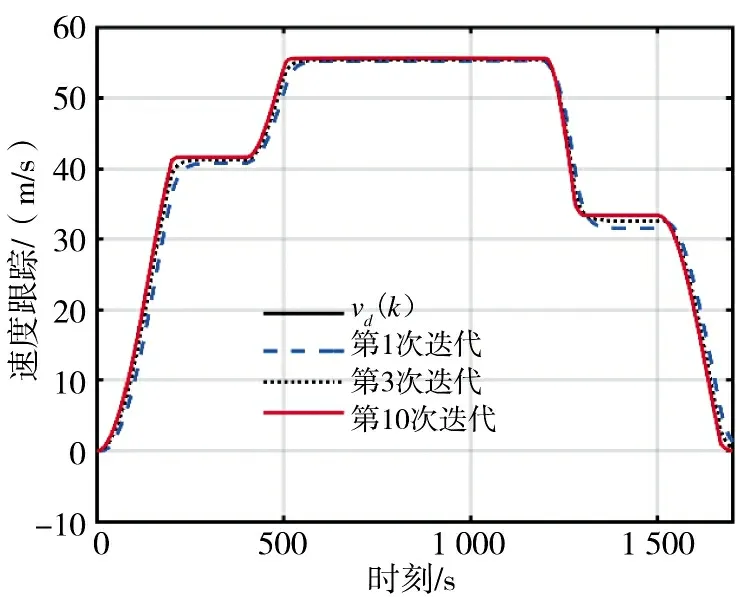
图7 MFAILC 跟踪性能Fig.7 Tracing performance of MFAILC

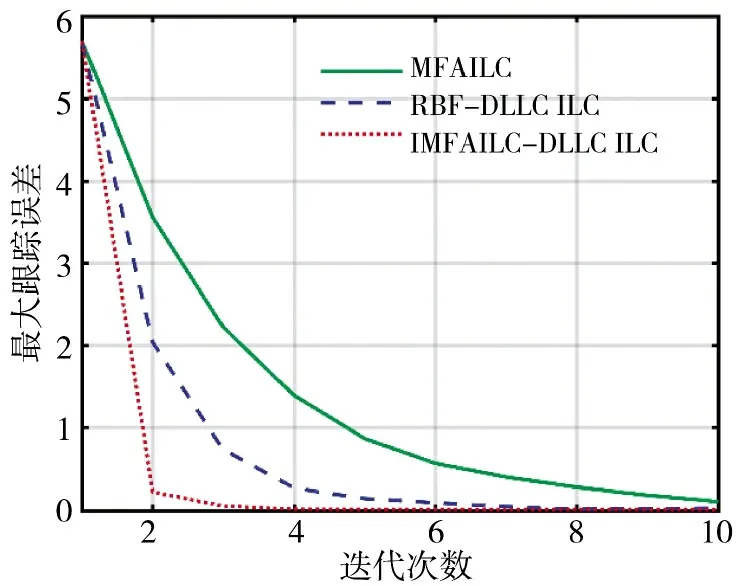
图8 迭代过程最大误差Fig.8 Maximum error of iterative process

仿真结果表明，迭代3 次后，3 种迭代学习控制方法都表现出了出色的跟踪性能，经过10 次迭代后，IMFAILC-DLLC 迭代学习控制和RBF-DLLC 学习控制的收敛误差分别从大于5 m/s 降低到小于0.015 m/s，以及从大于5 m/s 降低到小于0.03 m/s，而MFAILC 的收敛误差在10 次迭代后仍大于0.1 m/s，如图8 所示。实验还表明，经过10 次迭代后，IMFAILC-DLLC 迭代学习控制和RBF-DLLC 迭代学习控制的收敛误差接近。由此可以看出，对于控制输入饱和的高速列车模型，所提出的IMFAILCDLLC 迭代学习控制比RBF-DLLC 迭代学习控制和自适应迭代学习控制具有更好的跟踪和学习性能。

4 结论

本文研究了一种新的数据驱动迭代学习控制方案。通过将DL 技术应用于迭代域中的未知理想学习控制器，系统地设计了具有动态结构的迭代学习控制律。应用改进的无模型自适应迭代学习控制算法，对包含在学习控制增益向量中的受控系统的非线性进行估计，仿真结果表明，所提出的数据驱动迭代学习控制方案具有优异的跟踪性能和良好的收敛速度。