基于半监督聚类方法的管道运行状态识别研究

2023-06-25方明月冯早朱雪峰

南京大学学报(自然科学版) 2023年3期

方明月 ,冯早* ,朱雪峰

（1.昆明理工大学信息工程与自动化学院，昆明，650500；2.云南省矿物管道输送工程技术研究中心，昆明，650500）

在现场环境数据采集中，随着数据采集设备与存储设备的推陈出新，数据的获取不再困难，简单的重复实验即可获得大量的无标签数据.同时，由于一些先验知识、专家经验等原因，只有小部分数据带有监督信息，如果仅仅用这些数据进行监督学习，过少的标记数据量往往会导致学习器过拟合、对新样本的适应能力不足.对数据进行标注会花费很多时间，增加实验的支出；若通过传统的无监督学习方法实现聚类，则会导致难以获取的监督信息的利用率大大降低［1］.半监督学习利用数据集中仅有的监督信息指导学习器对剩下的无标签数据集进行分类，避免了学习器仅利用数据集中单一局部信息而出现的问题，但却增加了半监督学习器对监督信息的依赖性.

针对半监督学习对监督信息的依赖性问题，如何筛选监督信息以达到少量的监督信息即可完成有效的半监督学习的目标以及减少监督信息中噪声样本对半监督学习器的影响等，成为半监督学习研究的热点.另外，在半监督学习中还经常遇到样本数量过少和样本间数量不均衡的问题，如何在小样本数据或不均衡数据下实现半监督学习亦是当下的研究热点.如史蕴豪等［2］提出一种基于伪标签的半监督学习技术的小样本调制方式分类算法，解决在只包含少量标签样本时存在的通信信号识别度不高的问题；杨宇等［3］提出基于增量式半监督多变量预测模型，有效地解决了小样本的故障诊断问题，并缩短了分类时间.

半监督学习的全面发展为半监督聚类奠定了良好基础，半监督聚类在道路检测、医学、图像、故障诊断等领域取得了一定进展.如张建朋等［4］提出进化因子图模型，弥补传统聚类只从静态图出发难以满足建模动态变化的真实网络图的要求.刘少鹏等［5］提出一个以半监督为基础的对抗网络的分阶段混合模型，用以解决医学领域中带有标签的数据较少导致的不足以完成神经网络模型的训练的问题，获得了良好的医学图像分割效果.

针对上述实测数据不包含标记信息、少量监督信息只能从专家经验对部分样本的赋予和从实验室已有监督信息中获得、监督信息的利用通常具有随机性等问题，本文提出一种主动学习策略下基于变分贝叶斯推理的半监督高斯混合模型：

（1）通过主动学习策略建立高质量成对约束条件，实现了标记信息的有效利用，提升了半监督变分贝叶斯推理高斯混合模型（下文均简称为半监督高斯模型）的学习性能.

（2）在实验中不断减少标记样本的数量，探索标记样本数量对模型的影响.为了进一步提升模型在标记样本数量不断减少时的识别准确率，还在模型中引入最小生成树聚类对半监督高斯模型的主要参数进行初始化，提升模型在面对标记样本数量不断发生变化时的稳定性.

（3）当某一类别的标记样本数量减少到0，即完全缺失该类别的标记信息时，本文提出的主动学习策略下基于最小生成树的变分贝叶斯推理半监督高斯混合模型依旧可以实现有效的判别.

1 相关算法

1.1 半监督聚类半监督聚类将类标签或成对约束等先验知识融入传统聚类方法来获得更高质量的聚类结果.根据先验知识的不同，半监督聚类大致可分为基于距离的半监督聚类方法和基于约束的半监督聚类方法.

基于距离的半监督聚类方法利用数据集中一些标记数据来指导聚类机制.Wu et al［6］设计了一种基于密度敏感的半监督聚类法，得到一种改进的密度敏感的距离度量，可以有效地增大位于不同稠密区域的样例的距离，并缩小位于同一稠密区域内的样例的距离.Bijral et al［7］以基于密度的距离估计为基础，提出一种用图上的最短路径进行计算的简单有效的方法，适用于稠密的全连接图，能有效地减少运行时间.范九伦等［8］提出半监督截集式可能性C‐均值聚类算法，提高彩色图像分割的效率和准确率.基于距离的半监督聚类方法的缺点是其聚类效果很大程度上依赖于标签数据集的规模和质量.

基于约束的半监督聚类方法在为簇分配数据时利用监督信息来限制可行解，或直接通过改变分配策略来防止违反监督信息的分配［9］，或在监督信息被违反、得到满足的情况下，通过惩罚、奖励目标函数间接进行，缺点是求解时易出现约束违反的情况.刘如辉等［10］通过建立成对约束关系，将快速密度峰值聚类算法引入半监督学习，结合集成学习的思想解决原算法中的自动选择时误选和漏选中心点、簇的数量需要主观先验判断、算法使用受场景局限等缺陷.张鑫等［11］在拉普拉斯特征映射算法的基础上，对标记样本点进行置信度约束，提出基于改进的拉普拉斯特征映射算法的半监督故障诊断模型，优化了聚类效果.

1.2 基于主动学习策略的成对约束筛选为了提高聚类性能，一般将先验知识加入无监督聚类算法来提升聚类的效果，进而提出一系列改进的半监督聚类算法.最常见的先验知识有两种：一是标签信息；二是存在于数据点之间的成对约束信息，即必连约束和勿连约束［12］.必连约束是隶属于相同类型的成对的数据，而勿连约束是隶属于不同类型的成对的数据.

一般地，在半监督聚类算法中，若被提供的监督信息占总的数据信息的比重较小，或者该类信息是聚类算法自身可以捕捉的，会导致该类信息不易指导算法完成聚类，难以提升算法的性能［13］.因此，需要找到只通过算法自身很难发现的数据间的密切联系，利用该数据关系可以获取信息规模更大的监督信息，而这些信息对提高半监督聚类学习器的聚类性能大有裨益.

如图1 所示，用三角形和圆形两种不同形状分别表示两种不同类型的数据，其中勿连约束用红色虚线表示，必连约束用黑色实线表示.图1a中，构成必连约束的数据点空间位置相邻甚至出现重叠情况，而构成勿连约束的数据点之间相距较远，聚类算法总是将构成必连约束的数据集分到同一类别中，将构成勿连约束的数据集归为不同类别，导致先验知识失去了对聚类算法的指导作用，得到的监督信息是无效的、低质量的.图1b中的约束集与图1a 相反，同类别之间距离较远的点构成了必连约束，不同类别之间距离较近的点构成了勿连约束，这样可以更充分地体现数据之间的结构，而仅仅通过聚类算法难以发现这个结构.因此，通过这种方式得到的数据一般具有较高的信息量.

图1 监督信息特性的示例Fig.1 Examples of supervisory information characte⁃ristics

建立高质量成对约束的主动学习策略以数据集D(r*c)（r为样本数，c为特征维数）和已有的成对约束集为基础，其中输入为已有的必连约束集和勿连约束集，输出为新的必连约束集和勿连约束集.该策略的伪代码如算法1 所示，其中，D_ML，D_CL 分别表示必连约束距离和勿连约束距离，T表示迭代次数，vx，vy分别表示Q中数值对应到矩阵D中的两个数.

1.3 主动学习策略下基于最小生成树的变分贝叶斯推理的高斯混合模型基于谱图的最小生成树半监督聚类主要依赖距离矩阵，将每个顶点看作一个独立的树，在满足约束条件下依据距离合并最小生成树以达到聚类目的，直至最后聚类簇数小于等于目的类簇数为止.其输出为类别标签，这些标签信息被用来对变分贝叶斯推理的高斯混合模型中的参数（均值、协方差以及混合系数）进行初始化.

2017 年Blei et al［14］提出变分高斯混合模型（Variational Bayesian Inference for Gussian Mix‐ture Model，VBIGMM），应用于无标记样本数据集.假设从K个独立的高斯分本中抽出n个样本，xi为一个样本数据，uk为每个高斯分布的均值，ci表示样本xi对应的高斯分布.则高斯混合模型的生成过程［15］如下：

根据平均场的性质，每个潜在变量都由其自身的变分因子控制.因子q(uk；mk；)是第k个混合组件均值参数的高斯分布，其平均值为mk，方差为.因子q(ci；φi)是第i个观测值混合分配，其分配概率为K维向量φi.

变分贝叶斯推断的目标是寻找一个恰当的联合分布使其近似代替P(x)，即最大化变分下界ELBO.ELBO越大，近似估计的概率分布和数据整体真实的概率分布的相似度就越高.

为了合理利用监督信息，在上述变分贝叶斯推理高斯混合模型中引入必连约束和勿连约束.在推理过程中，勿连约束使具有不同标签的样本不能分配给相同的高斯分量，必连约束使具有相同标签的样本不能分配给不同的高斯分量.

主动学习策略下基于最小生成树的变分贝叶斯推理的高斯混合模型以数据集与新的必连约束集和勿连约束集作为输入，以数据的标签向量作为输出.该算法的伪代码如算法2 所示，其中，N表示簇数，P表示概率矩阵，G表示无向权重图，su和sv分别表示构成G中边的两个点，uk表示均值，ce表示质心，Mc表示协方差矩阵.

2 技术路线

由于实验室采集的管道状态检测声学信号数据集的监督信息是标签信息，而不是本文要求的成对约束信息，因此首先需要根据实验提供的标签信息随机构建必连约束集与勿连约束集，作为本文半监督实验中的初始监督信息.

步骤1.信号分解：对检测到的管道运行状态声学响应信号进行互补集合经验模态分解（Com‐plementary Ensemble Empirical Mode Decomposi‐tion，CEEMD），经过信号分解后获得八个内涵模态分量（Intrinsic Mode Functions，IMF）.

步骤2.特征分量的选取：计算分解后的八个IMF 分量和原始声压信号的皮尔逊相关系数，系数越大表示分量与原信号的相关性越强.本文需要选取相关性较强、特征信息丰富的IMF 分量.

步骤3.特征提取：分别计算步骤2 中选取的IMF 分量的过零率与梅尔频率倒谱系数（Mel‐Scale Frequency Cepstral Coefficients，MFCC），构建特征向量集合D.

步骤4.主动学习策略：将特征向量集合D与必连约束集合、勿连约束集合输入基于主动学习策略的成对约束筛选模型，一般认为不同类中距离最近的两个样本点构成的勿连约束与同类中距离最远的两个样本点构成的必连约束提供的信息难以被聚类算法本身捕捉，属于高质量约束信息.输出新的高质量必连约束集合和勿连约束集合.

步骤5.半监督最小生成树聚类：将特征向量集合D与新的高质量必连约束集合和勿连约束集合输入半监督最小生成树聚类.将每个样本看作独立的树，在满足约束条件下，根据样本点之间的欧式距离进行样本划分，直到规定的簇数，计算聚类后每个簇中簇心和协方差矩阵.

步骤6.半监督变分推理高斯混合模型：依据步骤5 的结果依次初始化模型中的均值向量和协方差矩阵，再将特征向量集合D与新的高质量必连约束集合和勿连约束集合输入模型，根据样本点分属类别的概率矩阵的最优值为所有样本赋予标签，发生约束冲突时选择次优值，最后输出聚类标签向量.

步骤7.聚类评价：使用准确率来评估聚类效果，验证本文提出的模型的有效性.

本文的技术路线流程如图2 所示.

图2 技术路线的流程图Fig.2 The flow chart of experimental method

3 实验平台与数据采集

采用实验室搭建的管道运行状态检测平台获取实验数据集来学习并验证模型的性能.该平台包括一段直径为150 mm、长14.4 m 的黏土管道，东方所INV3062T 信号采集仪，爱华AWA1651声源发生器，智众叁H5646 信号放大器，奥乐YJB‐10 扬声器，东方所INV9206 声压传感器.

3.1 实验过程

（1）在管道首端放置声压传感器和信号采集仪以及声源发生器，声源发生器选择100～6000 Hz 的正弦扫频信号作为激励信号.

（2）将声源发生器的一端连接信号采集仪来获取输入信息，另一端连接信号放大器，激励信号经过放大之后满足扬声器的信号频段需求，经其转变为声音信号，实现声音在管道中的传播.

（3）将四个声压传感器顺序排列放置在管道尾端，将各通道传感器采集的声压信号通过数据采集仪输入电脑，进行存储和下一步处理.

对实验过程中管道的堵塞程度定义为：如果堵塞物在管道中的堵塞高度达到管道直径的三分之一，定义为重度堵塞；没有达到该高度则定义为轻微堵塞.因此，为了分别模拟现实管道中的轻微和中重度堵塞，实验过程中在管道中放置高度分别为20 mm 和55 mm 的堵塞物，并且，为了确定管道运行时旁支管道对整个检测结果的干扰程度，使用三通件来模拟旁支管道.管道堵塞实验模拟平台如图3 所示.

图3 实验平台、三通件和堵塞实物图Fig.3 Physical diagrams of experimental platform，three⁃way piece and blockages

3.2 数据采集采样频率设定为44100 Hz，根据声音在空气中的传播速度及待检测管道长度将采样时间设定为0.1 s.模拟的管道运行状态包括正常健康的管道、含三通件的正常健康管道、含有轻微堵塞物的管道和含重度堵塞物的管道四种，采集四种工况下的声学响应信号数据各144组，得到的信号的时域波形如图4 所示.由图可见，四种工况的区分性较差，难以实现工况的识别.

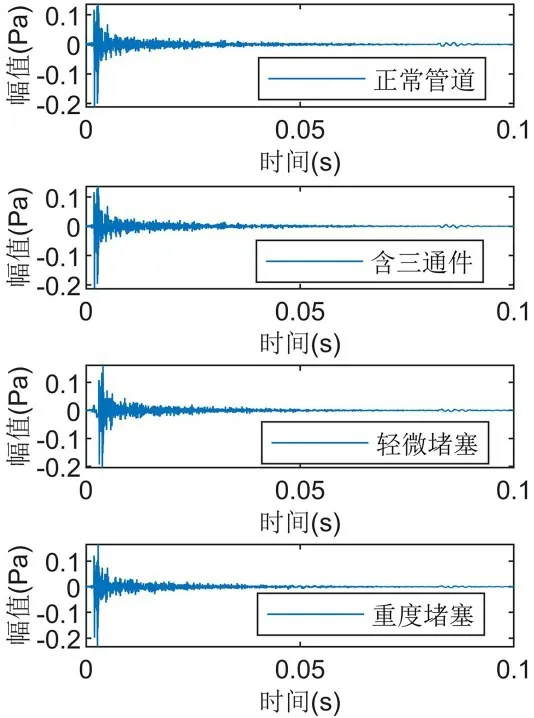
图4 四种工况下的管道时域波形图Fig.4 Time domain waveforms of pipeline under four working conditions

4 数据处理与特征提取

4.1 CEEMD 分解2010 年Yeh et al［16］针对集合经验模态分解（Ensemble Empirical Mode De‐composition，EEMD）算法在引入的白噪声集总平均之后不能完全抵消而存在残留、重建的分量信号依旧存在不可忽略的噪声等问题，提出互补集合经验模态分解（Complementary Ensemble Em‐pirical Mode Decomposition，CEEMD）算法.

算法的流程如下：

Step 2.经验模态分解（Empirical Mode De‐composition，EMD）：加入噪声2n个信号(t)和(t)，得到2n个集成的IMF 分量，分别为IMFi1和IMFi2.求IMFi1和IMFi2的均值得到IMFi，再计算n组的IMFi，得到最终的IMF 分量.

4.2 信号分解对四种不同工况的声学信号进行CEEMD 分解，图5 以20 mm 堵塞故障采集得到的信号为例，给出了声压信号经CEEMD 分解后获得的八个IMF 分量信号的不同特征成分.由于不同分量包含的信息成分不同，为了提高下一步的模型学习效率，还需要对分量进行筛选.

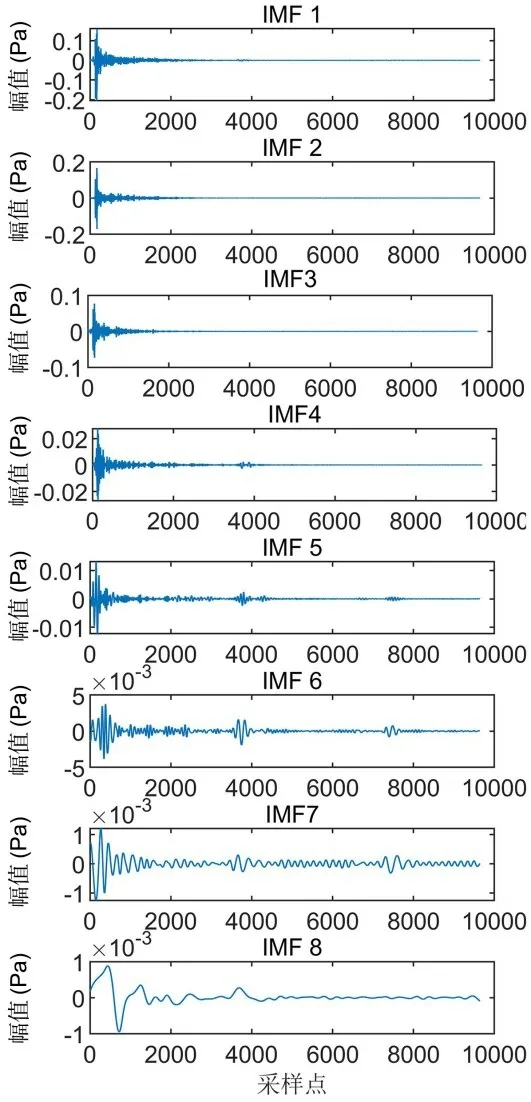
图5 IMF 分量的时域波形图Fig.5 Time domain waveform of IMF component

4.3 IMF 分量筛选分别计算各分量信号与原信号之间的皮尔逊相关系数，将得到的不同系数进行排序后选取合适的分量构建半监督学习模型的训练特征集.

皮尔逊相关系数是1895 年Pearson［17］提出的度量两个变量之间相关程度的一种统计概念，其值介于-1 与1 之间.本文用来衡量各分量信号与原信号的相关程度，一般认为皮尔逊相关系数r<0.1时，两者不相关.

向量X{x1，x2，…，xn}与Y{y1，y2，…，yn}之间的皮尔逊相关系数为：

经CEEMD 分解后的八个分量信号与原信号的皮尔逊相关系数如表1 所示.由表可见，分量信号IMF6，IMF7，IMF8 与原信号的皮尔逊相关系数均低于0.1，因此认为IMF6 以后的分量信号与原信号极弱相关或无相关.所以，选取分量IMF1～IMF5 进行特征提取.

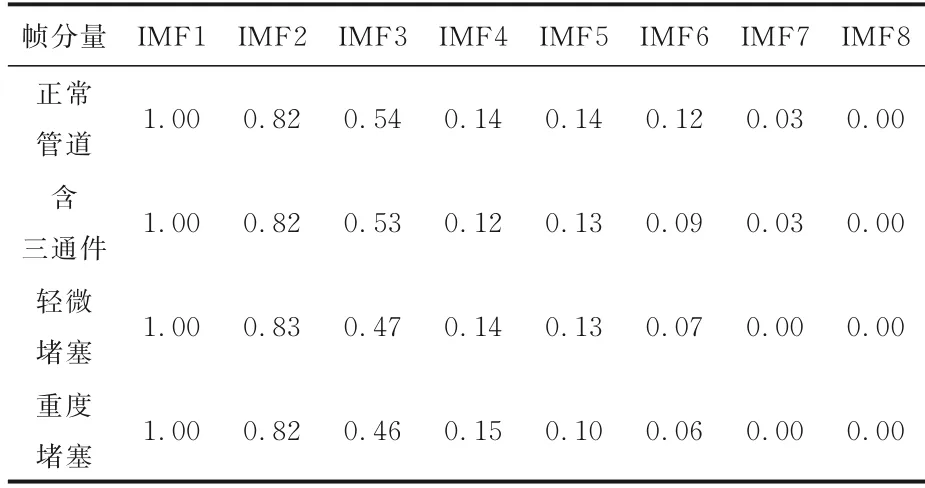
表1 各分量信号与原信号间的皮尔逊相关系数Table 1 Pearson correlation coefficient between each component signal and the original signal

4.4 特征提取对于选取的IMF1～IMF5 分量，分别计算其过零率与梅尔频率倒谱系数，构建能够描述管道状态的声学特征集.

4.4.1 过零率过零率指一个信号通过零点的次数，主要应用在模式识别和声纹检索等领域，如杨亦春等［18］将过零率分析引入声引信目标信号分析与识别，孙慧芳等［19］利用过零率和幅值频谱提升语音和音乐分类识别的准确率.过零率也常被应用到其他领域，如尹丽等［20］将过零率应用到波形复杂且幅值较小的心电信号分析中，刘琨等［21］认为过零率能够较好地体现信号的部分频率信息，将其应用到多类别入侵事件识别方法中.

过零率的计算如式（13）所示：

其中，threshold为设定的阈值，本文中设为0.

sgn(x)的计算如式（14）所示：

4.4.2 梅尔频率倒谱系数梅尔频率倒谱系数（MFCC）在声音信号处理中常作为信号特征被广泛使用，基于MFCC的研究大量涌现［22-23］.MF⁃CC的提取方法主要分两步：第一步，通过常见的离散傅里叶变换将信号映射到频域，计算能量谱；第二步，用一组Mel 尺度的三角形滤波器对得到的能量谱进行卷积运算，实现滤波处理.为了便于对信号进行倒谱分析，对结果取对数，最后通过离散余弦变换得到24 维的关于声信号的特征参数.

5 半监督聚类与结果分析

5.1 主动学习策略为了证明主动学习策略对半监督聚类的积极影响，设计的初始成对约束由每个类别的标签样本随机构建必连约束集和勿连约束集，每个类别的标签样本含量占该类别样本数量的50%.在基于成对约束的半监督变分推理高斯混合模型上验证由主动学习策略筛选成对约束的有效性.有主动学习策略的模型将主动学习策略筛选后的新的必连约束集和勿连约束集作为模型的输入，无主动学习策略的模型将初始约束集合作为模型的输入.使用准确率评估实验结果，实验100 次后对所有结果取平均值，将其作为展示结果.实验结果如图6 所示，类别1，2，3，4 分别对应正常管道样本、含三通件的管道样本、含轻微堵塞的管道样本和含重度堵塞的管道样本，预测类别为0 的样本是模型判断失效的样本.

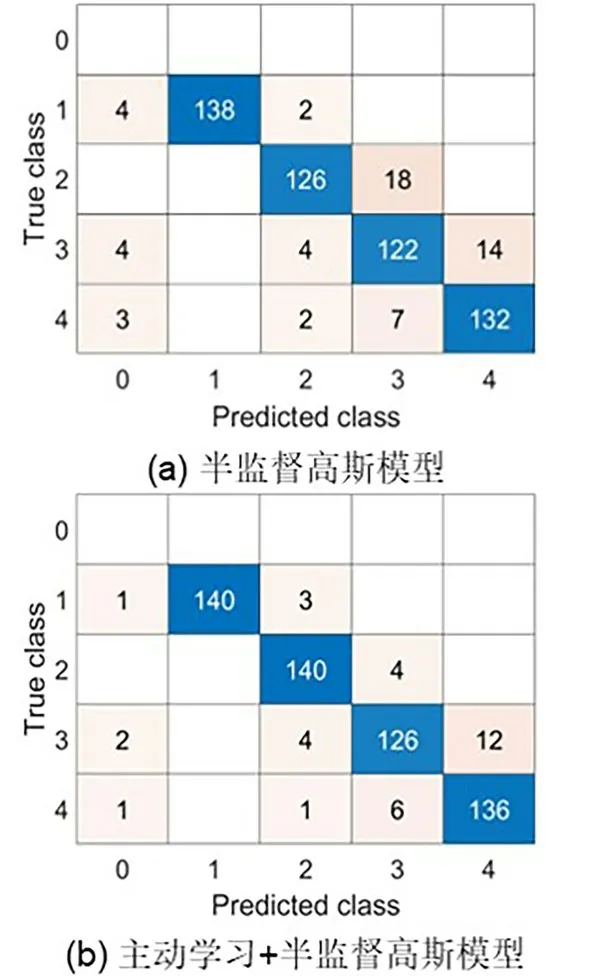
图6 主动学习策略的模型图Fig.6 The diagram of active learning strategy model

图6a 是将基于变分推理的高斯混合模型在增加成对约束后，再引入半监督学习得到对管道运行状态识别的混淆矩阵，可以看出该模型有效地根据少量的标记信息辅助模型训练无标记数据.通过主动学习策略构建的高质量约束集可以提供聚类算法本身不易发掘的信息，进一步提升模型的识别准确率，其混淆矩阵如图6b 所示.对比图6a 和图6b，可以看出，增加主动学习策略后模型类别的识别准确率至少提高了3%，模型判断失效样本减少了72%.

5.2 半监督学习组合方法

5.2.1 监督信息减少时半监督学习模型性能对比为了进一步验证半监督模型在监督信息比例发生变化时的学习性能，对实验数据中每个类别提供的标签样本量与该类别样本数量的百分比进行调整，从初始的50% 下降到10%，每次下降10%.初始必连约束集合和勿连约束集合依据实验数据中提供的标签信息随机构建.分别在半监督高斯模型、加入主动学习策略的高斯模型以及加入主动学习策略的基于最小生成树的变分贝叶斯推理半监督高斯混合模型（下文均称为组合模型）中进行实验，实验结果如图7 所示.

图7 不同标签含量的半监督高斯模型对比Fig.7 Comparison of semi⁃supervised Gaussian mod⁃els with different label contents

由图可见，随着标签样本含量的下降，增加了主动学习策略的半监督高斯模型的准确率在不断降低.比例为10%时，主动学习策略对模型的聚类性能改善有限，而使用了组合聚类的模型性能优于其他两个模型，也更稳定.

5.2.2 当某一类别无监督信息时模型性能分析依次取消各类别中所有的标记信息，当某个类别完全无标签信息时，其他类别的含标签信息的样本数量占总样本标签数量的50%.聚类时将完全无标签信息的样本类别定义为无预定义标签类，即0 类.实验中所需的初始成对约束监督信息依旧根据实验所提供的标签信息随机构建，这种情况得到的实验结果如图8 所示.

图8 不同情况下的完全缺失部分类别标记信息的聚类结果Fig.8 Clustering results of completely missing partial category marker information in different cases

由图可见：（1）完全缺失正常管道的类别标记信息时，模型识别的准确率达92.4%，该类别与其他类别间有极弱的相似性，故而被识别为新类别的准确率较高.（2）完全缺失含三通件管道的类别标记信息时，模型的识别为新类别的准确率可达70.8%.由于声波在含三通件的管道中传播不存在堵塞时，其传播路径与正常管道中传播路径类似过程相似，但声波又会在三通件的位置发生部分散射和反射现象，此时与声波在管道中遇到堵塞物时发生的物理现象又有部分类似，因而完全缺失该类别的标记信息时会有10%～20%的样本被错分为正常管道和轻微堵塞.（3）完全缺失堵塞管道的类别标记信息时，系统识别为堵塞的准确率可达73.6%.声波在管道中遇到堵塞物时发生的物理现象相同，但堵塞物的高度不同，传感器接收的声压信号会有差异，实验中管道中的轻微堵塞物和重度堵塞物的高度仅相差3.5 cm，因而，在不同堵塞程度的管道类别标记信息为0 需要进一步判断堵塞程度时，模型在判断该类别为新类别的同时，容易将该类别的部分样本误判为其他堵塞程度的管道类别.