矩形开孔沉箱防波堤可靠性分析❋

2023-06-25姜逢源

中国海洋大学学报（自然科学版） 2023年7期

张鑫, 姜逢源, 董胜

(1. 中国三峡新能源(集团)股份有限公司, 北京 101100; 2. 中国地质大学(武汉) 海洋学院, 湖北武汉 430074;3. 中国海洋大学工程学院, 山东青岛 266100)

在实际工程中,不确定性通常来源于对外部荷载、几何参数、材料性质、边界条件及建造过程的不完全控制[1]。以概率论为基础,对上述不确定性加以智慧的反映,便构成了结构随机分析的基本概念与理论框架。其中结构可靠性分析作为该框架的有机组成部分,在结构的设计、安全性评价和重大工程的决策等领域得到广泛应用[2]。通过用概率定量表示出结构可靠性的大小,可保证结构具有足够的安全水平[3]。经过多年的发展,以概率统计为基础的可靠性分析,已形成一些公认较有效的方法,总体而言可以分为三大类:近似解析方法、数字模拟法和基于代理模型的方法。20世纪80年代中期,结构可靠性设计方法开始应用于防波堤的设计中[4]。

防波堤处于近海,受风暴、波浪、海流、气象、地震、地质和地貌等复杂环境因素影响,在这些环境因素中波浪是最主要的因素[5]。防波堤作为关键的海岸建筑物,其首要作用是抵御波浪对港域的侵袭,保证港口具有平稳的水域[6]。谢世楞和刘颖[7]基于作用于直立堤上不规则波浪力的实验资料,对直墙式防波堤的可靠性设计方法进行了研究,得出总波浪荷载(水平波浪力、浮托力)的长期分布服从对数正态(Log-normal)分布和极值Ⅰ型(Gumbel)分布。郄禄文等[8]基于变量相关的Hasofer-Lind方法[9],采用长期波浪实测资料,分析了削角直立式防波堤进行了可靠性。张磊等[10]采用直接积分法分析计算了直墙式防波堤的失效概率。张向东等[11]基于人工神经网络理论分析了直墙式防波堤的可靠性。刘君等[12]提出基于样本累计的响应面法,对某核电工程防波堤的稳定性进行了分析。Koç等[13]提出了一种基于云理论的模糊随机可靠度分析方法,并通过3个防波堤算例对该方法的适用性进行了研究。李静静等[14]提出了基于Copula函数通过直接积分计算分析直墙式防波堤可靠性的方法。

矩形开孔式防波堤是直立式防波堤的一种改进型式,最早于20世纪60年代由Jarlan[15]提出,在实际设计建造中,是将矩形沉箱的前墙上部开孔,使沉箱的部分前舱形成消浪室,具有减小波浪反射、降低总波浪荷载、节省原料和降低工程投资费用等优点,其在港口建设中已被较多的应用,既能满足实际功能需要,又取得了良好的经济效益[16]。以往,在直立堤的可靠性分析中,最主要问题是确定波浪荷载的统计参数和分布型式以及选择计算可靠指标的方法[17],通常需要构造波浪荷载与抗力的功能函数;而在实际工程中,波浪荷载作为中间变量,其变化来自于波浪要素的不确定性。

为研究矩形开孔沉箱防波堤的可靠性,提出了一种适用于直立式防波堤可靠性分析的新方法(见图1):不同于以往传统方法中将波浪荷载和抗力作为随机变量处理,文中考虑波浪要素的相关性,将波浪要素(波高、周期)和抗力(自重、摩擦系数)作为随机变量处理,构造隐式功能函数,采用直接抽样法生成随机样本进行模拟,作为中间变量的波浪荷载不做统计分析处理,根据功能函数的响应直接判断是否滑移或倾覆失效,计算失效概率和可靠指标,更加符合工程实际。

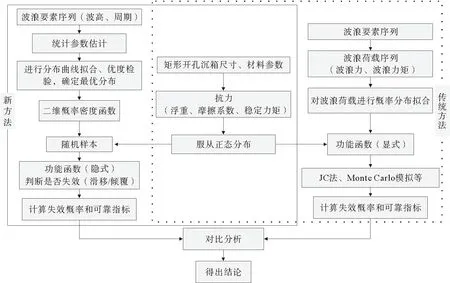
图1 分析流程图Fig.1 Flowchart of the analysis

1 可靠性分析方法

在评价防波堤结构的可靠性时,主要考虑特征波浪力的长期分布关系。堤身浮重G及其对后趾的稳定力矩MG服从变异系数V=0.05的正态分布分布;堤身与基床的摩擦系数f服从正态分布,均值为μf=0.06,标准差σf=0.026[18]。常用的单因素极值分布模型有:Log-normal分布、Weibull分布及Gumbel分布[19]。传统方法中的波浪荷载和新方法中的波高、周期均需要通过分布曲线拟合和拟合优度检验确定最优分布类型。本文通过分析同传统方法,判断新方法的有效性。

1.1 传统分析方法

传统分析方法计算流程如图2所示。

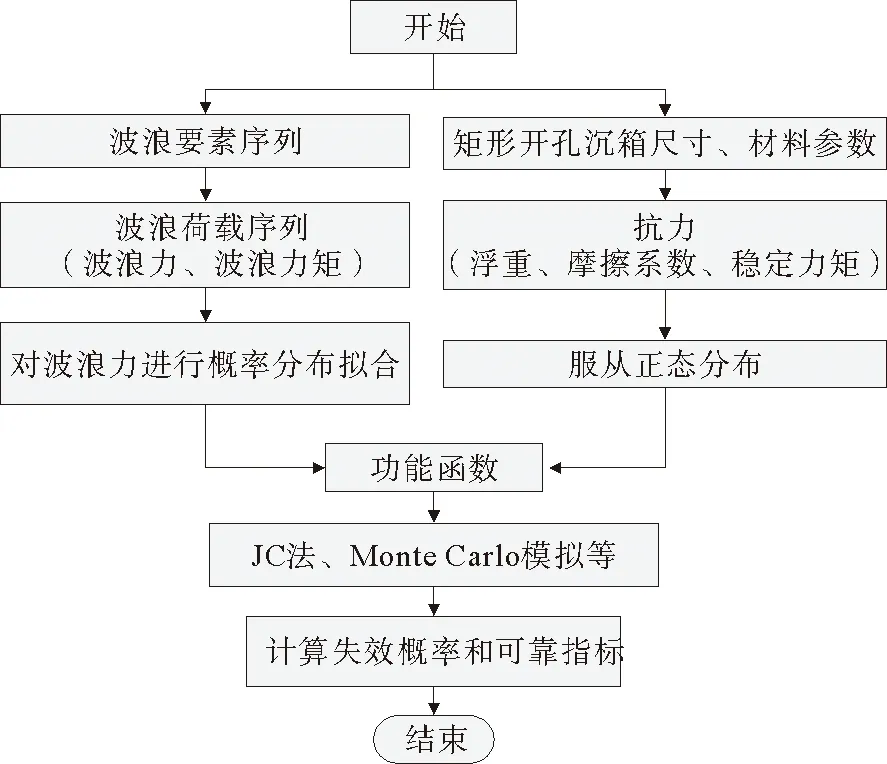
图2 传统分析方法计算流程图Fig.2 Calculation flowchart of traditional analytical method

防波堤受到的波浪压力分布如图3。

图3 修正Goda公式的波浪压力分布图Fig.3 Wave pressure distribution in accordance with the modified Goda pressure formula p1=0.5(1+cosθ)(λ1α1+λ2α*cos2θ)γHd,

(1)

(2)

p3=α3p1,

(3)

p4=α4p1,

(4)

pu=0.5(1+cosθ)λ3α1α3γHd,

(5)

(6)

(7)

(8)

(9)

η0=0.75(1+cosβ)λ1Hd,

(10)

α*=max{α2,αI} 。

(11)

防波堤滑动稳定失效功能函数gs的计算公式为:

gs(PH,PV,G,f)=(G-PV)·f-PH。

(12)

式中:PH、PV分别表示矩形开孔沉箱防波堤所受总的水平波浪力 (kN/m)和竖直波浪力(kN/m),均为随机变量;G表示防波堤的浮重(kN/m),为随机变量;f表示防波堤堤身底面与基床的摩擦系数,为随机变量。

防波堤倾覆失效功能函数gc的计算公式为:

gc(MPH,MPV,MG)=MG-MPH-MPV。

(13)

式中:MPH和MPV分别表示矩形开孔沉箱防波堤所受水平波浪力和竖直波浪力对防波堤后趾的力矩(单位:kN·m/m),为随机变量;MG表示防波堤堤身浮重对后趾的稳定力矩(单位:kN·m/m),为随机变量。

对于传统的分析方法,功能函数为显示表达,求解关键是分析确定波浪荷载和抗力的统计参数和概率分布函数。可以直接使用近似解析法和Monte Carlo模拟多种方法求解可靠度。

1.2 新分析方法

新方法在构造极限状态方程时,将波浪要素波高、周期、自重和摩擦系数作为初始随机变量处理,考虑波高、周期的相关性,不再处理作为中间变量的波浪荷载,直接得到功能函数响应,判断防波堤是否发生滑移或倾覆失效。

防波堤滑动稳定失效函数和倾覆失效功能函数的新计算公式为:

g(H,T,f,G)=[G-PV(H,T)]·f-PH(H,T),

(14)

g(H,T,MG)=MG-MPH(H,T)-MPV(H,T)。

(15)

式中:H、T分别为波高(单位:m)、周期(单位:s),为随机变量,二者具有相关性;函数PH、PV分别表示矩形开孔沉箱所受的水平波浪力、竖直波浪力,均为中间变量,不需要进行统计处理;函数MPH和MPV分别表示水平波浪力、竖直波浪力对堤身后趾的力矩,均为中间变量,不需要进行统计处理。f表示防波堤堤身底面与基床的摩擦系数;G表示防波堤的浮重;MG表示防波堤堤身浮重对后趾的稳定力矩。F、G和MG相互独立且与波高、周期相互独立。

对于新分析方法,功能函数为波高H和周期T的隐式表达,无法得到其对于波高H、周期T的偏导数,导致不能使用近似解析法及基于近似解析法发展而来的几种Monte Carlo重要抽样方法等,可采用直接Monte Carlo模拟或代理模型如人工神经网络法、响应面法和克里金插值法等。本文采用直接Monte Carlo模拟方法,能够有效解决隐式和高度非线性可靠性问题,计算流程如图4。

图4 新分析方法计算流程图Fig.4 Calculation flowchart of new analytical method

直接Monte Carlo模拟方法计算失效概率pf公式为:

(16)

式中:Ωf为失效域;fX(x)为随机变量X的联合概率密度函数;gX(x)为随机变量X的失效功能函数,根据随机变量X的联合概率密度函数fX(x)对X进行随机抽样;I[gX(x)]为gX(x)的示性函数,并规定当gX(x)<0时为I[gX(x)]=1,gX(x)≥0时为I[gX(x)]=0。通常推荐随机样本量

(17)

当各分量Xi相互独立时,对X的抽样等价于独立的对每个元素进行抽样。考虑随机变量间的相关性时,有Cholesky分解、特征值分解、Rosenblatt变换、Nataf变换和Copula函数法等。本文采用Copula函数法,基于G-H Copula函数构造联合分布,生成二维随机数。

2 矩形开孔沉箱防波堤的波浪荷载

目前推荐在工程上应用的3种方法:中国《防波堤设计与施工规范》推荐的由大连理工大学团队提出的经验公式[20];日本学者高桥重雄[21]给出的计算方法;法国Tabet-Aoul 和 Lambert[22]给出的计算方法。中国规范推荐公式受波浪形态和基床类型限制,而Tabet-Aoul 和Lambert’s方法只给出了水平波浪力的经验公式,所以本文中关于波浪荷载的计算采用的是高桥重雄的方法,总波浪力和波浪力矩由波浪力强度沿作用区域积分得到。

该方法中波浪荷载的计算是基于带有修正参数λ1、λ2和λ3的Goda方法:λ1代表缓慢变化波压力部分的修正参数;λ2代表水平方向冲击波压力部分的修正参数;λ3代表浮托力部分的修正参数。该方法中波浪荷载的计算是基于带有修正参数λ1,λ2和λ3的Goda方法,λ1代表缓慢变化波压力部分的修正参数,λ2代表水平方向冲击波压力部分的修正参数,λ3代表浮托力部分的修正参数。图5为波峰Ⅱb状况下开孔沉箱压力分布图,λS代表前墙的透空部分的修正参数,λL代表前墙实体部分的修正系数,λR代表消浪室后实体墙的修正系数,λM代表消浪室底板的修正系数,λU代表浮托力的修正系数,B为消浪室宽度。各部分的修正系数详见表1。

表1 波浪与开孔沉箱相互作用的修正参数表Tabel 1 Modified parameters of wave and perforated breakwater interaction

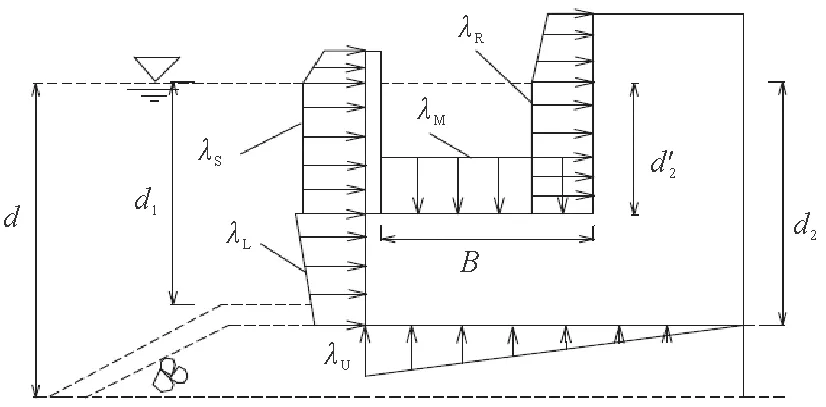
图5 波峰Ⅱb状况下开孔沉箱压力分布图Fig.5 Wave pressure distribution at Crest-Ⅱb phase for a perforated wall breakwater

图6 矩形开孔沉箱波堤断面示意图Fig.6 Cross section of quarter circular breakwater

3 算例分析

以黄海平均海平面为基准面,设计高水位+1.75 m,极端高水位+2.54 m,矩形开孔沉箱防波堤顶面高程为+6 m,基床顶高程取-5.5 m,消浪室底高程-2.5 m,消浪室前墙开孔率0.3。沉箱前舱面向外海一侧开孔,沉箱为钢筋混凝土结构,箱内填石。水面以上和以下钢筋混凝土重度分别取14、24 kN/m3,水面以上和以下箱内填石重度分别取10、20 kN/m3。计算得到设计高水位、极端高水位每延米浮重G的均值分别为1 192.3、1 143.0 kN/m,稳定力矩MG的均值分别为4 486.0、4 326.7 kN·m/m,变异系数取0.05。

3.1 传统分析方法

根据波浪要素表中的波高、周期实测资料,分别计算得到2种工况下的波浪力序列PH、PV与波浪力矩序列MPH、MPV。

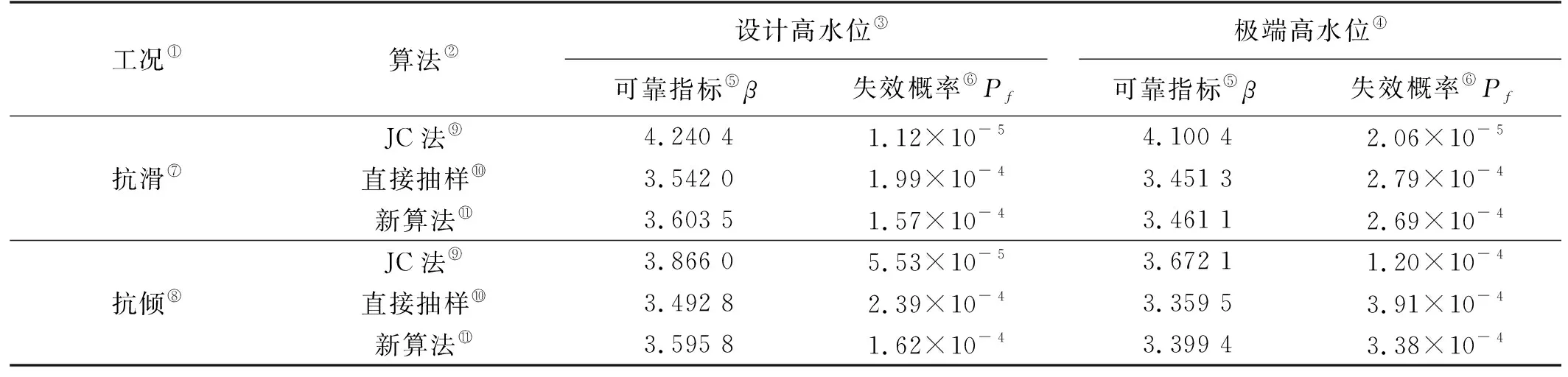
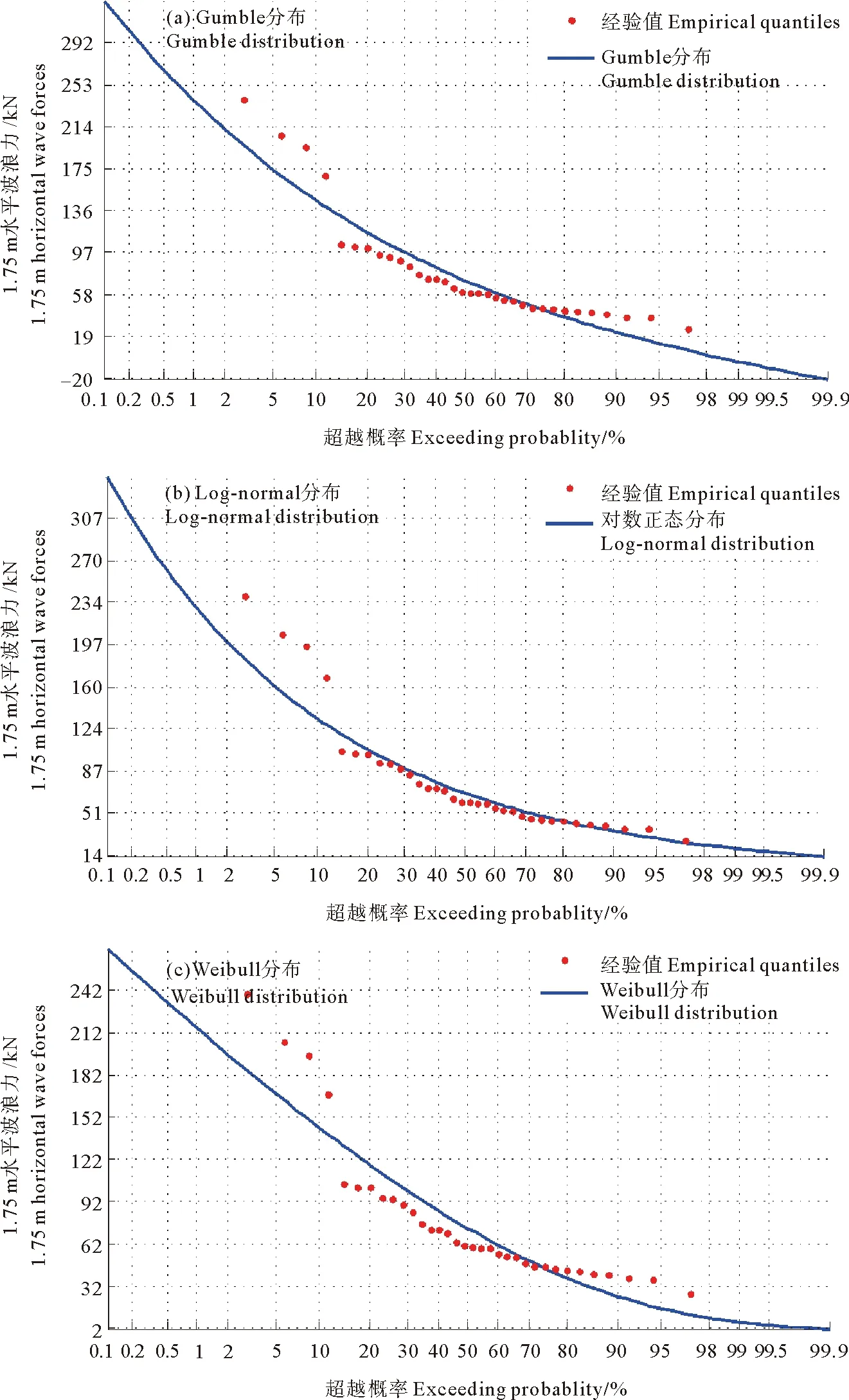
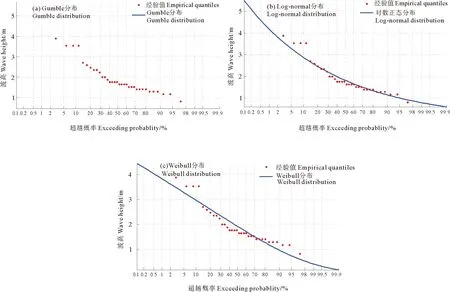
3.1.1抗滑移可靠性计算基本随机变量是水平波浪力PH、竖直波浪力PV、防波堤浮重G和摩擦系数f。分别对设计高水位和极端高水位工况下的水平波浪力和竖直波浪力序列进行处理,确定基本统计参数,如均值、标准差和相关系数(见表2)。分别采用Gumbel分布、Log-normal分布和Weibull分布曲线进行分布拟合(限于篇幅原因,本文仅列出设计高水位工况,见图7)和优度检验。各分布均通过K-S检验D

表2 波浪力统计参数Tabel 2 Statistical parameters of wave force

表4 计算结果Tabel 4 Calculation results

图7 设计高水位时水平波浪力的分布拟合图Fig.7 Distribution fitting of horizontal wave forces on the design high water level

3.1.2 抗倾覆可靠性计算同样,得知关于矩形开孔沉箱防波堤所受水平波浪力矩和竖直波浪力矩的最优分布为Log-normal分布。在变量相关的条件下,分别采用传统JC法和直接Monte Carlo模拟计算抗倾覆稳定可靠性,计算结果见表4。

3.2 新分析方法

新的防波堤可靠性分析方法只需要对连续34年实测波浪要素序列进行统计处理,确定基本统计参数(见表5),分别对波高和周期进行分布曲线拟合(限于篇幅原因,本文仅列出波高,见图8)和优度检验,均通过K-S检验(见表6),对比得到波高与周期序列的最佳分布为Gumbel分布。二者联合分布采用G-H Copula函数,通过K-S检验,D

表5 波高-周期统计参数Tabel 5 Statistical parameters of wave height and wave period

表6 波高-周期K-S检验Tabel 6 K-S Hypothetic test of wave height and wave period

图8 波高H1%分布拟合图Fig.8 Distribution fitting of wave height

3.3 计算结果

设计高水位和极端高水位2种工况条件下可靠指标对比结果:

(1)新算法计算得到的抗滑移可靠指标分别为3.603 5和3.461 1,抗倾覆可靠指标分别为3.595 8和3.399 4。

(2)传统直接抽样计算得到的抗滑移可靠指标分别为为3.542和3.451 3,同新算法相比分别相差0.061 5和0.009 8,偏差约为1.7%和0.3%;传统直接抽样法计算得到的抗倾覆可靠指标分别为3.492 8和3.359 5,同新算法相比分别相差0.103和0.039 9,偏差约为2.9%和1.2%。2种失效模式不同工况的计算结果非常接近,验证了使用新的方法分析矩形开孔沉箱防波堤的可靠性是合理有效的,计算结果是可信的。

(3)传统JC法计算得到的抗滑移可靠指标分别为4.240 4和4.100 4,同新算法相比分别相差-0.636 9和-0.639 3,偏差约为-15.0%和-15.6%;传统JC法计算得到的抗倾覆可靠指标分别为3.866 0和3.672 1,同新算法相比分别相差-0.270 2和-0.272 7,偏差约为-7.0%和-7.4%,可以发现新算法计算结果相对传统JC法保守。抗滑移可靠指标的偏差约为抗倾覆可靠指标偏差的2倍,导致这种结果出现的原因是JC法的精度是随着极限状态方程非线性程度的提高而降低的,本文中的抗滑移模式功能函数的非线性高于抗倾覆模式。