贝叶斯网络在构建学生模型中的应用综述

欧頔 曾晟

摘要：为了促进贝叶斯网络在教育领域的应用，加快实现利用贝叶斯网络为教育教学赋能的目的，文章采用文献分析法，针对贝叶斯网络在教育中的应用开展研究，通过对国内外文献的检索以及研究，筛选合适的设计实例，分析贝叶斯网络在教育中应用方向以及存在的问题，对未来的发展方向提出展望。

关键词：贝叶斯网络；人工智能；学生模型

中图分类号：TP391        文献标识码：A

文章编号：1009-3044（2023）13-0032-03

开放科学（资源服务）标识码（OSID）

1 基本概念

1.1 贝叶斯定理

贝叶斯网络也叫作信念网络，它是利用有向无环图和条件概率表来描述属性与属性间的依赖关系和联合概率分布。

联合概率分布公式如公式（1） ：

[P（x1，x2，...，xd）=i=1dP（xi∣πi）=i=1dθxi∣πi]    （1）

贝叶斯网络的训练往往以评分搜索法为基础，具体是使用评分函数（Score Function） 估测模型准确率。对于名为D的数据集合，贝叶斯网络B=的评分函数可以用下列方法计算：

[sB|D=fθ∣B∣-LLB|D]   （2）

[LL（B∣D）=i=1mlog PB（xi）] （3）

其中，[∣B∣]表示参数对象数目，[fθ]表示每个参数[θ]需要的字节，则[fθ][∣B∣]表示模型参数需要的字节数，[LL（B∣D）]表示贝叶斯网络B的对数似然，这可以体现出概率分布是比较好地描述了数据。因此，贝叶斯网络的训练等价于评分函数最小化。如果网络结构固定（名为G） ，[fθ∣B∣]为常数c。因此，将公式（4） 转换如下：

[s（B|D）=c-LL（B|D）]    （4）

如上所示，最小化评分函数转换为对参数的极大似然估计。SPSS Modeler 封装的贝叶斯网络算法可以将最大似然作为选择参数的方法[1]。

1.2 贝叶斯网络特点

贝叶斯方法可以用来计算专家系统中的不确定知识。最近几年数据库内的海量数据持续扩充，同时有研究发现，贝叶斯网络也可以用在知识发现，尤其是对于大规模数据库，贝叶斯网络更加适配，体现在：

1） 对于数据不完备的数据集，贝叶斯网络也能够处理。以往的指导性学习方法掌握一切可能的数据输入，如果某一输入的数据缺失，那么建立的模型就会有偏差，贝叶斯方法可以解决这个传统的指导性学习方法的缺点，由于贝叶斯网络反映出来的概率关系是针对整体数据域中的数据，所以在某一变量缺失的情况下，它建立的模型依然是精确的。

2） 贝叶斯网络可以根据因果关系进行学习。如果缺少了插入值，贝叶斯网络仍然能够进行决策，获得变量域的理解是数据分析的重中之重。

3） 贝叶斯网络能够促进知识和数据域的关联，因为贝叶斯统计和贝叶斯网络紧密相关。以往只有先获得处理数据域的先验知识才能建立精确预测模型，而贝叶斯网络具有因果关系，可直接进行因果先验知识的分析，通过贝叶斯网络能够获得较为全面的先验知识。

4） 贝叶斯网络能够避免数据溢出[2]。

2 贝叶斯网络概述

2.1 贝叶斯网络发展历史

贝叶斯统计的前身是英国学者贝叶斯（Bayes）在1763年发表的哲学性论文：关于概率问题求解的评论“An Essay Towards solving aproblem in the Doctrine of chances”，后来发展形成贝叶斯学派。在1921年，遗传学家SewallWright提出了一个概率模型，把有向无环图作为模型基础，认知科学和人工智能领域将其称为贝叶斯网络（Bayesain Networks，BNS）。贝叶斯网络于20世纪70年代后期取得了初步的进展。

20世纪90年代，学者们开展了进一步研究，在数据挖掘以及机器学习领域对其进行应用。最近几年，与贝叶斯学习理论相关的文章内容涉及的人工智能部分有：模式识别、聚类分析、因果推理和不确定性知识表达等。同时，ISBA作为专业研究贝叶斯理论的学术刊物网组织出现[3]。

2.2 国内外研究现状

Pearly在20 世纪 80 年代末，创造性地提出了贝叶斯网络理论[4]，并成功将其应用于专家系统。在此之后，学者们开始广泛关注贝叶斯网络，认为它是有效表示与推理不确定知识信息的工具。在理论研究和实际应用上，贝叶斯网络理论取得了很大的进展。推理、实际应用和网络学习是当前对贝叶斯网络的主要研究方向。贝叶斯网络中的学习分为两种，参数学习用于确定各个网络结点的条件概率分布。结构学习算法分为基于得分的结构学习算法与基于约束的结构学习算法。前者先以评分标准评估数据集与网络结构拟合的程度，再选取分数最高的网络结构。后者认为，贝叶斯网络可以体现随机变量之间的独立性关系。基于约束的结构学习算法首先检验训练数据集的独立性，确定各结点集之间独立性的统一条件。然后在尽可能多地覆盖这些条件的情况下，建构独立性的网络结构。Cheng[5]用互信息代替条件独立检验，把信息论应用于统计测试，提出三阶段算法等。参数学习一般通过统计样本来实现，先确定网络结构后计算其中结点的条件概率分布。常用贝叶斯参数估计、EM（期望最大化）算法、最大似然估计法和Gibbs 抽样算法。

网络推理指的是后验概率，即在给出部分证据的情况下，确定其中某些结点的取值概率。根据所要求精度的不同，将推理算法分成了近似推理算法和精確推理算法。精确推理算法常用的有连接树算法和消息传播算法。近似推理算法常用基于搜索的方法和基于 Monte Carlo 思想的采样方法。由于贝叶斯网络能够表示和推理因果关系，因此被广泛应用在包括教育领域在内的各个领域。Millan[6]用离散贝叶斯网络对学生进行测评并构建学生模型，首先，依靠贝叶斯网络预测学生回答正确的概率，据此得出一种自适应的诊断算法。Zapata[7]用贝叶斯网络建立分布式多代理教学系统，构建了学生模型，利用其推理能力建立自适用于学生的学习应用。Martin 用离散贝叶斯网络评估学生知识掌握情况，利用贝叶斯网络的推理能力预测学生掌握某一知识点的概率，并分析学习行为 [8]。王璋[9]应用离散贝叶斯网络于评估导学，预测学生掌握某一知识点的程度，说明了在评估学生方面贝叶斯网络推理机制是有效的。黄建明等人[10]把离散贝叶斯网络用于预测学生成绩的高低。学生群体掌握知识的程度是连续的，以上学者离散化连续变量的取值，将掌握程度的取值区间分割成离散值。虽然计算得到简化，但是也会损失变量特征，而且在实际情况中，区间内所有的连续值不可能都是同一种情况，这会降低预测的精度。

3 贝叶斯网络的应用

3.1 应用现状

贝叶斯网络目前主要用在以下几个方面：

1） 专家系统

贝叶斯网络的推理能力可达到专家水平，它能够模仿人的智能，解决专业领域的实际问题。如在医学上，远程医疗系统CPCSBN优于世界上常用的远程医疗诊断方法；Pathfinder用于辅助“淋巴节点”的诊断。

2） 数据挖掘

贝叶斯网络可用于辅助聚类分析。因果关系是普遍存在于客观世界的一种关系，学者们发现在数据挖掘中，贝叶斯网络能够挖掘多层、多点的因果概念关系。贝叶斯统计学作为其起源，使得含有统计性质的数据挖掘与贝叶斯网络顺理成章地结合起来。

3） 故障诊断

贝叶斯网络可用于分析故障特征，寻找故障原因；依据常见故障或当前系统状态，进行故障监控和故障预防。比如微软为帮助用户解决使用过程中可能发生的问题，在视窗软件中加入了疑难解答。

4） 学习帮助

通过引导学习者掌握事件发生的规律和事件二者的因果關系，贝叶斯推理原理可以对学习者进行学习帮助。对考试结果的研究和分析，有助于教师的思考、观点和建议。领导决策时也可以依据分析，作为自己制定工作策略的参考，指导学校的教学工作[11]。

3.2 建立学生模型

国内和国外的学者已经对学生模型做出了许多研究。一些学者从构成学生模型的内部要素角度分析建模。首都师范大学的王陆、杨卉等人[12]提出了两层动态学生模型，用广义模糊综合评判方法来评价学生的二级特征。国外部分学者[13]认为从知识水平的角度来说，对学生知识状态的主要有铅版模型、基于约束的模型、覆盖模型等。有研究者[14]总结了不同模型的特点，提出了基于覆盖模型和认知偏差或者是对其他模型的整合；还有学者[15]以学习者个性特征为关键构建学生模型，如像认知风格和认知偏好等个人特征。近年来适应性技术和情感计算不断发展，人们也开始关注基于情绪感知的学生模型。

用于自适应学习系统时，学生对节点知识的掌握程度表现为贝叶斯网络中某一节点概率[16]。节点知识分为两大类，一类为定性知识，一类为定量知识，此种图论模型就是对节点知识的结构化描述[17]。刘艳等[18]学者提出了新方法评估学生的学习情况，基于贝叶斯网络的学习评估方法可以精确地测算出学生对某块知识的掌握程度，得到学生的差异性结果，就可以开展个性化的学习策略。

建立学生模型，从信息处理的角度看就是分析处理学生学习的各种信息，包含着认知诊断和知识表示两个方面。建立模型的理论和方法有许许多多，目前常见的包括认知型、偏差型和覆盖型。覆盖型的学生模型，描述的是学习者哪些内容知道，哪些内容不知道，把学生的知识作为领域中专业知识的某个子集来描述。对于有着大量知识点的课程测试，覆盖模型能清晰地表示出先验知识。

马文龙[19]建立的适应性教学系统采用粗盖型学生模型，用一种自动和人工相结合的方法构造模型。课程的领域专家（即授课老师）先根据个人的教学经验，给出该课程某些知识点的先验概率，再由系统建立领域知识模型、构建贝叶斯网络结构、选择条件概率分布函数。系统投入使用一段时间后，已收集到足量的学生数据，可以开展推理和优化。马文龙的学习者模型模拟了知识在大脑中存储的过程。课程知识按照领域里面内在的逻辑关系被模型连接为语义网络。学习者也是以这样的逻辑顺序来学习课程知识的。所以，首先需要做的是，建立领域知识模型，即将知识点间的逻辑关系整理清楚。

对于眼下流行的教育超媒体系统，贝叶斯网络推理机制也可以有效地为其服务，如何针对其特点构造有效而准确的网络是难点重点。闫志勇[20]着眼于构造网络的过程，抓住教育超媒体系统中课程知识点与知识点关系紧密的特点，利用层次划分减少聚簇数量，在通过聚簇消除无向环方法的基础上，使得贝叶斯推理减少了计算量。

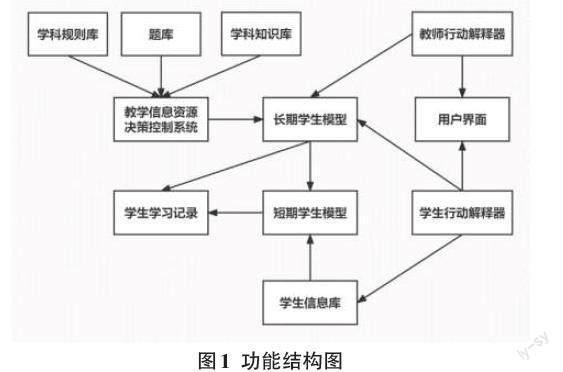
马爱利[21]设计了一个模拟系统以模拟数学的教学，以贝叶斯网为学生模型，用于远程教学，功能结构图如图1所示：

学科知识点储存在学科知识库，用于学习本科知识的所有规则储存在学科规则库。题库内是每一章节的测试题、练习题与下一章节的预习。将学科规则库、学科知识库和学生学习记录相结合，通过推理机制能够整合成教学资源，通过决策控制模型和信息控制模型能够转换为长期学生模型。学生行动解释器主要负责处理信息并针对答题情况提供反馈。教师行动解释器主要负责在学生需要帮助时给予合适的帮助，不同情况的学生会得到个性化的教学决策。学生学习记录中保存着该生题目作答情况，便于学生及教师掌握自己的学习变化[21]。

4 问题和展望

1） 在选取用于建立学生模型的学生特征时，除知识水平相关因素外，也应考虑个性特征。如学习风格、学习兴趣、认知偏好等。未来的研究中，可以对学生特征的建模进行补充，扩充学生模型。

2） 领域专家提供的知识点关系较为主观，贝叶斯网络具备学习能力，如若提供足够的实验数据，贝叶斯网络完全可以自动构建网络结构，模型的完备性和准确性会大幅提升。未来的研究中，可以利用贝叶斯网络的学习算法进行知识地图的分析和构建。

3） 当前在设计个性化学习路径时，更为关注的是对学习者知识掌握程度的预测，未来的研究应更多地结合学生的学习风格、认知偏好等因素，以推荐更加个性化的学习路径。

参考文献：

[1] 毛瑶瑶.数据挖掘模型在智慧教育中的应用研究[D].西安：西安电子科技大学，2021.

[2] 王玮，陈恩红，王煦法.基于贝叶斯方法的知识发现[J].小型微型计算机系统，2000，21（7）：703-705.

[3] 慕春棣，戴剑彬，叶俊，等.用于数据挖掘的贝叶斯网络[J].软件学报，2000，11（5）：660-666.

[4] A Bayesian Diagnostic Algorithm for Student [M]. San Francisco： Morgan Kaufmann， 1988：51-53.

[5] Cheng J， Grainer  J. Kelly. How To Build an Effective Knowledge Map [J]. Artificial Intelligence，2002（137）：43-90.

[6] Learning Bayesian Networks The Combination of [J]. User Modeling and User-Adapted Interaction， 2002，12（2-3）：281-330 .

[7] Zapata-Rivera J D，Greer J.Inspectable Bayesian student modelling servers in multi-agent tutoring systems[J].International Journal of Human-Computer Studies，2004，61（4）：535-563.

[8] Cristina Conati，Abigail Gertner，Kurt Vanlehn.Using bayesian networks to manage uncertainty in student modeling[J]. International Journal of  Human-Computer Studies，1995，42（6）：575-591.

[9] 王璋.基于贝叶斯网络的评估导学方法研究[D].杭州：浙江工业大学，2006.

[10] 黄建明.贝叶斯网络在学生成绩预测中的应用[J].计算机科学，2012，39（S3）：280-282.

[11] 沈海峰.基于贝叶斯网络数据挖掘技术理论及算法的研究[D].合肥：合肥工业大学，2002.

[12] 杨卉，王陆，冯红.在智能教学系统中两层动态学生模型的研究[J].电化教育研究，2005（1）：72-75.

[13] 陈仕品，张剑平.适应性学习支持系统的学生模型研究[J].中国电化教育，2010（5）：112-117.

[14] 孙中红.个性化智能网络教学系统中学生模型的研究[J].中国电化教育，2009（10）：107-110.

[15] 刘小丹，胡小红.自适应学习系统中基于情绪感知的学生模型设计[J].中国教育信息化·高教职教，2015（10）：85-88.

[16] 董晓辉，杨晓宏，张学军.自适应学习技术研究現状与展望[J].电化教育研究，2017，38（2）：91-97，121.

[17] 陈丽花.贝叶斯网络在学生模型建模中的应用分析[J].微型机与应用，2010，29（8）：80-82.

[18] 刘艳，张锐.基于贝叶斯网络的学习评估模型及其在E-learning系统的应用[J].滁州学院学报，2009，11（4）：49-52，55.

[19] 马文龙，瞿有甜，张金伟.贝叶斯网络在适应性教学系统中的应用研究[J].计算机系统应用，2008，17（1）：68-71.

[20] 闫志勇，李明，倪劲峰，等.贝叶斯网络在自适应教育超媒体中的应用[J].计算机工程与应用，2002，38（8）：217-219.

[21] 马爱利，张卓奎.贝叶斯网络在远程教学中的应用[J].现代电子技术，2008，31（2）：129-133.

【通联编辑：唐一东】