一种自动聚类的离群点识别方法研究

黄强 叶青 聂斌 朱彦陈 郭永坤

摘  要：针对传统离群点识别方法对数据的分布形状和密度有特定要求，需设定参数的问题，提出了一种自动聚类的离群点识别方法。该方法通过引入相互K近邻数来表示数据对象的离群度，对数据的分布形状、分布密度无要求，可以输出全局离群点、局部离群点和离群簇；通过k次迭代来实现自动聚类，无需人为设定参数。通过合成数据以及UCI数据实验，验证了该方法的有效性、普适性。

关键词：局部离群点；离群点识别；离群簇；自动聚类；数据挖掘

中图分类号：TP301    文献标识码：A  文章编号：2096-4706（2023）07-0006-05

Abstract： Aiming at the problem that traditional outlier recognition methods have specific requirements for the distribution shape and distribution density of data and need to set parameters， an automatic clustering outlier recognition method is proposed. This method represents the outlier degree of data objects by introducing the mutual K-nearest neighbor number， with no requiring for the distribution shape and distribution density of the data， and can output global outliers， local outliers， and outlier cluster; Automatic clustering is achieved through k iterations， no need to manually set parameters. The effectiveness and universality of this method are verified through synthetic data and UCI data experiments.

Keywords： local outlier; outlier recognition; outlier cluster; automatic clustering; data mining

0  引  言

隨着信息技术和数据密集型科学的发展，离群点识别在很多领域得到研究和应用，比如医疗领域、污水站点监测、图像异常检测、网络入侵检测等[1-4]。

离群点是指与数据集中其他数据对象显著偏离，像是产生于不同机制的数据对象[5]。离群点的类型有全局离群点、局部离群点和集体离群点，离群点识别方法可以大致分为基于统计的、基于距离的、基于密度的、基于聚类的四大类[6]。

基于统计的方法[7]假设数据服从某一分布，将不符合该分布特征的数据视为离群点。此类方法常用于数据分布已知的数据集[8]，但实际中的数据分布难以预知，也并非由单一分布组成。基于距离的离群点定义最早是由Knorr和Ng[9]提出的，由于算法思想简单易懂、识别效果较好被广泛地研究和应用。基于距离的方法中的参数是基于全局的参数，没有考虑到数据对象局部情况的不同，导致不能识别出局部离群点；且识别效果对参数敏感，不同的参数会有不同的识别效果。基于密度的方法[10-12]使用密度描述数据对象邻域的疏密，能很好地识别出局部离群点，缺点是识别效果对算法参数敏感。

以上方法考虑了只存在单个离群点的情况，不适用于存在离群簇（集体离群点）的数据。基于聚类的方法[13-16]可以识别出数据中的离群簇，该类方法的思想是对数据进行聚类，不属于任何类别的数据对象以及小类别内的所有数据对象被划分为离群数据。如何区分大类和小类是一个问题，此外部分基于聚类的识别方法对参数敏感。

基于此，本文提出了一种自动聚类的离群点识别方法（Outlier Recognition Method Using Automatic Clustering， ORMUAC），该方法通过聚类自动的输出离群点和离群簇，对数据对象的分布形状和密度无要求，无需人为设定参数。ORMUAC使用相互K近邻数衡量数据对象的离群度，数据对象的相互K近邻数越少就越可能是离群点。相互K近邻是一个非全局的参数，因此也可用于识别局部离群点。

1  自动聚类的离群点识别方法

传统离群点识别方法大都缺乏普适性，有些方法对数据的分布形状或者密度分布有特定要求，无法识别出离群簇或者局部离群点；有些方法需要人为设定参数，增加了算法的使用难度。基于此，本文提出了具有普适性的ORMUAC方法，该方法对数据的分布形状和密度无要求，无需人为设定参数。在详细介绍该算法前先阐述一些相关理论概念。

1.1  相关概念

K近邻：数据集d中，距离数据对象o最近的k个数据对象组成的集合称为数据对象o的K近邻，表示为：

Nk={ p|d（o， p）≤dk（o），p≠o}                 （1）

其中，d（o， p）表示数据对象o和p之间的距离，dk（o）表示距离数据对象o第k近邻的数据对象与数据对象o之间的距离。

相互K近邻：当数据对象p属于数据对象o的K近邻，同时数据对象o属于数据对象p的K近邻时，数据对象p和数据对象o是相互K近邻。表示为：

MN（o）={ p| p∈Nk （o），o∈Nk（ p）}                （2）

近邻链接点：如果数据对象o的相互K近邻个数不为零，那么数据对象o就称作近邻链接点。

基于相互K近邻的离群点：如果数据对象o的相互K近邻的个数为零，那么数据对象o被称为基于相互K近邻的离群点。

α离群簇：在数据完成聚类后，如果类内数据对象的个数小于阈值α，则组成该类的全部数据对象被称为α离群簇。

文献[17]中提到一个六度分离理论，该理论阐述为：任何两个陌生人之间只要通过6个人就可以相互认识。在Facebook的一篇报告[18]中这个数字变成了4.74（数据范围为全球），当把范围缩小到一个国家时，人们之间的间隔度只有3度。这表明个体间存在一个间隔度值，当人能直接或间接认识到的人数小于这个值就无法认识更多的人，从而被隔离成为小众。类比聚类，当某一数据对象的相互K近邻个数小于阈值α时，这些数据对象就不能被划到大类，变成离群簇。阈值α不是固定的，不同的数据环境有着不同的α值。

α值的确定：当自动聚类完成后，输出的K值就是判别某一类是否为α离群簇的阈值α，如果类的数据对象个数小于α，将该类输出为α离群簇。

当数据聚类的类别不再发生变化时，所有的数据对象都被正确归类，数据聚类达到稳定状态；这时对应的k值就是该数据集的间隔度α。

1.2  算法原理与步骤

ORMUAC是通过近邻链接点将相似的数据归为一类，在所有数据被归类之后，单独成一类的数据对象被输出为离群点，类内数据个数小于阈值α的小类则被输出为α离群簇。ORMUAC算法流程分为两部分，第一部分是自动聚类和输出离群点，第二部分是输出为α离群簇。

第一部分：从数据集D中随机选择一个数据对象o，判断该数据对象是否为近邻链接点。若不是，标记为离群点；否则，将数据对象o及其相互K近邻标记为一类。接着遍历数据对象o的相互K近鄰，如果数据对象o的相互K近邻也为近邻链接点，继续递归访问该近邻链接点的相互K近

邻；循环这一步骤，直到遍历完所有近邻链接点及其相互K近邻，完成一次归类。以同样的方式继续访问数据集D中的下个未被访问的数据对象，直至遍历完数据集D中所有数据。

该如何给出合适相互K近邻值。通过实验发现小样本数据集的k值一般低于25，本文采用迭代的方式找到合适的k值。k值从2到25迭代（实验结果表明实际迭代次数平均约为12次，远低于25次），当相邻两次的聚类输出类别数相等时停止迭代，此时k值为最佳K近邻值。迭代时会频繁地计算数据对象的相互K近邻，为减少开销采用KD树来存储相互K近邻。聚类前先扫描一遍数据集，建立25—近邻KD树，后续迭代时直接查找KD树即可找出数据对象的任意K近邻。自动聚类的步骤见算法1。

算法1：Auto-Clustering（D）

输入：数据集D

输出：聚类结果C=（C1，C2，…，Cn），k

1）初始化：I0=0，k=2，n=0。

2）扫描数据集D，将每个数据的25-近邻数存储到KD树。

3）从数据集D中选取一个未被访问的数据对象O。

4）通过查找KD树，判断O是否为近邻链接点；若是，n=n+1，Cn=Cn∪MN（O）∪O，visited（O）=true，否则，输出为离群点。

5）如果?P∈Cn并且visited（P）≠true，Cn=Cn∪MN（P），visited（P）=true，直到遍历完Cn中所有未被访问数据。

6）如果数据集D还有未被访问的数据，跳到步骤3）。

7）当数据集D中数据全部遍历完毕，将类别个数n赋值给Ik。

8）如果Ik≠Ik-1，k=k+1，将数据集D中数据的visited值设为false，跳到步骤3），否则，结束程序。

9）End。

第二部分：聚类完成之后，数据都被全部归类，数据对象的间隔度α随之确定，根据最终聚类结果确定并输出α离群簇。ORMUAC具体步骤见算法2。

算法2：ORMUAC（D）

输入：数据集D

输出：离群点，离群簇

1）执行Auto-Clustering（D），输出聚类结果C=C=（C1，

C2，…，Cn）、近邻值k、离群点。

2）令α=k，如果|Ci|≤α，（i=1，2，…，n），将Ci输出为离群簇。

3）End。

ORMUAC识别过程如图1所示，相互K近邻的k从2开始迭代聚类，k=2时聚类输出类别数为8，k=3时输出类别数为5，与k为4时的输出类别数一致；此时聚类数目不再随k增加而变化，即聚类达到稳定状态。这意味着相互K近邻k=3时的聚类结果为最佳输出，将此时k值（k=3）赋予α，由于A类数据样本数小于α，簇A被输出为α离群簇，点p单独成一类被输出为离群点。

1.3  算法复杂度分析

Auto-clustering算法通过KD树来寻找数据对象的K近邻，时间复杂度为O（N logN），遍历数据集的时间复杂度为O（N），Auto-clustering的时间复杂度为O（N logN）+O（N）；ORMUAC在寻找最佳k值时需要迭代Auto-clustering算法k次，因此ORMUAC的时间复杂度为O（N logN）。

KD树的空间复杂度为O（N），用于存储类标记的数组长度为N，存储相互K近邻所占的空间长度小于KN，所以ORMUAC算法的空间复杂度为O（N）。

2  实验与分析

实验部分将根据合成数据、真实数据的实验结果来评估ORMUAC算法的性能，同时将K-means[13]和DBSCAN[14]两种经典算法作为对照算法。采用召回率（R）、精确率（P）以及精确率和召回率的调和均值（F）作为衡量指标。评价指标R、P以及F的值域为[0，1]，数值越大实验效果越好。

2.1  K值与样本量关系实验

根據UCI数据的k值实验结果，图2绘制了相互K近邻值与数据集样本量的关系图。从图中可以看出二者关系是非线性的，相互近邻数k值随着数据样本量波动增加，k在样本量为6 000时达到最大值24，随后再减少。

虽然ORMUAC采用迭代方式来给出最佳k值，但迭代次数k较小；实验结果表明当样本量较小时，实际迭代次数平均约为12次，远低于25次，不会造成算法时间复杂度的突增。另外，实际操作时k不用从2开始迭代，可根据样本量设置合适初始k值以减少迭代次数。

2.2  合成数据实验

为验证ORMUAC可行性和有效性，采用合成数据集进行对比实验。3个数据集均为二维数据集，D1有4个类别，共118个数据，包含9个离群数据；D2只有一个类别，共有108个数据，其中含有8个离群数据；D3共有3个类别，共有357个数据，其中包含10个离群点，数据信息如表1所示。

为模拟真实数据情况和保证实验的科学性，三种合成数据集的密度分布有均匀和不均匀的，形状分布有球状和非球状的，数据类别有单类别和多类别的；各自都包含局部离群点、全局离群点以及离群簇。数据分布情况如图3所示，空心点为离群数据，实心点为正常数据。

实验过程中，K-means需要给定类别个数k、距离阈值d两个参数，DBSCAN算法中需要给定距离阈值d和最少数据个数P两个参数。实验中设定的参数值均为使得两种对比算法识别效果达到最佳时的参数值。

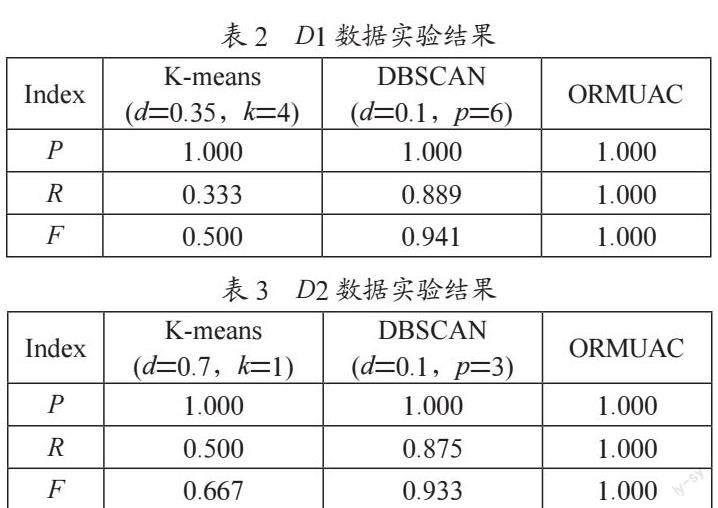
表2、表3和表4记录了三种算法的合成数据实验的实验结果，从合成数据实验结果可以知道：

1）D1数据集实验中，DBSCAN识别效果较好，F值为0.941略低于ORMUAC；D1数据集中多数离群数据分布在中心位置导致K-means的识别结果最差，虽然p值为1，但F值却低至0.5；ORMUAC表现最好，各项指标均为最高。

2）在单类别、多密度和包含环内离群点的D2数据集实验中，因环形数据和分布中间数据的密度不同，导致DBSCAN的F值稍有降低为0.941。K-means根据数据对象距离质心的远近来判断数据是否为离群点，因而其在环形分布的D2中效果很不理想，F值仅为0.667；ORMUAC表现依旧最好。

3）对于分布非球状、密度不均匀的D3数据集，DBSCAN的识别效果不佳，调和均值F仅为0.886；K-means虽然p值很高但调和均值仅为0.181，召回率R值低至0.1，意味其遗漏了大部分的离群点。RORMUAC则依然识别出了数据集中全部离群数据。

合成数据实验表明：相较于对比算法ORMUAC能有效应用于分布多样、密度不均的数据集，具有更好的普适性。

2.3  真实数据实验

为进一步验证ORMUAC的有效性，选取来自UCI数据库[19]的三组真实数据集，Iris、banknote authentication和Breast Cancer Wisconsin数据集的wdbc数据进行进一步对比实验，数据信息详如表5所示。

为更好地完成实验，参照文献[20，21]对数据集做了以下处理：Iris有三个类别，每类50个数据样本；将其中一类全部50个数据对象作为正常点，从剩下两类中各取5个数据对象作为离群点，构成第一组实验数据（Iris）。banknote authentication有两个类别，各自包含762和610个样本；大类作为正常类别，再从小类中随机取20个数据对象作为离群点，组成第二组实验数据（Banknote）。wdbc有B和M两个类别，各自包含357和212个数据样本；将B类当作正常类别，再从M类中随机取10个数据对象作为离群点，以此作为第三组实验数据（wdbc）。

实验结果如表6、7、8和图4所示，实验分析具体为：

1）Iris数据集实验中，三种算法识别效果都还不错，ORMUAC和DBSCAN表现一致，二者综合指标F值均为0.953，K-means表现其次，综合指标F值为0.909。

2）ORMUAC在Banknote数据实验表现要优于另外两种算法，其中P和R两者指标值都要高于另外两种算法，并且F值相对最高为0.869。

3）高维数据wdbc对比实验中，K-means和DBSCAN的识别效果一致，指标P、R、F值分别为0.700、0.636和0.667，ORMUAC的表现依旧最好，P值、R值和F值为0.800、0.667、0.761均高于两种对比算法。

真实数据实验证明：相较对比算法ORMUAC识别准确率高有更好的识别效果，能够更有效地应用于真实数据集。

为验证ORMUAC的普适性和有效性，采用合成数据集和真实数据集做了验证实验。合成数据实验中，ORMUAC能够很好地适应分布形状不规则、密度分布不均匀的数据，验证了ORMUAC的普适性。真实数据实验中ORMUAC的表现最佳，P、R和F值均为三种算法之中最高，进一步证明了ORMUAC的普适性和有效性。

图4  真实数据实验结果

3  结  论

本文提出了一种自动聚类的离群点识别方法，该方法可自动识别出数据集中的全局离群点、局部离群点以及离群簇，且对数据的分布形状、密度无要求，有着较强的普适性。理论分析与对比实验证明了新方法能更有效应用于分布复杂且离群类型多样的数据集。

接下来的研究可从优化新算法在高维、大数据集中的效率方面着手。

参考文献：

[1] BRZEZI?SKA A N，HORY? C. Outliers in Covid 19 data based on Rule representation-the analysis of LOF algorithm [J].Procedia Computer Science，2021，192：3010-3019.

[2] 吕承侃，沈飞，张正涛，等.图像异常检测研究现状综述 [J].自动化学报，2022，48（6）：1402-1428.

[3] MOHAMMADPOUR L，LING T C，LIEW C S，et al. A Survey of CNN-Based Network Intrusion Detection [J].Applied Sciences，2022，12（16）：8162-8162.

[4] 黄彦斌，骆德汉，蔡高琰.基于电力数据分析的污水站点监测方法研究 [J].现代信息科技，2021，5（21）：121-125.

[5] HAWKINS D. Identification of outliers [M].London：Chapman and Hall，1980.

[6] 周玉，朱文豪，房倩，等.基于聚类的离群点检测方法研究综述 [J].计算机工程与应用，2021，57（12）：37-45.

[7] 黄旺华，王钦若.基于距离统计的有序纹理点云离群点检测 [J].计算技术与自动化，2019，38（1）：139-144.

[8] 梅林，张凤荔，高强.离群点检测技术综述 [J].计算机应用研究，2020，37（12）：3521-3527.

[9] KNORR E M，NG R T. Algorithms for Mining Distance-Based Outliers in Large Datasets [C]//Proceedings of the 24rd International Conference on Very Large Data Bases.San Francisco：Morgan Kaufmann Publishers Inc，1998：392-403.

[10] BREUNIG M M，KRIEGEL H P，NG R T，et al. LOF：Identifying Density-Based Local Outliers [EB/OL].[2022-10-28].https：//www.docin.com/p-291134797.html.

[11] HA J，SEOK S，LEE J S. Robust outlier detection using the instability factor [J].Knowledge-Based Systems，2014，63：15-23.

[12] SHAO M L，QI D Y，XUE H L. Big data outlier detection model based on improved density peak algorithm [J].Journal of Intelligent & Fuzzy Systems，2021，40（4）：6185-6194.

[13] 杨俊闯，赵超.K-Means聚类算法研究综述 [J].计算机工程与应用，2019，55（23）：7-14+63.

[14] ESTER M，KRIEGEL H P，SANDER J，et al. A density-based algorithm for discovering clusters in large spatial data bases with noise [C]//Proceedings of the 2nd International Conference on Knowledge Discovering in Databases and Data Mining （KDD-96）.Massachusetts：AAAI Press，1996，226-232.

[15] GAN G J，NG M K P. K-means clustering with outlier removal [J].Pattern Recognition Letters，2017，90：8-14.

[16] HUANG J L，ZHU Q S，YANG L J，et al. A Novel Outlier Cluster Detection Algorithm without Top-n Parameter [J].Knowledge-Based Systems，2017，121：32-40.

[17] KERBY M，KERBY M. Six degrees of separation [J].AOPA pilot，2012，55（2），68-68.

[18] BACKSTROM L，BOLDI P，ROSA M，et al. Four Degrees of Separation [EB/OL].[2022-10-28].http：//snap.stanford.edu/class/cs224w-readings/backstrom12four.pdf.

[19] DUA D，GRAFF C. UCI Machine Learning Repository [EB/OL].[2022-10-28].http：//archive.ics.uci.edu/ml.

[20] HAWKIN S，HE H X，WILLIAMS G J，et al．Outlier Detection Using Replicator Neural NetworKs [C]//2000：Data Warehousing and Knowledge Discovery.France：Springer，2002：4-6.

[21] ZHU Q S，FAN X G，FENG J. Outlier detection based on K_Neighborhood MST [C]//2014 IEEE 15th International Conferenceon Information Reuse and Integration.Redwood City：IEEE，2014，718-724.

作者簡介：黄强（1993—），男，汉族，江西上饶人，助教，硕士，主要研究方向：数据挖掘、中医信息学研究。