一种融合逻辑回归的麻雀搜索算法研究

彭一凯 蒲红平

摘  要：为了改善麻雀搜索算法收敛速度缓慢、局部搜索能力较弱等问题，提出了一种融合逻辑回归的麻雀搜索算法。文章通过引入Sine-Sine混沌、逻辑回归模型、步长因子组合策略来改进麻雀搜索算法的不足之处。实验结果表明该算法具有更好的收敛速度、寻优精度和稳定性的能力。同时，利用该算法预估Taylor定位算法的初始值，解决了TayLor的初值难以选择问题，进一步验证了改进策略的有效性。

关键词：麻雀搜索算法；Sine-Sine混沌；逻辑回归模型；步长因子

中图分类号：TP18  文獻标识码：A  文章编号：2096-4706（2023）08-0001-07

Abstract： In order to improve the slow convergence speed and weak local search ability of Sparrow Search Algorithm， a Sparrow Search Algorithm incorporating Logic Regression is proposed. This paper improves the shortcomings of the Sparrow Search Algorithm by introducing Sine-Sine chaos， Logical Regression model and step factor combination strategy. The experimental results show that the algorithm has better convergence speed， optimization accuracy and stability. At the same time， the algorithm is used to estimate the initial value of Taylor location algorithm， which solves the problem that it is difficult to select the initial value of TayLor， and further verifies the effectiveness of the improved strategy.

Keywords： Sparrow Search Algorithm; Sine-Sine chaos; Logistic Regression model; step factor

0  引  言

针对不同的优化问题，众多学者提出了相关算法以及改进算法[1-4]。尤其，近年来群体智能优化算法的效果被大众所认知，进而越来越多新的群体智能算法被提出，如蝴蝶优化算法（Butterfly Optimization Algorithm， BOA）[5]、蝗虫优化算法（Grasshopper optimization algorithm， GOA）[6]、麻雀搜索算法（Sparrow search algorithm， SSA）[7]等。智能优化算法综述[8]对近年6种算法进行基准测试函数试验并分析，它的结论表明SSA在优化问题的求解精度、收敛速度、执行时间等方面具有极好的效果。

SSA的寻优过程分为探索和开发两个阶段。探索阶段是以随机性方式进行全局搜索，进而达到解空间的区域划分。开发阶段是对探索阶段的划分区域进行更精细的局部搜索，从而获得更高精度的解。从两个过程中不难发现，探索阶段容易导致解的精度下降及收敛速度降低，而开发阶段又易使解陷入局部最优。

针对上述问题，吕鑫等[9]通过Tent混沌映射、高斯变异和Tent混沌扰动等方式来克服算法易陷入局部极值点的缺陷。欧阳城添等[10]通过折射反向学习、疯狂算子等方式来寻找高质量的解。文献[11]引入可变螺旋因子减少越界个体的数量，保证算法细致灵活的搜索能力，同时以逐维镜像学习策略来克服算法易陷局部极值点的缺点。这些改进措施在一定程度上提高了算法的寻优能力，但依然有不足之处，例如Tent混沌遍历性较弱；疯狂算子和逐维镜像学习易导致有效解的丢失。因此，本文提出一种融合回归模型的麻雀搜索算法（Sparrow search algorithm with logistic regression， SSAWLR），首先通过朱明豪[12]提到的Sine-Sine混沌（SSM）映射初始化种群，使得初代麻雀个体具有更高的随机性及遍历性；再用Logit模型自适应调整发现者和跟随者的数量，进而更加灵活的平衡探索和开发两个阶段；同时引入步长因子增加发现者的跳跃步长，增加算法高精度解的搜索能力。最后，选取粒子群算法（PSO）[13]、鲸鱼优化算法（WOA）[14]、灰狼优化算法（GWO）[15]、SSA四种算法在15个常用基准测试函数进行仿真试验，并将SSAWLR用于Taylor迭代初值的估计问题[16]，验证了本文算法的可行性和有效性。

1  SSA

SSA是通过模拟麻雀觅食行为和反捕食行而抽象出来的一种群体智能优化算法。其仿生原理是：用搜索空间中的点模拟自然界中的麻雀个体，将搜索优化过程模拟成麻雀觅食和反捕食的过程，将所求问题的适应度函数值度量成麻雀种群个体携带的能量高低，将保留高能量个体过程类比为搜索和优化过程中保留最优可行解的过程。

麻雀个体在搜索空间的位置信息可用矩阵，其中 表示第i只麻雀的m维位置信息，则它们对应的适应度函数为 。

麻雀搜索算法中的种群以不同工作机制搜索最优解，并根据不同机制分别划分为发现者、跟随者、预警者。发现者为种群提供搜索方向，跟随者为种群提供精细搜索，预警者为种群增加跳出局部最优能力。发现者占种群总数的10%～20%，其位置更新公式为：

式（1）中：t表示当前迭代次数；T表示最大的迭代次数；α表示（0，1]的均匀随机数；Q表示服从标准正态分布的随机数；L表示大小为1×d且元素均为1的矩阵；R表示[0，1]的一个随机数，即警戒值；ST表示[0.5，1]的一个自选安全值。当R＜ST时，表明周围无捕食者，发现者能对该区域更精细化搜索。当R＞ST时，表明发现捕食者，发现者会带领种群前往更安全的区域。

跟随者占剩余种群的数量，其位置更新公式为：

式（2）中：xp表示当前发现者占据的最优位置；xworst是当前全局最差位置。A表示一个只含有1或-1元素的1×d维矩阵，其中A+=AT（AAT）-1。n表示种群数量，当i＞n/2时，跟随者没有获取食物需要自己寻找食物获取能量；当i≤n/2，跟随者追寻发现者的方向与之争夺更高能量的食物。

预警者从整个种群中随机挑选，占群体总数的10%～20%，其位置更新公式为：

式（3）中： 表示当前全局最优位置。β表示控制步长的参数，它是服从均值为0，方差为1的正态分布随机数。K表示属于[-1，1]的随机数，它控制着麻雀运动的方向以及步长。ε是一个避免分母为0的极小值。fi、fg、fw分别表示当前第i只麻雀个体的适应度值、麻雀个体中最优适应度值以及麻雀个体中最差适应度值。

2  SSAWLR

2.1  Sine-Sine混沌映射

智能优化算法原理是通过迭代更新初始种群的方式逼近目标函数的解，所以算法寻优效果的好坏与初始种群是否均匀密不可分。在SSA中，采用随机方式映射种群，这容易造成种群分布不均的情景。相比随机映射来说，混沌映射具有遍历性、随机性、普适性等特点，且它是一种在有限区域内永不重复的映射。所以，通过混沌映射得到的初代种群，不仅能拥有丰富的多样性，还能提高算法的全局寻优性能。

典型的混沌模型有Logistic映射和Tent映射等，而它们不仅稳定性先天不足，且中间和两边密度分布不均匀的缺陷。SSM是具有鲁棒性的特殊映射，该映射具有分布均匀和稳定性好等优点。SSM映射的数学表达式为：

yn+1=（u·sin（π·c1·yn）+（1-u）·sin（π·c2·yn））mod1   u∈[0，1]（4）

其中，u是整个系统的参数，本文取值为0.75。ci（i={1，2}）是系统的控制参数，分别取值50.96和50.32。mod是取余数。

本文采用SSM映射SSA的初始种群。由式（4）可得，SSAWLR的初始种群公式为：

xi，d=xl+（xu-xl）·yi，d                           （5）

其中：xl、xu分别表示搜索范围的下限以及上限，yi，d由式（5）产生的混沌值。

Logistic映射、Tent映射和SSM映射分别进行1 000次迭代运算，结果如图1所示。Logistic函数迭代結果呈现为明显的凹槽分布，其初始种群极易分布在上下界周围。Tent函数迭代结果分布较为均匀，但两头的选取次数依然较高，初始种群均匀性较差，易导致初代种群聚集在边界，影响寻优性能。而SSM函数迭代结果分布更加均匀，优于前两种映射迭代结果。

2.2  Logit模型

SSA中的发现者和跟随者的数量是固定不变的，其中发现者的职责是指明种群前进的方向，但到后期并不能提高寻优精度，而跟随者是依据发现者的方向进行局部搜索，前期更多的跟随者反而会使全局搜索能力下降。针对这种情景，可以采用动态调整策略来改变它们各自的数量。Logit模型曲线具有两头较平缓，中间陡峭的特点，这能满足算法迭代前期发现者数量多且缓慢下降，后期发现者数量少的需求，因此本文借鉴了该模型曲线。动态调整策略的公式为：

式（6）中：k1、k2表示控制参数，分别控制P的取值上限以及取值下限；t为当前迭代次数；tmax是最大迭代次数。在本文中取值k1=1，k2=0.1。

针对动态调整公式的仿真如图2所示。由图可知，前期发现者在麻雀总数中占比高，中期发现者数量陡降，后期发现者占比小且稳定。

2.3  步长因子

针对麻雀搜索算法的发现者的位置更新公式（见式（1））中的  进行迭代仿真。假设种群规模为30，迭代次数为200次。仿真结果如图3所示。

从仿真结果可得，指数项高密度区间是[0.8，1]，这导致发现者的移动步长较短，影响了算法收敛速度。因此，针对此问题，在原有公式基础上增加了步长因子λ。改进的发现者位置更新公式为：

针对改进后的发现者位置更新公式（如式（7）所示）中的  进行迭代仿真。假设条件相同，仿真结果如图4所示。由图可知，改进后的指数项密度区间为[0.6，1]，更宽的密度区间有利于搜索空间更均匀划分，加强了算法局部开发能力。

2.4  越界处理方式

越界处理通常有2种方式：1）边界值替换越界值；2）随机回归值替换越界值。方式1）会导致解容易聚集于边界，降低了寻优效率以及精度。方式2）虽然解决了边界聚集问题，但也丢失了麻雀个体位置更新的趋势。为了解决两种方式的各自缺陷，本文将两种方法进行结合，越界处理公式为：

式（9）中：h是一个[0，1]区间的随机数。该方法既能让部分越界值的回归具有一定的弹性，还能使得其他越界值保留位置更新趋势，提升了麻雀个体的多样性。

2.5  算法流程

算法流程图如图5所示。

2.6  时间复杂度分析

时间复杂度是衡量算法性能的重要指标，能直观表达算法的运算时间。

假设原算法的种群规模为P，最大迭代次数为N，维数为D，那么原算法的时间复杂度为O（P·N·D）。从宏观上看，改进后的麻雀算法并没有改变算法的本身结构和循环过程，所以它的时间复杂度也是O（P·N·D），与原算法时间复杂度一致。从微观上看，混沌映射增加了初始种群时算法的复杂度，Logit模型以及步长因子增加了发现者的算法复杂度，但这些改进策略的引入并没有增加算法的数量级，所以时间复杂度还是O（P·N·D）。

3  算法性能测试

3.1  实验设计

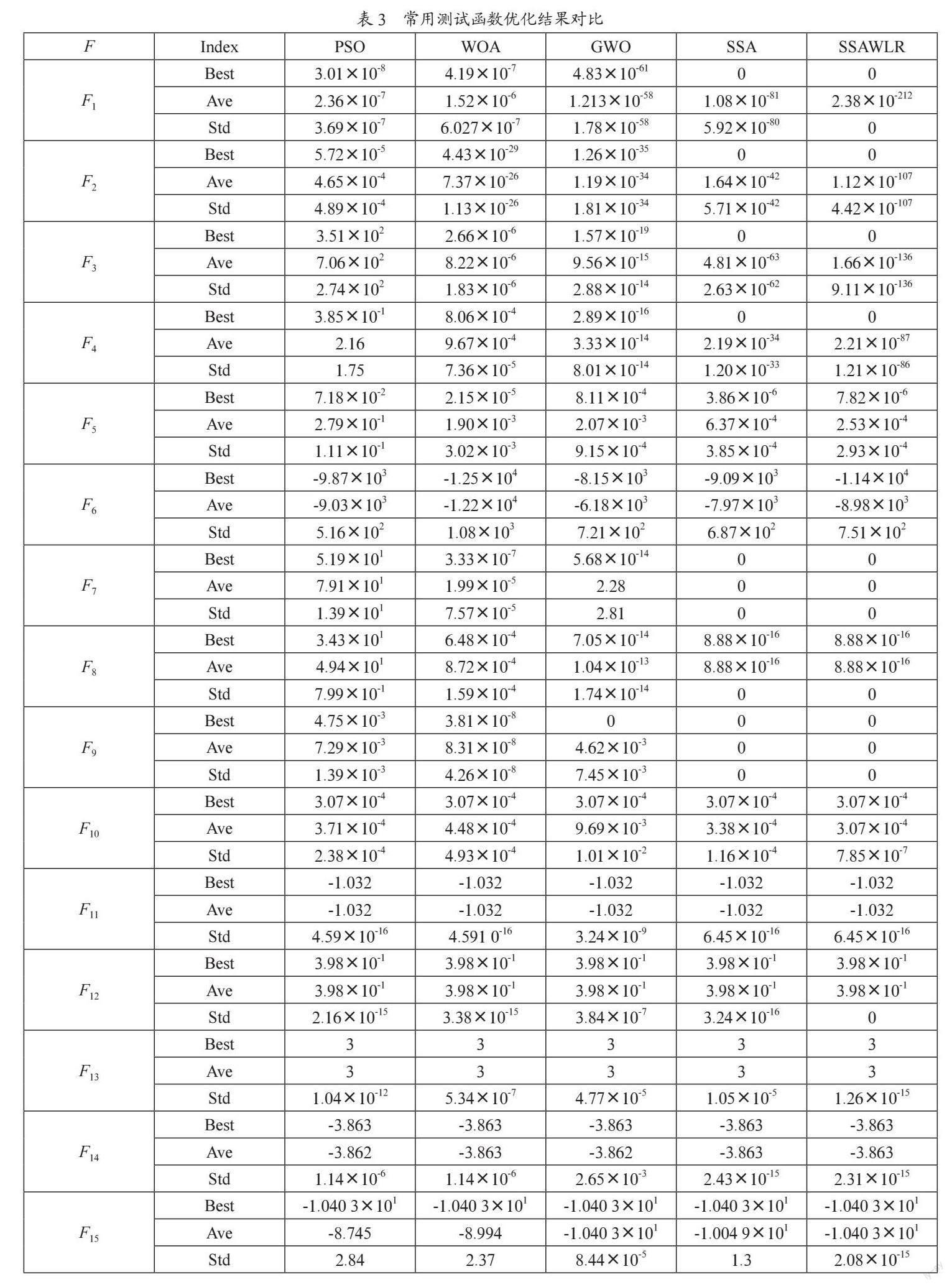
为了验证SSAWLR的性能及可行性，本文选取PSO、GWO、WOA、SSA四种算法在15个常用的基本测试函数进行对比测试。算法参数在表1中列出，15个测试函数在表2中列出，其中F1～F5的单峰值函数测试算法的精度以及收敛能力，F6～F9的多峰值函数和F10～F15的固定维函数能测试算法跳出局部极值点的能力。每个算法的种群规模和最大迭代次数分别为30和1 000，为了避免偶然因素影响，每个算法分别独立运行30次计算其最佳值（best）、平均值（Ave）、标准值（Std），每个指标的最优值以粗体处理，最后进行实验结果分析。

3.2  算法性能对比分析

由表3可知，SSAWLR在大部分函数中排名第一，尤其在函数F7、F9、F12、F14、F15中不仅寻到了理论最优值而且其方差最小，可见SSAWLR具备很好的寻优能力。SSAWLR对比其他算法来说，单峰值函数中除函数F5外的优化精度高出了大量数量级，说明其具有很好的寻优精度；多峰值函数中除函数F6外最优值最小，可见其具有良好的跳出局部极值的能力。固定维函数中除函数F11外，计算的方差最小，说明其具有良好的稳定性。综上分析，SSAWLR算法具有良好的性能及可行性且它的改进策略是有效的。

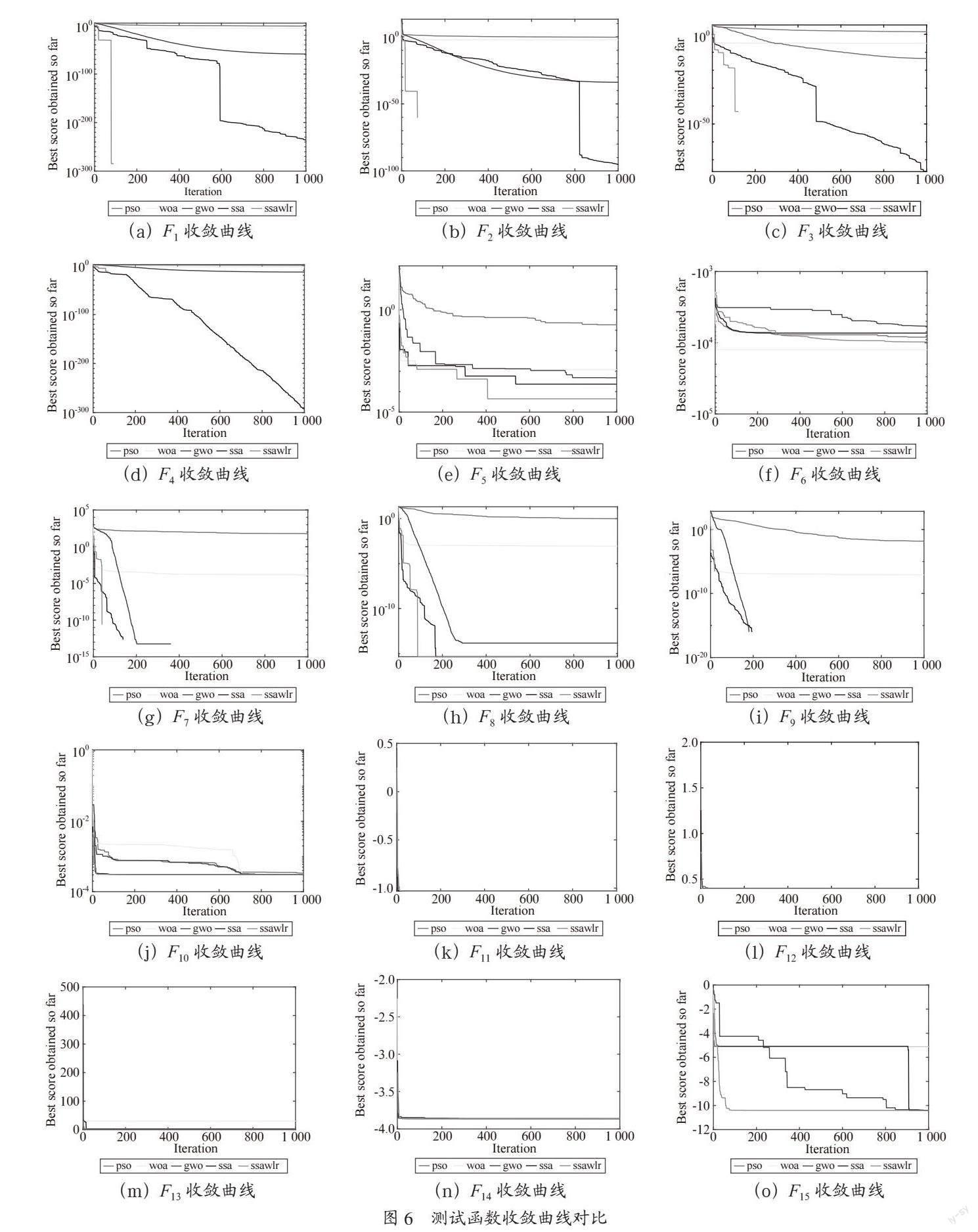
3.3  算法收敛曲线分析

收敛曲线能够更加直观地展示算法收敛的速度以及精度。由图6可知，SSAWLR算法在大多数测试函数中收敛的速度最快以及精度最高。从单峰值函数来看，SSAWLR均能快速迭代并获得最优值，可见其具有较快的收敛速度。除函数F6外的剩余测试函数来看，SSAWLR依然具有更好的寻优能力，并找到最好的适应度值。尤其在函数F7、F8中，SSAWLR均能在迭代50次之前到达理论最优值。综上，SSAWLR算法不仅具有快速的收敛速度还有更高的收敛精度。

4  基于SSAWLR和Taylor算法的协同定位方法

基于到达时间差（Time Difference of Arrival， TDOA）的迭代定位算法中以Taylor算法最为经典。该算法思想是通过不断迭代来修正待定目标位置的估计值，直到估计值逼近目标的真实位置坐标，所以它的精度极易受估计值的影响。本文采用SSAWLR进行估计值的预估，然后将结果带入Taylor中进行定位计算。本文适应度函数设计如式（12），评价函数则以均方根误差式（13）作为定位优劣的测度：

其中f1=p2-p1-r2，1，f2=p3-p1-r3，1，f3=p4-p1-r4，1，f4=p5-p1-r5，1。pi（i=1，2，3，4，5）是目标估计值到基站的距离，ri，1是目标到基站i与基站1距离差的测量值。（xkr，ykr）是第k个目标真实坐标，（xk，yk）是计算出的第k个估计位置，n是目标的个数。

为了验证本文所提SSAWLR-Taylor算法的性能，因此，与Chan[17]、Taylor、SSA_Taylor进行仿真对比。仿真实验基站坐标为（0，0）、、、、，并假设满足均值为0，且标准差分别为0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.10的具有理想高斯分布特性的测量误差。基站（0，0）作为中心基站，并以它为圆心，在其半径为7内随机生成100个目标坐标，同时把目标的横坐标与纵坐标分别加上[-1，1]区间上的随机数作为Yaylor定位算法的初值。SSA和SSAWLR麻雀种群规模为Num=100，最大迭代次数Max=50次，目标函数维度Dim=2，边界的上界和下界分别为Ub=7，Lb=-7，上述物理量的量纲单位均是千米。图6是不同测量误差（SD）下100个目标的均方根误差（RMSE）对比。

从图7可知，在不同测量误差下，即使目标的初次估计值距离目标坐标1 km内变化，Taylor算法的均方根误差依然高于Chan算法，更何况初次估计值离目标较远时，Taylor就更难完成目标坐标定位。而SSA_Taylor和SSAWLR_Taylor的定位效果优于Taylor算法，它们的均方根误差和闭式解的Chan算法接近，说明它们都提供了高质量的初代估计值，进而很大程度上增加了Taylor算法的定位精度。由此可见，SSAWLR和SSA分别与Taylor算法的融合是有效可行的，并且使得Taylor在有限次迭代内具有闭式解的精度。

5  结  论

本文提出了一种融合逻辑回归的麻雀算法，该算法引入了四种策略：SSM映射、逻辑回归函数、步长因子、改进的边界控制。该算法克服了初代种群多样性欠缺、发现者和跟随者数量利用率低及收敛速度缓慢的缺陷。测试函数结果反应了该算法有良好的性能和普适性。Taylor初值估计的结果表明了该算法具有好的实用性。

SSAWLR_Taylor有很好的优化性能，但仍有不足之处。比如算法跳出极值点的能力较弱及某些性能指标较差且不稳定。针对不足之处，今后还需要做一些工作：一是，如何增强算法的全局开发能力。二是，如何提高算法的稳定性。三是，如何有效利用越界個体携带的信息。

参考文献：

[1] CHEN J F，WANG L，PENG P. A collaborative optimization algorithm for energy-efficient multi-objective distributed no-idle flow-shop scheduling [J/OL].Swarm and Evolutionary Computation，2019，50（C）：100557[2022-08-09].https：//doi.org/10.1016/j.swevo.2019.100557.

[2] LIU W，GONG Y，CHEN W，et al. Coordinated Charging Scheduling of Electric Vehicles：A Mixed-Variable Differential Evolution Approach [J].IEEE Transactions on Intelligent Transportation Systems，2020，21（12）：5094-5109.

[3] ZHOU S，XING L，ZHENG X，et al. A Self-Adaptive Differential Evolution Algorithm for Scheduling a Single Batch-Processing Machine With Arbitrary Job Sizes and Release Times [J].IEEE Transactions on Cybernetics，2021，51（3）：1430-1442.

[4] XUE Y，ZHANG Q，ZHAO Y. An improved brain storm optimization algorithm with new solution generation strategies for classification [J/OL].Engineering Applications of Artificial Intelligence，2022，110：104677[2022-08-09].https：//doi.org/10.1016/j.engappai.2022.104677.

[5] ARORA S，SINGH S. Butterfly optimization algorithm：a novel approach for global optimization [J].Soft Computing，2019，23（3）：715-734.

[6] ARORA S，ANAND S. Chaotic grasshopper optimization algorithm for global optimization [J].Neural Computing and Applications，2019，31（8）：4385-4405.

[7] XUE J，SHEN B. A novel swarm intelligence optimization approach：sparrow search algorithm [J].Systems Science & Control Engineering，2020，8（1）：22-34.

[8] 張九龙，王晓峰，芦磊，等.若干新型智能优化算法对比分析研究 [J].计算机科学与探索，2022，16（1）：88-105.

[9] 吕鑫，慕晓冬，张钧，等.混沌麻雀搜索优化算法 [J].北京航空航天大学学报，2021，47（8）：1712-1720.

[10] 欧阳城添，朱东林，王丰奇，等.基于折射麻雀搜索算法的无人机路径规划 [J].电光与控制，2022，29（6）：25-31.

[11] YAN S，YANG P，ZHU D，et al. Improved Sparrow Search Algorithm Based on Iterative Local Search [J].Computational Intelligence and Neuroscience，2021，2021：1-31.

[12] 朱明豪.基于1D离散混沌映射的组合系统研究 [D].长沙：湖南大学，2020.

[13] KENNEDY J，EBERHART R C. A discrete binary version of the particle swarm algorithm [C]//1997 IEEE International conference on systems，man，and cybernetics. Computational cybernetics and simulation. IEEE，1997：4104-4108.

[14] MIRJALILI S，LEWIS A. The whale optimization algorithm [J].Advances in Engineering Software，2016，95：51-67.

[15] MIRJALILI S，MIRJALILI S M，Lewis A. Grey Wolf Optimizer [J].Advances in Engineering Software，2014，69：46-61.

[16] FOY W H. Position-Location Solutions by Taylor-Series Estimation [J].IEEE Transactions on Aerospace and Electronic Systems，1976，AES-12（2）：187-194.

[17] CHAN Y T，HO K C. A simple and efficient estimator for hyperbolic location [J].IEEE Transactions on Signal Processing，1994，42（8）：1905-1915.

作者简介：彭一凯（1990—），男，苗族，湖南怀化人，硕士研究生在读，主要研究方向：目标识别与跟踪、多点定位；蒲红平（1975—），男，汉族，四川广安人，副教授，博士，主要研究方向：大数据分析、智能控制、智能信号分析与处理、工业自动化研究与工程应用。