基于人工神经网络算法的自拟清瘟方制备工艺优化探索*

马诗瑜，何敬成，詹陆川，林伟杰，林思濠，5，胡小刚，卞晓岚△

（1. 上海交通大学医学院附属瑞金医院，上海 200023； 2. 南方医科大学顺德医院，广东佛山 528000；3. 广东省人民医院，广东广州 510000； 4. 广东省珠海市人民医院·暨南大学附属珠海医院，广东珠海519099； 5. 上海健康医学院药学院，上海 201318； 6. 重庆大学附属肿瘤医院，重庆 400030）

人工神经网络算法的主要特点是模仿人脑处理信息，具有自学习、自组织、自适应能力［1-2］，很强的容错能力，分布储存与并行处理信息的功能及高度非线性表达能力［3-4］。与正交试验法相比，神经网络具有学习规则、自我训练的能力，在给定区域内或预测网络下均可进行优化［5］，使试验结果更可靠、稳定，且无须目标函数具备明确的数学表达式，就可快速得到最优解［6］。本研究中以自拟清瘟方为例，通过多种神经网络算法对其水提工艺正交试验结果进行进一步预测，并对提取条件参数进行优化，旨在完善和弥补正交试验中的不足，如解答正交试验中无法处理缺失值、存在局部最优解等困惑，以期最终降低中药制剂尤其是医疗机构制剂的开发成本、节省工艺验证成本等。

1 水提工艺正交试验

本方临床以水煎剂应用，故以水为溶剂，以传统煎煮方法制备样品。按处方量称取全方药材（金银花9 g，鱼腥草、板蓝根、大青叶、贯众各15 g），分别取9 份。参照2020 年版《中国药典（一部）》，以料液比（因素A）、提取时间（因素B）、提取次数（因素C）为考察因素，以绿原酸、木犀草苷、靛蓝、靛玉红含量，干膏得率及综合评分（采用加权评分法计算得到）为考察指标进行L9（34）正交试验，确定最佳提取工艺。设定干膏得率及靛蓝、靛玉红、绿原酸、木犀草苷含量的加权系数分别为0.2，0.1，0.3，0.1，0.3，综合评分=（干膏得率/干膏得率最大值× 0.2 + 靛蓝含量/靛蓝含量最大值× 0.1 +绿原酸含量/ 绿原酸含量最大值× 0.1 + 木犀草苷含量/木犀草苷含量最大值×0.3+靛玉红含量/靛玉红含量最大值×0.3）×100。因素与水平见表1，正交试验设计与结果见表2，极差分析结果见表3，方差分析结果见表4至表6。

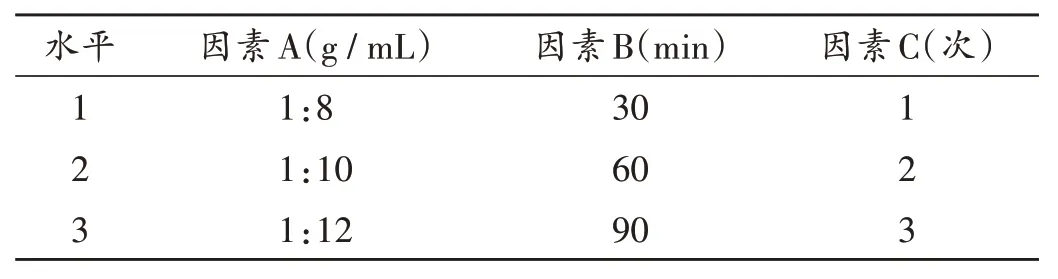
表1 因素与水平Tab.1 Factors and their levels

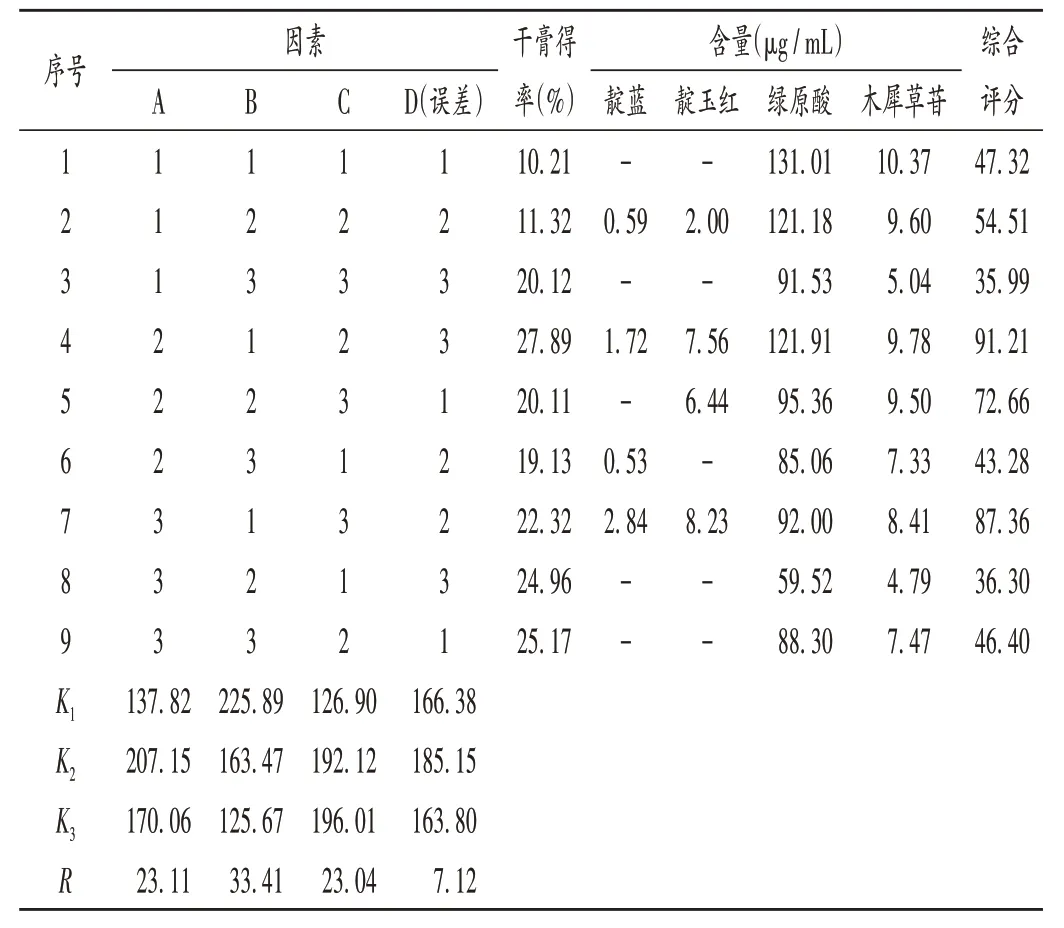
表2 L9（34）正交试验设计与结果Tab.2 Design and results of the L9（34）orthogonal test

表3 极差分析结果Tab.3 Results of the range analysis

表4 综合评分值的方差分析结果Tab.4 Results of the ANOVA of comprehensive score

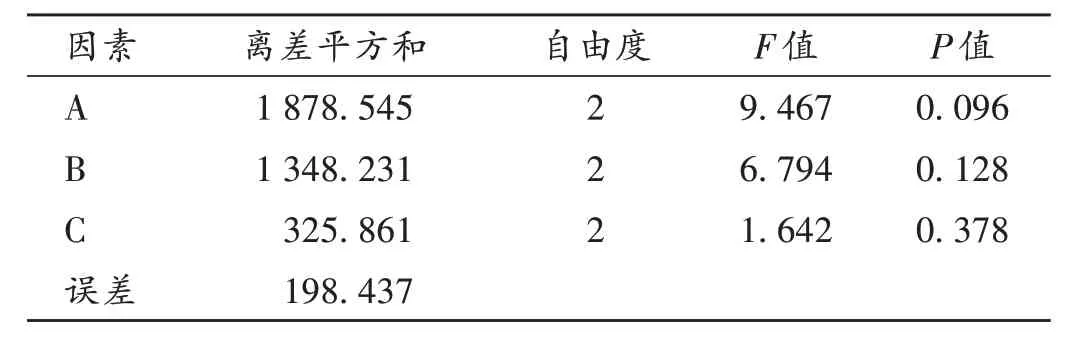
表5 绿原酸含量的方差分析结果Tab.5 Results of the ANOVA of chlorogenic acid content

表6 木犀草苷含量的方差分析结果Tab.6 Results of the ANOVA of luteoloside content

可见，以不同指标分析可能得到不同的制剂参数，且发现影响提取条件的权重也不完全相同。对于不同的指标（综合评分值、绿原酸含量、木犀草苷含量），不同的处理影响因素对结果均无显著影响。且存在未测出的值时（靛蓝和靛玉红含量），无法准确进行相应的方差分析和极差分析。以综合评分值为例，最优方案为A2B1C3及A2B1C2。而以绿原酸、木犀草苷含量为评价指标时，最优方案分别为A1B1C2和A2B1C2，暂定为A2B1C2，即料液比1∶10（g/mL），提取2 次，每次30 min。此外，设计综合评分时，对所有有效成分的权重权衡后设定了不同的加权系数，也会在一定程度上影响综合评分结果。

可见，对正交试验的结果使用极差分析和方差分析时，会因选择不同的指标而出现结果不一致的情况，造成无法选取最优提取参数的情况。故有必要引入神经网络算法筛选提取参数。

2 神经网络训练

2.1 样本选择

本研究中采用前期正交试验得到的9组样本数据，但为获得更可信的神经网络预测结果，因此增加了虚拟样本量进行训练，在实际生产中，由于原料产地、批次差异、操作条件不同，检测仪器本身的原因等，输入变量和实际值会存在微小但不可避免的误差，在此误差范围内的输入值与输出值应对应。虚拟样本的生成方法是在每个实际样本的数据上增加一个±Δi值，本研究中Δi取±0.1%，使每个实际样本产生9 个虚拟样本，由此参加神经网络训练的样本共90 个，增加了训练空间内的样本密度。

2.2 测试方法

采用多层感知器?（MLP）神经网络算法、反向传播（BP）和径向基（RBF）神经网络算法、遗传算法（GA）-BP神经网络算法以正交试验中3种因素水平为输入，6种指标（Gel、L、M、Q、H、综合评分值S）为输出，随机抽取70%样本进行训练，剩余样本进行测试。BP及RBF神经网络设定最大训练次数为1 000 次，隐藏层神经元设定为9，GA-BP网络设定最大训练次数为5 000次，设定2个隐藏层，隐藏层神经元设定为5和6，通过误差平方和决定遗传迭代次数。通过决定系数R2可评价模型拟合的优与劣。

2.3 训练结果

MLP 神经网络算法：共训练了66 个样本（73.33%），测试了24 个样本（26.67%）。建立的神经网络为2个隐藏层，隐藏层1，2中的节点数分别为5个和4个，训练集中的平方和误差为5.803，标度因变量的相对误差分别为0.12（L）、0.032（S）、0.062（Gel）、0.096（Q）、0.005（H）、0.126（M）。测试集中的平方和误差为2.561，标度因变量的相对误差分别为0.108（L）、0.021（S）、0.288（Gel）、0.027（Q）、0.004（H）、0.091（M）。该神经网络中认为影响因素的权重大小为B>A>C（图1）。对该神经网络的预测值与原始实际值进行比较，得出残差图，图中越接近0，表示预测结果越准确（见图2）。MLP 预测中样本的平均误差率较大，分别为8.07%（Gel），9.41%（Q），4.37（L），20.75%（H），6.77%（M）和9.19%（S）。因此，应考虑进一步选择其他的神经网络进行预测和优化。

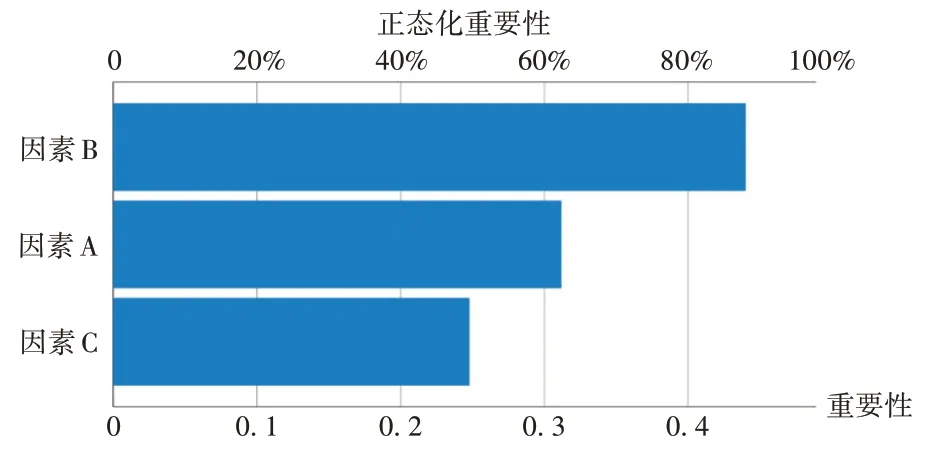
图1 MLP神经网络分析的因素重要性Fig.1 Importance of factors by the MLP neural network

BP神经网络和RBF神经网络算法：输入参数见图3。干膏得率、绿原酸含量、木犀草苷含量、综合评分值的预测中，BP 神经网络算法的R2值均明显优于RBF 神经网络，而靛蓝和靛玉红含量中RBF 神经网络算法的R2以微弱优势优于BP 神经网络算法。相对误差率，BP 神经网络和RBF 神经网络算法的平均相对误差率对于每个指标分别为0.12%/ 0.2%（Gel）、1.15%/ 0.10%（Q）、0.18%/ 0.26%（H）、0.05%/ 4.57%（L）、0.13%/1.75%（M）、0.072%/ 0.46%（S），详见图4。可见，使用BP 神经网络进行预测，将获得更小的误差和更优的决定系数。但BP 神经网络算法的预测中发现存在局部最优解问题，即不同的指标得到不同的最好优化参数，但无法通过6个指标给出统一的优化参数，故使用遗传算法进一步解决该问题。

图3 不同指标的BP和RBF神经网络算法的输入参数A.Gel B.Q C.H D.L E.M F.SFig.3 Input parameters of different indicators by the BP and RBF neural networks

图4 BP神经网络和RBF神经网络预测值及决定系数的比较A.Gel B.Q C.H D.L E.M F.SFig.4 Comparison of predicted value and R2 between the BP and RBF neural networks

GA-BP 神经网络算法：输入参数见图5。遗传迭代到60 次后，误差平方和最小（图6），不同指标中预测值与实际值（图7、图8）的均方误差分别为0.28（Gel）、0.000 021（Q）、0.000 088（H）、0.022（L）、0.000 83（M）和0.23（S）。最优参数及最优预测值分别为：料液比0.099（g/ mL），提取时间29.97 min，提取次数2 次，Gel：27.81，Q：1.72，H：7.56，L：121.84，M：9.79，S：91.07。GA - BP 神经网络预测出的最优参数与正交试验方案一致。

图5 GA-BP神经网络输入参数Fig.5 Input parameters by the GA - BP neural network

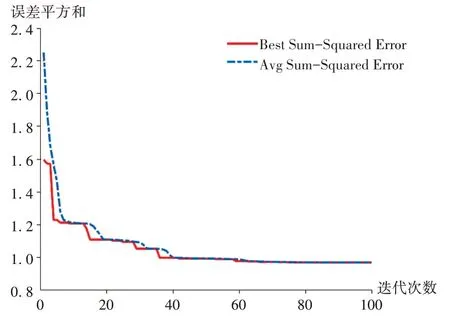
图6 遗传迭代次数Fig.6 Genetic iteration times

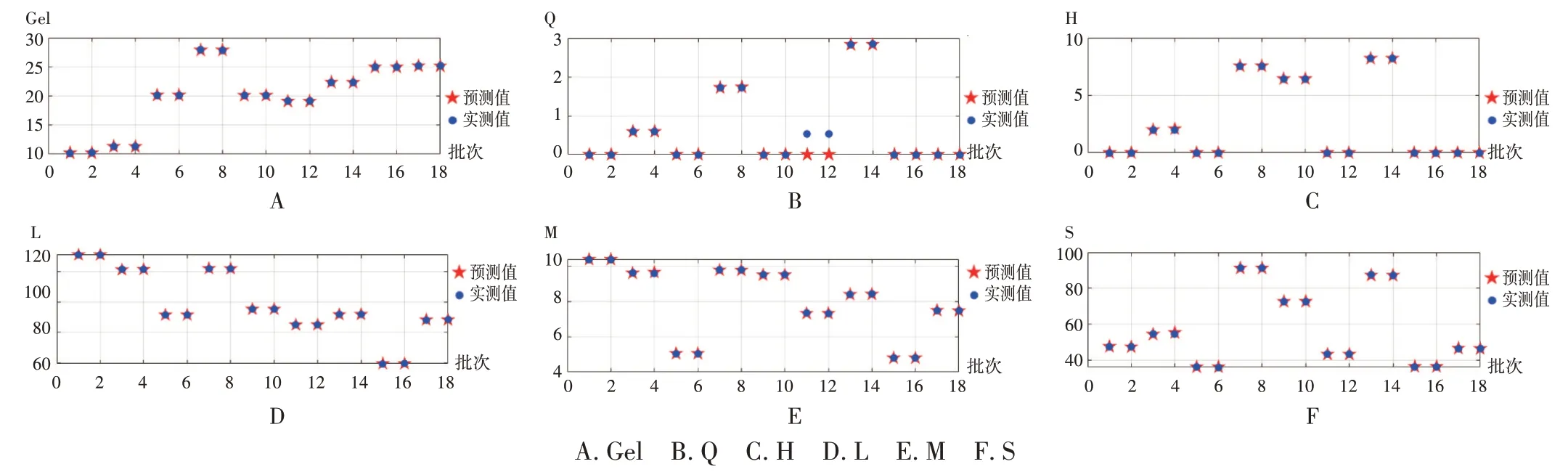
图7 GA-BP神经网络算法预测结果A.Gel B.Q C.H D.L E.M F.SFig.7 Results of prediction by the GA - BP neural network

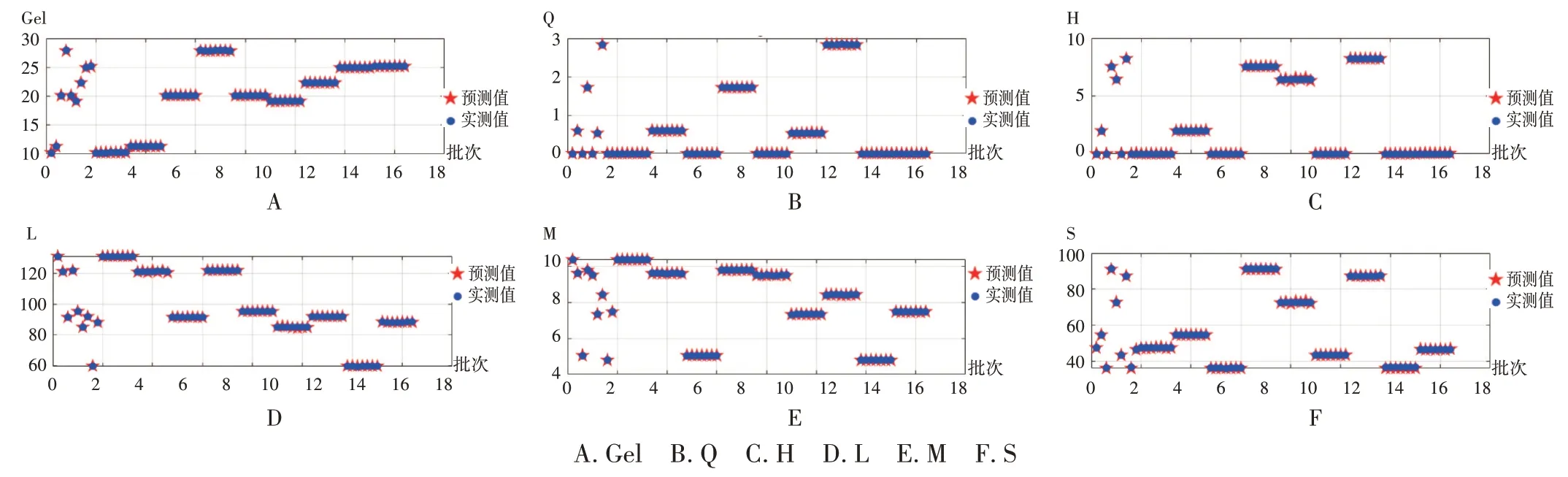
图8 GA-BP神经网络算法训练结果A.Gel B.Q C.H D.L E.M F.SFig.8 Results of training by the GA - BP neural network

3 验证试验

通过正交试验和GA - BP 神经网络的预测，暂定2种最优工艺，分别为A2B1C2和A1B1C2，现同时对2种工艺进行验证试验，结果见表7。可见，前法各方面结果均高于预测值，因此确定为最终工艺。

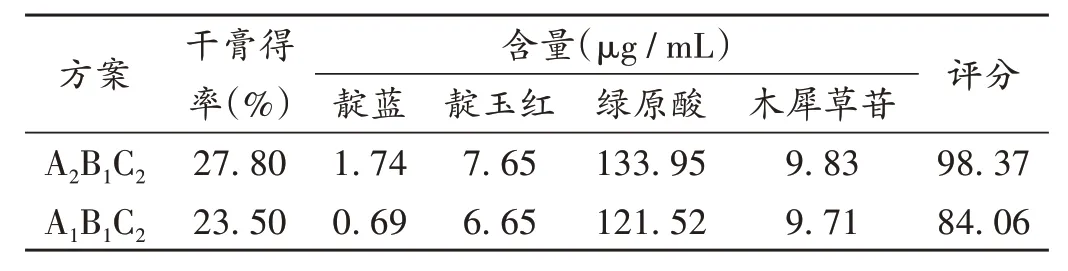
表7 验证试验结果（n=3）Tab.7 Results of the verification test（n=3）

4 讨论

本研究中主要基于前期正交试验中发现的不足之处而进一步设计人工神经网络进行提取参数的筛选。正交试验中，影响不同输出指标的输入指标权重各不相同，且统计过程中不同的统计方法得出不同的结果。综合评分值极差分析中发现，影响的权重为B>A>C。但方差分析中发现，影响的权重为B>C>A，由于综合评分值中，提取时间和提取次数的R值较接近，又均无显著差异，也可认为两者均对综合评分值有次要影响作用。木犀草苷的分析中，极差分析（图1）中发现，影响的权重为B > A = C，可能是后两者得到的提取结果中差值一致的结果所致。而方差分析影响权重为B>A>C，两者最优方案一致为A2B1C2。另外，由于本试验中靛蓝和靛玉红的含量较低，有未测出的情况，因此在综合评分值的考虑时，对所有有效成分的权重进行了权衡，但发现不同指标的最重要影响因素也不同，综合评分值和木犀草苷是提取时间，绿原酸是料液比。为克服上述不足，本研究中采用了不同神经网络（MLP，BP，RBF，GA-BP）算法对正交试验结果进行优化。

MLP 神经网络作为一种接近深度学习的网络模型（复杂、多层的神经网络），其具有出色的非线性匹配能力和泛化能力、较高的并行性，以及能全局优化［7］。缺点是在高维空间效率低，易出现过拟合现象，收敛缓慢且计算量高［8］。本研究中，初始考虑该神经网络具有全局优化的优点而使其进行参数优化，设定隐层数为2 个，MLP 网络的隐层能实现非线性样本的线性转化，从而实现样本的分类预测，且有研究证实，多层网络能获得更精准的分析结果，但使用2 个以上的多个隐层网络时，可能使模型不易得到最优解。一般深度学习模型需较大的数据量，虽然本研究的隐层设定理论上能达到较准确的预测，但考虑到可能因样本量较小而导致拟合结果不佳，因此考虑使用其他神经网络进行优化。

BP 神经网络作为最经典的神经网络算法，使用梯度下降的局部优化技术，具有多层网络体系，使输出更准确；梯度下降局部优化技术，与网络权重的向后误差校正相关［9-10］。标准BP 算法常有两点局限性：在误差曲面上有些区域平坦，此时误差对权值的变化不敏感，误差下降缓慢，调整时间长，影响收敛速度；存在多个极小点，多维权值空间的误差曲面存在多个局部极小点，它们均有误差梯度为0 的特点。RBF 神经网络被认为是BP神经网络的进一步优化，主要体现在逼近能力、分类能力和学习速度更优。

RBF 神经网络主要用隐层节点通过基函数执行一种非线性变化，将输入空间映射到一个新的空间，输出层节点则在该新空间实现线性加权组合［11］。该网络具有独特的分类预测原理，对非线性连续函数具有一致逼近性，易于大范围的数据融合和并行高效处理。本研究中进一步使用RBF 神经网络，正是基于其对数据融合和预测的能力。该神经网络学习收敛速度快，计算量小；操作简单，结果直观。然而该函数需恰当的数据中心与合适的RBF 函数，往往不易获得更合适的函数［12-13］。在本研究中，其预测结果不如BP 神经网络理想，可能是未获得合适的径向基函数，且RBF 网络具有“局部映射”的特性，其网络输出与数据中心离输入模式较近的“局部”隐节点关系较大。

本研究在BP 神经网络的预测中，已使每个预测指标获得了更小的误差和更优的决定系数。但无法通过6 个指标给出统一的优化参数，因此在此基础上结合了GA。GA 是一种基于人工智能的随机非线性优化形式，可无须知道目标的具体数学模型而模拟出最优解，遗传算法结合神经网络的设计方法能避免正交试验易产生局部最优解的问题，更适合于达到全局最优组合设计的目标，是一种比正交试验更广泛和准确的模型。采用2 种方法结合的方式对提取参数进行优化［14-15］，可以其独特的模式识别、预测与模拟等能力为基础，在处理这类复杂问题时展现出强大的适应性。

本研究中采用了多种神经网络进一步对正交试验所得最优提取参数进行优化，并最后选择GA-BP神经网络对制剂中的提取参数进行优化和设计，通过模仿大脑的神经网络行为特点对数据进行处理，其利用实测数据对试验过程进行模拟，减少人为因素造成的分析偏差，可弥补正交试验的一些缺陷。通过该方法的预测和验证，可减少制剂的开发成本，尤其是节省工艺验证成本。但神经网络算法的应用与选择有待进一步研究。