基于GAN的多变量时间序列异常检测方法

姚 珺

（铜陵学院 数学与计算机学院，安徽 铜陵 244061）

多变量时间序列异常检测[1]在工业控制、医疗诊断、网络安全等应用领域中被广泛研究和关注，旨在通过构建以往时间序列变化的正常模式，以检测数据中不符合预期模式的时序片段[2]。例如，在网络安全领域，通过监测网络流量可有效地检测出用户的异常行为，从而保护系统免受网络攻击。时间序列异常检测通常会面临两大难题：一是在采集的样本中，异常数据远比正常数据少；二是样本标签通常需要由相应领域的专家进行人工标注，但给所有样本都打上标签很难实现。因此，仅用正常数据即可训练模型的无监督方法更适合时间序列的异常检测。

近年来，生成对抗网络（Generative Adversarial Networks,GAN）[3]备受关注。作为一种无监督的深度学习模型，GAN在高维数据建模方面具有优势，因而被广泛应用于时序数据的异常检测。基于GAN的异常检测方法通常分为两个阶段：模型训练阶段和异常检测阶段。在训练阶段，只使用正常数据来训练模型，逐步学习正常时序数据的分布特性，使得训练后的模型能理想地重构正常数据；在测试阶段，以样本重构误差作为判别依据，重构误差偏大的数据被将判定为异常。具体来说，根据模型输出的异常分数来判断样本是否为异常，且异常分数越高则样本是异常的可能性就越高。

从重构角度出发，按隐空间变量的生成方式，基于GAN的异常检测模型大致分为三种：第一种是不使用编码器（Encoder）生成隐空间变量的方法。与标准GAN一样，仅通过生成器和判别器来构造GAN，并对随机生成的隐变量进行优化，以生成与异常检测对象测试数据最相似的数据。代表模型有MADGAN[4]，该方法以LSTM-RNN网络作为GAN的基本模型来捕捉多变量时间序列分布，并设计同时考虑判别损失和重构损失的异常分数检测。第二种是使用双向GAN[5]（Bidirectional GAN,BiGAN）的方法。BiGAN是在标准GAN中添加编码器，从而使模型具备学习真实数据到隐空间逆映射功能，因此在训练时可以实现数据空间和隐空间的双向映射，从而生成用于重建测试数据的隐变量。代表模型有ALAD[6]，该方法在特征维度较高的大数据集上表现优异。第三种是使用自编码器（Auto-encoder）的方法。该方法通过自编码器来构造生成器，与BiGAN一样，在训练时可以实现学习数据空间与隐空间的双向映射。代表模型有BeatGAN[7]，该方法通过使用一维CNN或全连接神经网络来构造自编码器，有效提高了对单变量和多变量时间序列异常检测的精度。

由于多变量时间序列固有的高维复杂特性，其异常检测仍然是一个很大的挑战。本文提出了一种基于GAN的多变量时间序列异常检测模型。该模型使用长短期记忆（Long Short-Term Memory,LSTM）网络作为基本模块，生成器采用编码-解码结构，在模型训练时可以学习数据空间和隐空间的双向映射。因此，在异常检测阶段无需对每个测试样本进行隐空间变量优化，从而缩短了模型检测异常的时间。此外，在编码器、解码器和判别器中均加入一个多通道注意力（Multi-Channel Attention）[8]层，以学习多变量时间序列时空上的复杂依赖关系，并通过捕捉时序数据在时间和空间维度的重要性，从而提升异常检测的准确性。该模型结合生成器的重构损失和判别器的判别损失共同定义的异常分数来检测异常，同时在公开数据集上进行实验并验证了本文模型的有效性。

1 问题定义

本节给出了本文所使用的符号和问题定义。X=(…,xt,xt+1,…)∈Rn×d,d>1被称为多变量时间序列数据，其中，n表示时序数据的长度，xt∈Rd表示t时刻的时序向量，d表示时序向量的维度。

定义1多变量时间序列片段是指作为待训练或待检测的时序数据集合。

本文通过滑动窗口机制[9]从原始的多变量时间序列中提取时间序列片段。滑动窗口包含两个属性：窗口大小w和滑动步长s。将滑动窗口与时序数据起始处对齐，并沿着时序方向滑动。在每次滑动后，滑窗选中的数据即为一个时序片段。Xi=(xt-w+1,…,xt-1,xt)∈Rw×d表示滑窗移动了i步后所提取的时序片段，其中，t表示提取时序片段中时序数据的结束时刻，w表示时序片段的长度。给定多变量时间序列数据X的一个时间序列片段Xi，则多变量时间序列异常检测的目标是得到t时刻的异常分数，该异常分数可反映t时刻时序点的异常程度。

2 异常检测模型设计

针对多变量时间序列数据的高维度和复杂性，本文基于GAN提出了一种无监督多变量时间序列异常检测模型。为更好地学习时间序列分布，本文使用LSTM网络来构造生成器和判别器以捕捉多变量时间序列的特征。生成器采用编码-解码结构，在模型训练时可以实现数据空间和隐空间的双向映射。此外，在各网络中引入多通道注意力机制，以捕捉多变量时序数据不同维度的重要性，且学习多变量时间序列在时间和特征维度上的复杂依赖关系。

2.1 模型介绍

多变量时间序列数据异常检测旨在识别待测样本是否符合一段时间内数据的正态分布，将不符合要求的观测结果视为异常[10]。相关研究已成功应用GAN框架且实现异常检测，并验证了利用隐空间来重建待测样本进行异常识别的有效性[4-7]。本文在已有工作基础上，提出了基于GAN的多变量时间序列数据异常检测模型，如图1所示，整个网络分为两部分：一个生成器G和一个判别器D。其中，生成器G由一个编码器GE和一个解码器GD组成。异常检测方法分为两个阶段：模型训练阶段和异常检测阶段。

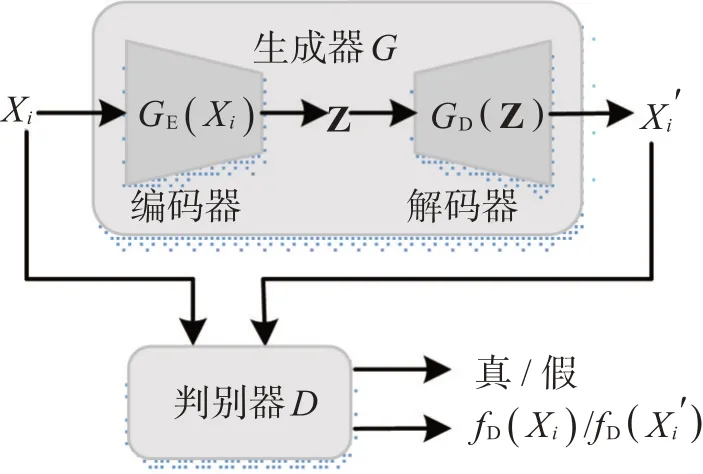
图1 模型结构

模型训练阶段只使用正常样本进行参数优化以学习正常数据的分布。首先，通过编码器GE将经过预处理的时序片段Xi映射到隐空间中，并输出其低维特征Ζ。然后，解码器GD将隐变量Ζ重构回原始数据空间，并输出重构样本最后，将重构样本和原始样本Xi输入判别器D来进行正则化处理，对原始特征和重构特征进行判别。生成器G和判别器D通过交替优化的方式来实现对抗博弈，最终生成可以近似表示真实数据分布的概率。异常检测阶段使用训练过的模型对测试样本进行异常检测。测试样本包含正常数据和异常数据，其预处理方法跟训练阶段相同。具体来说，首先将测试样本输入到模型中，然后使用模型输出的异常分数，并根据预先设定的阈值判断样本是否异常。本文采用生成器重构样本与原样本间的误差和判别损失来共同定义异常分数。由于模型只使用正常样本进行训练，故没有学习到异常样本的隐含特征和模式，因此在推理过程中，异常样本和其重构样本间的误差会非常大。当测试样本通过模型输出的异常分数超过阈值时，则可将其判断为异常样本，从而实现异常检测。

2.2 Attention层

多变量时间序列中不同时刻的数据之间具有时间相关性，而同一时刻的不同变量之间也具有空间相关性，充分利用数据间的时空相关性将更有利于提升异常检测的准确性，从而避免误判。本文采用文献[8]的多通道注意力机制，在编码器、解码器和判别器网络中均加入一个Attention层（图2），分别计算数据中时间和空间维度的重要性。

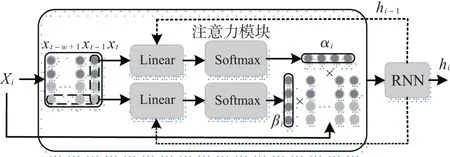
图2 Attention层结构

利用由RNN在过往时间序列中提取的特征，分别计算输入数据时间和空间维度的重要性。时间维度的重要性权重αi可由公式（1）和公式（2）计算，有

同样，空间维度的重要性权重βi可由公式（3）和公式（4），有

2.3 生成器模块

与文献[7]类似，本文通过自编码器来构造生成器，其目标是通过编码和解码的方式得到重构样本，即使用编码器将输入样本映射到一个隐空间中，然后使用解码器凭借隐空间以重建样本序列。编码器和解码器均使用相同结构，由3个子网络组成：Attention层、LSTM层和Linear层。LSTM通过一个特殊的存储单元来学习数据的远程依赖关系，已广泛应用于学习时间序列的时间相关性[4]。同时，Attention层计算输入时序片段的时间和空间维度的重要性权重，输出对输入进行加权后的数据；LSTM层捕捉由Attention层加权的数据特征之间的相关性和时间依赖性；Linear层对LSTM层输出各时刻的每个特征向量进行独立映射。具体来说，给定时序片段Xi，编码器GE输出将Xi映射到隐空间变量Z∈Rw×L。Ζ是Xi的低维特征表示，L是隐变量的维度。给定隐变量Z，解码器GD输出，将Z映射回原始数据空间，而是Xi的重构结果。

为了训练生成器，本文模型定义了3个损失函数：对抗损失、判别损失和重构损失。

生成器G需要捕捉输入样本的分布，生成尽可能服从真实数据分布的样本。因此，对其优化的目标是希望其能够生成尽量服从分布p(Xi)的真实样本，使得判别器D将不再能区分样本是来自于真实样本分布p(Xi)还是来自于生成器G生成的样本G(Xi)。对抗损失La的定义如

式中D(Xi)是判别器D输出的概率，其表示输入样本Xi是真实样本的概率。

在GAN中，生成器和判别器为使彼此的损失最小化而相互竞争，导致训练过程的稳定性降低。本文采用特征匹配（Feature Matching）[11]损失，通过直接优化训练数据与生成数据之间特征的平方差损失，使得GAN能够学到更多的真实数据分布信息以实现模型训练稳定性。判别损失Lf的定义如

式中f(Xi)是判别器D的LSTM 层输出单元的值。

为使生成器G提供更好的序列重建能力，本文模型使用重构损失来表示X和G(Xi)数据间的差异，定义为输入Xi与生成器输出的重构样本G(Xi)之间的L1距离。重构损失Lr的定义如

在训练过程中，将以上3个损失函数加权求和，并利用加权求和后的联合损失函数来训练模型。联合损失函数LG定义如

式中α、β和γ是调节参数，用于确定不同损失函数的权重。

2.4 判别器模块

本文利用对抗性训练学习给定样本的数据分布，需要同时训练一个生成时间序列数据的生成器和一个学会区分生成的样本与真实样本的判别器。为了有效处理时间序列数据，判别器D使用与编码器类似的架构，其由4个子网络组成：1个Attention层、1个LSTM层和2个Linear层。网络的前三层起到与编码器相同的作用，不同之处在于第三个Linear层输出Rw×1向量，其特征方向被映射为1。最后的全连接层将输入的特征向量在时间方向上映射为1，且考虑整个时间序列输入的概率并输出到判别器。具体来说，给定Xi或判别器D识别输入是真实样本还是由生成器重构的样本，即最大化fD(Xi)和fD(G(Xi))之间的差异，从而有效区分输入是真实样本或生成样本，并给出输入是真实样本的概率。判别器损失函数LD定义如

2.5 异常检测

为了实现异常检测，本文采取文献[4]的异常检测策略，即使用生成器生成的样本与输入样本的重构损失，以及判别器的判别损失来共同判定待测样本的异常情况。在给定待测样本数据后，先将其输入到已训练的GAN模型中并计算异常分数，若异常分数超过指定阈值，则判定输入样本存在异常。对于测试样本Xi，其异常分数A(Xi)定义为

其中λ是权重调节参数。计算出所有测试样本的异常分数后，应用公式（11）对异常分数进行归一化，将异常分数线性化为0到1的范围。最终使用产生的异常分数对测试样本进行评估，将得分超过阈值η的样本判断为异常样本，未超过的判断为正常样本。

3 实验验证

3.1 实验数据与基线方法

实验选取两个公开数据集HAR[12]（Heterogeneity Activity Recognition）和SWaT[13]（Secure Water Treatment）进行验证算法的性能。两个数据集均为多维时间序列数据，其中，HAR采集自可穿戴设备，SWaT采集自安全水处理仿真平台。对两个数据集分别进行了归一化，使其符合均值为0、标准差为1的高斯分布。所有数据集均被划分成训练集和测试集，详细信息如表1所示。实验选择CNN-1D[14]、LSTM-VAE[15]、BeatGAN[9]和MAD-GAN[4]作为基线方法。

表1 异常检测数据集描述

3.2 评估指标

采用精确率[16]（Precision）、召回率[16]（Recall）和F1 分数[14]来评估所有模型的异常检测性能，具体计算公式如下：

式中TP表示本身是异常样本，且被模型正确检测为异常样本的数量；FP表示本身是正常样本，但被模型错误地检测为异常样本的数量；FN表示本身是异常样本，但被模型错误地检测为正常样本的数量。精确率、召回率和F1分数的值越高，则模型性能越好。

3.3 实验设置

为了捕获数据的相关性，本文采取文献[17]的策略，通过滑动窗口机制将训练集与测试集的时间序列分别划分为时序片段的集合，其中窗口长度为30，移动步长为10。将步长设为小于窗口长度是为了增加训练样本数。实验中基线模型和本文模型的超参数配置如：CNN-1D 模型的编码器包含3 个一维CNN 层，卷积核大小分别为k1=8，k2=6，k3=4，filter maps 分别为f1=64，f2=128，f3=256。在每个CNN层之后使用LReLU激活函数和批量归一化计算。解码器是编码器的镜像映射，是使用转置卷积层取代卷积层。LSTM-VAE模型的编码器和解码器都包含两个隐藏层单元个数为16的LSTM层，训练批处理（Batch Size）大小为32。BeatGAN模型的隐变量维度为10。编码器、解码器和判别器均由全连接层神经网络构成，其中，编码器的网络层参数为256-128-32-10，解码器为10-32-128-256-1530，判别器为256-128-32-1。使用Adam优化器对模型进行梯度更新，其学习率（Learning Rate）为0.000 1。训练批处理大小为64，总轮数（Epochs）为300。MAD-GAN 模型的隐变量维度为15。生成器为100 个单元。LSTM 的层数为3，单元数为5。判别器为100个单元和1层，且用LSTM构建，全连接层为1个单元。生成器使用梯度下降优化，学习率为0.1。判别器使用Adam优化器，学习率为0.001。训练批处理大小为500，总轮数为100。本文模型的隐变量维度为32。每个中间层的单元数为128，LSTM层数为3。使用Adam优化器，学习率为0.000 2。判别器使用Adam优化器，学习率为0.000 2。训练批处理大小为100，总轮数为500。生成器损失函数的调节参数设为：α=1、β=0.1和γ=10。实验环境基于Windows 10操作系统，并使用Pytorch框架来实现实验模型及算法。实验平台的硬件环境：GPU为GTX 760显存，CPU为Intel i7 4790，内存为16 GB，硬盘为1 TB。

3.4 实验结果

在本文模型中，阈值η设置将直接影响模型检测的准确率。针对SWaT数据集，将阈值η以步长0.1进行增量变化，通过实验观察阈值选择对所有评估指标的影响，实验结果如图3 所示。可以看出，在SWaT 数据集中，精确率随着阈值η的增加不断上升，但F1分数在η大于0.6之后开始呈下降趋势，且召回率也明显下降。

图3 阈值η对模型性能的影响

使用四种异常检测模型与本文模型进行对比实验，对所有方法都使用相同的窗口长度和移动步长选择策略。为让精确率和F1值都尽可能大，在每一个数据集上找到最优F1分数下的检测阈值，使得其检测结果在各评价指标上均表现优异，并报告对应的精确率和召回率。表2对比了本文模型与各基线模型在两个实验数据集上异常检测的实验结果，可以看出，在实验条件相同的情况下，比较使用全连接层的CNN-1D和BeatGAN，以及使用LSTM层的LSTM-VAE和MAD-GAN，可以看出以对抗学习方式同时训练生成器和判别器的异常检测模型明显优于非对抗训练的异常检测模型，表明GAN在从数据集中捕获更复杂的结构和构建更精细的多变量时间和空间相关性方面具有优势，同时也验证了LSTM层对时间序列数据具有更高的表示能力。与基线模型相比，本文提出的异常检测模型在两种数据集上的异常检测性能均优于其它基线模型。相较于MAD-GAN，对于HAR数据集而言，在精确率、召回率和F1分数上分别提高了7.6%、11.8%和10.4%，对于SWaT 数据集而言，分别提高了0.8%、6.9%和5.2%。这是因为本文模型不仅可以让LSTM 层准确捕捉多维时间序列的特征，还可以让Attention层捕捉时序数据时间和空间维度的重要性。

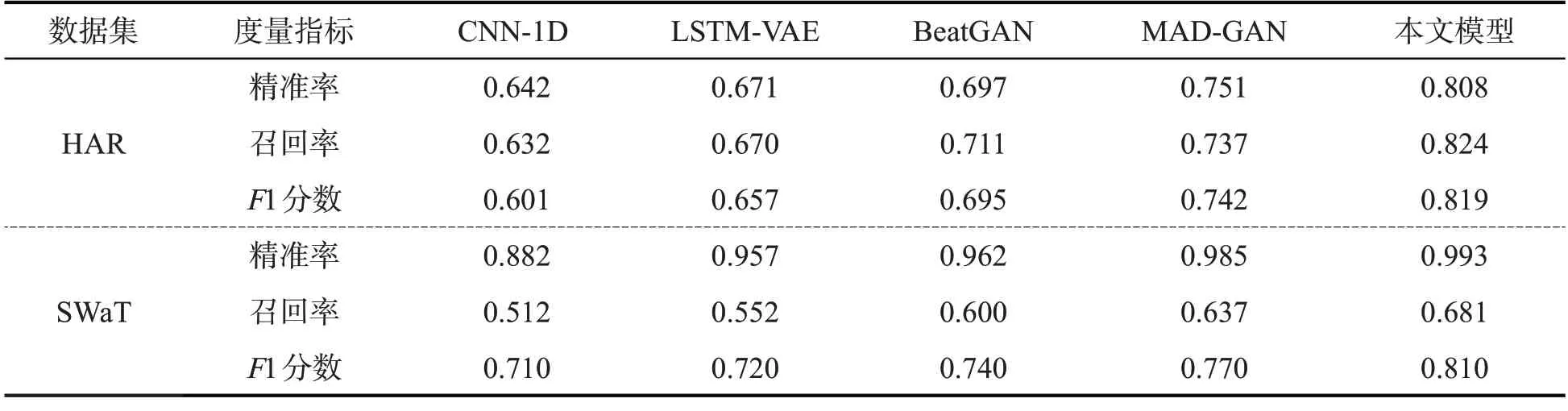
表2 异常检测的实验结果

4 结束语

本文提出了一种基于GAN的多变量时间序列无监督异常检测方法。该方法采用编码器和解码器来构造生成器，实现了时间序列数据空间和网络编码隐变量空间的双向映射，从而避免了异常检测阶段的优化过程。此外，网络所采用的注意力机制使模型能够专注于时序数据的重要特征。通过学习多变量时间序列的空间和时间关系并利用联合优化策略，有助于提升模型的异常检测能力。基于HAR和SWaT数据集实验验证了本文模型的有效性，与其他类似方法相比，本文模型展示了更好的异常诊断能力。