高考命题改革对优化数学教学的启示
2023-06-21陈中峰
陈中峰
一、高考改革的总体方向
2014年国务院发布的《关于深化考试招生制度改革的实施意见》吹响新一轮高考改革的号角,2016年教育部考试中心启动的“考试大纲修订”,提出了“一体四层四翼”的评价改革构想。经过几年高考命题改革的实践与探索,2019年12月教育部考试中心出台了《中国高考评价体系》,进一步将“一体四层四翼”重新表述为“一核四层四翼”,确立了“立德树人、服务选拔、导向教学”[1]这一高考的核心立场,回答了“为什么考”的问题,重申了“必备知识、关键能力、学科素养、核心价值”的四层考查目标以及“基础性、综合性、应用性、创新性”四个方面的考查要求,明确了高考“考什么”和“怎么考”的问题,提出了“价值引领、素养导向、能力为重、知识为基”的命题理念,形成了新时期“高考评价体系”。教育部考试中心明确指出“高考评价体系是高考命题、评价与改革的理论基础和实践指南,主要供高考命题人员、高考研究人员、教育考试管理人员以及广大师生学习参考使用”。2019年12月,教育部考试中心命题处各学科秘书分别在《中国考试》发表署名文章《基于高考评价体系的XX学科考试内容改革实施途径》,从“功能定位”“考查内容”“考查要求”“考查载体”等方面具体阐述了各学科高考命题改革的思路和内涵,强调问题情境是承载考查内容、实现考查要求的载体。2020年10月,中共中央、国务院正式印发的新中国第一个关于教育评价系统性改革的文件《深化新时代教育评价改革总体方案》进一步明确提出:深化考试招生制度改革,稳步推进中高考改革,构建引导学生德智体美劳全面发展的考试内容体系,改变相对固化的试题形式,增强试题开放性,减少死记硬背和“机械刷题”现象。至此,新一轮高考改革的方向清晰明朗。《中国高考评价体系》的出台标志着我国新一轮高考命题改革思路的成熟,引领着新一轮高考改革的总体方向。
二、新高考试题的突出特点
高考试卷最直接地反映了高考命题人员对《中国高考评价体系》的理解。那么,近年来高考试题有什么特点呢?
(一)立足基础,关注基础定义
根据“知识为基”的命题理念,新高考重视对“必备知识”等基础性问题的考查,特别是关注对核心概念、基础定义的考查。如,2021年全国新高考(I)卷第8题直接考查了事件相互独立的概念,第9题直接考查样本的平均数、中位数、标准差、极差等概念及其含义,第13题和第21题(1)分别考查偶函数和双曲线的定义等;2022年全国新高考(I)卷第6题考查正弦函数的周期、图象的对称中心的定义,第12题考查偶函数、导数的定义及导数的几何含义,第15题考查曲线的切线的定义等。
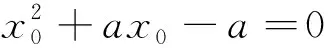
(二)聚焦能力,关注问题解决
聚焦关键能力,关注问题解决,是这两年高考试题的一个显著特点。试卷基本上杜绝有现成模式可以直接“套解”的问题,多数试题都必须经过考生自己的独立分析与思考,并综合应用识图作图、逻辑推理、数学运算等关键能力才能解决,关注对分析解决问题能力的考查,彰显“能力为重”的命题理念。就是基本题,也都需要考生在弄清问题本质的基础上,对问题进行合理的转化,

(三)强调应用,关注学以致用
能用数学的眼光看待生活、认识世界,从数学的角度提出问题、理解问题并综合运用数学知识和思想方法解决和处理身边的问题,既是每个公民应具备的基本素养之一,又是进入高校继续学习的基本能力要求之一。[2]新高考在关注基础性的前提下,注重体现数学的应用价值,强调基于真实背景创设问题情境,合理地设置一些具有较好现实意义的试题测量考生将知识迁移到现实情景的能力,检测考生运用知识分析问题和解决问题的能力。应该注意的是,目前应用问题的设置更加理性,不盲目追求实际情境试题的数量,且基本摆脱了那种“穿鞋戴帽”的假应用题,更加关注数学的本质,关注数学应用的实质,关注考查学生数学建模能力、应用数学模型解决问题的决策能力等。
例3.一种微生物群体可以经过自身繁殖不断生存下来,设一个这种微生物为第0代,经过一次繁殖后为第1代,再经过一次繁殖后为第2代……该微生物每代繁殖的个数是相互独立的且有相同的分布列,设X表示1个微生物个体繁殖下一代的个数,P(X=i)=pi(i=0,1,2,3).(1)已知p0=0.4,p1=0.3,p2=0.2,p3=0.1,求E(X);(2)设p表示该种微生物经过多代繁殖后临近灭绝的概率,p是关于x的方程:p0+p1x+p2x2+p3x3=x的一个最小正实根,求证:当E(X)≤1时,p=1,当E(X)>1时,p<1;(3)根据你的理解说明(2)问结论的实际含义.
评析:本题以现实问题为背景,考查学生将所学的统计概率、函数零点、导数等知识迁移到现实情境分析解决问题的能力。特别是第(3)问深入考查了学生对期望、概率等概念的理解程度,很好地检测“学以致用”的水平。
(四)突出情境,关注真才实学
关注问题情境的创设,坚持“无应用情境就无知识测试”的原则,坚持“以课程学习情境为检验基础的量尺,以探索创新情境为区分甄选的手段,以生活实践情境为拓展应用的渠道”,基本上杜绝了“裸考知识”的现象,让“测评”发生在知识处于生成状态或应用状态的情境中,着力检测学生的学科核心素养,关注学生的真才实学。

C.f(-1)=f(4)D.g(-1)=g(2)


同理,根据“g(2+x)为偶函数”也作出函数f(x)与g(x)图象的一种示意图:

由此得到2既是函数f(x)的一个周期,也是函数g(x)的一个周期,问题迎刃而解。
(五)科学布局,关注服务选才
新高考数学试卷为了实现为国选材的责任担当,立足“立德树人、服务选才、引导教学”的核心功能,坚守“素养导向,能力为重”的原则,不但通过合理设计问题情境、试题呈现方式等手段实现了强化对理性思维和关键能力的考查,使试卷呈现出“逻辑思维要求高”“运算能力要求高”“化归转化要求高”等特点,而且启用了“多选题”“多空题”“结构不良试题”等新题型,关注发挥开放性、创新性问题的选拔功能,进一步将哪些通过大量机械刷题的伪学霸甄别出来,使得真正“理解数学本质”的优秀学生得以脱颖而出。
三、优化数学教学的思考
新高考的数学试题更加关注发挥“立德树人、服务选才、引导教学”这一核心功能,关注人才选拔的科学性与有效性,关注发挥试卷的选拔功能。在对知识的考查上,基本上杜绝了停留在表面的“纯知识”考查,而是表现为深化对概念、定义的发掘,关注对知识内涵的考查,关注对隐含在教材练习题内部的解决问题的通性通法的考查,关注在真实情境中灵活应用知识分析解决问题的考查。这些改革必将对我们的日常教学提出新的要求,意义深远。
(一)关注知识内涵的挖掘与揭示
切实回归课标与教材,充分重视基础知识的教学,是新高考改革给予我们的重要启示之一。[3]它要求在基础知识的教学中,不盲目追求教学进度,不能认为基本概念、定义、法则、性质等相对简单就忽视对它们的讲解,而应引导学生经历对基本概念、原理、法则等的提炼过程,让学生在充分经历观察、思考、探究、总结等思维过程中领会知识的内涵,实现对基础知识的深度理解;在练习题的教学中,不能只展示例习题的解题过程,就题论题,缺乏必要的内涵发掘和合理的拓广延伸。
1.挖掘定义内在的深层涵义



2.揭示例题内隐的思维方法
由于新高考立足国家人才选拔的战略需要,关注高校的人才选拔要求,突出了对创新型人才的甄选。因此,新高考的命题关注创新试题形式,优化试题设计,设计了一系列没有现成模式可以直接套用的问题,减少学生反复刷题、机械训练的收益,着力检测学生的核心素养和真实的学力水平,鼓励学生运用创造性、发散性思维分析问题和解决问题。[4]因此,例题教学绝不能停留在就题论题上,仅仅让学生明白解法,而要以“例题”为“例”,通过对例题的剖析,让学生不但明白该题的解法,而且弄清该题为什么这么解、其思路是怎么产生的,使学生通过例题的学习,不但巩固了基础知识、深化对基本概念、原理等的理解,而且从中学会分析解决问题的普适性方法,并能应用这些方法分析解决其他问题。[5]

评析:这是人教A版教材183页的例题7.如何用好这个例题呢?好多教师认为本题很简单,直接按照教材的顺序给出如下解法.
证法1:由cosx≠0,知sinx≠-1,所以1+sinx≠0,于是:

=右边.
所以,原式成立。
这样的讲解,似乎学生都听得“懂”,因为它步步有依据、理由充分、条理清晰。但是,这里的“懂”,其实是“假懂”。从解题的逻辑过程看,学生确实是“每步都懂了”,但在学生心理仍然存在困惑:老师怎么那么厉害,一下子就懂得在等式左边的分子和分母都乘以“1+sinx”?这个问题没有弄清楚,其实就是没有弄懂,没有学会“教材”的思考方法,今后遇见类似问题照样不会做,这是典型的假懂。
如何讲好这个例题呢?首先,必须让学生明白,所谓解题就是寻找“已知”与“欲求”之间的通道。如果从“已知”入手,就是把“已知”逐步往“欲求”转化;如果从“欲求”入手,就是把“欲求”逐步往“已知”转化。就本题的恒等式证明题而言,就是寻找一条“连接”等式两边的通道,实现“左”“右”两边的“化同”。其次,让学生明了本题的证法一实际上就是在寻找一条将“左边”化为“右边”的通道,实现从“左边”向“右边”转化:在左边的分子、分母同乘以“1+sinx”的目的正是为了在左边的分子部分“构造”一个与右边分子相同的式子,实现“局部化同”,再逐步消除两边的“差异”,完成整体的“化同”的解题目的。最后,进一步要求学生根据证法一的思想给出的其他证明方法。
证法2(局部化同——分母化同):


所以,原式成立。
证法3(整体化同——分子、分母同时化同):
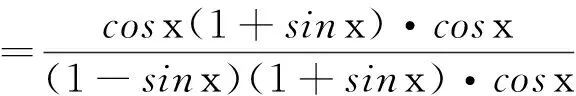


所以,原式成立。
通过这样的讲解,学生不但学会了本题的证明,而且学会了证明等式的一般方法,并将之内化为己有,用于解决其他问题。
3.挖掘习题内含的学习价值
教材的习题往往承载着巩固所学知识,深化对基本概念、原理、法则的理解,拓展学生思维和见识的功能,是帮助学生深度理解教学内容、促进学生将知识和方法内化为自身的知识结构、训练学生运用所学知识和方法分析解决问题能力的重要载体。在强调“价值引领、素养导向、能力为重、知识为基”、倡导减少“死记硬背”和“机械刷题”的背景下,教材的习题更是高考命题的重要“题源”。教学应关注对课后习题的开发与应用,拓展学生的视野,引发深刻理解数学问题的本质,实现深度学习。如,人教A版教材必修第一册第214页第19题:容易知道,正弦函数y=sinx是奇函数,正弦曲线关于原点对称,即原点是这些曲线的对称中心.除原点外,正弦曲线还有其他对称中心吗?如果有,那么对称中心的坐标是什么?另外,正弦曲线是轴对称图形吗?如果是,那么对称轴的方程是什么?你能用已经学过的正弦函数性质解释上述现象吗?对余弦函数和正切函数,讨论上述同样的问题.
它不是一道普通的习题,是对所学的正弦函数、余弦函数及正切函数图象性质的进一步总结、延伸与拓广,是帮助学生深化对这三类函数对称性理解的归纳性问题。下面给出的2022年新高考(I)卷第6题就是在本题的基础上综合正弦函数的周期性命制的。



(二)关注思维能力的培养与训练
由于新高考的数学命题强调通过创新考查思路、试题设计,以及反套路、反刷题等方式,引导改变机械死板、以练代讲的教学模式,注重用比较开放、灵活的题目,让真正理解学科内涵的学生能够发挥出自身的水平。由此,解题教学就不能光顾展示解题过程,只停留在“解法”的展示上,要重视解题思路产生过程的揭示,让学生从中学会分析解决问题。解题教学要关注解决特定问题的具体的思维方法的培养,更要关注解决问题的一般性思维原则及策略的培养与训练,引导学生自觉应用“同型原则”“就简原则”“奇正原则”等解题思维的一般性原则及“语言翻译”“结构迁移”“数形结合”“发掘隐信”“执果寻因”“特值探路”等解题思维的基本策略分析解决问题,真正提高学生分析解决新问题的能力,提升学生的核心素养。
(三)关注学科技能的培育与固化
运算是数学的童子功,推理是数学的命根子。数学运算、逻辑推理、识图作图等基本技能是学好数学的核心基础,新高考试卷也十分关注对这些核心技能的考查。而技能的形成不是一蹴而就的,是需要进行长期训练的。因此,在日常教学中要认真研究学生在基本技能方面存在的问题,明确训练目标,合理训练。在运算技能方面,要关注算理算法的揭示,让学生明算理、清算法,养成自觉依据算理算法实施运算的习惯,加强对指数和对数运算、等差和等比数列的基本运算、数列求和、三角恒等变换、解方程(组)、解不等式(组)、向量运算、求导运算以及近似计算等的合理训练。在逻辑推理方面,要让学生明了归纳推理、类比推理、演绎推理的内涵,清楚各种推理方式在解决问题中的作用,掌握它们的表达方式,并能根据解决问题的需要选择适当的推理方式表达思维结果,做到推理有据、条理清晰、表达准确。在识图作图解决代数问题时,要能根据函数的解析式作出对应图象、或由函数性质把握其图象特征作出草图,能把握函数解析式变化与其图象变换的对应关系,合理地进行数与形的转化;几何问题中,要能快速准确地作出解析几何与立体几何问题中的示意图、并根据图形得到有用的几何关系和数量关系,能准确把握平面图形的折叠及立体图形的展开,能根据需要作出几何图形的辅助线、辅助面及对已有图形进行割补;统计问题中,要能根据需要迅速作出统计图表或从统计图表中迅速获取有用信息等。
总之,新一轮的高考改革立足国家人才选拔的需要,涉及面广,改革力度大,是多方面的综合改革,对中学教学的影响将是深远的。本文仅仅依据相关文件及近两年的新高考试卷管中窥豹地谈些看法,至于更深入的问题尚待日后进一步研究。
