基于多策略花朵授粉优化的模糊聚类算法

摘  要：为解决传统FCM算法存在对初始值过度依赖问题，提出一种基于多策略改进花朵授粉算法优化的FCM算法，基于多策略改进FPA算法在初始化阶段及搜索阶段分别引入混沌映射、惯性权重因子和黄金正弦算法，使其寻优能力及速度均得到提高；最后，通过多策略改进FPA算法得到的最优解作为FCM算法的初始聚类中心进行聚类分析，从而解决传统FCM算法对初始中心敏感及陷入局部最优等问题。

關键词：多策略；混沌映射；FPA；FCM

中图分类号：TP183； 文献标识码：A  文章编号：2096-4706（2023）09-0014-04

Abstract： In order to solve the problem that the traditional FCM algorithm is excessively dependent on the initial value， an improved multi-strategy Flower Pollination Algorithm （FPA） is proposed to optimize the FCM algorithm. Based on the multi-strategy improvement of FPA algorithm， chaos mapping， inertia weighting factor and golden sine algorithm are added in the initialization phase and the search phase respectively， which improves the optimization searching ability and the speed. Finally， the FCM algorithm is used as the initial cluster center to cluster and analyze the optimal solution obtained by the multi-strategy FPA algorithm， thus solving the problems of the traditional FCM algorithm sensitive to the initial center and falling into the local optimum.

Keywords： multi-strategy; chaos mapping; FPA; FCM

0  引  言

FCM算法在数据挖掘领域里已然成为当前的研究热点，并被广泛地应用于信息检索、人工智能、图像处理等领域。但是也存在对算法的初始值过度依赖、模糊指数m和聚类数目k需人为设定等问题。目前国内外许多研究人员对该算法进行了优化改进：ZHAO等利用不动点定理和Banach压缩映射原理，提出了一种适用于使用闵可夫斯基度量作为相似性度量的模糊聚类算法，拓宽了传统模糊聚类算法的应用范围，同时也在算法的全局搜索能力和收敛速度上有了明显提升[1]。PANTULA等为提高聚类效率，将人工神经网络引入模糊聚类之中，提出了神经模糊C均值聚类算法[2]。吕冰垚等将粒子群算法与遗传算法结合进行全局搜索优化模糊聚类算法的聚类中心[3]。董发志等针对模糊聚类算法的缺陷，将遗传算法优化用于优化初始聚类中心，从而达到优化聚类的目的[4]。KUMAR等在工蜂群算法的帮助下使模糊聚类算法跳出了局部最优，利用常见的UCI数据集对改进后算法的性能进行了验证[5]。

花朵授粉算法（FPA）作为智能优化算法，具有寻优能力强、适用性强等特点[6]。但该算法存在寻优精度低、易陷入局部最优等问题，因此许多学者对该算法进行改进：陶志勇等提出了一种在全局阶段利用正态分布缩放因子和局部阶段引入变异策略优化FPA算法[7]。陆克中等提出了一种自适应变异的量子花授粉算法进行优化改善[8]。贺智明等提出了一种基于动态全局搜索指导寻优方向利用和柯西变异增加种群多样性并帮助算法跳出局部最优等问题[9]。

基于以上算法的优缺点，本文使用改进的花朵授粉优化模糊聚类算法（WGF-FCM）。该算法首先在初始化种群时，引入混沌映射来优化种群的初始位置，使得算法提高全局的搜索种群解的概率，确保种群多样性；其次使用惯性权重因子和黄金比例系数改善收敛精度以及寻优的能力，然后使用改进的花朵授粉算法优化模糊聚类算法，解决模糊聚类算法存在的问题，以此达到更好的聚类效果。

1  花朵授粉算法

花朵授粉算法通过模拟自然界花朵授粉的过程进行建模，实现花朵授粉算法主要有两个阶段：

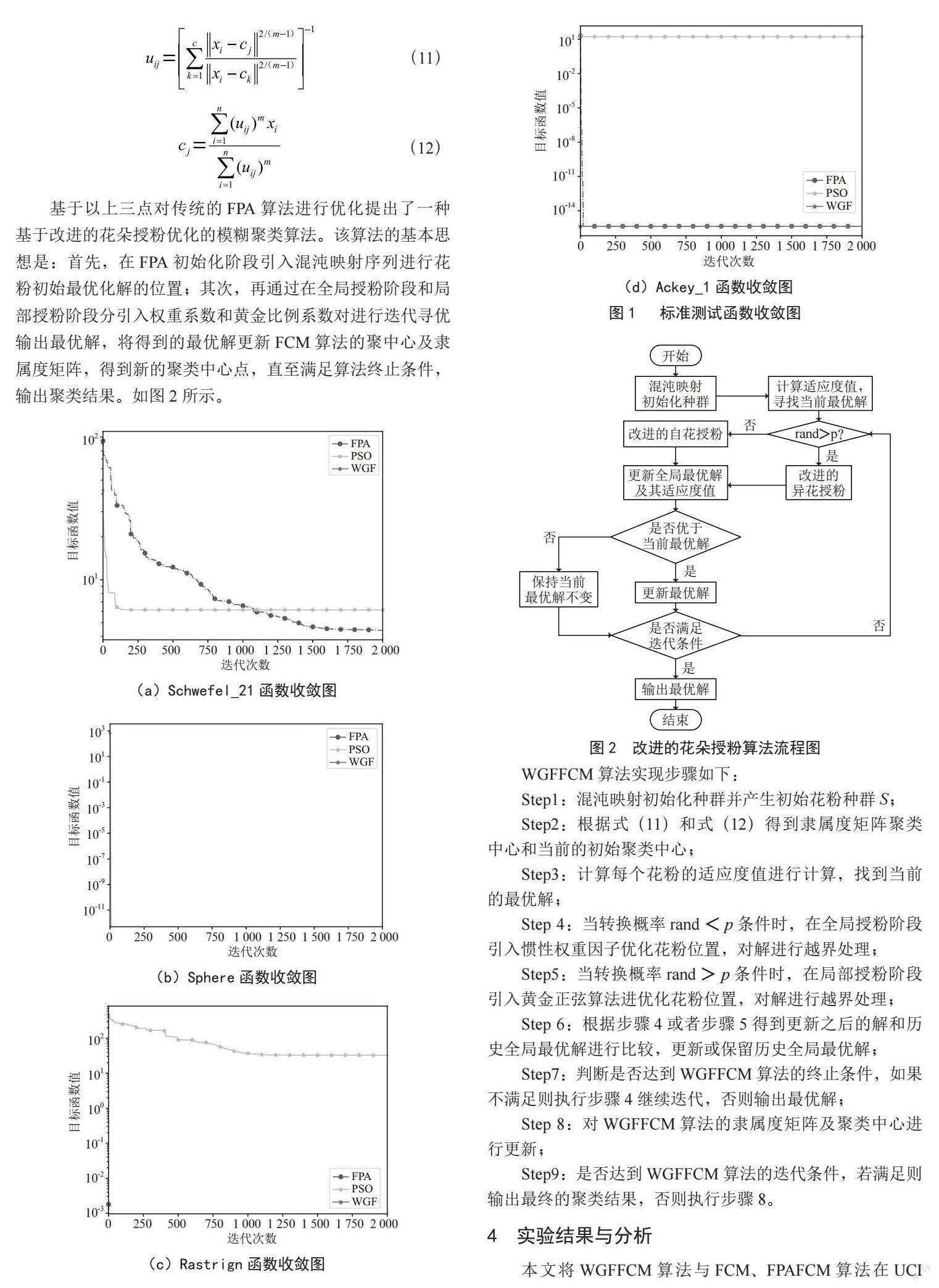
基于以上三点对传统的FPA算法进行优化提出了一种基于改进的花朵授粉优化的模糊聚类算法。该算法的基本思想是：首先，在FPA初始化阶段引入混沌映射序列进行花粉初始最优化解的位置；其次，再通过在全局授粉阶段和局部授粉阶段分引入权重系数和黄金比例系数对进行迭代寻优输出最优解，将得到的最优解更新FCM算法的聚中心及隶属度矩阵，得到新的聚类中心点，直至满足算法终止条件，输出聚类结果。如图2所示。

WGFFCM算法实现步骤如下：

Step1：混沌映射初始化种群并产生初始花粉种群S；

Step2：根据式（11）和式（12）得到隶属度矩阵聚类中心和当前的初始聚类中心；

Step3：计算每个花粉的适应度值进行计算，找到当前的最优解；

Step 4：当转换概率rand＜p条件时，在全局授粉阶段引入惯性权重因子优化花粉位置，对解进行越界处理；

Step5：当转换概率rand＞p条件时，在局部授粉阶段引入黄金正弦算法进优化花粉位置，对解进行越界处理；

Step 6：根据步骤4或者步骤5得到更新之后的解和历史全局最优解进行比较，更新或保留历史全局最优解；

Step7：判断是否达到WGFFCM算法的终止条件，如果不满足则执行步骤4继续迭代，否则输出最优解；

Step 8：对WGFFCM算法的隶属度矩阵及聚类中心进行更新；

Step9：是否達到WGFFCM算法的迭代条件，若满足则输出最终的聚类结果，否则执行步骤8。

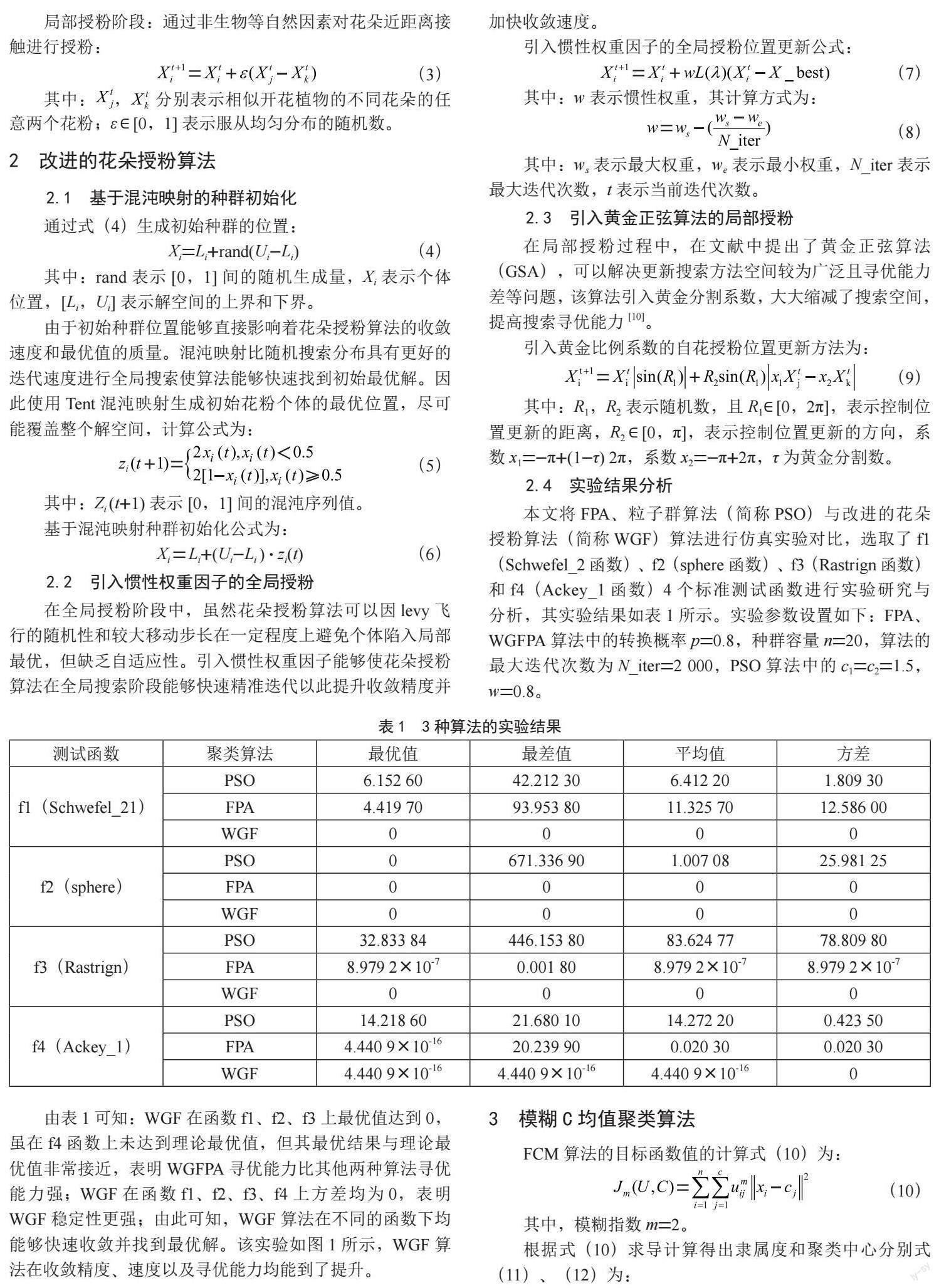
4  实验结果与分析

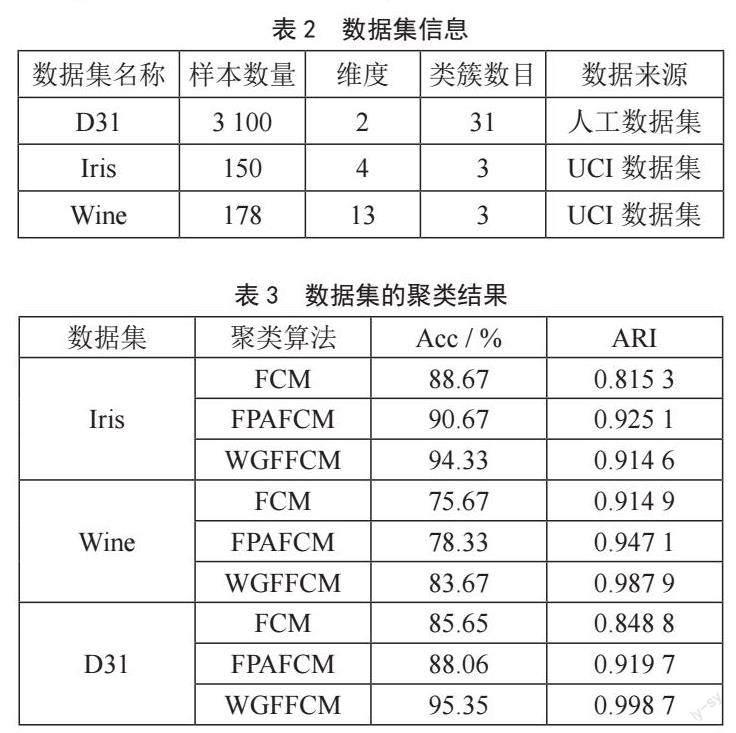
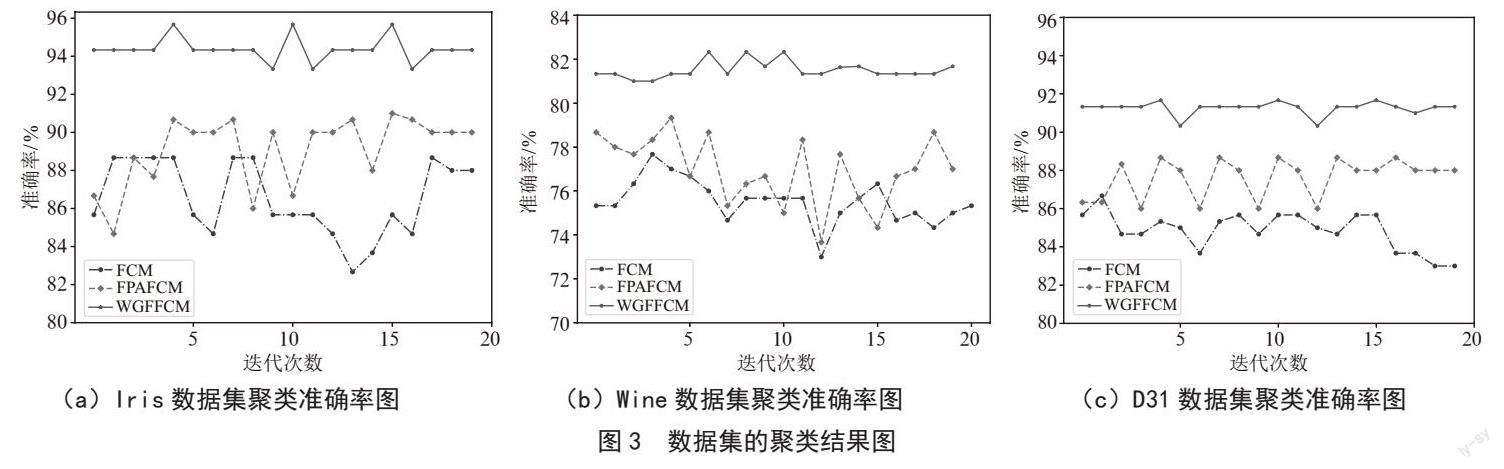
本文将WGFFCM算法与FCM、FPAFCM算法在UCI数据集上和人工数据集D31上进行实验对比，数据集信息如表2所示。实验结果如表3所示，3种算法的结果对比图如图3所示。实验参数设定如下：模糊指数m=2，种群规模n=20，迭代次数20次，Levy飞行参数λ=1.5，种群转换概率p=0.8，编程运行环境为Python 3.8。

本文分别使用ACC（准确率）和ARI（调整兰德系数）这2个聚类评价指标对WGFFCM算法的聚类效果进行比较与分析。ARI越接近1则表明聚类效果越好。分析表2中的数值可以得出，3种算法中WGFFCM算法的ACC和ARI优于另外2种算法。在数据集D31上，WGFFCM算法的ACC相比于FCM、FPAFCM分别提升了9.7%、7.29%，且ARI接近于1，表明WGFFCM算法比其他2种算法聚类效果更佳；虽然WGFFCM算法在数据集Iris中的ARI低于FPAFCM算法，图3中WGFFCM算法在3个1数据集上的ACC、ARI及稳定性优于其他2种算法。

5  结  论

本文提出的多策略优化FPA算法使得WGFFCM算法快速找到最优的初始聚类中心，提高了模糊聚类的聚类准确率以及聚类效果。仿真实验结果证明：WGFFCM算法相较于FCM、FPAFCM算法，在聚类效果、稳定性及聚类准确率均得到了显著提升。

参考文献：

[1] ZHAO K X，DAI Y P，JIA Z Y，et al. General Fuzzy C-Means Clustering Algorithm Using Minkowski Metric [J].Signal Processing，2021，188：108161.

[2] PANTULA P D，MIRIYALA S S，MITRA K. An Evolutionary Neuro-Fuzzy C-Means Clustering Technique [J].Engineering Applications of Artificial Intelligence，2020，89（C）：103435-103435.

[3] 吕冰垚，姜志翱，宁春玉.基于PSO和GA混合优化的FCM算法 [J].长春理工大学学报：自然科学版，2021，44（6）：125-130.

[4] 董发志，丁洪伟，杨志军，等.基于遗传算法和模糊C均值聚类的WSN分簇路由算法 [J].计算机应用，2019，39（8）：2359-2365.

[5] KUMAR A，KUMAR D，JARIAL S K. A Hybrid Clustering Method Based on Improved Artificial Bee Colony and Fuzzy C-Means Algorithm [J].International Journal of Artificial Intelligence，2017，15（2）：40-60.

[6] 高翻翻，丁正生.融合动态收敛因子与黄金正弦的花朵授粉算法 [J].河南科技大学学报：自然科学版，2022，43（2）：47-53+7.

[7] 陶志勇，崔新新.混合改进的花朵授粉算法 [J].传感器与微系统，2019，38（10）：139-142+145.

[8] 陆克中，章哲庆，刘利斌.自适应变异的量子花授粉算法 [J].控制工程，2020，27（4）：683-691.

[9] 贺智明，李文静.基于动态全局搜索和柯西变异的花授粉算法 [J].计算机工程与应用，2019，55（19）：74-80+222.

[10] TANYILDIZI E，DEMIR G. Golden Sine Algorithm：A Novel Math-Inspired Algorithm [J].Advances in Electrical and Computer Engineering，2017，17（2）：71-78.

作者简介：吴晴（1997—），女，汉族，河南商丘人，硕士研究生在读，研究方向：模式识别与人工智能。