弯曲套损井整形修复中的打孔割缝应力释放研究

2023-06-18常方瑞李汝强李发禄韩晓强曹小建李玉坤刘建林李瑞勇

油气田地面工程 2023年6期

关键词：内压内壁屈服

常方瑞李汝强李发禄韩晓强曹小建李玉坤刘建林李瑞勇

1中国石化胜利油田分公司油气井下作业中心

2中国石化胜利油田分公司工程技术管理中心

3青海油田井下作业公司

4中国石油大学（华东）储运与建筑工程学院

套管是油井的重要组成部分，一旦损坏，将造成很大的经济损失。国内外的很多油水井都存在严重的套管损坏现象，严重时使得油田产量下降甚至直接导致油水井报废[1-3]，加大井筒问题修复力度刻不容缓。套管损坏主要包括四种类型：套管破漏、套管缩径、套管弯曲和套管错断[4-5]。截至到2020年6月，胜利油田在册套损井4941口，其中弯曲套损井1268口，占25.7%。在美国墨西哥湾、加利福尼亚、南美洲及亚洲等地区，部分油田出现套管损坏现象，主要原因有不同地层之间的相对运动引起套管变形、挤压乃至错断。在过去的20 年里，美国贝尔利吉油田发现了1000 多口套损井已经有明显的地层压实、井筒损坏，表现为轴向挤压、剪切和塌陷，注水作业后能够有所缓解，但是也严重影响了该油田的稳高产。开发不到10 年的美国威明顿油田，套管失效井占到总井数的41%。套管损坏已是世界各大油田面临的问题[6]。

国外套管弯曲治理主要以套管补贴和侧钻打通道为主，斯伦贝谢、哈里伯顿、威德福等油服公司采取可膨胀悬挂系统快速完成对套管损坏的治理；针对套管无通径的弯曲井，采取侧钻打通道的方法，如威德福公司的Quick cut 开窗系统，实现高效治理套损井[7]。国内大庆油田套管弯曲治理主要有无通道套弯井修复技术和膨胀管密封加固技术，形成了纵向磨铣、逆向锻铣和自下而上、自上而下的膨胀管技术等，实现了对套管弯曲的有效治理[8]。辽河油田套管弯曲治理以打通道技术为主，形成了领眼示踪修套、满眼扶正修套和整形修套三种高效打通道技术，能有效治理稠油生产过程中高温注气、火烧油层导致的套管弯曲问题。国内还有一些其他套损井治理技术，包括LEP长效隔水采油技术[9]、套管补贴技术[10-11]、化学堵漏技术等。

胜利油田针对套管缩径、破漏、错断井，形成了系列成熟技术，对弯曲不严重的套损井的治理采用整形修复的方式，技术难点在于地应力没有得到释放，存在回弹现象，影响治理成功率。本研究拟以孤岛某弯曲套管为研究对象，通过水射流轴向切割技术，对弯曲套管进行应力释放、通道恢复等修复技术，确保形成直井通道。水射流切割可采用打孔或者切割成缝等多种切割方式。对打孔和割缝两种应力释放方式进行有限元仿真分析，探究打孔和割缝两种方式分别对弯曲管段结构强度的影响，用来表征对结构应力释放的程度。

1 弯曲套管模型及应力释放计算

以孤岛某弯曲套管为研究对象，弯曲的套管如图1所示。截取一段弯曲管道建立三维实体模型进行打孔和割缝的应力释放研究。有限元模型的长度为1 m，外径177.8 mm、内径159.42 mm、壁厚9.19 mm。材料采用N 80 钢，该材料的屈服极限为760 MPa，当应力超过该极限时材料屈服，材料屈服之后的塑性切线模量为6 100 MPa。本研究以使结构屈服时所需施加载荷的大小为结构屈服强度，用其来衡量结构的强度。

图1 孤岛中19-5井套管弯曲变形Fig.1 Bending deformation of the casing pipe of No.19-5 Well in Gudao

分别采用在井筒壁面打孔和割缝两种形式对弯曲套管进行应力释放研究。其中，打孔方式为在每个环面上打3 个孔，分别建立了打3、6、9、12、15孔等模型，且孔径分别设置了6、8、10 mm三种数值。综上所述，打孔方式一共有15个模型。图2选取了孔径为6 mm 的3 个孔和15 个孔模型进行展示。

图2 孔径为6 mm的不同打孔数模型Fig.2 Models of 6 mm aperture with different numbers of holes

割缝方式分别选取了缝宽6、8、10 mm三个数值，每个不同缝宽的模型在环向分别割置了1 条缝、2 条缝、3 条缝、4 条缝。割缝方式一共有12个模型。图3选取了直径为6 mm的管段割1条缝和4条缝的模型展示。

图3 直径为6 mm的不同割缝数模型Fig.3 Models of 6 mm diameter with different numbers of slits

不同割缝和不同打孔模型的屈服强度不同，原始管道（未割缝，未打孔）模型在内壁受80.70 MPa 压力时，其结构最大应力值达到屈服极限760 MPa。

套损井管道一般为轴对称结构，而且距离比较长，可对管道的受内压状态建立平面应变模型。对于圆管、圆柱类的轴对称问题，构件的几何形状和外载荷都不随极角变化，应力分布与极角无关，且剪应力等于零，应力函数仅是矢径的函数。此类结构一般采用极坐标，如图4所示。

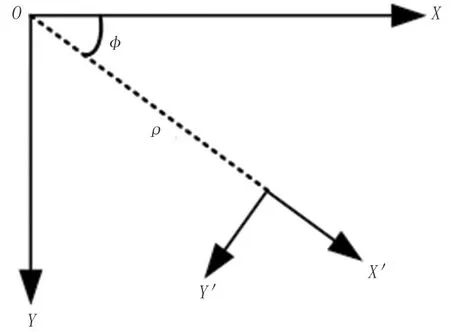
图4 极坐标Fig.4 Polar coordinates

图中，ρ为半径，m，φ为角度，°。极坐标中的应力分量用应力函数Φ表示之后，得到平面应变状态下应力双调和函数[9]：

式中：A、B、C、D为任意系数。

将式（2）代入式（1）可得应力分量为

式中：σρ为径向正应力，MPa；σφ为环向正应力，MPa；τρφ为剪应力，MPa。

解得应变分量为

式中：ερ为径向正应变；εφ为环向正应变；γρφ为切应变；E为材料弹性模量，MPa。

对于受均匀分布内压的薄壁管道，进行应力与位移变形分析。设圆管内半径为a，单位m；外半径为b，单位m；受内压p，单位Pa（图5）。

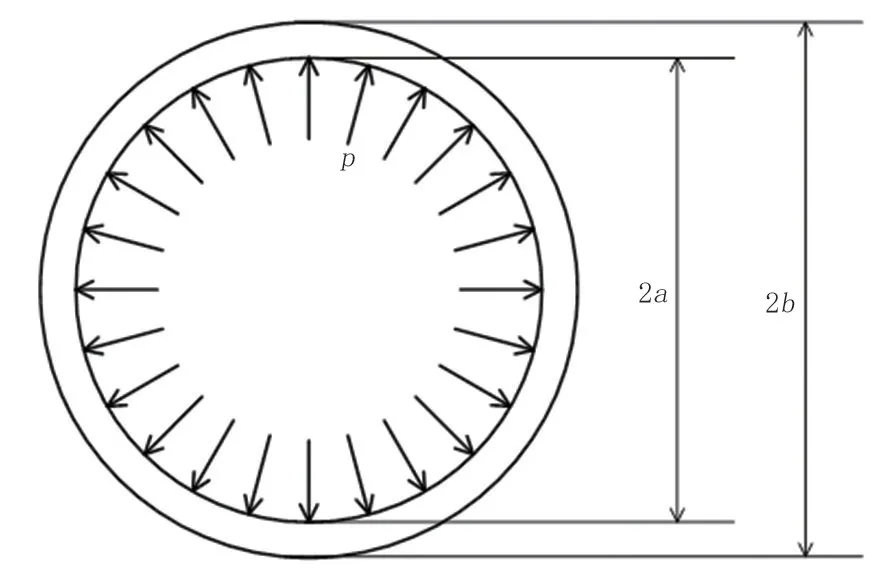
图5 薄壁圆管受均布内压示意图Fig.5 Schematic diagram of the thin-walled circular tube under uniformly distributed internal pressure

应力分布呈轴对称分布，则应力分量可表示为

依据边界条件，管内壁受压p，则有

将式（6）代入应力表达式（5），可以得到

根据位移单值条件，B=0[9]。

将A、B、C代回应力分量表达式（5），最终得到

对于长输油气管道，求解分析管道应力可以简化为平面应变问题，根据空间轴对称问题物理方程的极坐标表示，其中沿管道轴向的应变表达式为

式中：μ为材料泊松比；εz为轴向正应变；σz为轨向正应力，MPa。将式（8）代入式（9），求解得到管道轴向应力为

由式（8）和式（10）可知，管道应力与管道内部压力p成正比。取ρ=D/2，即公称直径，壁厚t=b-a，m；则轴向应力和环向应力可表示为

该研究采用平面应变模型后，弯曲套管受内压后的应力解析解形式即为式（11）。

2 强度分析

2.1 不同打孔模型的强度分析

对弯曲套管需要进行应力释放，以方便对其进行修复整形，一般采用对弯曲套管打孔或者割缝方式进行应力释放。为给井下作业提供理论参考，现对管段设置多种不同的打孔和割缝模型，采用有限元仿真软件ANSYS 计算不同的打孔或者割缝形式对结构强度的降低程度。

图6 展示孔径为10 mm、不同打孔模型屈服时的Mises应力结果。

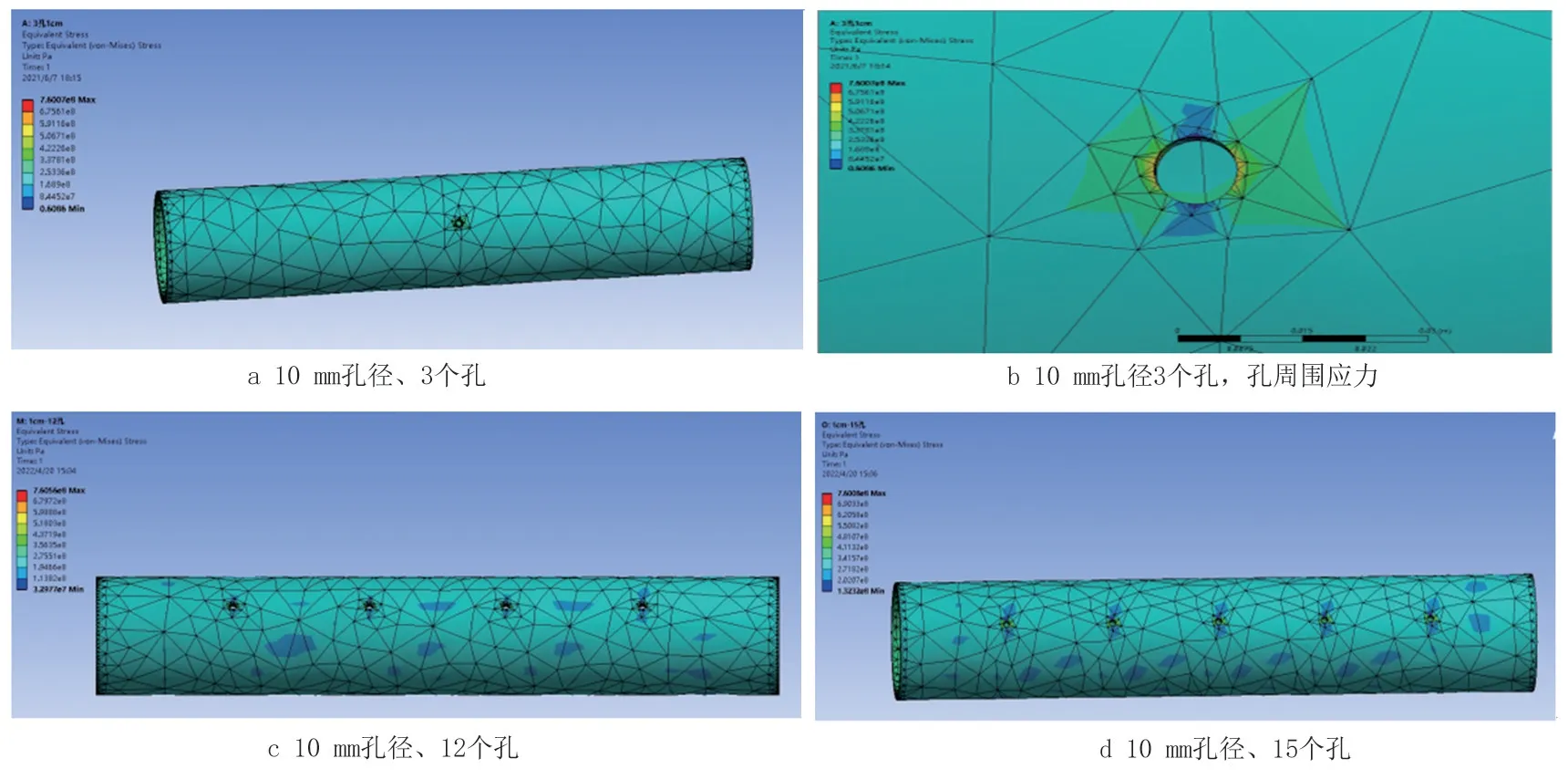
图6 10 mm孔径、不同孔数结构屈服时Mises应力结果Fig.6 Mises stress results of the pipes with 10 mm aperture and different numbers of holes at yield

2.2 不同割缝模型的强度分析

对弯曲管进行割缝处理时，分别建立了缝宽为6、8、10 mm，且每个缝宽分别割1、2、3、4条缝的不同模型。对10 mm缝宽、不同割缝数结构屈服时的应力结果进行展示（图7）。

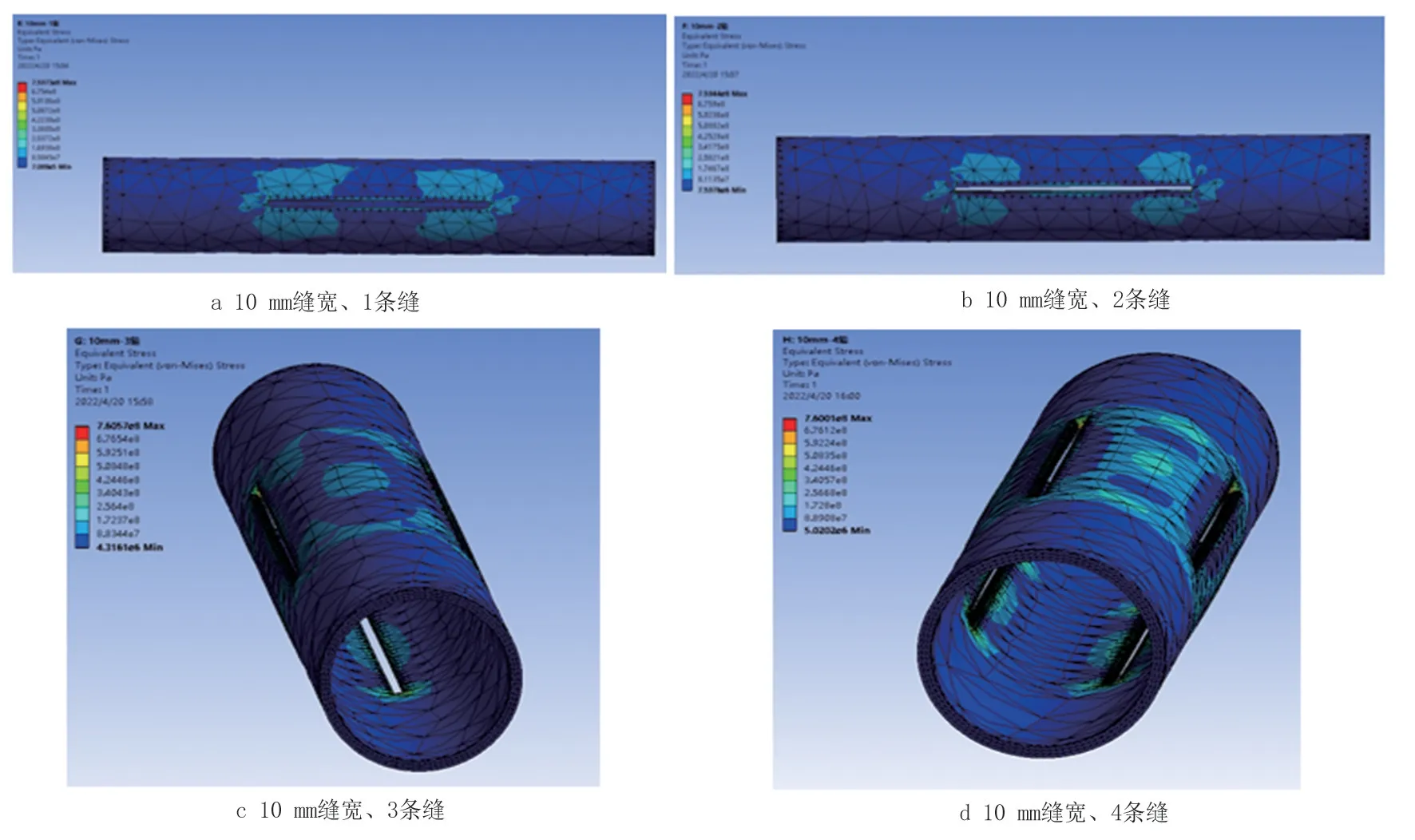
图7 10 mm缝宽、不同割缝数结构屈服时Mises应力结果Fig.7 Mises stress results of the pipes with 10 mm slit width and different numbers of slits at yield

3 打孔、割缝对应力释放的影响规律

将打孔应力释放模型中不同孔径、不同打孔数结构屈服时所需给管道内壁施加的内压结果汇总（表1），绘制成曲线如图8所示。

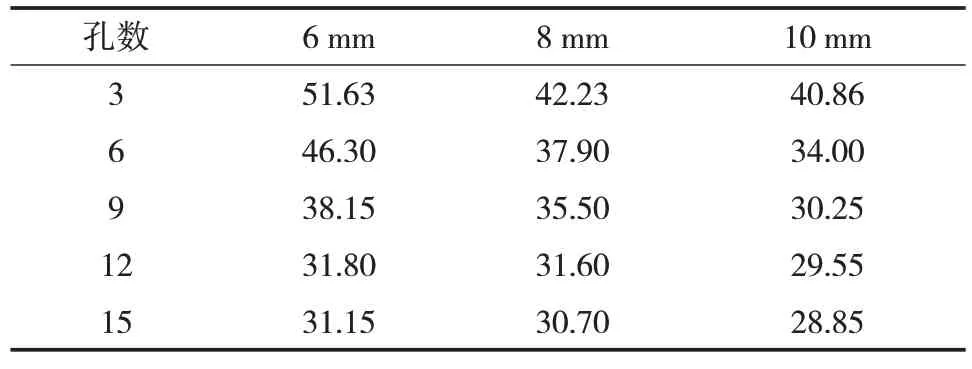
表1 不同孔径、不同打孔数结构屈服时管内壁所需内压Tab.1 Internal pressure required for yield on the inner wall of the pipe with different apertures and different numbers of holes MPa

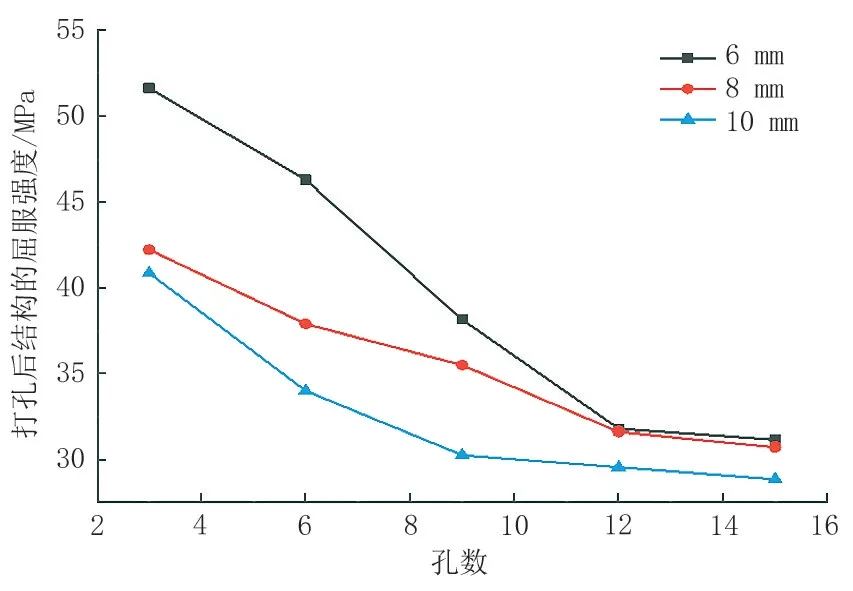
图8 不同孔径、不同打孔数结构屈服时管内壁所需内压Fig.8 Internal pressure required for yield on the inner wall of the pipe with different apertures and different numbers of holes

由表1 和图8 可知，打孔方式对结构的强度有着显著影响。打孔个数越多，结构屈服强度降低越多；打孔孔径越大，结构屈服强度降低越多。当打孔数为3时，结构屈服时管内壁所需内压由原始未打孔弯管的80 MPa 下降至51.63 MPa，此时结构强度下降至原始的64.0%，结构强度削弱了36%。当打孔数为12 甚至更多时，打孔方式对结构强度的削弱强度减弱，当孔数从12 增加到15 时，结构强度只在12 个孔的基础上削弱了0.65 MPa。由此可见，采用打孔方式对结构的强度削弱很明显，但当打孔数增加到12 之后，对结构强度的削弱强度在减弱。综上所述，针对1 m长的弯曲管段，打孔数为6 个或者9 个时效果最佳，对结构的应力释放效率最高。

将不同缝宽、不同割缝数结构屈服时管内壁所需内压结果汇总（表2），绘制成曲线如图9所示。

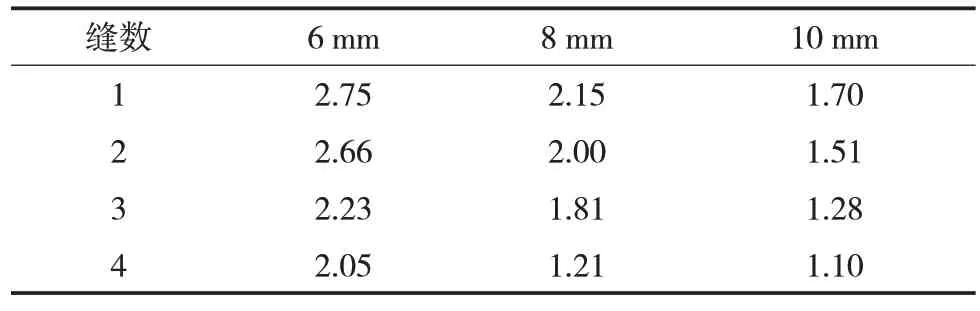
表2 不同缝宽、不同割缝数结构屈服时管内壁所需内压Tab.2 Internal pressure required for yield on the inner wall of the pipe with different slit widths and different numbers of slits MPa

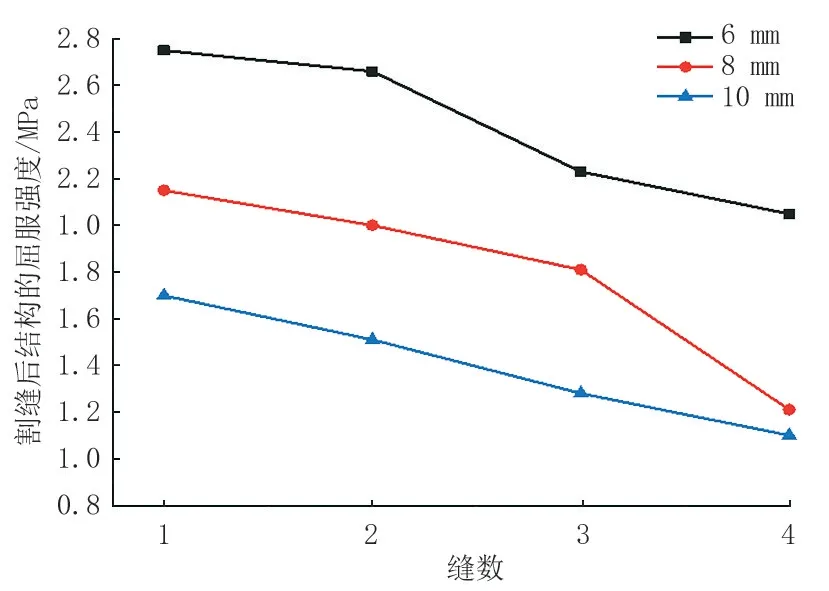
图9 不同缝宽、不同割缝数结构屈服时管内壁所需内压Fig.9 Internal pressure required for yield on the inner wall of the pipe with different slit widths and different numbers of slits

由表2 和图9 可知，射孔和割缝后的结构强度明显降低孔径越大，结构强度降低更多；孔数越多，结构强度降低也越多；割缝的缝越宽，结构强度降低更多；缝数越多，结构强度降低也更多。割1条缝，缝宽为6 mm时，结构达到屈服对管内壁所需施加的内压由原始未打孔或割缝模型的80.70 MPa 直接降低到2.75 MPa。由此可见，割缝对结构的应力释放和强度削弱非常显著，相比于打孔形式，割缝可宽泛理解为打了一排连续的孔洞形成的一条缝。因此，割缝形式对结构强度的削弱程度比打孔形式的效果显著。

在许多工程结构中，孔口、孔边的应力将远大于无孔时的应力，也远大于距孔稍远处的应力，这种现象称为孔边应力集中。射孔和割缝后结构应力得到释放，结构强度显著降低，可由应力集中现象来解释。应力集中是指结构或构件局部区域的最大应力值比平均应力值高的现象。一般是由于截面急剧变化应力局部增大，尖角、孔洞、槽孔、缺口等处容易出现应力集中。应力集中系数α，它是峰值应力和不考虑应力集中时的应力（即名义应力）的比值，且恒大于1。与物体的几何形状和加载方式等因素有关，与载荷的大小无关。α表达式为：

式中：σ为平均应力，MPa。

打孔及割缝两种应力释放方式造成的结构强度降低，可采用应力集中系数定量化将降低的强度部分折算入应力计算。

当打孔数为3时，结构屈服时管内壁所需内压由原始未打孔弯管的80.70 MPa 下降至51.63 MPa，此时，可将孔附近的应力集中系数等效换算为80.70/51.63=1.56。其他打孔或者割缝模型的等效应力集中系数可依此类推。