海洋湍流外尺度对高斯光束传输特性的影响

杨祎，聂欢，王晓波，张建磊，和晗昱，邱晓芬，朱云周

（1 西安邮电大学 电子工程学院，西安 710121）

（2 中国船舶集团公司 第705 研究所，水下信息与控制重点实验室，西安 710077）

0 引言

水下激光通信克服了水下电磁波通信、水声通信的一些缺陷，可以实现大数据容量、高数据速率的信息传输。真实的海水环境对传输光信号的影响是光的吸收散射和湍流效应等因素的综合作用［1］。吸收效应取决于水的折射率［2］，散射效应基于米氏散射理论通过散射相函数（Henyey Greenstein，HG）描述［3］。基于蒙特卡洛法可对水下无线光通信（Underwater Wireless Optical Communication，UWOC）系统吸收、散射信道的传输特性进行研究［4-5］。湍流效应通常基于湍流折射率功率谱模型研究，海洋湍流折射率功率谱是海水折射率在一定空间尺度上的随机起伏造成的，折射率的波动受到温度和盐度波动的共同控制［6］。

相位屏法通常用于湍流信道建模，2017年赵生妹等［7］使用功率谱反演法验证了海洋湍流相位屏模型的有效性。针对功率谱反演法生成的随机相位屏低频分量不足的缺陷，潘孙翔等［8］用次谐波补偿法对相位屏进行了改进。牛超君等［9］使用相位屏法仿真了不同海洋湍流参数下光的传输特性，与理论计算结果进行了对比。2021年王新光等［10］证明了基于海洋湍流随机相位屏模型的仿真方法是一种直观、方便的方法，可通过理论推导或者实验来研究光在海洋湍流中的传播特性。因为功率谱反演法产生相位屏的核心在于海洋湍流功率谱模型，目前，通过功率谱反演法生成的海洋湍流相位屏的仿真［9］并没有考虑外尺度对于光学特性的影响，根据Richardson 的能量级联理论［11］，湍流的能量注入之后，以外尺度和内尺度为界的湍流区域形成了惯性子区，能量从外部注入后经过惯性子区转移，最终进入到耗散区耗散完毕，因而描述整个湍流区域折射率变化的功率谱应满足能量的收敛。三种最常用的外部尺度模型分别是指数模型（Exp）、冯·卡曼模型（Von Karman，VK）和格林伍德模型（Green Wood，GW）。陆璐［12］利用合流超几何函数的性质推导了海洋湍流中传输的平面波和球面波基于Nikishov 海洋湍流折射率谱的波结构函数和空间相干长度的数学表达式，为后续Nikishov 修正谱模型的光学参量表达式推导提供了思路。因指数型外尺度模型便于分离变量，使得基于Nikishov 谱的指数型外尺度修正谱成为相对容易处理的谱模型。近来也有学者相继提出了包含外尺度的新型海洋湍流折射率功率谱模型，栾晓晖等［13］基于Von Karman 模型通过添加修正因子(κ2+κ022)-11/6将Yao 谱［14］扩展为一个包含外尺度参数的新型海洋湍流折射率谱模型，从理论上分析了高斯光束在弱海洋湍流中传输时的光束漂移方差；同时间段李烨等［15］也基于Von Karman 模型提出了一个包含外尺度参数的新型海洋湍流折射率谱模型，推导了高斯光束闪烁指数的解析表达式。新型海洋湍流折射率谱模型均通过简化参量δ=8.284(κη)(4/3)+12.978(κη)2计算的复杂性，将指数的参数变为单项式，但是该简化在光学参量的计算中优势并不是绝对的，在积分变量g(κ)Φn(κ)中，若g(κ)包含κ4/3的e 指数次方，则依旧需要计算参量g(κ)Φn(κ)，同时新型谱的表达式相比于Nikishov 谱更为复杂，特别在针对海洋湍流中的光传输理论研究，绝大部分依旧采用标量谱线性组合形式的Nikishov 功率谱模型。同时此前的研究多为单方面对吸收、散射或者湍流的研究，2020年，张建磊等［16］通过扩展多相位屏模型建立了复合信道模型，首次将吸收散射和湍流效应统一到蒙特卡洛仿真框架中，使得综合分析衰减和湍流对通信系统的影响成为现实，但是该模型未包含海洋湍流的外尺度参数。

因此本文首先分析湍流参量外尺度引入的必要性，提出了包含外尺度参量的Nikishov 海洋湍流功率谱修正模型，分析外尺度对海洋湍流折射率功率谱及标准化光谱的影响；考虑海水吸收、散射和湍流的共同作用，使用基于相位屏的蒙特卡洛仿真方法，在指数型功率谱模型下，研究了外尺度对接收光强的概率密度函数的影响，通过波动理论和相位屏法仿真分别分析海洋湍流中外尺度对高斯光束光学特性的影响，以及湍流外尺度对信号时域扩展特性的影响。

1 基本原理

1.1 外尺度修正的海洋湍流功率谱模型

海洋湍流中折射率的波动受温度和盐度波动两个标量共同控制，Nikishov 将折射率起伏标量谱表示为温度、盐度和温盐耦合项的线性组合［17］，即

式中，κ为空间频率，A、B为折射率随温度和盐度变化的线性系数；C0=0.7，ε为动能耗散率，C1=2.35，η为内尺度，δ=8.284(κη)4/3+12.978(κη)2，AT=1.863×10-2，AS=1.9×10-4，ATS=9.41×10-3，εT=KT(dT0/dz)2，εS=KS(dS0/dz)2，εTS=，z 为海水的垂直坐标，T0为与位置相关的温度量，S0为与位置相关的温度量，KT、KS为湍流温度、盐度扩散系数。

En(κ)进一步表示为［17］

但是Nikishov 谱没有考虑海洋湍流外尺度对光学特性的影响。已有的大气湍流外尺度模型为指数型和Green Wood(κ2+κκ03)-11/6外尺度模型［11］，其中κ01=4π/L0，κ02=4π/2.04L0，κ03=4π/1.88L0。将三种外尺度模型作用于Nikishov 海洋湍流折射率功率谱，得到三种外尺度模型下的Nikishov 湍流折射率功率谱的修正谱，图1 为不同外尺度模型下的海洋湍流折射率功率谱的修正谱随κ的变化关系。不难得出外尺度趋向于无穷大时，三种外尺度模型均趋近于−11/3 幂律，即与未引入外尺度模型的Nikishov 谱相比较，三种外尺度模型均只改变功率谱的低频区域，VK 模型在低频区域完全趋近于一常数，Exp 指数模型和GW 模型比较接近，对低频区域均存在缓变地收敛限制，因此三种外尺度模型均满足了对能量注入范围的限制，使得功率谱整体具备一定的收敛性。

图1 三种外尺度模型下的Nikishov 湍流折射率功率谱的修正谱Fig.1 Modified spectra of Nikishov turbulence refractive index power spectra under three outer scale models

因为指数形式的外尺度模型便于分离参量［18］，在后续的研究中通过合流超几何函数推导光学特性的理论解析公式时，外尺度可分解为1 和e 指数之和，因此基于指数型Nikishov 谱的修正谱的光学特性解析公式可表示为基于Nikishov 谱的解析公式［19］与指数项部分的解析公式之和，两项的区别在于κ2项的系数不同，使得指数型Nikishov 谱的修正谱成为相对容易处理的谱模型。因此在后面的理论分析和仿真中均采用指数型Nikishov 谱的修正谱Φn(κ)，即

指数型Nikishov 谱的修正谱Φn(κ)对应的折射率起伏标准化光谱fn(κ)［6］表示为fn(κ)=ε-n1ε1/3κ5/3En(κ)，折射率波动的标准化光谱fn(κ)与外尺度的关系如图2。

图2 折射率波动的标准化光谱与外尺度的关系Fig.2 The relationship between the standardized spectrum of refractive index fluctuations and the outer scale

图2 为无外尺度限制Nikishov 和指数型外尺度分别2 m、1 m 时折射率波动分布的标准化光谱图，可以得出：外尺度模型只改变功率谱模型的低频区域；在没有外尺度限制即外尺度无穷大时，空间频率κ越小，惯性对流区的fn(κ)越趋近于常数C0；在指数型外尺度限制下，受有限外尺度的影响，空间频率κ越小，惯性对流区的fn(κ)越趋近于0，即整体标量谱具备一定的限制收敛性；在粘性对流区的一定空间频率范围内，外尺度越大，fn(κ)越大；外尺度不改变粘性扩散区域的折射率波动的标准化光谱。

1.2 基于相位屏的海水信道建模

利用蒙特卡洛方法对基于功率谱反演法模拟的相位屏的海水信道进行建模，使用的谱模型为指数型Nikishov 谱的修正谱Φn(κ)，信道模型示意图如图3。

图3 海水信道物理及等效的相位屏模型Fig.3 Phase screen model of seawater channel physics and equivalents

该信道模型可以同时分析吸收散射和湍流效应对水下信道光传输特性的影响，更加真实地模拟海水信道。在该信道模型下，吸收散射系数为0 时，该模型即简化为仅受湍流影响的相位屏模型；吸收散射系数不为0 时，即为受到衰减和湍流效应的复合信道模型。基于该海水信道模型，可以分析光束在水下传输时由于衰减、湍流引起的时间展宽效应以及光斑空间扩展现象。其中散射效应通过散射相函数描述，在弱湍流区域，传输距离较近时湍流对光束的影响近似可认为是纯相位扰动，因此湍流效应可通过仿真生成满足湍流理论统计特性的随机相位屏描述［20］。相位屏之间湍流造成的相位扰动φ(x，y)［20］由功率谱反演法获得，即

式中，Δx、Δy表示空域内取样间隔，x=mΔx，y=mΔy；Δκx、Δκy表示波数域内空间频域取样间隔，κx=m′Δκx，κy=n′Δκy，其中m′、n′为整数；对均值为0，方差为1 的高斯随机数进行快速傅里叶变换得到a(κx，κy)；常数为与传播方向垂直的任意薄层切片上的海洋湍流折射率变化引起的湍流相位功率谱，表示为［21］

其中Φn(κx，κy)为指数型Nikishov 谱的修正谱。传输路径上的相位屏之间相互独立，即相位屏间距Δz大于湍流的尺度。因为功率谱反演法生成的相位屏存在低频信息不足的缺陷，需要对低频次的谐波通过插值拟合的方法进行重采样，生成更符合统计特征的相位屏。相位结构函数可用来描述随机相位屏的统计特性。通过仿真生成满足湍流理论统计特性的随机相位屏，其结构函数［21］可通过对屏上两点之间的相位差进行系综平均得到，表示为

式中，<>表示系综平均，φ是相位屏系数矩阵，φ(r)表示r点的相位大小，r和r′为相位屏上不同的两个点。在次谐波补偿方式下，参考补偿阶数取值方式［21］，分析了不同的补偿阶数p=1、3、5 时相位结构函数与距离变量的关系。结果如图4 所示。

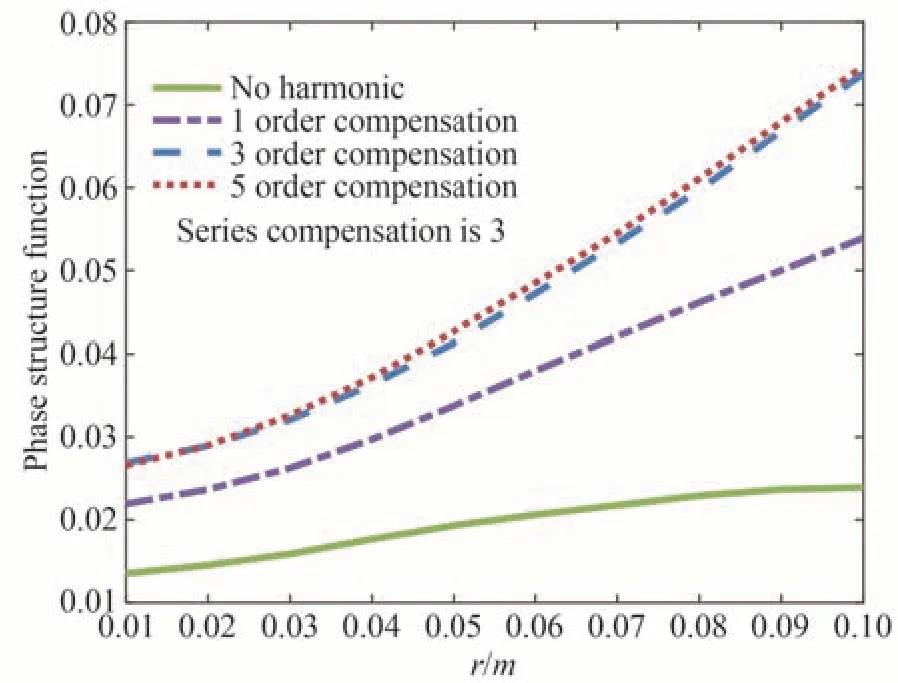
图4 不同的补偿阶数下的相位结构函数Fig.4 Phase structure function under different compensation orders

随着补偿阶数的增加，p=3 的补偿效果明显优于p=1，但是当p>3 时，继续增大补偿阶数，补偿效果提升微弱，并且增大补偿阶数会降低计算机的运算效率，占用更多的内存，因此采用低频次谐波补偿阶数p=3。

图5（a）、（b）分别为无谐波补偿和3 次谐波补偿阶数下功率谱反演法生成湍流相位屏，因功率谱反演法得到的随机相位屏有丰富的高频分量但缺少低频分量如图5（a），仿真得到的湍流相位屏每个格点之间相位变化较为明显，有丰富的高频分量，但是相位平面高度平均，说明缺少低频分量；通过补偿次谐波分量后，生成的湍流相位屏每个格点之间相位变化明显且相位屏高度发生明显倾斜，如图5（b）所示，即通过次谐波补偿的方法生成的相位屏同时具有低频分量和高频分量。

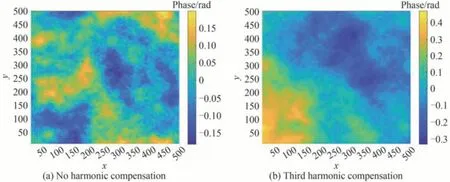
图5 功率谱反演法无谐波及三次谐波补偿生成的湍流相位屏Fig.5 Turbulent phase screen generated by power spectrum inversion method without harmonics and third harmonic compensation

1.3 湍流信道下光强的概率密度函数分布

根据已有理论：在弱湍流条件下，海洋湍流引起的接收端光强的概率密度分布函数（Probability Density Function，PDF）应服从对数正态分布［16］，即是闪烁指数，弱湍流条件下闪烁指数σ2I(L)小于1，接收到的光强度I由平均光强度I0归一化，本文通过对湍流相位屏模型进行多次蒙特卡洛仿真得到了接收光强度的PDF 分布。图6（a）为不同传输距离下相位屏仿真结果的PDF 拟合曲线。根据仿真结果可知，外尺度L0=2.5 m 时，相比于20 m 传输距离的PDF，40 m 的PDF 分布更为发散，σ2I(L=40 m)=0.0875，σ2I(L=30 m)=0.0484，σ2I(L=20 m)=0.0197，说明传输距离影响光强的概率密度分布。因为在一定的传输距离内，传输距离越长，湍流效应对接收光强的影响越大，同时对数正态分布的拟合验证了湍流相位屏模型的蒙特卡洛方法仿真海洋湍流信道特性的有效性。

图6 不同传输距离及外尺度下的PDF 曲线Fig.6 PDF curves at different transmission distances and outer scales

图6（b）为不同传输距离和外尺度下PDF 的对数正态分布拟合曲线，传输为40 m 时，2.5 m 和5 m 外尺度对应的闪烁指数分别为0.087 5、0.088 2；传输为30 m 时，2.5 m 和5 m 外尺度对应的闪烁指数分别为0.048 4、0.050 6，说明外尺度在较小程度上决定光强的概率密度分布，主要影响光强概率密度分布的是传输距离。

2 湍流信道下信号特性仿真分析

2.1 海洋湍流下的光学特性

湍流效应会引起光束漂移、光束扩展和光强起伏等现象，从而严重影响光通信系统的性能。其中光束漂移表示为［20］

高斯光束在海洋湍流环境传输时长期光束扩展表示为［20］

高斯光束在海洋湍流环境传输时轴上闪烁指数表示为［22］

2.2 湍流信道下光学特性仿真分析

仿真时采用的参数为：光子追踪数目106个，基模高斯光源波束半径1 cm，波长为532 nm，海洋湍流参量动能耗散率ε=10-6，温度方差耗散率εT=10-8，湍流内尺度η=10-3m，温度诱导与盐度诱导的比值ω=−2，次谐波补偿次数p=3，相位屏之间的间隔Δz=5 m，相位屏宽D=0.1 m，网格大小N为500×500。

将指数型Nikishov 谱的修正谱Φn(κ)代入式（8）～（10），通过数值计算光束漂移、长期波束扩展、轴上闪烁指数随距离的变化，结果分别如图7（a）、8（a）、9（a）。

图7 不同外尺度下质心漂移随传输距离的关系Fig.7 Relationship between centroid drift and transmission distance under different outer scales

图8 不同外尺度下光束扩展随传输距离的关系Fig.8 Relationship between beam expansion and transmission distance under different outer scales

接收到的光束质心(xc，yc)坐标，光斑质心的偏移程度通过质心漂移标准差衡量［9］，即

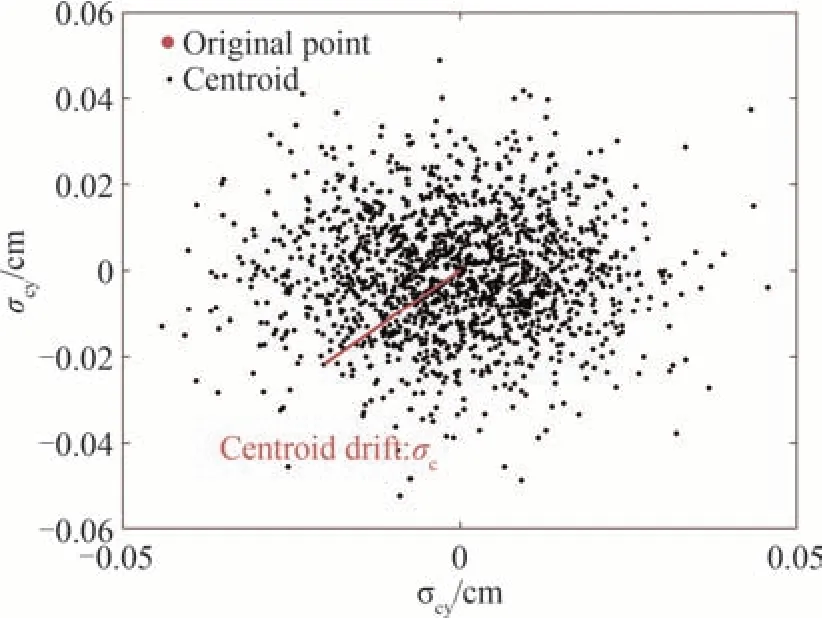
图10 质心位置分布Fig.10 Centroid location distribution map

通过多次仿真，统计接收平面轴心处接收到的光强，根据高斯光束的轴上闪烁指数表示σ2I(0，L)=，得到不同外尺度下轴上闪烁指数随传输距离的仿真结果如图9（b）。

传输距离增大，湍流效应对光学特性的影响增大，体现在光束漂移、光束扩展和闪烁指数上如图7、～9。通过对比理论计算与仿真结果可以得出：理论计算结果与相位屏仿真结果一致，验证了相位屏仿真模型的正确性。但是通过相位屏仿真外尺度对光学特性的影响时，因为相位屏生成的随机性不可避免会使得波动理论数值计算与基于相位屏的仿真结果出现误差。当传输距离为40 m，外尺度为5 m 时，质心漂移理论计算结果与相位屏仿真的误差是0.003 9 cm，光束扩展的误差是0.001 1 cm，闪烁指数的误差是0.012 2，因此需要增加仿真次数尽可能地减小仿真误差，提升相位屏仿真的准确性。

另外，通过图7～9 还可看出，外尺度不同时，随着传输距离的增加，光束漂移、光束扩展和闪烁指数均增加；传输距离相同时，外尺度越大，光束漂移、光束扩展和闪烁指数均越大，但是相比于外尺度对闪烁指数的影响，外尺度对光束扩展和光束漂移的影响更加显著；同时当外尺度无限大时，光束漂移、光束扩展和闪烁指数均存在最大上限。

2.3 信号时域特性仿真分析

通过蒙特卡洛仿真统计到达的时间和权重进行时域特性的仿真，发射端的所有光子在同一时刻进行传输，相当于光源脉冲的时域函数是冲激函数，由于湍流效应的影响，每个光子经过传输路径上的相位屏之后，经过不同的传输距离，所需要的时间不同。在吸收系数α为0，散射系数β为0 时，海洋湍流参量动能耗散率ε=10-6，温度方差耗散率εT=10-6，湍流内尺度η=10-3，温度诱导与盐度诱导的比值ω=−2，仿真的光子数为106，在不同的海洋湍流外尺度1 m、2 m 以及无穷大时，仿真得到湍流信道传输距离为20 m、30 m、40 m、50 m 的时域仿真如图11～13。

图11 无穷大外尺度湍流时域仿真Fig.11 Time-domain simulation of infinite outer scale turbulence

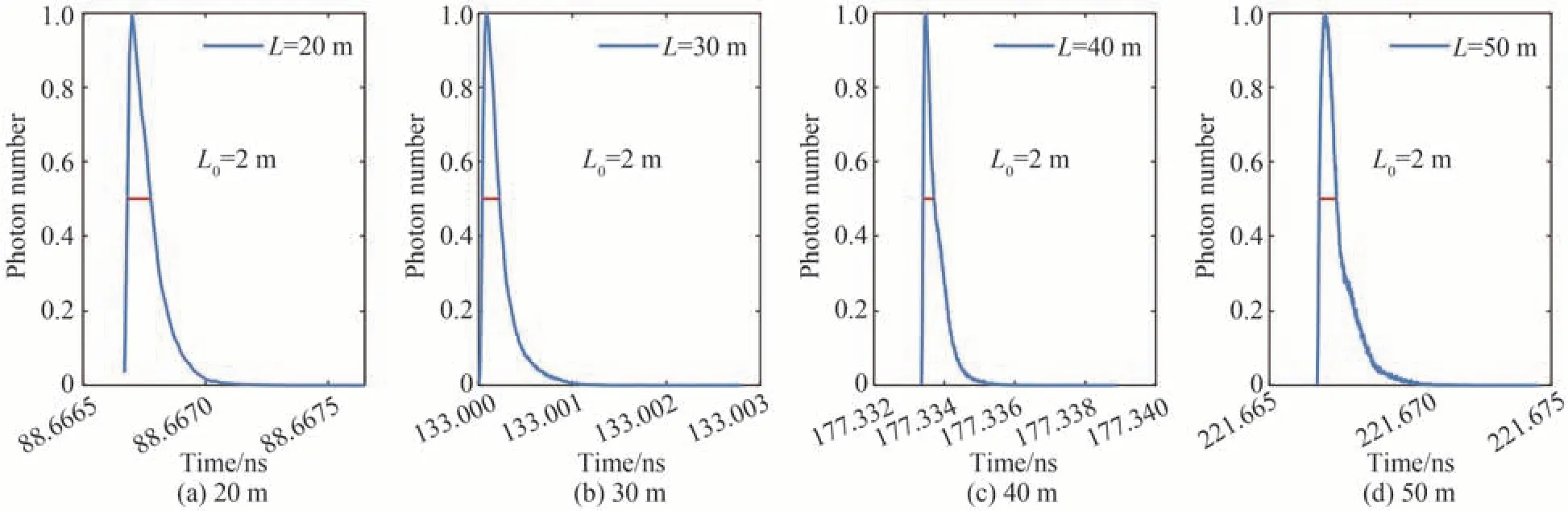
图12 2 m 外尺度湍流时域仿真Fig.12 Time domain simulation diagram of 2 m outer scale turbulence

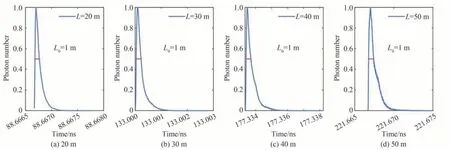
图13 1 m 外尺度湍流时域仿真Fig.13 Time domain simulation diagram of 1 m outer scale turbulence

经过海水信道统计每个光子到达接收端的时间以及同一时间到达的光子数，光子经过不同的传输距离，所需要的时间不同，体现在图11～13 中的横坐标中。为了统计时间展宽，对接收的光子数（权重）进行归一化，纵坐标为归一化的光子数即幅值，半高全宽为时间展宽的宽度。

统计时域与传输距离曲线在半高宽处对应的时间宽度，即脉冲时间展宽，结果如表1。

表1 时域展宽与传输距离关系Table 1 Relationship between time domain broadening and transmission distance

通过拟合高斯光束随传输距离变化对应的时间展宽值，得出了不同外尺度下时间展宽随传输距离的变化曲线如图14。

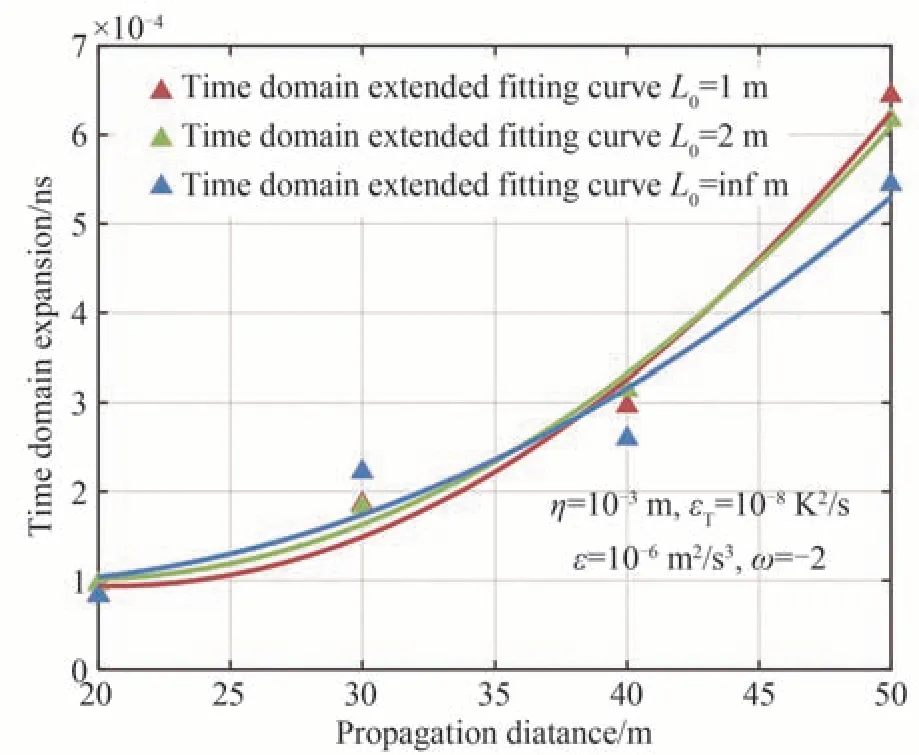
图14 湍流时间展宽拟合曲线Fig.14 Fitting curve of turbulence time domain expansion

不同外尺度下拟合的传输距离与湍流时间展宽的函数表达式如表2。

表2 外尺度与时域扩展函数关系表Table 2 Relationship between outer scale and time domain spread function

不同湍流外尺度下，受湍流影响的时域扩展值随距离的增加呈现二次函数关系。这主要是因为随着传输距离的增加，从发射端到接收端光子经过相位屏的次数增大，湍流影响增强。相比于现有的水下无线光通信能够实现的较高速率是5 Gbps［23］，该速率下的脉冲宽度小于1 ns，湍流外尺度大小对时域展宽特性的影响小于μs 量级，因此湍流外尺度大小对时域展宽特性的影响较小。在相同的湍流参数下，通过拟合的传输距离与湍流时域展宽的函数关系式可以看出时域展宽主要由传输距离决定。

3 结论

本文对所提出的指数型Nikishov 谱的修正谱模型进行了验证，并基于该模型建立了复合海水信道相位屏的蒙特卡洛仿真模型。通过对比数值计算与相位屏仿真结果，研究了信号特性随传输距离及湍流外尺度的变化，验证了相位屏方法仿真外尺度对光学特性影响的正确性，并分析了海洋湍流外尺度对信号光学特性的影响，同时研究了湍流对信号时域展宽特性的影响。结果表明：光强的概率密度分布和时域展宽特性受湍流外尺度影响较小，主要是受传输距离影响。另外，光束漂移、光束扩展和闪烁指数均小于外尺度无穷大时的光束漂移、光束扩展和闪烁指数上限。研究结果将有助于深入了解海洋湍流，并为进一步研究海水中高斯光束的传播应用提供理论依据。