基于Groebner基方法的射影不变曲线的构造
2023-06-15付泽豪李耀辉胡超棋
付泽豪 李耀辉 胡超棋


摘 要: 提出利用Groebner基方法对射影不变曲线的构造方程进行求解。首先构造出二次曲线的一般方程且其系数用参数表示;然后,利用拉格朗日乘子法得到满足最优拟合曲线时的条件,该问题由7个三次方程构成,其一般形式的解最多可以达到2187个。利用多项式环字典序下的Groebner基具有消元的性质将原问题转化为三角型方程组,进而求解。讨论了两组点集通过该类方法拟合出的不变曲线,并用实例分析了曲线在射影变换时具有拓扑结构和次数不变性。
关键词: 射影不变性; 拟合曲线; 拉格朗日函数; Groebner基
中图分类号:TP301.6 文献标识码:A 文章编号:1006-8228(2023)06-01-06
Construction of projective invariant curve based on Groebner basis method
Fu Zehao, Li Yaohui, Hu Chaoqi
(School of Information Technology Engineering, Tianjin University of Technology and Education, Tianjin 300222, China)
Abstract: In this paper, the Groebner basis method is proposed to solve the construction equations of projective invariant curves. First, the general equation of conic is constructed and its coefficients are expressed by parameters. Then, using the Lagrange multiplier method, the conditions for satisfying the optimal fitting curve are obtained. The problem consists of seven cubic equations, and the general form of the solution can reach 2187 at most. The original problem is transformed into a trigonometric system of equations by using the elimination property of Groebner basis under the dictionary order of polynomial rings. The invariant curves fitted by two point sets using this method are discussed, and the topological structure and degree invariance of curves in projective transformation are analyzed with examples.
Key words: projective invariance; fitting curve; Lagrange function; Groebner basis
0 引言
计算机视觉中,边界曲线拟合是一个经典的问题,它在人脸识别,物体形状匹配等领域都有重要的应用[1-4]。常用的边界曲线的拟合方法有:直接最小二乘法、最小平方中值法和卡尔曼滤波拟合法[5-7]。但是在模式识别中,拟合的曲线必须具有射影不变性,即射影点集的拟合曲线恰好是原始点集拟合曲线的射影,我们称这类曲线为射影不变曲线[8]。射影不变曲线能够避免摄像机视点的变化以及物体运动对目标识别产生的影响。而上述方法拟合的曲线均不具备射影不变性这一特征而不被模式识别所采用。因此,构造出射影不变曲线有其现实需要。
目前射影不变曲线的拟合方法大多采用代数距离作为拟合误差的测度,对最小代数距离进行逼近来实现拟合过程。文献[9]提出将给定变换的绝对不变量的函数作为约束,通过计算最小代数距离下的参数得到拟合曲线。该方法虽然可以获得符合要求的曲线,但是有些变换下不存在绝对不变量,方法不具备普适性。文献[10]给出了用相对不变量作为约束条件的定理,同样可以通过计算最小代数距离下的参数得到拟合曲线。该方法解决了拟合曲线普适性问题,但在后续参数的计算问题上,无法避免高次非线性方程组的求解,计算量较为庞大。
本文将曲线的系数矩阵作为约束条件,在给定变换群下,对系数矢量规格化,将曲线拟合问题转化为最优化问题,并且利用多项式环字典序下Groebner基具有的消元性质,将问题转化成三角型方程组进行求解,计算出拟合曲线的参数,最终对实验结果拟合曲线的射影不变性进行验证与分析。
1 Groebner基方法
当给出一系列点拟合边界曲线时,一方面期望保留原图形或图像的主要特征,另一方面期望曲线的计算简单且能够良好的逼近。因此,拟合时采用二次曲线进行拟合。我们主要研究当给定一组点集时,满足上述要求的曲线有多少条且它们满足什么样的性质。该问题最终转化为非线性方程組的求解问题。为了解决该问题采用Groebner基方法实现。
Groebner基理论属于计算代数几何理论。该理论于1964年由Hirona-ka H首先引入并称其为标准基。1965年Buchberger首次提出多项式理想的Groebner基算法,在随后的几十年里,不断地改进优化,其理论在研究过程中一般将问题转化为非线性多项式问题,然后利用Groebner基理论对所转化的数学问题进行求解。下面给出Groebner基的定义:
定义1 在多项式环[k[x1,…,xn]],一个有限子集[G={g1,…,gn}]的理想[I?k[x1,…,xn]],若[LT(g1),…,LT(gt)]
[=LT(I)],则[G]是一个Groebner基,其中[LTg1]表示按照某种排序(多为字典序)的多项式[g1]的首项。[LTg1,…,LTgt]表示以[LTg1,…,LTgt]为元素所生成的理想,[LTI]表示[I]中所有元素的首项组成的集合。
直观来说,Groebner基是理想的代表元素,若计算出理想的一组Groebner基,那么理想的一些好的性质可以更为方便的研究。
多项式理想保持了系统零点的不变性,即:最后得到多项式系统的解就是原多项式系统的解。具体来说,假设有一个多项式方程组:
[a11xp111+a12xp122+…+a1nxp1nn=0a21xp211+a22xp222+…+a2nxp2nn=0……an1xpn11+an2xpn22+…+annxpnnn=0] ⑴
通过利用Groebner基可以对部分元素进行消元处理,可以将原多项式系统转化为:
[a'11xp'111+a'12xp'122+…+a'1nxp'1nn=0a'21xp'211+…+a'2n-1xp'2n-1n-1=0 ……… a'n1xp'n11+m=0 ] ⑵
通過计算式⑴的Groebner基,并能保证这两个方程组的解相同,且称式⑵为三角型方程组。在对于复杂的多元多项式方程的求解过程中,可以先确定字典序,然后求得其多项式理想的Groebner基,最后计算Groebner基中多项式的根,即为原本多元多项式方程的解。
在构造平面二次曲线的过程中,需要建立拉格朗日方程求解曲线的多个参数值,即要解决高次多变元方程组的求解。这类问题在参数以及约束过多的情况下难以计算。引入Groenber基方法,其理论在研究过程中将问题转化为非线性多项式问题,利用Groebner基理论消元的性质求解拟合方程的系数,该方法不需要迭代,直接可以求出非线性方程组的解。
2 射影不变性曲线的构造
对于边界曲线的拟合,首先给定平面上的点集S,它是由[xi,yi1iN]的集合,然后利用点集的数据拟合出可以代表点集的闭合曲线,并且保证其具有射影不变性。良好的拟合曲线,需要满足两个性质:①曲线良好逼近,数据小的变化只会导致拟合曲线小的变化;②射影不变性,即射影点集的拟合曲线恰好是原始点集拟合曲线的射影。
2.1 二次不变曲线拟合理论
设所要求的二次曲线为:
[Q2x,y=Ax2+Bxy+Cy2+Dx+Ey+F=0] ⑶
该曲线也可以表示为矩阵及矢量相乘的形式,即[Q2x,y=v'Pv],其中[v]表示变元向量,[v]是[v]的转置且[v=[x,y,1]];[P]是系数矩阵,为:
[P=AB2D2B2CE2D2E2F] ⑷
为了拟合曲线,将任一点[xi,yi]到曲线[Q2x,y]的距离定义为[Q22xi,yi],点集到该曲线的距离为[1Ni=1NQ22xi,yi]。若要拟合出性质良好的二次曲线需要保证射影不变性及其对原曲线的良好逼近两点性质。为了满足第二个性质需要使点集到给定曲线的距离尽可能小;虽然[Q2x,y]与k[Q2x,y]表示同一条曲线,但是曲线外一点[xi,yi]到曲线的代数距离会随着k值的不同而不同。为了保证点集上任一点到曲线代数距离的惟一性,构造不变射影曲线时增加约束条件即要求拟合时二次曲线系数矩阵的行列式[|P|=1]。最终,将二次曲线的不变性拟合转化为带有约束条件的优化问题,若给定点集S,就可以得到:
[mini=1NQ22xi,yis.t. P=1] ⑸
利用拉格朗日乘子法,将带有约束条件的优化问题进一步转为无约束条件的优化问题:
[L=i=1NQ22xi,yi+λ(P-1)] ⑹
其中,[λ]为拉格朗日乘子,可得到一个七元三次非线性方程组:
[?L?A=2i=1Nx2i*Q2xi,yi+λCF-E24=0?L?B=2i=1Nxiyi*Q2xi,yi+λDE4-BF2=0?L?C=2i=1Ny2i*Q2xi,yi+λAF-D24=0?L?D=2i=1Nxi*Q2xi,yi+λBE4-CD2=0?L?E=2i=1Nyi*Q2xi,yi+λBD4-AE2=0?L?F=2i=1NQ2xi,yi+λAC-B22=0P=ACF+BDE4-CD24-AE24-B2F4-1=0] ⑺
由于上述方程组是非线性的,直接消元非常困难,采用数值法求解不能保证得到满足上述方程的所有解,根据前述的Groebner基理论得知其具有消元的性质,若计算非线性方程组生成理想在变元字典序下的Groebner基会得到另一个非线性方程组且是一个三角型方程组,这样我们就容易求出其中的单变元方程的解,然后将该变元的解代入含有两个变元的方程求出另一个变元的解,最后,计算出所有变元的解。具体计算时,首先将式⑺中的变元按字典序排序为[{λ,A,B,C,D,E,F}],再将式⑺中方程组左侧的各项构建系统的理想,然后计算该理想的Groebner基,可得到如下一般形式的方程组:
[k=0Na1kFk=0k=0Na2kFk+b2E=0k=0Na3kFk+b3D=0k=0Na4kFk+b4C=0k=0Na5kFk+b5B=0k=0Na6kFk+b6A=0k=0Na7kFk+b7λ=0] ⑻
该方程组第一个方程只含有变元F,因此求解过程只需要先求出F,再将F的值代入第二个方程求解出E的解,这样逐一得到其他所有变元的值。实际上,有时在计算Groebner基时并非得到的方程数和变元一样多,后面具体实例中可以看到,有时我们得到的方程组中方程的个数并不是七个而是八个,但是变元个数仍然只有七个。这种情况,必有一个方程和其他方程的变元个数一样多,计算时,取这两个方程的任一个计算新增加变元的解,用另外一个方程进行验证,去掉不满足这两个方程的解。这样,可以排除非拟合曲线的解,在计算后面其他变元的解时可以大大降低非线性方程组的求解复杂度。这是一种特殊的形式,相比一般形式可以节约一定的算力。
根据代数方程组的一般定理可知七元三次方程组在复数域上最多可以有2187个解,其中很多解可能是复数解并且对于实际拟合曲线无意义,因此,讨论一般情况下的射影曲线的形式与参数之间的关系也会非常复杂。在实际的边界拟合问题上,并非要计算出方程组的全部解,我们只需要在全部实数解中得到与点集距离最近的那一条曲线。而且在求解变元的过程中,变元[λ]也并非是曲线所需要的参数,因此可以不作计算,来达到减轻工作量的目的,下面通过实例来讨论点集曲线拟合所得到的解。
2.2 不变曲线拟合的实例讨论
为了计算具体的不变拟合曲线,假设目标边界过点[q1:5,0,q2:0,5,q3:-5,0,][q4:0,-5,q5:3,4,q6:-3,-3]。采用前述计算二次曲线的理论拟合该目标边界曲线,使其满足射影不变性。
将点集坐标代入式⑺可以得到如下非线性方程组:
[2824A+ 378B + 450C + 18E+ 136F+λCF -E24=0378A + 450B+546C+18D+42E+42F + λDE4-BF2=0450A+545B+3174C+42D+74E+150F + λAF-D24=018B+42C+136D+42E+λBE4-CD2=018A+42B+74C+42D+150E+2F+λBD4-AE2=0136A+42B+150C+2 E+12F+λAC-B22=0ACF+BDE4-CD24-AE24-B2F4-1=0] ⑼
将式⑼方程组左侧的各多项式作为集合,构造多项式理想,确定变元的字典序为[[λ, A, B, C, D, E, F]],计算该序下的Groebner基。为了构造二次曲线,当选定6个点构成点集,通过计算Groebner基,恰能生成七个变元的三角型方程组。我们先得到多项式系统生成理想,然后计算该理想在字典序[{λ,A,B,C,D,E,F}]下的Groebner基,得到消元理想,其中含有七个多项式,其形式如下:
[G1=f1FG2=f2E,FG3=f3D,FG4=f4C,FG5=f5B,FG6=f6A,FG7=f7λ,F] ⑽
由式⑽可以看出新得到的多項式系统自上至下每个多项式新增一个变元,令系统等于0得到三角型方程组,其中第一个多项式[G1]只含有单变元F且各项的次数如下:
[G1=a69F69+a66F66+…+a3F3+a0=0] ⑾
其中,[a0,a3,…,a69]是各此项的系数且均为常数,因其为单变元方程故易得到F的解。根据代数基本定理,其最多有69个解(重根以重数计)。在这69个解中只有五个实数解。再将F的实数解分别代入[G2,G3,G4,G5,G6],在这些多项式中同样包含了关于F的高次项以及其他单一变元的单次项,因此,每一个F的解都可以对应其他变元的惟一解,由于其他方程过于冗长不再一一列举。最终,可以得到5组实数解。而[G7]中的变元[λ]由于不属于曲线的参数,因此不作计算。5组实数解结果如表1所示。
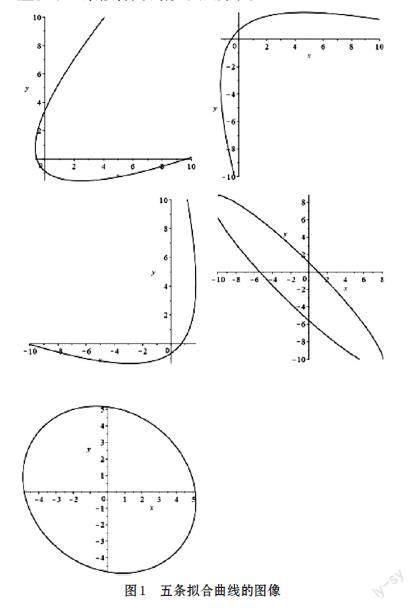
将上述参数代入⑶式中,得到五个方程,分别对应以下五条拟合曲线,如图1所示。
这五条曲线包含了两条椭圆,三条抛物线。说明通过点集拟合出的曲线具有不惟一性。并且根据二次不变曲线拟合理论,这五条拟合曲线均满足射影不变性的条件。不过,并非所有不变曲线都可以做到良好逼近,上述例子中所给出的点集分布可以看出,该点集更加适合通过椭圆来拟合曲线,通过比较点集到曲线的代数距离[1Ni=1NQ22xi,yi]可以验证出这一点,得到4条曲线中最佳逼近的那一条拟合曲线。4条拟合曲线到[q1, q2,q3,q4,q5,q6]的距离如表2所示。
根据结果可以明显比较出曲线5具有更加良好的逼近条件,因此拟合该点集的最佳曲线方程应当为:[-0.347x2+0.105xy-0.343y2+0.089x+0.101y+8.586=0]。
上例中得到的Groebner基只是一般情况,并非所有拟合点集过程都可以得到规整的三角型方程,不过其方程仍然可以转化为非线性方程组来计算。下面将点集中[q6:-3,-3]改为[q7:-3,-4],进行计算,可以发现这一现象。
将点[q1,q2,q3,q4,q5,q7]的坐标代入式⑺可以得到如下非线性方程组:
[2824A+ 432B + 576C + 136F+λCF -E24=0432A + 576B+768C+48F + λDE4-BF2=0576A+768B+3524C+164F + λAF-D24=0136D+48E+λBE4-CD2=048D+164E+λBD4-AE2=0136A+48B+164C+12F+λAC-B22=0ACF+BDE4-CD24-AE24-B2F4-1=0] ⑿
将式⑿方程组左侧的各多项式作为集合,按照相同字典序排列后求出Groebner基含有八个多项式,其具体形式如下:
[G1=f1FG2=f2E,FG3=f3E,FG4=f4D,E,FG5=f5C,FG6=f6B,FG7=f7A,FG8=f8λ,F] ⒀
其中,[G2]和[G3]都是包含了變元E和F的多项式,且[G4]含有三个参数,但这仍然是非线性方程组,可以先舍弃[G2]的方程组,计算得到69组解,其中11组为实数解。再将这11组解带入方程[G2=0]进行验证,可以发现均满足等式,因此这11组解就是式⑿的实数解,具体结果如表3所示。
通过比较曲线与点集的代数距离可以发现,点集的所有点均落在拟合曲线[-0.342x2-0.343y2+8.550=0]上,且曲线符合射影不变性特征。
上文两例可以说明该方法对于拟合不变曲线具有普适性,通过Groebner基理论转化的非线性方程组都可以更加简单得求出原本方程组的解,得到的最优解即为最佳拟合曲线的参数。
2.3 曲线射影不变性分析
上节所求得曲线应当保持射影不变性的特征,即射影点集的拟合曲线恰好是原始点集拟合曲线的射影。假设点集[(xi,yi)(1iN)]的拟合曲线为[Q2x,y=Ax2+Bxy+Cy2+Dx+Ey+F=0],在经过射影矩阵[τ=a11a12a13a21a22a23a31a32a33]的射影变换后,点集中的点坐标改变得:
[x'i=a11xi+a12yi+a13a31xi+a32yi+a33y'i=a21xi+a22yi+a23a31xi+a32yi+a33] ⒁
点集[(x'i,y'i)(1iN)]即为射影变换后的点集,曲线[Q2x,y]经过τ的射影变换后,得:
[Q'2x,y=A'(x')2+B'x'y'+C'(y')2+D'x'+C'y'+F'=0] ⒂
其中[x'=a11x+a12y+a13a31x+a32y+a33y'=a21x+a22y+a23a31x+a32y+a33],可以解出式⒂的参数[A',B',C',D',E',F'],若式⒂可以拟合出点集[(x'i,y'i)(1iN)],则说明拟合曲线[Q2x,y]具有射影不变性的特征,反之则没有。
根据此判据,可以通过一次射影变换对上节中两条曲线的射影不变性进行如下验证。
设边界点[q1,q2,q3,q4,q5,q6],[q7]经过变换矩阵τ后变为[q'1,q'2,q'3,q'4,q'5,q'6],[q'7],射影变换矩阵τ为:
[τ=122212001]
则边界点的坐标变换根据⒁式可得:
射影变换后的拟合曲线如图2所示。
可以看出,射影变换后的曲线可以很好的拟合出影射变换后的点集,其拓扑结构仍是椭圆,其方程仍是二次方程,故曲线[-0.347x2+0.105xy-0.343y2+0.089x+0.101y+8.586=0]和[-0.342x2-0.343y2+8.550=0]拟合边界点,不仅满足曲线的良好逼近,而且具有射影不变曲线的性质。证明了本文方法可以高效、准确地进行曲线拟合。
3 总结
本文构造出平面曲线的二次曲线射影不变性拟合一般方法。该方法将拟合过程中的一般非线性方程通过计算变元字典序的Groebner基消元得到三角型方程组,然后进行求解。该方法克服了Gauss-Seidel迭代只能求解线性方程组,而Newton迭代只能求解单变元非线性方程组的问题。在计算机视觉领域,对运动与模糊物体的识别的底层算法进行了优化。将来随着算力的提升,可以利用该方法对四次曲线的拟合对这类曲线进行更精确的拟合。
参考文献(References):
[1] Yang F, Tan X. Establishment and Analysis of Face
Recognition Model Based on Least Square Method[C]// 2018 International Conference on Mathematics, Modelling, Simulation and Algorithms (MMSA 2018),2018:67-70
[2] Wu W, Qian C, Yang S, et al. Look at Boundary: A
Boundary-Aware Face Alignment Algorithm[C]// 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition.IEEE,2018:2129-2138
[3] MerkerL, Will C, Steigenberger J, et al. Object Shape
Recognition and Reconstruction Using Pivoted Tactile Sensors[J]. Mathematical Problems in Engineering,2018(1):1-11
[4] Fan Y N, Lang B. An Object Shape-matching Method
Using Contour Orientation Feature[J].Computer Technology and Development,2018,28(1):88-92
[5] Fitzgibbon A, Pilu M, Fisher R B. Direct least square fitting
of ellipses[J]. IEEE Trans.patt.anal.mach.intell,1999,21(5):476-480
[6] Roth G, M.D. Levine. Extracting Geometric Primitives[J].
Academic Press, Inc,1993,58(1):1-22
[7] PorrillJ. Fitting ellipses and predicting confidence
envelopes using a bias corrected Kalman filter[J]. Image & Vision Computing,1990,8(1):37-41
[8] 孙即祥.模式识别中的特征提取与计算机视觉不变量[M].
北京:国防工业出版社,2001
[9] Reiss Thomas H. Recognizing Planar Objects Using
Invariant Image Features[M]. Springer-Verlag,1993
[10] Forsyth D, Mundy J L, Zisserman A, et al. Projectively
invariant representations using implicit algebraic curves[J]. Image and Vision Computing,1991,9(2):130-136
[12] 徐正伟,吴成柯.二维形状的透视不变性识别[J].自动化
学报,1995,21(4):431-438
[11] Rajashekhar, Chaudhuri S, Namboodiri V P. Image
retrieval based on projective invariance[C]. Image Processing, 2004. ICIP '04. 2004 International Conference on. IEEE,2004:405-408
[13] DavidCox, JohnLittle, DonalO'shea. Ideals, varieties, and
algorithms:anintroductional algebraic geometry and commutative algebra[M]. 世界图书出版公司北京公司,2013
[14] 齐紫微.应用Groebner基方法求解代数方程组的解[J].
装甲兵工程学院学报,2007,21(4):90-91
[15] 张政武.空间二次曲线代数不变量的几何解释[J].机械
科学与技术,2008,27(12):1670-1672
[16] 袁立行,郑南宁.一种新的空间透视不变量计算方法[J].
西安交通大学学报,1997,31(1):84-89
[17] 赵临龙.二阶线性微分方程不变量解法的新类型[J].西南
民族大学学报(自然科学版),2018,44(4):402-405
[18] 张文哲.参数Groebner系统在偏微分代数方程中的应用[J].
数学的实践与认识,2021,51(24):171-180
[19] Baik, Hyungryul, Samperton, et al. Spaces of invariant
circular orders of groups[J]. Groups Geometry & Dynamics,2018,12(2):721-763
[20] 嚴飞,张铭伦,张立强.基于边界值不变量的对抗样本检测
方法[J].网络与信息安全学报,2020,6(1):38-45
