挖掘问题本质　巧用模型求解

2023-06-14康敏

初中生世界·九年级 2023年5期

康敏

解决平行四边形综合类问题，我们要学会结合图形抓住已知条件中的关键信息，寻求已知条件的内涵，结合所求的结论，从前向后分析，再从后向前逆推，挖掘问题的本质，找准解决问题的关键点，最终探究到适当的数学模型来解决问题。

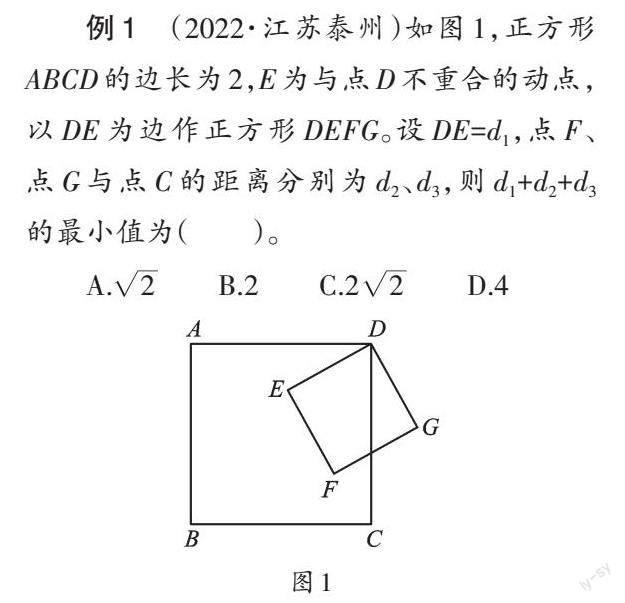
例1 （2022·江苏泰州）如图1，正方形ABCD的边长为2，E为与点D不重合的动点，以DE为边作正方形DEFG。设DE=d1，点F、点G与点C的距离分别为d2、d3，则d1+d2+d3的最小值为（）。

A.[2]B.2C.[22]D.4

【分析】如图2，连接CF、CG，求d1+d2+d3的最小值，就是求DE+FC+GC的最小值。但是DE与另两边没有公共点，这就需要把“折线段”的和转化为“直线段”的和，所以要转化线段DE。由四边形DEFG是正方形，可得DE=EF。结合图形，还需要把CG也转换，这里就是难点和关键点。由四边形ABCD是正方形，得到∠ADC=∠EDG=90°，AD=CD，能推出∠ADE=∠CDG，这样就联想构造三角形全等。连接AE，利用“SAS”证明出△ADE≌△CDG，得出AE=CG，把DE+FC+GC转化为EF+FC+AE。所以，当A、E、F、C四点共线时，即得最小值。

解：如图2，连接CF、CG和AE。

∵四边形ABCD是正方形，四边形DEFG是正方形，

∴AD=CD，∠ADC=∠EDG=90°，DE=EF=DG。

∴∠ADE=∠CDG。

在△ADE和△CDG中，

[AD=CD，∠ADE=∠CDG，DE=DG，]

∴△ADE≌△CDG（SAS）。

∴AE=CG。∴DE+CF+CG=EF+CF+AE。

当A、E、F、C四点共线时，能取到最小值，即AC的长。

∵AC=[AD2+CD2]=[22+22]=[22]，

∴d1+d2+d3的最小值为[22]。

故选C。

【点评】本题主要考查正方形的性质、全等三角形的证明、勾股定理的运用、转换思想等。正确构造全等三角形求出边相等是解决本题的难点，此题的全等证明是“手拉手模型”。求顺次相连的多条线段和最小，关键是把“折线段”的和转化为“直线段”的和，简称“化折为直”。当这几点共线时，线段和最小，本质上运用了两点之间线段最短，体现了由一般到特殊的数学思想。

例2 （2022·江苏连云港）如图3，四边形ABCD为平行四边形，延长AD到点E，使DE=AD，且BE⊥DC。

（1）求证：四边形DBCE为菱形；

（2）若△DBC是边长为2的等边三角形，点P、M、N分别在线段BE、BC、CE上运动，求PM+PN的最小值。

【分析】（1）如图3，先根据平行四边形的性质，得AD=BC和AD∥BC。已知DE=AD，得到BC和DE的数量关系和位置关系，从而证明四边形DBCE为平行四边形，再根据BE⊥DC，即可证得四边形DBCE为菱形。

（2）如图4，点P、M、N都是动点，所以PM+PN是变化的，是“折线段”的和。因此，求其最小值时，要先变“折线段”为“直线段”，即利用转换思想，找不变量。作点N关于BE的对称点N'，点N'在DE上，根据菱形对称性得到PM+PN=PM+PN'，PM+PN的最小值即为菱形的高。构造直角三角形，利用三角函數即可求得高的值。

（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC。

∵DE=AD，∴DE=BC。

∵点E在AD的延长线上，∴DE∥BC。

∴四边形DBCE为平行四边形。

又∵BE⊥DC，∴四边形DBCE为菱形。

（2）解：如图4，由菱形对称性得点N关于BE的对称点N'在DE上，

∴PM+PN=PM+PN'。

当P、M、N'共线时，PM+PN=PM+PN'=MN'。

过点D作DH⊥BC，垂足为H。

∵DE∥BC，∴MN'的最小值即为平行线间的距离DH的长。

∵△DBC是边长为2的等边三角形，

∴在Rt△DBH中，∠DBC=60°，DB=2。