小小“点”,大作用
2023-06-14游淑溶
游淑溶

尺规作图是初中阶段重要的几何作图方法。面对平行四边形作图题,当你手中只有一把无刻度的直尺时,你是否感到手足无措呢?不要急,这时候我们可以借助平行四边形的对称中心这个小小“点”,让它来发挥大作用。
一、小小“点”牵手角平分线
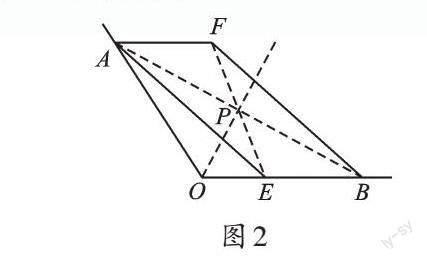
例1 如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,在图中画出∠AOB的平分线。(只用无刻度的直尺作图,请保留画图痕迹,不写作法。)
【分析】我们平时用圆规和直尺很容易作出已知角的平分线,但这道题要求用无刻度的直尺作角的平分线,也就是说只能借助直尺連线,该如何画呢?从题目中的已知条件OA=OB,我们发现,两条有一公共端点的线段(不在同一直线上)长度相等,说明存在等腰三角形,其实就是作等腰三角形顶角∠AOB的平分线。因为没有圆规和量角器,所以不能直接作角平分线,只能从其他方面出发。我们知道等腰三角形的顶角的角平分线、底边上的中线及底边上的高线是互相重合的,那么我们就可以从底边AB出发。而四边形AEBF是平行四边形,我们不难看出AB是[?]AEBF的一条对角线,也就知道了AB的“双重”身份,即AB既是等腰三角形的底边,又是平行四边形的对角线。这样我们就很容易想到平行四边形的对称中心这个特殊的点了。我们把它看成等腰三角形的底边AB上的中点,再用无刻度的直尺连接点O和小小“点”即可。
解:如图2,连接AB、EF,交于点P,射线OP即为所求。
二、小小“点”圆梦相等线段
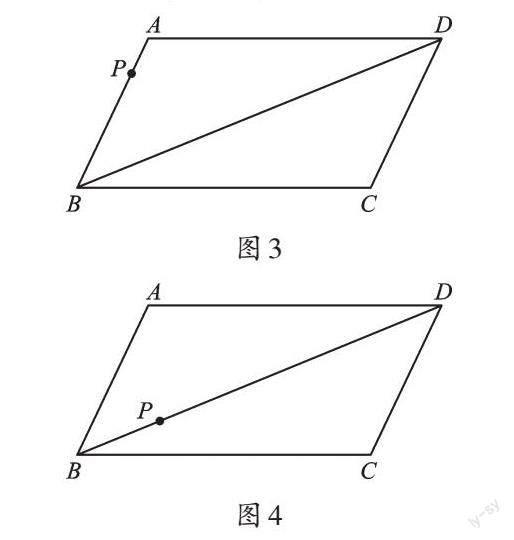
例2 已知BD为[?]ABCD的对角线,请仅用无刻度的直尺分别按下列要求画图。(保留画图痕迹。)
(1)如图3,点P为AB上任意一点,在CD上找一点Q,使CQ=AP。
(2)如图4,点P为BD上任意一点,在BD上找一点Q,使DQ=BP。
【分析】(1)我们知道平行四边形是中心对称图形,点A与点C、点B与点D关于小小“点”(对称中心)对称,线段AB与CD也关于它中心对称。明白了这一点,我们不难发现,这题就是找点P关于小小“点”的中心对称点。(2)在平行四边形的对角线上如何作相等的线段?其实我们可以借助第(1)问的方法,由于点P在对角线上,点A、点P所在直线与边BC有交点(设为点M),所以我们找出点M关于小小“点”O的对称点N,线段CN与BD的交点就是我们要找的点。
解:(1)如图5,点Q为所作。
(2)如图6,点Q为所作。
在解决与平行四边形有关的作图题时,我们可以尝试从平行四边形的对称中心入手,发挥这个小小“点”的作用,轻松解决平行四边形中用无刻度的直尺作图的问题。
(作者单位:江苏省泰州市姜堰区城西实验学校)
