基于深度强化学习的分布式UUV集群任务分配算法*

郝冠捷,姚 尧,常 鹏,张晓霜

(江苏自动化研究所,江苏 连云港 222061)

无人水下航行器(Unmanned Underwater Vehicles, UUV)是执行水下任务的主要工具之一。单个UUV的性能有限,复杂的大范围任务需要通过UUV集群来解决,目前UUV集群的组织架构主要分为集中式[1]和分布式[2]。集中式对通信带宽、速率和可靠性有较高的要求,由于水下环境复杂,集中式难以获得全局信息进行任务分配。分布式不依赖“指挥中心”,每个UUV都是拥有自主决策能力的个体,在执行任务的过程中可靠性、鲁棒性更高,对通信能力的要求较低,更加适合在环境复杂多变的海洋中解决任务分配问题。

本文研究分布式UUV集群及其任务分配问题,该问题是属于多智能体任务分配的一类NP完全问题[3],随着任务和UUV数量的增加寻求可行解的时间呈指数级增长,同时分布式架构下的多智能体任务分配需要解决信息一致性问题。目前无人平台下的分布式任务分配算法研究主要有基于市场机制的拍卖算法和合同网算法[4],该类算法存在时延问题且较为依赖稳定的通信环境,无法处理任务空间存在动态不确定性的规划问题;基于分布式马尔科夫决策过程的适值迭代法和联合策略迭代法[5]等算法可以解决动态环境下的在线任务分配问题,但是普遍适用性较差;基于博弈论思想的分布式任务分配策略提出时间不长,仍处于研究阶段。集中式算法主要分为优化算法和启发式算法[6]两类,受限于集中式框架,对通信环境要求较高且动态性能响应慢,不适用于水下无人平台。

本文考虑UUV的水下通信和探测能力限制问题,针对分布式UUV集群的任务分配问题,研究深度强化学习及其在任务分配问题中的应用,提出了一种基于深度强化学习的分布式UUV集群任务分配算法[7-8]。深度强化学习具备强大的函数逼近能力和自主学习能力,适用于解决具有高维状态动作空间的多智能体任务分配问题,近几年已有学者将深度强化学习应用在最优控制、组合优化问题和调度问题中,对该类问题在求解时间和性能优化方面取得了显著的提升。

1 环境模型

1.1 问题描述

假设一片水域有一队由若干个同构的UUV组成的集群,UUV集群覆盖整个水域,若干个任务随机出现在这片水域内。假设任务之间不存在相互依赖关系,即每个任务可以独立于其他任务执行。本文的目标是在单个UUV仅能获得周围局部信息的情况下,解决面向多任务的UUV集群任务分配问题。

给定UUV集群集合

R={r1,r2,r3,…,rm}

(1)

给定任务集合

T={t1,t2,t3,…,tn}

(2)

给定任务n的价值表示为

V={v1,v2,v3,…,vn}

(3)

对于UUV个体ri,存在一个任务执行队列:

Qi={qi1,qi2,qi3,…,qis}

(4)

上述公式中UUV个体为ri,i=1,…,m,任务为tj,j=1,…,n,vj表示任务tj的价值。设定UUV集群是同构的,对于所有UUV个体ri,给定通信距离为xc,给定探测范围为xd。对于UUV个体ri, 集合Ri={ra,rb,rc,…,rs}表示在ri通信范围内的UUV,即与其距离小于xc的其他UUV,其中Ri∈R;集合Ti={ta,tb,tc,…,ts}表示ri探测到的任务,即与其距离小于xd的任务,其中Tj∈T。

所有任务执行队列Qi中的元素都不相同,即qip≠qiq。所有属于队列Qi的元素都属于T,并且不同任务执行队列中的元素也不同,即Qi∩Qj=∅,其中Qj表示UUV个体rj的任务执行队列。所有UUV个体的任务执行队列集合为Q,即满足公式:

Q={Q1,Q2,Q3,…,Qm}=T

(5)

1.2 分布式UUV集群任务分配数学模型

1.2.1 效用公式

UUV集群任务分配问题是一类优化问题,决定一个任务是否分配给一个UUV的决定性因子被称为效用,效用可以由单一变量描述也可以由多个变量组成,例如任务执行距离、电池电量、任务优先级等,UUV执行一个任务的效用越大,那么这个任务越有可能分配给它。假设UUV和任务之间相互独立,每一个UUV都能够对探测范围内的所有任务估计效用,给定UUV个体ri执行任务tj可以获得效用Uij,考虑UUV主要用于探测、侦察、跟踪等任务,本文使用的效用由UUV执行任务的距离和UUV的剩余能源组成,本文提出效用Uij的计算公式如下:

(6)

(7)

(8)

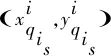
1.2.2 任务分配目标函数

本文提出算法的优化目标有3个,对于每一个UUV个体,在自身探测范围内,第一个目标是实现UUV集群完成任务时间尽可能短,即使效用最小的UUV其效用尽可能大;第二个是实现UUV集群总效用尽可能大。

假设对于UUV个体ri,其探测到的UUV个数为a、任务个数为b,UUV集合为Ra,任务集合为Tb,每个UUV分配后的任务队列为Qi={qi1,qi2,qi3,…,qis},i=1,2,…,a,有Q1∪Q2∪…∪Qa=Tb。

给出任务分配的两个目标函数如下:

(9)

(10)

UUV个体在局部对探测到的任务和其他UUV个体进行任务分配后,公式(9)表示计算每一个UUV自身任务队列的总效用,使总效用最低的UUV个体效用最大化,公式(10)表示使所有UUV效用的总和最小化。

2 基于深度强化学习的分布式UUV集群任务分配算法

2.1 深度强化学习

强化学习是智能体不断与周围环境交互并积累经验,从经验中学习如何尽可能好地达到自己目标的过程。智能体在环境中所处的状态、智能体的动作、智能体在不同状态下采取动作的策略以及智能体采取动作之后获得的奖励是强化学习研究的主要对象,状态-动作空间随着问题复杂性的增加而呈指数级上升,深度神经网络是一种很好的函数逼近方法。结合了两者的深度强化学习主要分为基于策略的方法(学习策略)、基于值的方法(学习值函数)和基于模型的方法(学习模型),还有一些组合方法[9]。本文提出一种改进的基于学习值函数的双重深度Q网络算法[10](Double Deep Q-Networks),简称改进DDQN算法,本文在算法的动作选择环节提出了一种基于Boltzmann策略的概率下降动作选择策略,该算法显著增加了智能体学习到更好动作的概率,使算法更快地收敛至优化目标。

2.2 奖励函数

智能体能否不断地优化目标函数,关键在于从环境中不断尝试获得的奖励,给定状态、动作和奖励的定义(本节中的r均表示奖励,其他节中表示UUV个体):

st∈S是状态,S是状态空间,

at∈A是动作,A是动作空间,

P(st+1∣st,at)是环境的状态转换函数,

rt=R(st,at,st+1) 是奖励,R是奖励函数。

UUV集群在任务分配过程中下一时刻的状态st+1只由前一时刻的状态st和动作at决定,具备马尔可夫特性,即满足下列公式

st+1～P(st+1∣st,at)

(11)

为了完成对问题的表述,需要对智能体想要最大化的目标进行参数化。本文用一个事件的轨迹来定义回报R(τ),其中τ=(s0,a0,r0),…,(sT,aT,rT)。

(12)

公式(12)将回报定义为轨迹中所有奖励的加权和,其中γ∈[0,1]是加权因子,t∈(0,T)表示事件从0时刻开始到T时刻结束,其中的每一个时刻为一个时间步。

目标J(τ)是许多轨迹上回报的期望值,如下式所示:

(13)

回报R(τ)是所有时间步t=0,…,T上的加权奖励γtrt之和。目标J(τ)是许多事件的平均回报。期望值解释了动作和环境中的随机性,也就是说在重复运行中,回报可能并不总是相同的。最大化目标和最大化回报是一样的。加权因子γ∈[0,1]是一个重要的变量,它改变了后续奖励的估值方式。γ越小,在后续的时间步中给予奖励的权重就越小,目标变得越“短视”;γ越大,在后续的时间步中给予奖励的权重就越大,目标变得越“远视”。

根据本文所描述的分布式UUV集群任务分配数学模型,奖励函数采用如下公式:

(14)

(15)

xij∈{0,1},i=1,2,…,m,j=1,2,…,n

(16)

其中,xij表示任务tj是否分配给UUV个体ri,若tj分配给ri则xij=1,否则xij=0。公式(15)表示每一个任务只能分配给一个UUV。公式(14)中,f(tmin)表示过去所有分配结果样本中的最小效用UUV个体的最大效用值样本,g(tmax)表示过去所有分配结果样本中的最短总距离样本,在进行完一个分配动作后,若此任务之前没有被分配过,则奖励为0;若此任务之前已经被分配过了,则奖励为-1;若所有任务都已分配,且该分配结果比之前最好的一次样本总任务效用更大,最小效用UUV个体的任务效用更大,则奖励为f(t)g(t)。

2.3 基于改进DDQN的多智能体任务分配算法

2.3.1 双重深度Q网络

DDQN是一种基于值的时序差分(TD)算法[11],它学习的是动作值函数Qπ(s,a)[12],并且学习的是最优Q函数,DDQN的网络更新公式如下:

am=arg maxQm(St+1,a)

(17)

Qm(st,at)=Qm(st,at)+η*[Rt+1+γQt(st+1,am)-Qm(st,at)]

(18)

其中st+1表示下一时刻的状态。这里的双重网络指的是有两个结构相同的主网络Qm和目标网络Qt,主网络Qm用来获得在下一状态st+1中具有最高Q值的动作am,而目标网络是使用am来更新网络参数,双重Q网络使得学习过程更加稳定。

2.3.2 概率下降动作选择策略

DDQN虽然是一种异策略算法[13],但是其智能体收集经验的策略仍然很重要。首先,智能体面临探索和利用的权衡问题,在训练开始时智能体应该快速地探索状态-动作空间,以增加发现在环境中进行动作策略的机会。随着训练的进展和智能体学习量的增多,应该逐渐降低探索率,花更多的时间去利用已学到的东西;其次,复杂问题的状态-动作空间往往很大,智能体不太可能到达对这个空间的所有部分都进行良好Q值预估的水平,智能体应该集中学习一个好的策略会经常访问的状态和动作,那么仍然有可能在这样的环境中获得良好的性能。Boltzmann策略[14]是一种智能体在探索状态-动作空间时选择动作的策略方式,其选择动作的概率遵循下面的公式

(19)

本文通过应用softmax函数[15]构造了一个在状态s下所有动作a的Q值概率分布;通过设置一个温度参数τ∈(0,∞),将softmax函数参数化,以此控制所得出的概率分布的均匀性和集中性。较高的τ值使得分布更加均匀,较低的τ值使得分布更加集中。本文在训练开始时使用一个较大的τ值,随着训练的进展,逐渐使τ值衰减。

本文提出一种基于Boltzmann策略的概率下降动作选择策略,对于概率pboltzmann(a|s),设置下降参数δ,每经过δ次训练,则选用第二大概率p的动作,每经过2δ次训练,则选用第三大概率p的动作,其余时刻遵循Boltzmann策略。

2.3.3 优先经验回放

DDQN算法的异策略性使得智能体不必丢弃已获得经验,设置一定大小的经验回放内存区存储智能体最近收集到的经验数k。如果内存是满的,那么最旧的经验就会被丢弃,为最新的经验腾出空间。智能体每次训练时,都会从经验回放内存区中优先抽取学习不到位的样本,这些经验样本将用来更新Q函数网络的参数,优先顺序的基准是Bellman方程[16]中价值函数的绝对误差,由以下公式表示

Δ=Rt+1+γ*maxa[Q(st+1,a)-Q(st,at)]

(20)

其中Rt+1表示下一时刻的奖励,γ为学习率系数。

2.3.4 神经网络结构

1)输入层—状态

针对分布式UUV集群的特点,本文使用UUV个体ri的任务序列与目标任务tj的分配情况作为状态输入,设有m个UUV和n个任务,即输入神经元个数为m+n。

2)隐含层

本文将对包含16个UUV个体的UUV集群进行训练,使用2层隐含层,根据每个个体局部的UUV及任务数量动态设置相应的隐含层神经元个数为m*n+2。

3)输出层—动作

本文使用目标任务点tj分配给某一UUV个体ri作为动作输出,即输出神经元个数为m*n。

如图1所示,当m=3,n=2时,输入神经元的数量为5,输出神经元的数量为6,隐含层神经元的数量为8,输出(1,0,0,0,0,0)表示任务t1分配给UUV个体r1。

图1 神经网络结构图Fig.1 Neural network structure

2.4 分布式UUV集群一致性协调SAC算法

每一个UUV个体自身都会有相应的数据结构来存储全局状态信息,UUV个体通过接收邻近个体的信息来逐步更新这个全局状态信息,UUV个体之间的信息和决策会存在冲突的情况,本文提出了一种二次分配一致性(Second Allocation Consistency, SAC)算法来解决该问题。

2.4.1 态势信息一致性

在UUV集群任务分配环境中,态势信息是指每一个UUV个体自身的位置坐标、任务序列以及任务目标点的坐标。UUV个体ri会周期性地广播发送自身位置(rix,riy)和要执行的任务序列Qi={qi1,qi2,qi3,…,qis}以及探测到的任务,来保证UUV集群对于全局信息的逐步更新一致。

2.4.2 决策信息一致性

在UUV集群任务分配环境中,决策信息是指每一个UUV个体对自身覆盖范围内的所有UUV个体分配探测到的所有任务,在整个任务分配过程中,本文提出了一种二次分配一致性(SAC)算法来解决两种需要信息一致性协调的情况,第一种是同一个任务被分配给了多个UUV,第二种是UUV个体接收到了其他UUV指派的新任务。

假设对于UUV个体ri,对探测到的其他UUV个体Ri={ra,rb,rc},任务Ti={td,te,tf}进行任务分配。如果ra的任务序列Qa与rb的任务序列Qb中的任务出现了相同的任务tf,即qaf=qbf,xaf=xbf=1,那么说明任务tf被分配给了两个UUV个体ra和rb。此时UUV个体ra和rb都对双方包含任务tf的任务序列进行二次最优任务分配,此时的目标函数如下:

(21)

ra和rb由于此时是连通状态,双方信息一致,所以各自对双方的分配结果是一致的,双方都比较maxf(a)与maxf(b)的大小,若自身执行任务tf的效用更大,则保留任务tf,若自身执行任务tf的效用更小,则从自身任务序列中删除。

UUV个体将接收到其他UUV指派的新任务添加到任务序列添加,或者与其他UUV一致协调删除任务后,都以公式(21)为目标函数重新对任务序列进行优化分配,此时是一个TSP问题。

本文提出了二次分配一致协调算法,由于UUV个体不断地广播自身信息,只要其他UUV个体接收到一次,就可以进行一致性协调,不需要等待其他UUV应答,决策速度更快,在水下通信环境受限的情况下能提升任务分配决策的可靠性和稳定性。

2.5 算法实现

完整算法流程的伪代码分为两部分,分别是基于改进DDQN的多智能体任务分配算法和分布式UUV集群任务一致性协调SAC算法,如图2和图3所示。

图2 基于改进DDQN的多智能体任务分配算法

Initialize grid mapNumber of initialized UUV clusters M and its coordinatesNumber of initialization task targets N and its coordinatesfor i=1,2,…,M do Assign tasks (Algorithm 1, objective function is Formula 9 and 10)end for# All UUV individuals start executing taskswhile(There are unfinished tasks)All UUV individuals move one step at a time for m=1,2,…,M do if New task received do: Reassign the new task queue (Algorithm 1, the objective function is Formula 21) end if if The same task exists with the task sequence of other UUVs within the detection range do: Reassign tasks after consistent coordination (algorithm 1, objective function is formula 21) end if end forend while

由于每个UUV个体进行任务分配时的UUV数量m和任务数量n不同,在训练过程中根据不同的m和n自适应调整神经网络的输入和输出神经元数量。算法通过设置一个网络库,将训练好的神经网络存入其中,在后续的训练中可以在网络库中找到相同m和n的网络,并在网络参数基础之上继续训练,可以缩减训练所需时间。

图5 UUV-1分配结果及奖励曲线图Fig.5 UUV-1 Distribution results and reward

3 仿真与分析

3.1 环境设置

设置17*17的栅格图模拟水域(单位:km),均匀布置4个UUV在水域内,编号按照从左至右从上至下排序依次为UUV-1、UUV-2、UUV-3、UUV-4。每个UUV的探测范围为以自身为圆心、半径为6单元格的圆,模拟随机出现了10个任务目标点,如图4所示。

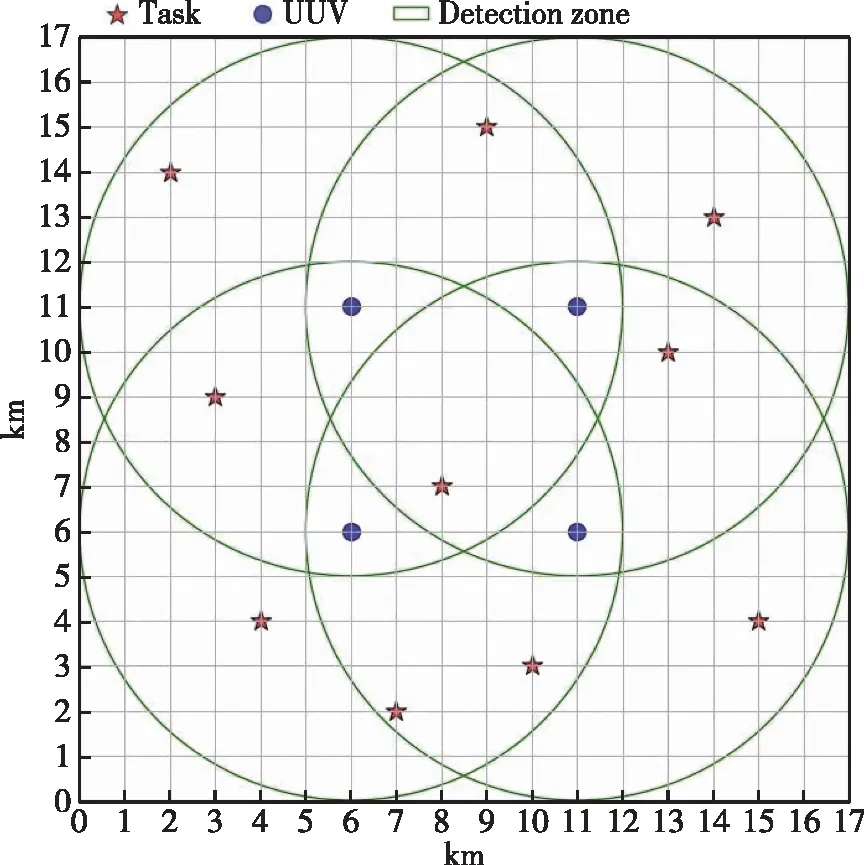
图4 分布式UUV集群任务场景模拟图Fig.4 Distributed UUV cluster task scenario simulation

本文的深度强化学习算法训练部分有超参数如表1所示。

表1 基于改进DDQN的多智能体任务分配算法超参数表Tab.1 Material parameters of the experimental article

3.2 仿真结果

1)UUV个体数量为4 ,任务数量为10 。

根据任务场景设置,图5至图8分别是UUV-1至UUV-4经过算法1的局部任务分配结果图及其奖励收敛曲线图,图9是4个UUV个体经过算法2的UUV集群任务分配结果及其与全局遗传算法分配结果对比图。

如图5所示,左图为UUV-1对其探测范围内的UUV和任务进行任务分配的结果,右图是算法在训练时的奖励收敛图,可以看到智能体在学习了20个完整的分配过程样本后其奖励完成了收敛,并达到了左图的分配效果。图6至图8同理。

图6 UUV-2分配结果及奖励曲线图Fig.6 UUV-2 Distribution results and reward

图7 UUV-3分配结果及奖励曲线图Fig.7 UUV-3 Distribution results and reward

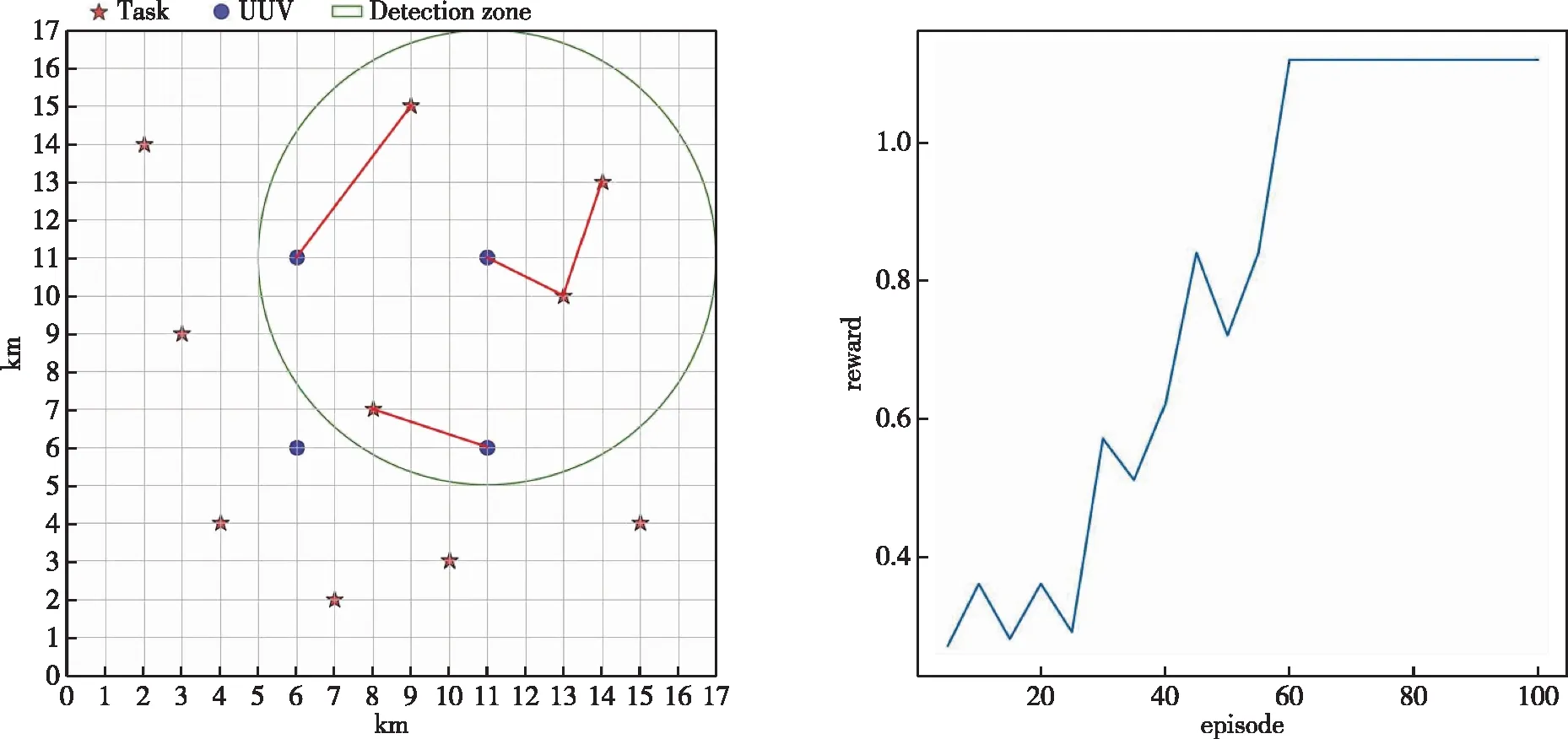
图8 UUV-4分配结果及奖励曲线图Fig.8 UUV-4 Distribution results and reward

一致性协调算法后,UUV集群全局任务分配结果如图9所示。

图9和图10为本文算法和全局遗传算法的分配结果对比图,本文算法分配结果的效用优于全局遗传算法,同时更适合于水下无人平台的任务分配问题。

图9 本文算法分配结果图Fig.9 Thesis algorithm

图10 全局遗传算法分配结果图Fig.10 Global genetic algorithm

2)UUV个体数量为4 ,任务数量为18

增加任务数量至18后,经过算法1和算法2的UUV集群任务分配结果如图11所示。

图11任务中,任务分配可行解的数量为418*18!,这是一个非常庞大的解空间,使用本文算法可以在18秒收敛至优化分配结果。

图11 UUV集群任务分配结果图Fig.11 UUV cluster task assignment

3.3 DDQN算法与改进DDQN算法对比

图12可以看出改进DDQN算法更加稳定和不易震荡,并且可以更快地收敛。本文提出的改进DDQN算法,在动作选择阶段增加了概率下降动作选择策略,这使得智能体可以在庞大连续的状态动作空间里更有机会去尝试那些不是当前最优但可能是潜在最优的动作,这使得智能体的学习过程更加稳定[17],网络可以更快收敛,并且寻找到最优动作的概率显著增加。

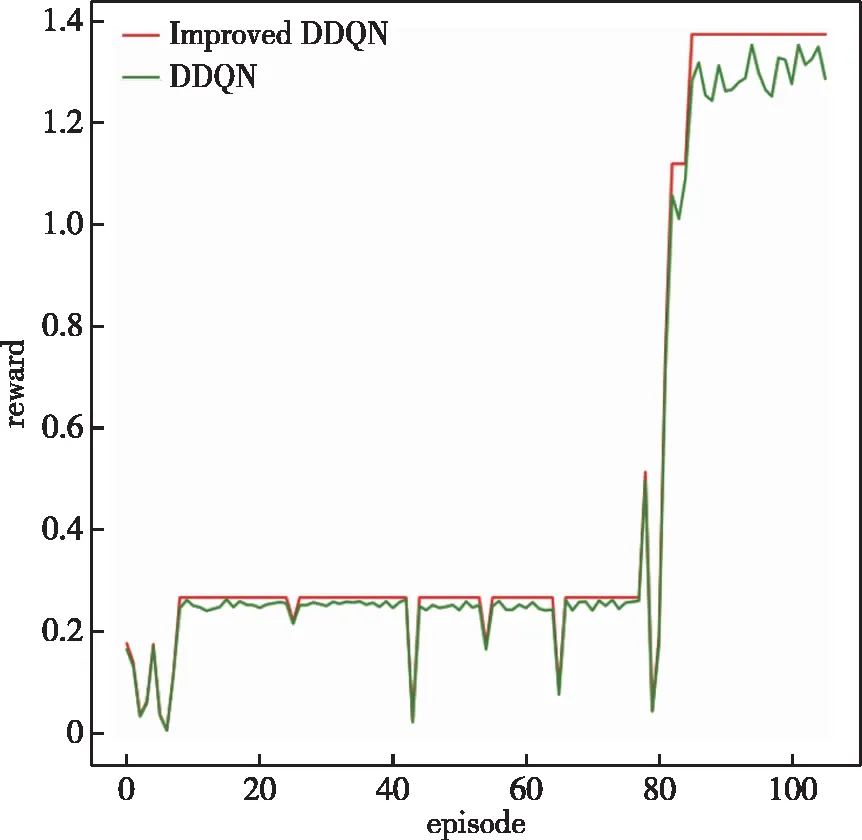
图12 训练奖励对比图Fig.12 Comparison figure at training

3.4 集中式UUV集群全局任务分配算法与本文算法对比

图13对UUV=4、TASK=10、UUV=4、TASK=20、UUV=8、TASK=50时本文提出的算法与全局任务分配遗传算法[18]进行对比,在相同的UUV和任务数量下,本文提出的算法与全局遗传算法优化至相同目标函数值最大值时,收敛时间大大减少。

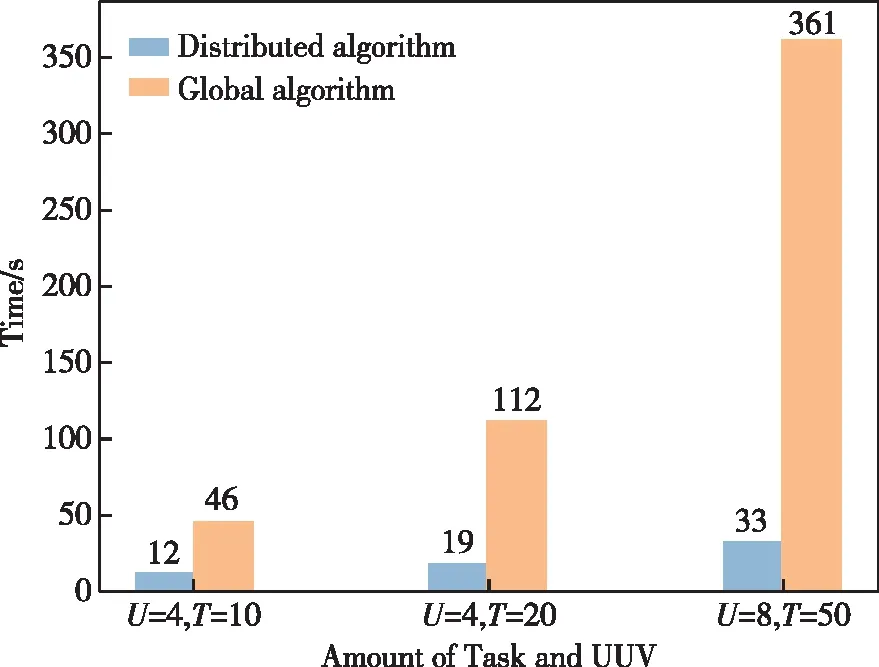
图13 求解时间对比图Fig.13 Convergence time comparison

4 结束语

本文针对水下UUV集群的任务分配问题,考虑UUV通信和探测能力的限制,UUV只能在水声范围内进行通信,其探测范围也受主被动声呐限制,提出了一种分布式UUV集群组织架构,并在此基础上提出了一种基于深度强化学习的分布式UUV集群法。

仿真实验结果说明,该算法成功实现了UUV个体在仅获得局部信息的情况下能够完成对UUV集群的全局优化任务分配。本文算法利用深度强化学习、分布式组织架构的优势和提出的二次分配一致性算法,在达到与传统的全局算法相同优化指标的情况下,算法收敛时间提升了60%以上,并且随着任务复杂度的上升,收敛时间的提升更加明显,本文提出的算法可以有效解决在分布式UUV集群的任务分配问题。