基于遗传算法的交叉定标基准载荷轨道优化方法

史树峰，武海雷

上海航天控制技术研究所,上海 201109

1 引言

卫星遥感技术是通过快速、大面积对地观测以获取地球资源信息的重要手段，随着社会信息化建设的发展，对遥感信息定量化的要求也不断提高。在遥感卫星的管理方面，对星上传感器的定标是保证遥感信息准确性的重要工作。卫星在发射前会进行实验室地面定标，但传感器的性能会随着卫星的在轨工作发生变化和衰减。因此为保证数据质量，需要定期对传感器进行在轨辐射定标（孙立微，2018）。

在轨辐射定标方法大体包括星上定标、场地辐射定标以及交叉辐射定标。星上定标要求传感器配备有星上定标系统，但是成本和代价较高，因此大多数小型卫星在设计上并不支持这种定标方式（张孟 等，2019）；场地定标法通过大量的地面试验和测量，测定卫星过境时刻的地面定标场辐射数据来进行定标（韦玮，2017）。由于需要耗费大量人力物力，所能提供的定标数据比较有限（吕佳彦 等，2017）；交叉辐射定标是使用已知定标精度较高的传感器作为参考，对待定标传感器进行定标的一种方法。其优点是定标成本低，可以实现高频次、多传感器间的辐射定标（高彩霞 等，2013）。

交叉定标的实施方法是：将待标定的在轨卫星传感器作为目标载荷，将已知定标精度高的在轨卫星传感器作为基准载荷，当目标载荷与基准载荷同时（或接近同时）观测同一目标时，就可以用基准载荷来定标目标载荷（王敏 等，2014）。如中巴卫星数据就曾利用中分辨率成像光谱仪MODIS（Moderate−resolution Imaging Spectroradiometer）数据进行交叉标定（张勇 等，2006）。这种方法的优点是不需要精确的大气测量，但对参考传感器的定标精度要求比较高。

因此交叉定标是一种相对便捷的在轨辐射定标方法。实施交叉定标的前提是对遥感卫星轨道进行精准的预测，以便获取基准载荷卫星和目标载荷卫星交叉期间的定标数据。简化常规摄动模型SGP4（Simplified General Perturbations）是由北美航天国防司令部Norad 开发的一种卫星预报模型，能够快速精确预报一段时间的卫星运行轨迹，并且基于美国对卫星的长期跟踪进行轨道数据更新，可以认为有足够的可靠性（刁宁辉 等，2012）。Roithmayr 等利用SGP4 模型进行轨道交叉的研究，将极轨卫星CLARREO 作为基准卫星与JPSS、Metop 卫星的交叉频次进行分析（Roithmayr等，2014）。

在今后有大量遥感卫星定标需求的情况下，有必要设计一种寻找基准载荷卫星轨道的方法，让基准载荷可以最大限度地服务于遥感卫星的定标工作。基于性能良好的轨道预报方法，可以分析影响遥感卫星交叉定标频次的各种影响因素，继而突出最主要的交叉定标频次影响因素，针对性地进行基准载荷轨道优化。

2 交叉定标的轨道交叉模型

2.1 轨道表达与轨道预报模型

卫星在地心赤道惯性坐标系的空间位置和速度问题可用6个轨道根数描述卫星在空间中的运动特性，即卫星的向径r和速度v可以表达为6 个轨道根数的函数。

卫星的空间位置与轨道六根数（半长轴a，偏心率e，轨道倾角i，升交点赤经Ω，近地点幅角ω和真近点角θ）是一一对应的，即已知卫星在赤道惯性坐标系下的空间位置和速度可以得到卫星的轨道六根数，而已知卫星的轨道六根数，也可以获得卫星在赤道惯性坐标系下的位置和速度。

轨道预报的实现是建立在轨道模型构建的基础上，利用卫星轨道两行数，建立基于SGP4 解析轨道模型的辐射基准卫星和待定标卫星的轨道，计算出Δt时间段内，辐射基准卫星的实时空间位置向量和待定标卫星的实时空间位置向量。

2.2 星间交叉定标模型

基本的星间交叉定标模式只要求基准卫星和目标卫星在很短的时间范围内通过相同的星下点，由于严格地控制了两星相交于某星下点的时间差，因此两星能够在相近的辐射条件下对同一地面目标进行辐射定标分析。

已知基准载荷和目标载荷的轨道根数，可以得到基准载荷星下点的地理经度λb、地理纬度φb以及目标载荷星下点的地理经度λt和赤纬φt，由于两星的星下点经纬度轨迹为连续闭合曲线，所以两星每圈运行轨道都会出现星下点交点，但只有两星运行到交点的时间差小于最大时间阈值Tε的情况才是满足定标要求的交叉点。

则基准载荷与目标卫星的星间交叉定标频次N1即单位时间内满足交叉时间间隔约束的观测次数。

2.3 地面固定点交叉定标模型

基本的星间交叉定标模式单纯限定交叉的时间间隔，对于交叉点的地面位置不做要求，对于太阳同步轨道一类的遥感卫星，交叉点往往出现在两极附近，有可能不符合交叉辐射定标要求。

因此结合交叉定标与场地辐射定标方法，针对地面特定定标场进行交叉定标任务设计，能够提供更精确的辐射定标信息。地面固定点交叉定标要求基准载荷和目标载荷对地面特定定标场进行观测，为了避免观测时间差导致的定标场辐射条件差异过大，两星对同一定标场观测的时间间隔要小于最大时间间隔阈值Tε。

为了判定载荷轨道星下点经过地面定标场，假设如图1 定标场为S，载荷轨道高度为h，对地覆盖的观测半锥角为α，根据几何关系，可以确定对应的地心角β满足关系

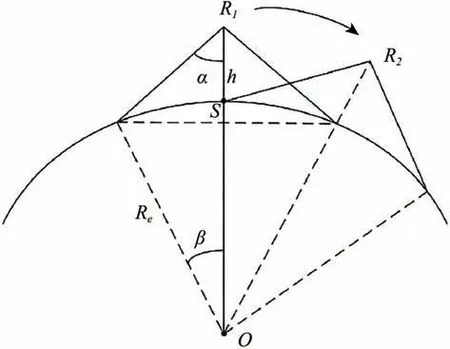
图1 载荷对地面固定点观测的几何关系Fig.1 Geometric relationship of observation between the payload and the fixed ground site

求解得到的β即为定标场矢量OS与载荷矢量OR（OR1或OR2）的最大夹角，然后通过经纬度的球面三角得到定标场经纬度与载荷轨道星下点经纬度的最大偏差

式中，(λS，φS)为定标场S的经纬度，(λR，φR)为载荷轨道星下点经纬度。

通过式（2）能够截取卫星载荷对任意定标场的过顶时间，进一步比对时间轴上目标载荷、基准载荷对同一地面定标场的可观测时间段，如果两组时间段中心值相差间隔小于时间差阈值Tε，则成立一次对固定点交叉定标，如图2。通过统计试验时间段内所有满足时间约束的交叉定标事件，可以得到固定点交叉定标频次。

图2 固定点交叉判定示意图Fig.2 Determination Schematic of fixed site cross

需要注意的是，图1中所示几何关系主要是为了快速筛选经过地面观测点的轨道段，实际上满足几何条件的基准载荷和目标载荷对同一地面点观测的角度并不完全一致，会对定标精度产生影响。在时间间隔Tε较小情况下，可认为这段时间内光照条件相近，所以沿卫星轨道运行方向（迹向）的角度差对定标影响不大；而垂直于卫星轨道运行方向（侧向）的角度差则始终对定标精度有较大影响。因此为了保证具体任务场景的定标精度，在截取可观测时间段时，可以在时间约束Tε之外，根据定标要求对地面定标场观测的侧向偏差额外增加角度约束，加强对有效交叉时段的筛选。

3 交叉定标频次的影响因素分析

在得到两种定标模式的轨道模型的基础上，希望分析影响交叉频次的主要因素，以便于之后进行基准轨道的优化。根据陈轩等（2020）的研究结果，影响交叉频次的仿真条件因素主要包括仿真周期长度T、时间间隔阈值Tε以及固定点交叉定标中的载荷观测角α，这是在特定基准载荷轨道和目标载荷轨道条件下得出的结论。为了得到具有更优性能的基准载荷轨道，还需要探究固定仿真条件情况下，改变基准载荷轨道的参数，对定标交叉频次的影响。

由于卫星轨道一般使用轨道6 要素（a、e、i、Ω、ω和θ）进行描述，我们希望通过固定变量法探究轨道6 要素各自对交叉频次的影响。6 要素中轨道半长轴a与轨道高度h关系为a=Re+h，其中Re为地球平均半径。选定风云−3C 作为目标轨道不变，自定义基准轨道参数，每次仿真取基准轨道的一个轨道要素作为变量改变其取值，仿真分析该轨道要素对交叉频率的影响程度，如表1所示。其中轨道高度h的取值范围为400—2000 km，偏心率e取值范围0—0.08，轨道倾角i取值范围0—180°，升交点赤经Ω取值范围0—360°，另外由于轨道大多数都是近圆轨道，近地点幅角ω和真近点角θ共同决定卫星在轨道上的相位，因此用纬度幅角u=ω+θ进行统一仿真，取值范围0—360°。

表1 交叉频次仿真轨道根数Table 1 Orbital Elements of cross frequency simulation

如图3，仿真得到5 个轨道根数改变时，各自对交叉频次影响，影响程度用最大频次/最小频次的频次比率进行衡量，5 个轨道根数h、e、i、Ω、u在取值范围内的频次比率分别为∞、1.06、1.03、1.26、1.24。可见交叉频次受轨道高度影响程度最大，受升交点赤经和纬度幅角影响显著，受偏心率和轨道倾角影响较小。从轨道交叉规律方面解释这一现象，不同轨道投影到地面的星下点轨迹必然每圈都会有交叉，但只有满足时间间隔约束的交叉才是有效的，这其中卫星运行的周期和轨道相位对交叉的影响作用最大，而恰恰轨道高度、升交点赤经、纬度幅角与卫星的运行周期和相位关系密切，而轨道倾角和偏心率影响微弱。

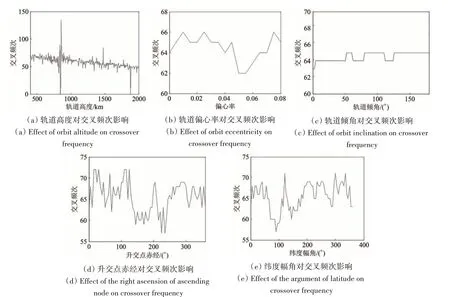
图3 各轨道要素对交叉频次影响仿真结果Fig.3 Simulation results of the effect of each orbit elements on the crossover frequency

这其中还有一种特殊的轨道关系，即基准轨道和目标轨道的高度、升交点赤经接近，两星处于接近相同的运行状态。如图4，在轨道高度接近目标轨道高度时，交叉频次处于极值状态（极大值或接近0），此时两星近似于固定相位差的相伴运行。当两星的半长轴和升交点赤经都相近时，极值的程度也更大，此时相当于两星在同一轨道的不同相位上。虽然实际造成交叉频次很高，但这种特殊情况在轨道设计时是应该尽量避免的。

图4 轨道半长轴和升交点赤经对交叉频次影响仿真Fig.4 Simulation of the effect of orbital semi−long axis and ascending intersection equinox on the crossover frequency

对于固定点交叉定标模式，轨道参数的影响也基本相同，只是由于限定了地面定标场位置，相应的交叉频次都比星间交叉定标要少。在计算交叉频次时，为了保证定标精度，除了考虑地点和时间间隔的匹配，还要考虑基准载荷与目标载荷传感器观测角度的匹配，可以利用观测角度差对交叉情况进行进一步约束。

4 交叉定标基准载荷轨道优化方法

对于交叉定标任务而言，希望基准载荷可以性能良好地服务多个目标载荷，因此要求基准载荷轨道具有更优秀的交叉定标特性。从前面影响因素分析可知，基准载荷轨道优化主要考虑轨道高度、升交点赤经、纬度幅角3 个因素，而且从图3可知，交叉频次具有强烈的局部最优特性，一般非线性优化算法很难求解这类问题的最优解，因此考虑使用遗传算法对交叉频次进行优化。

遗传算法是最先由Holland（1975）提出的一类模拟进化的算法，它源于进化论和群体遗传思想，通过模拟生物进化的遗传机制来求解极值问题。后来经过不断完善和发展，广泛应用于自动控制、计算科学等领域，适用于解决复杂的非线性和多维空间寻优问题（葛继科 等，2008）。

遗传算法优化的流程如下：第1步，以相邻两个阵元的距离的差值作为个体，产生初始种群；第2 步，对每个个体的基因进行从小到大的排序，然后变换到距离间隔种群；第3步，计算每个个体的适应度，判定其是否满足种植准则，如果满足则计算结束，输出最优个体为优化结果，如果不满足，则对中间种群的个体进行选择、交叉、和变异的遗传操作，再重复第1 步和第2 步，一直循环达到终止条件，流程图如图5所示。

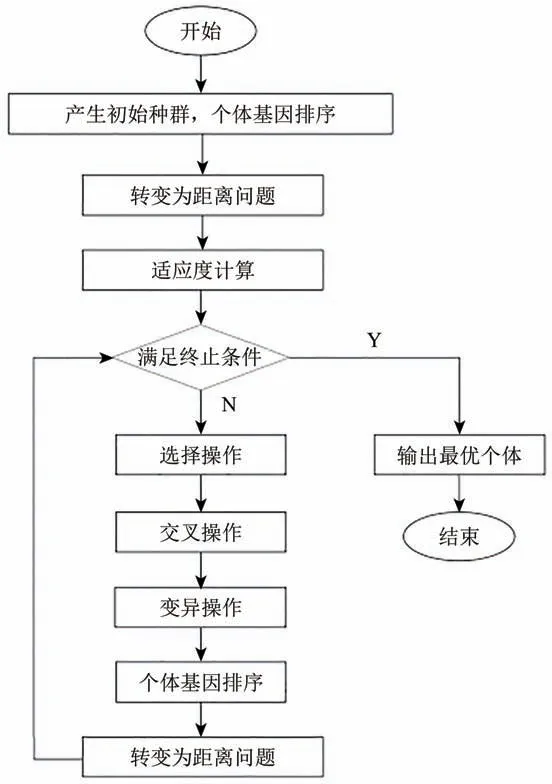
图5 遗传算法流程图Fig.5 Flow chart of genetic algorithm

4.1 星间交叉定标基准轨道优化

构建仿真场景：对多个目标载荷轨道进行交叉定标服务，目标载荷轨道包括：海洋−1B、环境−1A、环境−1B、资源1−2C、风云−3A、风云−3C。

选择两个经典遥感卫星作为优化前的基准载荷轨道：TERRA、NOAA 20，分别与优化后的基准载荷轨道的交叉频次进行对比。

构建遗传算法目标函数x=(a，Ω，u)，即h轨道高度、Ω升交点赤经、u纬度幅角。适应度函数

式中，ncrossi，i=1，2，…，6 为基准载荷轨道分别与各目标载荷轨道的交叉数，适应度函数f使得对6 个目标载荷中交叉频次最小的那个取最大值，这样可以保证基准载荷对所有6个目标载荷都有良好的交叉特性。

仿真周期取30 d，交叉的时间间隔阈值Tε=6 min。遗传算法的运行参数选择，种群规模为50，经过15 代遗传迭代，得到适应度逐渐趋于稳定，优化过程的适应度变化如图6所示，优化后的轨道参数如表2 第3 行数据，相比优化前基准载荷轨道，轨道高度值明显降低。

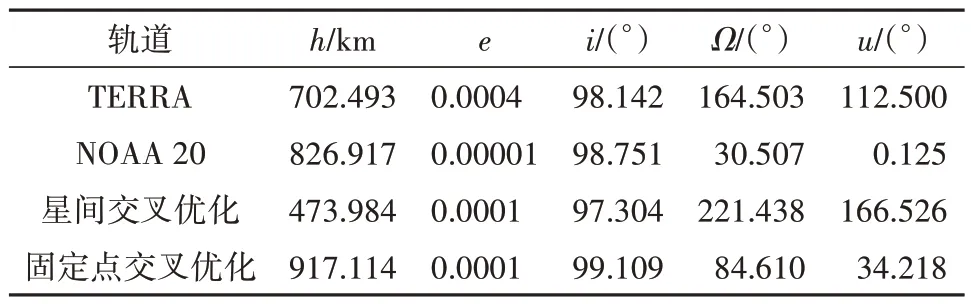
表2 交叉定标优化的轨道参数对比Table 2 Comparison of optimized cross-calibration orbital parameters

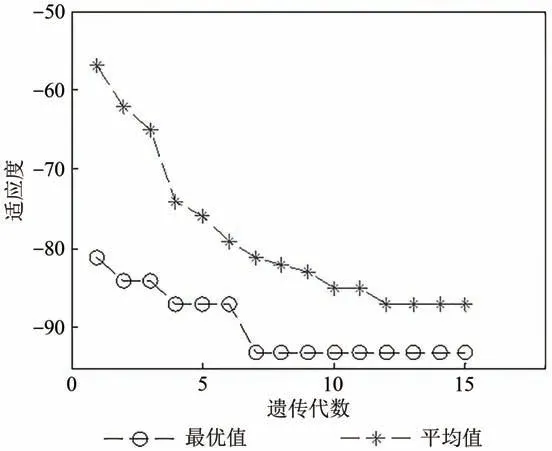
图6 遗传算法代际适应度值Fig.6 Genetic algorithm intergenerational fitness values

如图7，比较TERRA、NOAA 20 和优化轨道的交叉数值，可见优化后的轨道对各目标载荷的交叉频次较为均匀且整体交叉频次有所提高，排除了轨道相位关系引起的交叉点极值情况，经过遗传算法优化后的基准载荷轨道交叉性能得到了明显提升。

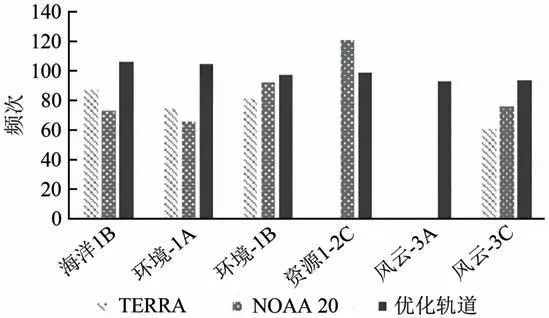
图7 基准载荷轨道优化前后交叉频次对比Fig.7 Crossover frequency comparison before and after reference payload orbit optimization

4.2 地面固定点交叉定标基准轨道优化

构建仿真场景：选取5 个地面定标场（敦煌、阿拉善盟北、美国Railroad Valley、英国Barton Bendish、利比亚），对6个目标载荷（海洋−1B、环境−1A、环境−1B、资源1−2C、风云−3A、风云−3C）进行地面固定点交叉定标，参照基准载荷轨道为TERRA、NOAA 20，将与优化后轨道的交叉频次进行对比。

构建遗传算法目标函数x=(a，Ω，u)，即h轨道高度、Ω升交点赤经、u纬度幅角。适应度函数

式中，ncrossi，i=1，2，3 …，6为基准载荷轨道分别与各目标载荷轨道针对所有地面定标场的交叉数，适应度函数f即为对各目标载荷交叉频次的调和平均数，这样可以保证基准载荷优化结果不会坍缩到某一个目标载荷的相近轨道上，能保证对所有目标载荷都有良好的交叉特性。

仿真周期取30 d，交叉的时间间隔阈值Tε=45 min，设定载荷对地观测的半锥角为35°（出于简化考虑，本例中未对轨道交叉的侧向偏差做更严格的约束）。遗传算法的运行参数选择，初始种群规模为50，经过32 代遗传迭代，得到适应度逐渐收敛稳定，优化过程的适应度变化如图8 所示，优化后的轨道参数如表2 第4 行数据，相比优化前基准载荷轨道，其轨道高度值明显增大。

图8 遗传算法代际适应度值Fig.8 Genetic algorithm intergenerational fitness values

如图9，比较TERRA 和NOAA 20 与优化轨道的交叉数值，可见优化后的轨道对各目标载荷的地面固定点交叉定标频次有了明显增加且分布较为均匀，避免了对部分轨道交叉特性不良的现象。经过遗传算法优化后的基准载荷轨道交叉性能得到了明显提升。

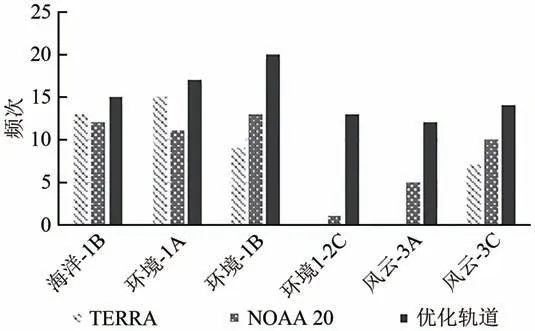
图9 基准载荷优化前后交叉频次对比Fig.9 Crossover frequency comparison before and after reference payload optimization

5 结论

空间辐射交叉定标旨在通过构建高精度的辐射基准传递，突破现有遥感卫星在轨绝对辐射定标精度和定标频次不高的问题。本文利用轨道精确预报方法和交叉定标轨道交叉模型，结合交叉频次影响因素分析结果，提出一种适用于遥感卫星定标的基准轨道设计方法。研究发现，影响两种交叉定轨模式交叉频次的主要轨道要素是轨道高度、升交点赤经和纬度幅角3个因素。因此基准载荷优化主要考虑对这3 个要素作为目标进行优化，将优化变量缩减到3 个，大大减小了计算难度，而遗传算法的使用也解决了交叉频次优化容易陷入局部解的问题。通过仿真验证，对两种交叉定标模式进行遗传算法优化后，基准载荷的交叉定标性能都有了明显的提升。