大观念视角下数学单元整体教学探索

徐琳

【摘要】大观念视角下的单元设计指向数学核心素养，同时也是新教学典型特征之一.本文以AP统计教学单元为例，从提炼单元结构、规划单元教学目标、实施单元教学三个方面，结合已有的案例与经验，阐述在大观念下数学单元整体教学方面的探索，旨在为同行教师开展高中数学单元教学提供参考.

【关键词】高中数学；单元设计;大观念视角

在新课程改革的背景下，新教学的需求和理念为高中数学教学实践的改革指明了方向.而素养本位的单元设计正是新教学的典型特征之一.

以课时为单位的数学教学易使学生的知识割裂，不利于形成一个完整的知识链条和结构体系，而单元教学设计倡导将教学内容置于单元整体内容中去把控，以突出数学内容的主线以及知识间的连贯性，从而提高教学效率，更多关注教学内容的本质、蕴含的思想及学生素养的培养.

大观念视角下的数学课程可以代表数学的核心概念，大观念的理解与应用直接体现了数学核心素养的要求，同时大观念视角下的单元课程能有效地组织起零碎化的知识与技能，帮助学生真正理解数学概念本质，发展学生的整体观和结构观.

本文将以AP统计教学单元为例，从提炼单元结构，规划单元教学目标，实施单元教学三个方面，阐述在大观念下数学单元整体教学方面的探索.

1 提炼单元结构

学科大观念是指学科具体知识背后的隐形的本质内容.教师在设计单元整体教学时，应综合考虑单元各节内容所要表达的意义并发现其关联，从育人的角度思考单元内容对学生成长的价值和意义，以此来确定单元大观念.以AP统计中线性回归、置信区间、假设检验为例进行单元整体教学，在教学设计过程中可以借助结构导图帮助学生串联起单元的知识结构，理清本质的逻辑联系.

1.1 线性回归

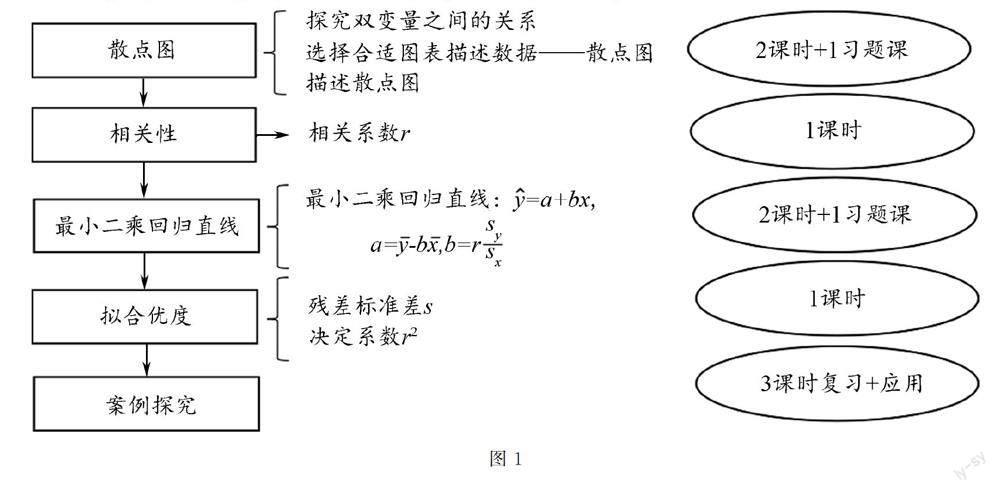
线性回归通常是在学习数据、图表及其相关描述性统计量章节后的单元.单元教学设计的目的是让学生类比已学过如何分析单变量的分布以及描述后，进阶到利用类似方式描述双变量之间的关系，同时本章内容也可以结合数学中一次函数的相关定义帮助理解线性回归的相关统计量和参数.内容安排如图1所示.

1.2 置信区间

在单元设计中，以构建置信区间整体思路为线，串联起对不同参数的区间估计.内容设计如图2所示.

通过构建单元结构图，可以看到不同知识点与案例之间的关系与意义，从而深入了解知识背后的深层含义，能帮助学生建立大观念的知识体系，对知识有相对完整的认知，在学习中起到提纲挈领的作用，让单元不再是知识点的叠加，而是工具性与科学性的有机结合.

2 规划单元教学目标

2.1 线性回归

结合单元大观念和单元内容，制定本单元教学目标为：

2.1.1 学科知识

（1）掌握散点图描述双变量之间的关系，并能描述其性质；能够通过相关性统计量进行量化，并能阐述其不同情况下的含义.

（2）理解推导回归方程的基本思路，掌握回归方程的系数y=ax+b，a=SxySxx，y-=ax-+b，并用于估值，能够通过不同统计量理解拟合优度.

2.1.2 学习能力

（1）学生能够从定性和定量不同方面描述变量之间的关系，并能找到合适的统计量进行数据支持.

（2）学生会熟练使用最小二乘回归方程进行拟合运算，并利用函数进行估计.

2.1.3 学科素养

培养学生化归转化的思想和基本的抽象总结的能力.鼓励学生面对和克服困难.

2.2 置信区间

2.2.1 学科知识

掌握构建置信区间的一般方法；能够计算点估计和临界值，理解统计量样本分布的均值和标准差.

2.2.2 学习能力

能够根据置信区间公式构建单样本均值和双样本均值的置信区间；构建单样本比例和双样本比例的置信区间.

2.2.3 学科素养

培养学生数据分析和数学建模的能力，以及结合实际问题的能力.

3 实施单元教学

大观念的获得和理解，是在不断解决问题的过程中发生的.因此，教师要基于单元目标开发问题和学习活动，帮助学生形成以大观念为统摄的知识结构，形成能迁移到实际问題中解决实际问题的能力，以及对实现自我和社会新的认知、态度和价值观.

3.1 案例分析

以随机变量的变换为例，设置以下问题；

以点图为班级学生身高，单位是厘米（cm）.

（1）如果班级学生都站在40cm的椅子上，测量学生头顶距离地面的高度，此时新的分布与原身高分布相比，形状、中心和分散度如何变化？

（2）假如我们将班级所有的高度单位从厘米改为英寸（1cm=0.394inch），试着描述一下此时分布的形状、中心和分散度.

设计意图 复习已学过数据变化对分布的影响.类比到变量经过线性变换后对概率分布的影响.这部分较容易推出，也相对容易理解，在复习的同时对线性变换后概率分布变化进行总结.

3.2 数学建模

以线性回归为例：

设计意图 在基于单元教学设计中，设计相关建模问题，一方面以真实情境与任务背后的“真实世界”直接作为课程的组成部分，以实现学生的“真学习”；另一方面，通过让学生做事，考查学生所学的知识，检验核心素养的落实.教师可将建模过程以问题串形式分解，引导学生解决问题，从而完成建模.

参考文献：

［1］崔允漷.新时代  新课程  新教学［J］.教育发展研究，2020，40（18）：3.

［2］姜启源，谢金星，叶俊.数学模型（第四版）［M］.北京：高等教育出版社，2011.1.

［3］崔洪喜.大观念视角下的小学数学单元整体教学［J］.天津教育，2022（23）：21-23.

［4］马丽平.小学数学单元整体教学研究［J］.教学管理与教育研究，2022，7（14）：91-92.

［5］杨明媚.跨越盲区：重构小学数学单元整体设计［J］.中国教育学刊，2022（05）：92-95.