新型电力系统全息电流采样值差动保护仿真研究
2023-06-09宋小舟伍叶凯杨卉卉屠黎明肖正强刘怀宇
宋小舟,伍叶凯,陈 昊,杨卉卉,屠黎明,肖正强,刘怀宇
(1.北京四方继保工程技术有限公司,北京 100085;2.北京四方继保自动化股份有限公司,北京 100085;3.国网江苏省电力有限公司南京供电分公司,江苏 南京 210019;4.国网江苏省电力有限公司超高压分公司,江苏 南京 211102)
0 引言
新型电力系统风力发电[1-2]、光伏发电[3-5]规模持续扩大,特高压直流输电[6-8]和柔性直流输电[9-13]快速发展,电力电子器件的应用达到前所未有的规模。电力系统的电源结构由可控连续出力的煤电装机占主导,向强不确定性、弱可控出力的新能源发电装机占主导转变;负荷特性由传统的刚性、纯消费型,向柔性、生产与消费兼具型转变;电网形态由单向逐级输电为主的传统电网,向包括交直流混联大电网、微电网、局部直流电网和可调节负荷的能源互联网转变[14-17];技术基础由同步发电机为主导的机械电磁系统,向由电力电子设备和同步机共同主导的混合系统转变;运行特性由源随荷动的实时平衡模式、大电网一体化控制模式,向源网荷储协同互动的非完全实时平衡模式、大电网与微电网协同控制模式转变。
电力系统的转变导致电力潮流随新能源出力波动而大幅变动,甚至双向流动,分布式新能源也会改变电力潮流。电力电子元件的普及程度不断提高,特性不一,导致电力系统继电保护越来越难以用现有的传统理论解释与分析[18-23]。在柔性低频输电系统,即如图1 所示,由于系统频率的降低和大量电力电子元件的接入,换流器的短路电流承受能力有限,低频系统发生故障时,对保护速动性和抗谐波能力,较传统的继电保护要求更高,传统基于工频量的交流保护原理将不再适用[24]。

图1 双端柔性低频输电网络示意图Fig.1 Diagram of two-terminal flexible low-frequency transmission network
传统电力系统故障电流的谐波含量较低,继电保护主要考虑50 Hz 的故障电流,一般忽略谐波故障电流对动作特性的影响。在新型电力系统中,大量电力电子器件的应用,谐波故障电流含量大幅增加,与频率无关的包含谐波电流的保护原理更能反映故障的特性[25],因此,本文提出基于全息电流的采样值差动保护原理,开展采样值差动保护在新型电力系统的适应性研究,具有较强的现实意义。
全息故障电流是指包含50 Hz 故障电流、直流暂态分量电流、各次谐波(非整次)电流等全部故障信息的电流,基于全息故障电流的采样值差动保护原理既是对原有采样值差动保护原理的继承,也是对采样值差动保护原理适应性的拓展。
1 全息电流采样值差动保护基本原理
目前微机型继电保护原理通常采用傅氏算法计算电流的有效值,这是对模拟式电流继电器的差动保护原理的继承。基于一个周波时间窗的算法反应基波分量,无法反应电力系统初始故障时较高含量的非基波分量。这在较长时间内影响计算的准确性,为了提高保护动作的可靠性将导致保护动作速动性性能的降低。若电流差动保护不仅反应基波分量还能反应非基波分量,同时动作判据基于每一个采样值单独判断,则可以在原理上完全消除上述影响[26-34]。
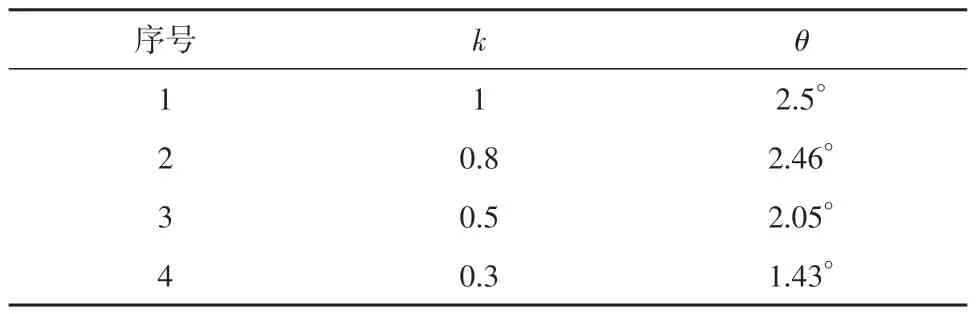
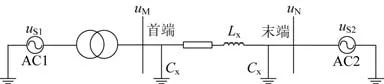
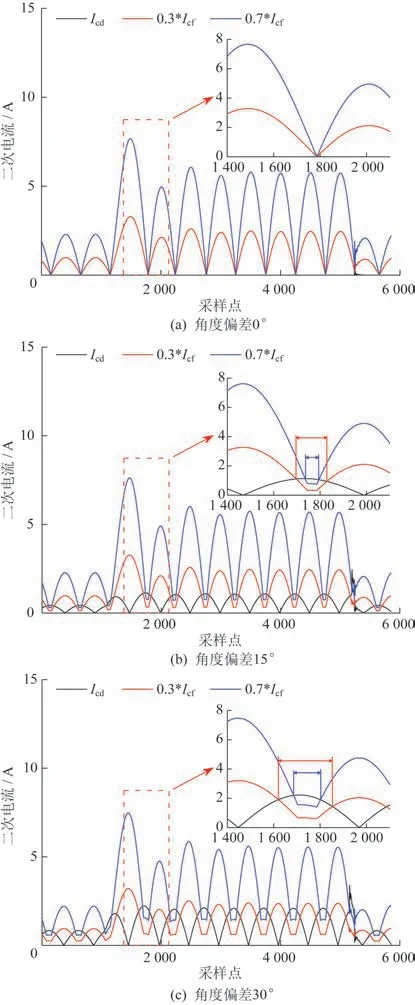
全息电流采样值差动保护首先是对包含50 Hz故障电流、直流暂态分量电流、各次谐波(非整次)电流等全部故障信息的电流进行采样,基于传统电流差动原理对不同采样时刻的全息电流采样值差动的制动关系进行运算,在此基础上采用重复多次判别方法,提高保护动作判据的可靠性[26]。由于全息电流采样值随时间周期性变化,故对每一个采样值而言,其制动关系不一样。为确保采样值差动保护的制动性能不低于常规相量差动保护,半周波判别数据窗对应的角度必须不小于90°。为保证动作判据的可靠性,需要连续r次采样判别中有不少于s(s 为便于与传统采用相量差动的母差保护精度进行对比,假设故障电流为工频电流,依据母线保护采样值差动原理,全息电流采样值差动可以描述为公式(1),其中C为常数;Ȧ、Ḃ为相量。由文献[26]可知,采样值差动电流的动作范围边界如公式(2)所示。可知公式(1)动作边界范围如公式(3)所示,其中N为每周期的采样点数;A、B分别为相量Ȧ、Ḃ的幅值。 由式(2)、式(3)可知,提高保护装置的采样率可以减小保护动作区边界的不定区域范围,即当N→∞时,这种不确定区域消失;当N=∞时,边界范围下限为C。如图2所示为全息电流采样值差动保护动作边界变化范围。 图2 采样值电流差动保护动作边界变化范围示意图Fig.2 Schematic diagram of action boundary variation range of sampling value current differential protection 将全息电流采样值差动动作边界范围由正弦曲线描述,即如图3所示。当差动电流为正弦量时,假设差动定值为C,差动电流为A,若A=C,差动保护恰好动作,半周波动作范围为90°。由正弦曲线特性可知,差动电流采样值最大值为A,45°角的采样值为A,135°角的采样值为A,两个特殊的角度正好满足采样值动作边界条件A≥C,角度差为90°,正好满足采样值差动性能的要求。理论上不考虑采样误差,差动保护100%正确动作。 如何保证45°和135°两个边界点采样不遗漏,是全息电流采样值差动保护动作的关键,也是其无误差动作的关键。根据公式(2)可知不同采样点N情况下,动作边界误差曲线如图4 所示,其中N为正整数,若N为无穷大,误差为零。 图4 全息电流采样值差动保护动作边界误差曲线Fig.4 Action boundary error curve of holographic current sampling value differential protection 根据全息电流采样值差动保护的边界误差,如果不依赖其它算法的配合,为达到5%精度指标要求,由图4可知每周波的采样点数应不少于72点,接下来将以72采样点为例进行分析。 差动保护是高压设备的主保护,保护的速度性是其重要的指标,各种保护对其速动性都有严格的要求,如母线保护小于15 ms、线路保护小于30 ms(出口短路故障小于20 ms)、变压器保护小于30 ms 等。工频保护周期为20 ms,一般采用全波或半波傅式算法,其精度要求是1 个或半个周波数据窗,时间10 ms ~20 ms,无论幅值算法或采样值算法,都能找到最佳的动作速度满足系统要求。 对于低频系统,如果采用三分频输电,数据窗半周就已经达到30 ms,明显无法适应保护快速性的要求。即使采用全息电流采样值差动算法,根据文献[26]的要求,三分频系统90°动作区间对应的动作速度最快是15 ms,若考虑故障角度的特殊情况,保护的动作速度则无法满足系统要求。 如何满足低频系统可靠性与速度性的双重要求是当前工程应用难题,采样值算法是最佳的选择方案之一,但显然90°动作区的传统采样值算法需要改进。采样值的90°动作区间是最不利的制动系数为1 的情况下得出的结论,现有的保护实际应用时制动系数都比较低,例如母线保护,考虑灵敏度的要求,制动系数一般选在0.3~0.8范围内。 根据文献[27]及图5 分析,采样值差动的误动区如公式(4)所示。对于采样值差动,其动作判据的误判区α≤ π/2,故为保证采样值差动的可靠性,使其制动特性等于或优于常规相量差动保护,判别数据窗对应的角度需满足θ≥ π/2。 图5 id≥id0误判区Fig.5 Zone capable of misjudging by criterion id≥id0 与采用相量算法的差动保护不同,采样值算法差动保护利用每个采样点重复性判别来实现,采样值采集的离散性,使得基于采样值差动保护的瞬时动作电流存在一个模糊区。即存在一个模糊范围[Z1,Z2],当基波电流有效值I>Z1时,采样值差动处于动作区,可靠动作;当I 图6 id≥K*If的模糊区Fig.6 id≥K*If Fuzzy region 若模糊区夹角为θ,设k=tanΦ,结合公式(3),在采样点为72的情况下,可得不同k值情况下夹角θ值,如表1所示,当采样点为72时,差动动作的模糊区和制动系数相关性不大,模糊区夹角不会大于2.5°。采样值差动应用低频系统,如果仍坚持大于90°的动作区间判别,无法满足速度性要求,所以需要从比率制动动作原理重新分析。 表1 不同k值情况下夹角θ值Table 1 Values of θ for different k 母线保护的支路可以简化为输入输出两个支路,电流分别为i1、i2,如果参照比率制动原理,动作方程如公式(5)所示。 假设i1、i2之间夹角为φ,则可知差流如公式(6)所示。为分析方便,假设i1和i2的幅值为1,则制动电流if等于2,可知在不同的φ情况下角度偏差,如表2所示。由表2可知,当制动系数选取不同值时,差动保护对i1、i2之间的角度偏差要求是不同的,当k=0.5 时,要求不大于60°;k=0.7时,要求不大于90°,这估计也是采样值差动要求动作区间大于90°的原因,满足大多数制动系数的要求。对于变压器和线路保护,虽然制动系数的选取方法和母线不同,但道理类似,不同的制动系数对于不同的误动角度偏差,制动系数越大,误动角度范围越小。 表2 不同Φ情况下角度偏差值Table 2 Angle deviation values for different Φ 母线和变压器保护,i1、i2之间的角度偏差不会很大,这是由于其电流回路很近,可认为无角度偏差。对于线路保护,一般100 km 约6°左右,即使300 km 线路角度偏差也不到20°,根据制动系数和误动角度的关系,此时制动系数只要大于0.173 6,保护就不会误动。因而不考虑与常规幅值的比率制动比较,母线保护的采样值动作区间只要大于20°,保护的动作行为就确保可靠,即采样值差动保护动作区间不一定要大于90°。当然,选取制定系数时,还需要适当考虑TA的角度误差以及保护装置里电流变换器(小TA)的角度误差。 基于此,本文提出了基于制动系数可变动作区间的采样值差动方案。其核心思想是,保护判别时,同时应用多个制动系数和动作区间,例如:k=0.3时,动作区间90°,最快动作时间15 ms;k=0.7时,动作区间60°,动作时间10 ms。当故障开始阶段,可以投入快速判据,争取保护10 ms动作,若此时故障较小,可以投入更灵敏的k=0.3制动系数判据,保证保护可以切除故障。基于制动系数可变动作区间的全息电流采样值差动保护,兼顾了保护的动作速度和可靠性,使采样差动能够应用于低频输电系统,并且能够满足现有的保护动作性能指标。 为了验证全息差动原理在低频输电系统应用的可行性,建立如图7 的仿真系统。其中M 侧系统电压等级为110 kV、容量为600 MVA,N 侧系统电压等级为35 kV、容量为40 MV,变压器变比为110 kV/35 kV、容量为60 MVA,系统频率为20 Hz,采样频率为20 kHz。 图7 低频输电差动原理仿真系统图Fig.7 Simulation system diagram of low frequency transmission differential principle 区内B 相故障电压及两侧电流采样如图8 所示,Ub为B相电压,Ib1和Ib2分别为首端和末端电流,录波从采样点1 至9 548,故障时段在采样点2 192 至6 546之间。 图8 线路区内B相故障录波图Fig.8 B-phase fault wave-recording pattern in line area 根据公式(5),计算线路区内B相故障对应的差动电流Ibd和制动电流Ibf,即如图9 所示,其中制动系数k1=0.3、k2=0.7,由图可知区内B 相故障时,故障电流无相位摆动,角度偏差为0°。则按正常定值整定范围[0.3,0.8],不论制动系数为0.3还是0.7,差动电流Ibd在整个故障时间段内均大于制动电流,故障角度无论多少,保护均可靠动作。 图9 线路区内B相故障采样值差动动作行为分析Fig.9 Analysis of differential action behavior of B-phase fault sampling value in line area 区外C 相故障两侧电流采样如图10所示,Ic1和Ic2分别为首端和末端电流,录波从采样点1 到5 938,故障时段在采样点1 170至5 186之间。 图10 线路区外C相故障录波图Fig.10 C-phase fault wave-recording pattern outside line area 根据公式(5),计算线路区外C相故障对应的差动电流Icd和制动电流Icf,即如图11 所示,其中制动系数k1=0.3、k2=0.7。图11(a)中,区外C相故障时,故障电流没有相位摆动,角度偏差为0°。则按正常的定值整定范围[0.3,0.8],不论制动系数为0.3还是0.7,差动电流Icd在整个故障时间段内几乎为0,差动电流小于制动电流,差动保护不会误动。图11(b)中,故障电流角度偏差为15°,由图可知制动系数为k1=0.3 时,差动误动范围为48.2°,k2=0.7,差动电流误动范围为21.2°。图11(c)中,故障电流角度偏差为30°。由图可知制动系数为k1=0.3 时,差动误动范围为83.9°,k2=0.7,差动电流误动范围为41.8°。随着故障电流角度偏差变大,差动误动范围变大。 图11 线路区外C相故障采样值差动动作行为分析Fig.11 Analysis of differential action behavior of C-phase fault sampling values outside line area 线路角度偏差一般不大于20°,上述角度偏差按30°考虑,保留了足够的动作裕度。在角度偏差30°的情况下,按最灵敏的制动系数0.3 考虑,可知差动保护动作角度大于90°则不会误动,能够保证可靠动作。若按制动系数0.7考虑,动作角度大于45°便可保证差动保护不误动。因此可依据不动的保护动作时间及灵敏度要求,通过制动系数的变化制定保护动作策略。 双高电力系统和柔性低频输电系统对保护速动性的要求较高,保护的谐波较传统系统复杂,传统基于工频量的交流保护原理将不再适用。全息采样值差动原理具有动作速度快、抗干扰能力强、无惧谐波等特点,因此,开展全息电流采样值差动保护在双高和柔性低频输电系统的适应性研究,具有较强的现实意义。 本文根据双高电力系统和柔性低频输电系统故障电流的特点,分析了全息电流采样值差动应用在变压器、母线和线路保护的可行性,提出了基于制动系数可变动作区间的全息电流采样值差动方案,通过低频输电系统线路区内、区外故障仿真分析,验证全息差电流采样值差动原理的可行性,为未来全息电流采样值差动保护的工程应用奠定基础。2 全息电流采样值差动保护误差分析


3 全息电流采样值差动保护应用分析



4 全息电流采样值差动保护仿真分析
4.1 区内故障


4.2 区外故障

5 结语
