基于中智理论的大断面隧道工程安全风险评估

高建科 刘少华 高鹏飞 何梁华 李宗恒 李 林

（1.绍兴柯桥杭金衢联络线高速公路有限公司，浙江 绍兴 312000；2.绍兴文理学院土木工程学院，浙江 绍兴 312000；3.绍兴市交通运输行政执法队，浙江 绍兴 312000；4.绍兴市交通工程管理中心，浙江 绍兴 312000）

由于大断面隧道断面面积大、风险系数高，需要进行风险评估，以降低隧道塌方、突水突泥、大变形破坏等事故的概率。国内外学者提出很多隧道风险评估的方法。张永刚[1]等综合运用信心指数法、层次分析法对渤海湾海底大断面隧道进行风险评估；宋平原[2]在前者基础上，利用可拓模型并结合层次分析法对大断面隧道进行风险评估；何乐平等[3]基于博弈论-云模型，提出一种新的云模型综合风险评价方法。在国外，Ou，Guang-Zhao 等[4]提出一种基于D-S 证据理论的风险评估方法，Zhiqiang Wu、C.J.Lin 等[5-6]将正态云模型与熵权法相结合，提出一种新的隧道风险评估模型。

在实际工程中，由于勘测技术有限，无法全面了解整个工程的地质条件、水文因素等，隧道的风险因素就会存在部分确定、部分不确定信息。现有的这些风险评估方法难以表达这些不确定信息，这就会影响隧道风险评估的准确性。基于中智理论，采用中智数正切相似度量法对杨家山大断面隧道进行风险评估，综合考虑隧道风险因素中的不确定信息，提高隧道风险评估的准确性。

1 中智理论的介绍

1.1 中智数的概念

1998 年，Smarandache 将中智学引入数学问题中，由此产生了中智理论，其中包括中智数[7]。中智数是中智理论中十分重要的组成部分，它使该理论能够表达样本数据中不确定的信息。

中智数一般形式表达为U=s+tY，由确定部分s和不确定部分tY组成。例如一个隧道的断面面积在160 m2～180 m2，用区间形式表达为[160，180]。采用中智数表达，假定不确定系数Y∈[0，2.5]，确定c为160，t为8，得到中智数U=160+8Y，Y∈[0，2.5]。

现有2 个中智数U1=s1+t1Y和U2=s2+t2Y，那么中智数的数据基本运算法则如公式（1）所示[8]。

式中：U1、U2为中智数；s1、s2为中智数中的确定部分；t1、t2为中智数中的不确定部分；Y为不确定系数。

1.2 中智数正切相似度量法

相似度量法是一种按照一定的度量准则计算特征信息相似度的计算方法。在中智数运算法则的基础上，引入中智数向量的相似度量计算方法。

假设存在2 个中智数向量A={UA1，UA2，…，UAj}和B={UB1，UB2，…，UBj}，向量中的中智数元素表达为UAj=sAj+tAjY和UBj=sBj+tBjY（j=1，2，…，n）且sAj，tAj，sBj，tBj≥0。实际应用中往往会对中智数元素进行归一化处理，可得UAj，UBj∈[0，1]。

中智数向量A与B的正切相似度量公式如公式（2）所示[9]。

式中：T（A，B）为向量A与向量B的相似度量值；sAj、sBj为中智数中的确定部分；tAj、tBj为中智数中的不确定部分；Y为不确定系数；inf 为集合的最小值；sup 为集合的最大值。

在实际工程应用中，各影响因素的相对重要性是不同的。因此，基于上述中智数正切相似度量公式，引入影响因素的权重值向量K=（k1，k2， … ，kn），kj∈[0，1]，且，得到考虑权重因素下的中智数正切相似度量公式，如公式（3）所示。

式中：Tk（A，B）为向量A与向量B相似度量值；sAj、sBj为中智数中的确定部分；tAj、tBj为中智数中的不确定部分；Y为不确定系数；kj为影响因素的权重值；inf 为集合的最小值；sup 为集合的最大值。

2 评估方法

2.1 评价指标和评价等级的划分

隧道施工中可能遇到的风险众多，影响风险的原因也种类繁多，大致可分为工程地质因素、设计因素和施工因素，见表1。

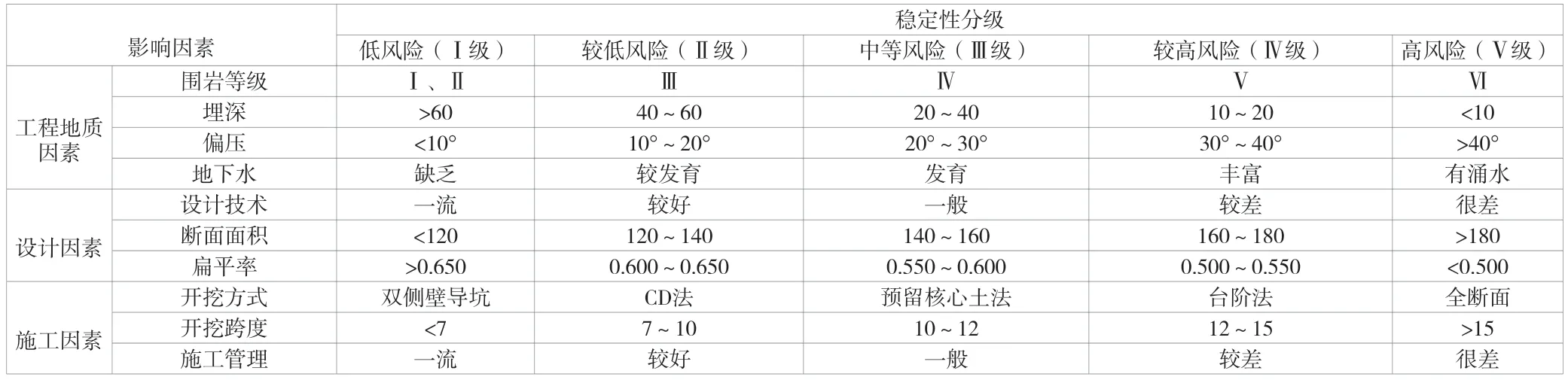
表1 评价指标划分标准

表1 中的围岩等级是按照规范要求，根据岩体完整性、岩体强度等指标划分；隧道埋深越浅越不利于隧道稳定，风险越高；偏压通常可用山体倾角表示，倾角越大，风险越大；地下水情况由地下水缺乏到丰富再到有涌水情况出现，风险等级依次变高；设计技术水平是对设计单位的设计方案的综合考量，对设计的大断面隧道进行针对性研究、对大断面隧道荷载计算方式严谨论证、充分参考相近大断面隧道工程案例、经过专家讨论后的合理科学的设计方案，认为该设计方案是充分的，设计水平为“一流”，缺乏以上步骤的设计方案就按照缺少步骤数依次降低等级；开挖方式按常见的大断面隧道开挖方式进行分级，不在表1 的开挖方式可根据实际效果等效进行评定；大断面隧道的开挖跨度越大，围岩的稳定性越低；施工管理的水平可以从工程技术人员的技术水平、施工技术管理制度以及施工技术设备等方面评价施工企业的施工管理水平，从而划分为不同的档次。

表1 中各影响因素的量纲不同，无法直接进行数学计算。因此，在进行隧道风险评估前，需要通过一定的计算将表1 中的数据归一化到[0，1]。

对定量评价的影响因素（围岩等级、埋深、偏压、开挖跨度、断面面积、扁平率）来说，将评价范围转化为[0，1]，对隧道安全性有良好作用的数据越接近0，对隧道安全性有破坏作用的越接近1，然后按内插法转化各等级数据。对定性评价的影响因素（地下水、设计技术、开挖方式、施工管理），由设计和施工人员根据专业知识和工程经验，在区间中给出数值，以反映该因素的影响程度。

将表1 中的数据进行归一化处理后，得到归一化后的隧道风险因素评价，见表2。

表2 归一化后的隧道风险因素评价表

为了更简单、全面地表达隧道风险因素评价表中的确定和不确定信息，根据中智数原理将评价表中的区间值表达为中智数的形式，即U=s+tY形式。设定不确定值Y∈[0，0.25]，得到中智数形式下的隧道风险影响因素评价，见表3。

表3 中智数形式下的隧道风险因素评价表

2.2 风险因素的权重计算

2.2.1 主观权重的计算

采用层次分析法对大断面隧道同一层次的风险指标进行两两比较，得到判断矩阵C，评判原则见表4

表4 层次分析法评判原则

解特征根问题如公式（4）所示。

式中：C为判断矩阵；λmax为最大特征值；ω为特征向量；特征向量的每个分量即为对应权重。计算向量的方法如下。

计算几何平均值，如公式（5）所示。

计算相对权重，如公式（6）所示。

式中：wi为相对权重值；为几何平均值。

计算最大特征值，如公式（7）所示。

式中：λmax为最大特征值；（Cω）i为向量Cω的第i个元素；wi为相对权重值。

根据矩阵理论，在满足一致性条件的情况下，判断矩阵有且仅有一最大特征根λmax，其值等于n。在实际应用中，判断矩阵会偏离完全一致性，当偏离程度在一定范围内，认为是可以接受的。

首先计算偏离一致性指标，如公式（8）所示。

式中：CI为偏离一致性指标值；λmax为最大特征值。

同时，需要满足随机一致性比例要求，如公式（9）所示。

式中：CR为随机一致性比例值；RI为平均随机一致性指标。

2.2.2 客观权重的确定

采用熵权法分析指标值的差异程度，计算各个指标的权重系数。熵权法充分利用数据中的有效信息量。其具体步骤如下。

2.2.2.1 指标值归一化

取n个样本，每个样本有m个指标，构建原始指标值矩阵X={xij}n·m，对该矩阵的数据进行归一化，如公式（10）所示。

式中：pij为归一化指标值；xij为矩阵X中的元素。

2.2.2.2 计算指标熵值

式中：ej为第j个指标的熵值；pij为归一化指标值。

2.2.2.3 计算指标熵权

式中：vj为第j个指标的熵权值；ej为第j个指标的熵值；m为样本中的指标数目。

最终每个指标的熵权组合得到熵权法因素权重集：

2.2.3 综合权重确定

将层次分析法和熵权法结合，既能表达专家主观赋值的影响，合理利用其丰富的经验，又能遵循样本数据信息的客观数学规律，兼顾主观性和客观性。使用层次分析法得到主观权重集W=（w1，w2，…，wm）以及用熵权法得到客观权重集V=（v1，v2，…，vm）后，根据公式（14）得到综合权重系数集：A=（a1，a2，…，am）。

式中：ai为第i个指标的综合权重；wi为第i个指标的主观权重；vi为第i个指标的客观权重。

2.3 中智数正切相似度量评估法

通过中智数正切相似度量公式（3），计算隧道样本S与5 个等级范例的正切相似度，得到5 个度量值Tk（Ⅰ，S）、Tk（Ⅱ，S）、Tk（Ⅲ，S）、Tk（Ⅳ，S）、Tk（V，S）。

计算得到的5 个度量值中的最大度量值所对应范例的等级就是该样本的计算等级。例如max（Tk）=Tk（Ⅰ，S），代表该隧道样本的风险计算等级为Ⅰ（极低风险）。

3 工程应用

3.1 工程背景

杨家山隧道位于浙江省内，是杭金衢高速至杭绍台高速联络线的重点工程项目，也是浙江省内第一座双向八车道特大断面隧道。隧道左线全长320 m，右线全长325 m，位于低山丘陵区，属于山岭隧道。杨家山隧道的工程特点是断面面积大、穿越围岩软弱、埋深较浅。

3.2 评估过程

通过查阅杨家山隧道工程设计资料信息，选取杨家山隧道中最不利断面，得到杨家山隧道风险指标参数见表5。

表5 杨家山隧道风险指标参数

将表5 中的数据归一化，并根据中智数原理表达为中智数的形式，设定不确定值Y∈[0，0.25]，得到中智数形式下的杨家山隧道风险指标参数见表6。

表6 中智数形式下的杨家山隧道风险指标参数

采用层次分析法、熵权法计算得到杨家山隧道影响因素的综合权重值向量A=（0.202，0.160，0.167，0.162，0.045，0.062，0.072，0.147，0.142，0.140），将其代入公式（3），计算杨家山隧道样本S 与5 个等级范例的正切相似度，得到Tk（Ⅰ，S）=0.367、Tk（Ⅱ，S）=0.602、Tk（Ⅲ，S）=0.787、Tk（Ⅳ，S）=0.705、Tk（V，S）=0.685。从计算结果可知：Tk（Ⅲ，S）＞Tk（Ⅳ，S）＞Tk（Ⅴ，S）＞Tk（Ⅱ，S）＞Tk（I，S），则max（Tk）=Tk（Ⅲ，S）。因此，杨家山隧道的的计算风险水平为Ⅲ（一般风险）。

4 结论

该文基于中智理论，综合考虑了隧道风险因素中的不确定信息，采用中智数正切相似度量法对杨家山大断面隧道进行风险评估，得到以下3 个结论：1）该文以浙江省杨家山隧道项目为例，详细列举了采用中智理论对大断面隧道进行风险评价的流程，并得出杨家山隧道项目的风险为一般风险的结论。2）综合考虑隧道风险因素中不确定的信息，采用中智数建立中智数形式下的隧道风险因素评价表，提高隧道风险评估的准确性。3）将中智理论应用于隧道的风险评估中，为同类大断面隧道的风险评估提供借鉴。