泥浆发电机用磁力传动机构的转矩影响因素分析

闫文辉,袁亨通,李 杰,彭 勇,邵 军

(1.西安石油大学 机械工程学院,陕西 西安 710065;2.西部金属材料股份有限公司,陕西 西安 710201;3.中国石油集团渤海钻探工程有限公司,天津 300457)

引 言

磁力传动是一种非接触式的动力传递方式,采用磁力耦合作用实现。与传统的刚性连接不同,磁力传动利用磁场透过磁路工作气隙和隔离套传递扭矩,能从根本上解决工程上的泄漏问题,具有零泄漏、容错性强的密封特点,在磁力泵[1-2]、联轴器[3]、抽油机[4]、井下电机[5-6]以及搅拌设备[7]中应用广泛。

磁力传动机构设计的关键是磁路结构设计和磁转矩的准确计算[8-10]。磁转矩的计算方法多且复杂,工程上常用的两种理论方法是静磁能扭矩求解法和气隙数值求导法[11]。在设计过程中,磁力传动机构的磁路结构和各项参数对输出的磁转矩的影响较大,因此有必要研究各参数对磁转矩的影响。在此背景下,本文将通过理论方法对泥浆发电机用磁力传动机构进行磁路设计,并建立有限元模型,分析磁场和涡流损耗,绘制各物理参数和磁转矩的关系曲线,最后进行磁力传动性能测试实验,验证理论和仿真结果的准确性。

1 结构原理和理论计算

1.1 基本原理和结构

基于磁力传动机构的补偿式动密封泥浆发电机的基本结构如图1所示。该发电机的工作原理为：泥浆驱动涡轮叶片4旋转,带动磁力驱动外壳7和固定在其内部的外磁转子5旋转,固定在输出轴18上的内磁转子6和外磁转子5构成磁力耦合传动,会跟随外磁转子6同步旋转,输出轴18带动发电机永磁体13旋转,形成的旋转磁场被发电机电子线圈12切割产生电流,电流经过电子仓16整流稳压后供给井下随钻测量仪器。补偿弹簧2和9、活塞环2和13以及动密封组件3和8组成两对补偿式动密封,内部充满高温润滑油,补偿弹簧提供一定压力保证内部润滑油压力大于外部,防止泥浆进入动密封,提高了整体的密封性能。

注：1-隔离套;2-补偿弹簧;3-活塞环;4-涡轮叶片;5-外磁转子;6-内磁转子;7-磁力驱动外壳;8-活塞环;9-补偿弹簧;10-接头;11-轴承座;12-发电机电子线圈;13-发电机永磁体;14-轴承座;15-发电机外壳;16-电子仓;17-角接触球轴承;18-输出轴;19-定位环;20-角接触球轴承;21-高速推力轴承;22-高速扶正轴承;23-高速扶正轴承;24-深沟球轴承;25-螺栓;26-垫片;27-端盖图1 磁力传动泥浆发电机结构示意图Fig.1 Structure diagram of magnetic drive mud generator

1.2 理论计算

目前国内工程上磁转矩常用高斯定理求解,其最大磁力矩的简化计算公式如下[12]：

(1)

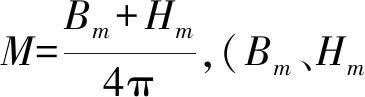
根据上述公式选取相应参数,磁路系数K取6.4,经验系数N1取1.24,磁极厚度系数η取0.7,推导获得圆筒式磁力传动机构内外磁转子的永磁体长度

(2)

1.3 设计要求及计算结果

该泥浆发电机用磁力传动机构设计要求的已知参数包括额定功率1 300 W,额定转速1 000 r/min,因此所需最大转矩需满足12.5 N·m。根据设计要求,计算所需已知参数见表1。

表1 磁力传动机构永磁体长度计算的已知参数Tab.1 Known parameters for length calculation of permanent magnet of magnetic drive mechanism

结合上述公式计算所需钐钴永磁体的长度L,得到理论计算结果为23.2 cm,考虑到摩擦和漏磁等因素影响,取L=25.0 cm,在磁力矩的公式中进行核验,得到理论结果为13.48 N·m,满足设计要求。

2 磁场仿真分析

利用上述参数在ANSYS Maxwell中建立磁力传动机构的二维和三维简化模型,如图2所示。从内到外分别为内基体、内永磁体、隔离套、外永磁体和外基体,基体层材料为硅钢,隔离套为钛合金,永磁体为钐钴,其余部分为空气。空气最外层设置无限边界条件,内基体内侧和外基体外侧由软件自动加载自然边界条件。采用四面体网格划分,对二维模型进行静态和瞬态磁场仿真,对三维模型进行静态磁场仿真。

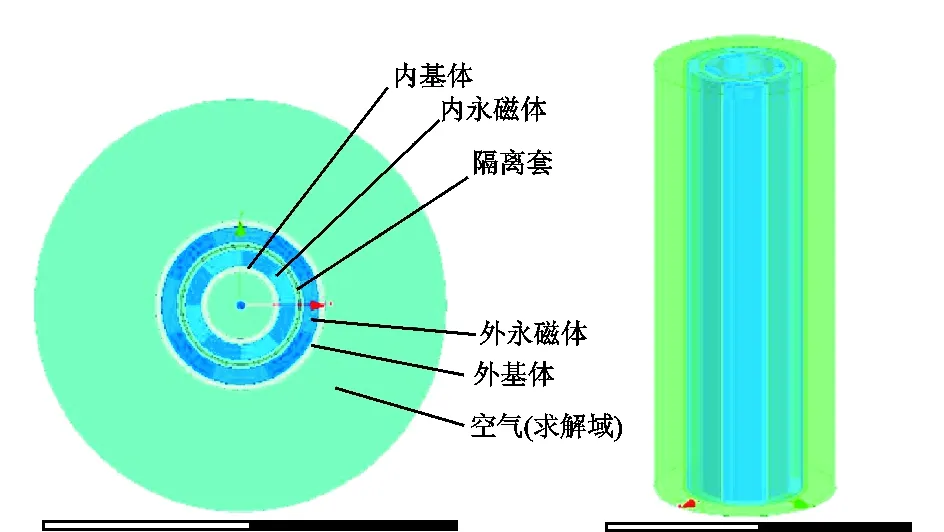
图2 磁力传动机构有限元仿真模型Fig.2 Finite element simulation model of magnetic drive mechanism

2.1 二维静态磁场仿真

磁力传动机构静止时,模型整体的磁通密度分布如图3所示。内外基体材料为硅钢,导磁性好,磁场能轻易通过基体形成回路,两个永磁体交界处的基体上的磁通密度最大,最大值可达到2.850 4 T。

内磁转子外径处磁通密度沿周向分布曲线如图4所示。可以发现,磁通密度沿内磁转子外径圆周方向呈周期性分布且周期数与永磁体数目相同,说明磁力传动机构内的总磁场是由所有永磁体产生的磁场叠加形成的。

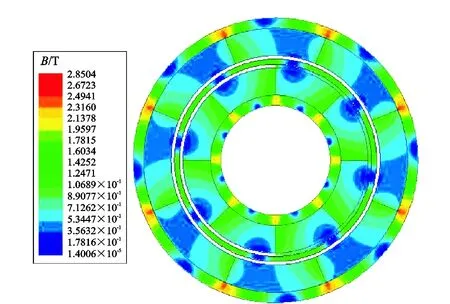
图3 磁力传动机构二维模型磁通密度分布图Fig.3 Magnetic flux density distribution of 2D model of magnetic drive mechanism

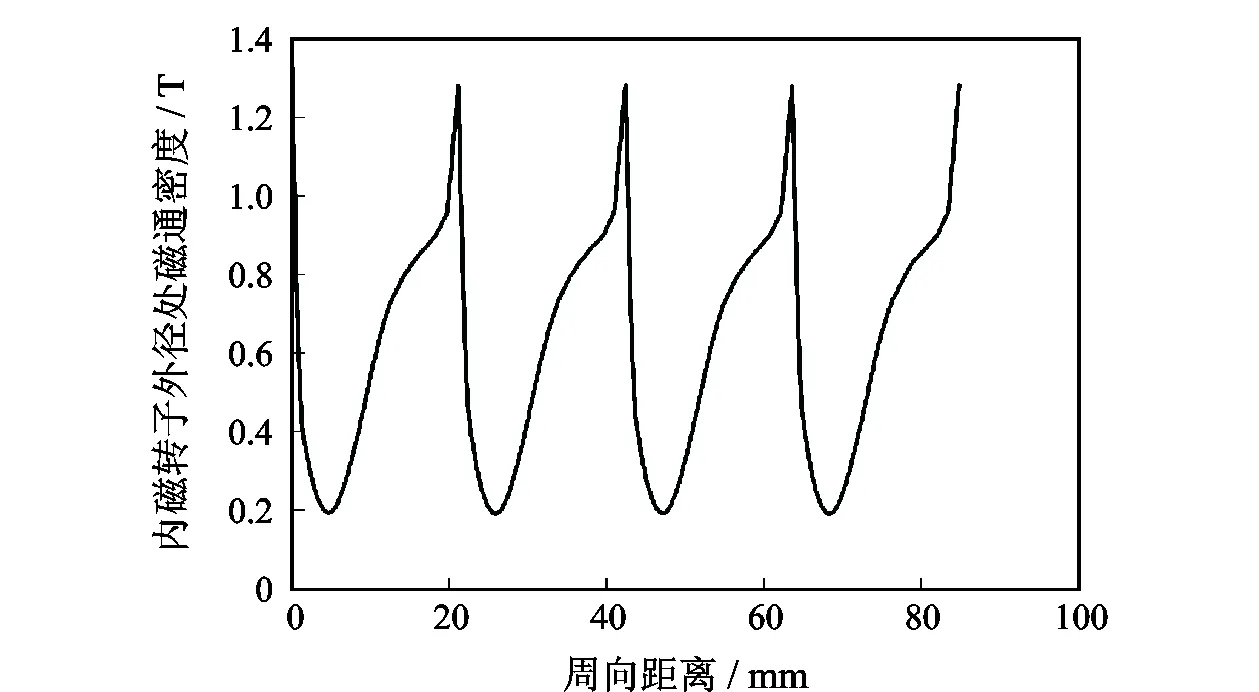
图4 内磁转子外径处磁通密度沿周向分布曲线Fig.4 Circumferential distribution curve of magnetic flux density at outer diameter of inner magnetic rotor

2.2 二维瞬态磁场分析

实际工作中隔离套固定不动,内外磁转子同步转动,在瞬态磁场仿真中令内外磁转子静止,给隔离套创建一个转速为1 000 r/min的band运动区域,由于法拉第电磁感应原理,隔离套将产生涡流效应。涡流效应产生的欧姆损耗在隔离套上的密度分布如图5所示。由图5可知,在内外永磁体磁极互异处,即磁力线穿过处产生的欧姆损耗密度最大,为3.943 8×106W/m3。

2.3 三维静态磁场

在二维模型中忽略了端部效应和磁场轴向分布对磁力传动机构磁场的影响,因此需要在三维模型中进行分析。磁力传动机构三维模型磁通密度分布如图6所示。由图6可知,最大磁通密度为2.288 0 T,对比二维模型的最大磁通密度减少了19.7%,这是由于在二维分析中忽略了内外磁转子轴向的漏磁,因此在端盖材料选择时,应选择对磁场密封较好的软磁材料。

图5 隔离套欧姆损耗密度分布Fig.5 Ohmic loss density distribution of insulator

图6 磁力传动机构三维模型磁通密度分布图Fig.6 Magnetic flux density distribution of 3D model of magnetic drive mechanism

在仿真结果中获得最大磁力矩的仿真值为14.53 N·m,对比理论值,相对误差约为7.8 %,分析误差产生的原因：(1)磁力矩计算公式需要选择经验系数,公式本身存在约10 %的误差;(2)Maxwell软件的网格划分,求解方法产生的误差。

3 影响因素分析

3.1 相对磁轴偏角对磁转矩的影响

基于上述模型的基本参数,模拟永磁体相对磁轴偏角对磁转矩的影响。根据仿真结果,绘制不同磁极数目对应模型的相对磁偏角与磁转矩的关系曲线如图7所示。由图7可知磁转矩呈正弦周期性变化,变化周期为4π/m(m为磁极数目),在一个周期内,磁转矩在π/m时达到最大磁转矩,即临界值。正常工作时,磁转矩对应的磁轴偏角维持在0～π/m之间,超过这个范围将发生过载滑脱,引起机械振动和噪声。

图7 不同极数下相对磁轴偏角与磁转矩的关系Fig.7 Relationship between relative magnetic declination and magnetic torque under different pole numbers

3.2 磁极数目对传动性能的影响

将磁极数目(分别取4、6、8、10、12极)作为变量,保持其他参数不变,仿真得到的最大磁转矩和涡流损耗与磁极数目的关系曲线如图8所示。由图8可知,最大磁转矩和涡流损耗随磁极数目的增加都具有先增加再逐渐减小的趋势,最大磁转矩在磁极数目为8～10之间时达到最大值,涡流损耗在磁极数目为6～8之间时达到最大值。这是因为在磁力传动过程中,内外磁极之间的每一次排斥和吸引,都是静磁能的储存过程,所储存的静磁能随着磁极数目的增加而增加,从而增大磁转矩的值。但是,磁极数目不能连续增加,当磁极数目过多时,不同永磁体之间的非必要磁极接触会导致部分磁力的浪费,增加的磁通密度不足以抵消增加的漏磁,气隙中总的磁通密度降低,影响磁转矩传递,降低磁力传动的效率[13]。此外,增加磁极数目将增加生产零件的数量,从而增加生产成本和装配难度。综上所述,磁力传动模型中的磁极数目设定为8是最优的。

图8 最大磁转矩和涡流损耗与磁极数目的关系Fig.8 Relationships between maximum magnetic torque,eddy current loss and number of magnetic poles

3.3 永磁体厚度对最大磁转矩的影响

将永磁体厚度(分别取0.5、1、2、4、6、8、10 mm)作为变量,保持其他参数不变,仿真得到不同磁极数目下永磁体厚度和最大磁转矩的关系曲线如图9所示。由图9可知,最大磁转矩随着永磁体厚度的增加而增大,但增长率逐渐减小,而且随着磁极数目的增加,这种减小的趋势更加明显。分析可知,永磁体厚度的增加会加大单个磁极的磁势,从而提高工作气隙中的磁通密度,但同时磁阻和漏磁占总磁势的比例也随着永磁体厚度的增加而增大,漏磁会随着磁极数目的增加而增大,从而导致最大磁转矩的增长率逐渐减小,而且磁极数目越多,减小的趋势越明显。根据曲线趋势可以推测,当永磁体厚度达到对应的某一值时,最大磁转矩的增长率为0,此时对应最大磁转矩的最大值。考虑到永磁体厚度的增加会加大永磁材料的消耗,因此在实际应用过程中需要考虑单位体积增加的磁转矩与价格的比例关系,从而选择合适的永磁体厚度。

图9 不同极数下永磁体厚度与最大磁转矩的关系Fig.9 Relationships between thickness of permanent magnet and maximum magnetic torque under different pole numbers

3.4 基体层相对磁导率对最大磁转矩的影响

将基体层相对磁导率(分别取1、1.5、2、2.5、3、3.5、4)和磁极数目(分别取4、6、8、10、12极)作为变量,保持其他参数不变,仿真得到基体相对磁导率和磁极数目与最大磁转矩的关系如图10所示。从图10可知,当磁极数目一定时,基体层相对磁导率对最大磁转矩的影响是比较大的,这是因为永磁体的磁通可以通过内外基体层形成回路,增大磁路中的磁通密度,同时减小漏磁。基体层的相对磁导率越大,这种性能越好,因此在实际应用时一般选用相对磁导率大、矫顽力小和饱和磁化强度小的材料作为基体层。另外从图中还可以看出,基体相对磁导率一定时,随着磁极数目的增加,最大磁转矩具有先增大后减小的趋势,这与上述分析吻合。

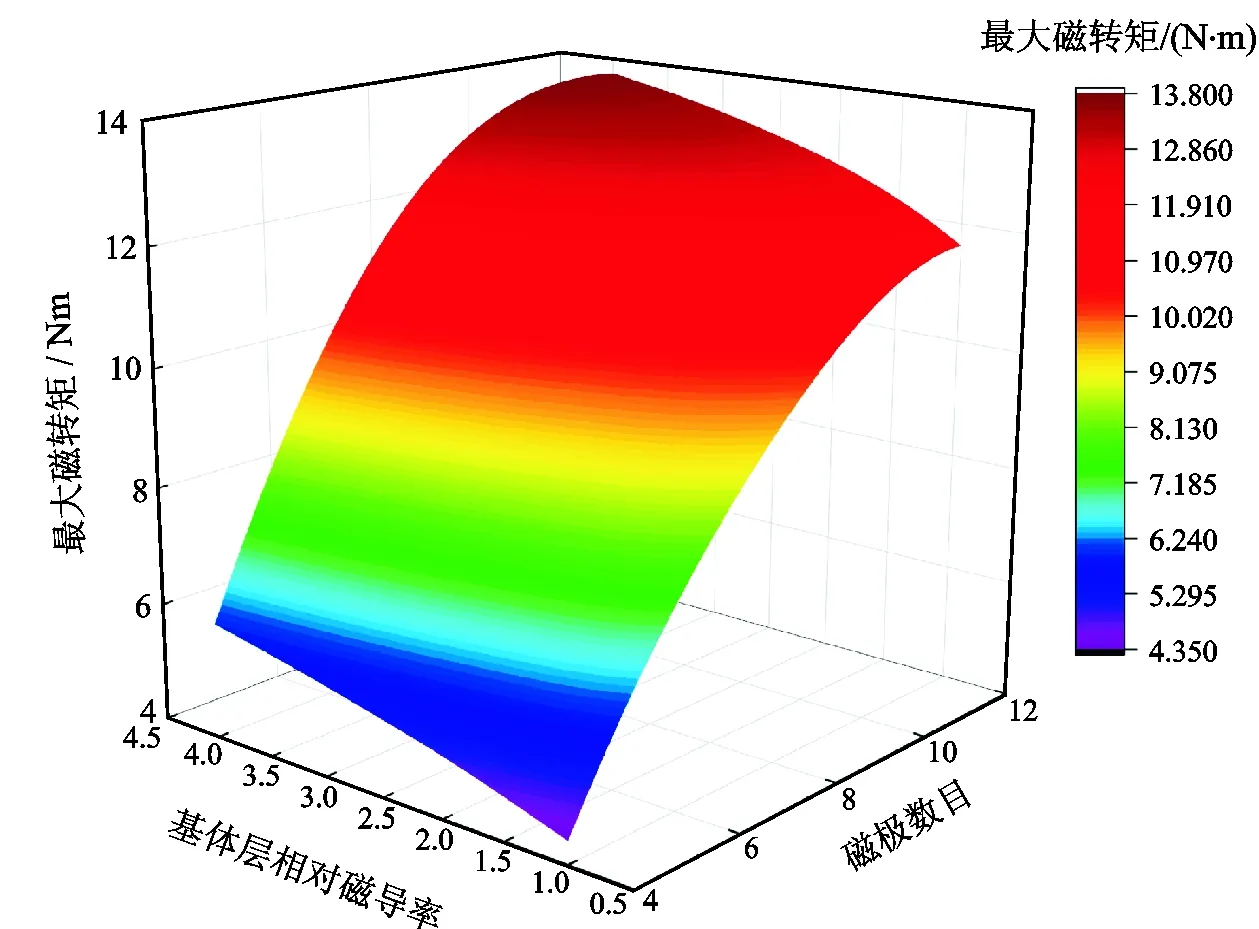
图10 最大磁转矩与磁极数目和基体层相对磁导率的关系Fig.10 Relationship between maximum magnetic torque and magnetic pole number,relative magnetoconductivity of matrix layer

3.5 隔离套厚度对传动性能的影响

将隔离套厚度(分别取1.1、1.3、1.5、1.7、1.9 mm)作为变量,保持其他参数不变,仿真得到最大磁转矩和涡流损耗与隔离套厚度的关系曲线如图11所示。从图11可知,最大磁转矩和涡流损耗与隔离套厚度基本都呈线性关系,随着隔离套厚度的增加,对磁路中磁通的屏蔽增大,消耗在隔离套上的涡流损耗逐渐增大,同时减小了工作气隙中的磁通密度,最大磁转矩也逐渐减小。

隔离套具有隔离和密封的作用,处在运动的磁场中会产生涡流,从而引起发热,同时需承受外部压力,因此选材需要满足4个基本要求：机械性能优秀、化学性能稳定、导磁性低和电阻高。隔离套的材料分为金属和非金属,非金属材料一般选择塑料和陶瓷,金属材料有奥氏体不锈钢、哈氏合金以及钛合金[14]。

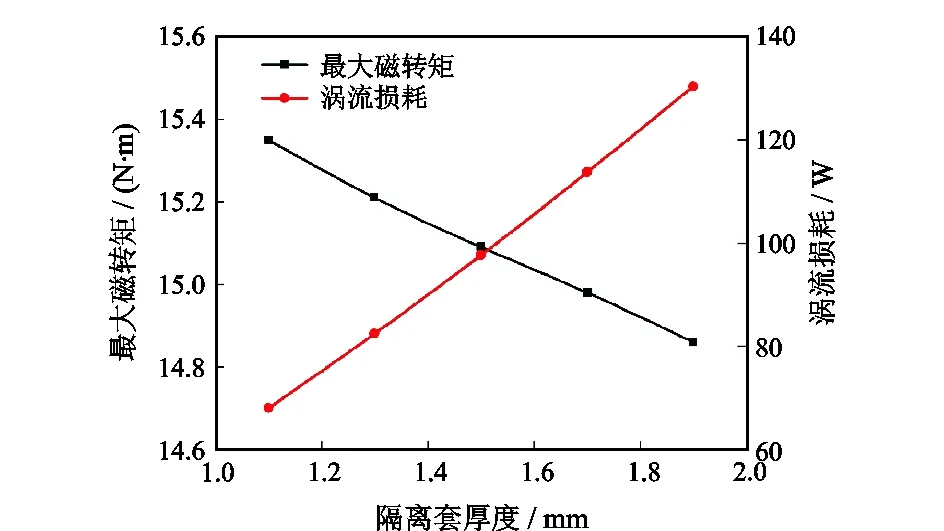
图11 最大磁转矩和涡流损耗与隔离套厚度的关系Fig.11 Relationships between maximum magnetic torque,eddy current loss and the thickness of isolation sleeve

3.6 工作气隙厚度对传动性能的影响

将工作气隙厚度(分别取2、2.5、3、3.5、4 mm)作为变量,保持其他参数不变,仿真得到最大磁转矩和涡流损耗与工作气隙厚度的关系如图12所示。由图12可知,随着工作气隙厚度的增加,涡流损耗和最大磁转矩值都逐渐减小。这是因为工作气隙的磁阻远远大于永磁体的磁阻,永磁体消耗在工作气隙中的磁通密度随工作气隙厚度的增大而增大,能穿过隔离套的磁通密度减少,隔离套上产生的涡流损耗也就越少,最大磁转矩也会减小。因此在保证制造和安装方便的前提下,尽量将工作气隙厚度设计得越小越好。

图12 最大磁转矩和涡流损耗与工作气隙厚度的关系Fig.12 Relationships between maximum magnetic torque,eddy current loss and working air gap thickness

3.7 转速对涡流损耗的影响

磁感应强度和磁转矩的大小与转速无关,但涡流损耗的大小与转速相关。将转速(分别取500、700、900、1 100、1 300、1 500 r/min)作为变量,保持其他参数不变,仿真得到涡流损耗与转速的关系如图13所示。从图13可知,涡流损耗随转速的增大而增大,这是因为转速的增加会增大感应电流的频率,从而增大涡流损耗。涡流损耗会产生热量,增加能耗,降低工作效率,产生的热量若不及时散出还会使永磁体退磁,甚至导致整个传动机构无法工作,因此在设计时需要考虑到涡流损耗的影响[15-16]。

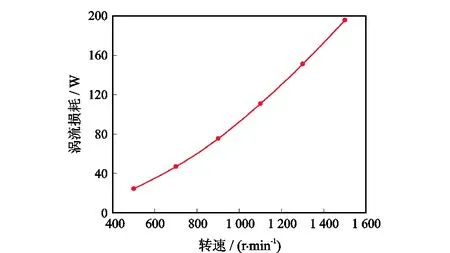
图13 涡流损耗与转速的关系Fig.13 Relationship between eddy current loss and rotating speed

4 实验分析

为了进一步验证理论计算和仿真分析的准确性,构建了磁力传动性能测试实验台[17]。实验台包括变频电机、联轴器、扭矩仪、轴承座、传感器、磁粉制动器和主控制面板等,实验台如图14所示,可以测试输入输出扭矩、内外磁转子间的温度和磁场情况、发电机的输出功率等性能测试工作。

图14 磁力传动性能测试实验台Fig.14 Magnetic transmission system performance test bench

选择4组结构参数不同的试件进行实验,获得不同结构参数试件的实验数据与理论仿真结果比较见表2。从表2可以看出,4组结构参数不同的试件的理论、仿真和实验值基本一致,相较于理论值的误差基本控制在15%以内,从而验证了高斯定理和有限元仿真方法是比较准确的,可以用来作为设计磁力传动机构的依据。

表2 不同结构参数试件的实验数据与理论仿真结果比较Tab.2 Comparison of experimental,theoretical and simulation results of maximum magnetic torque of specimens with different structural parameters

5 结 论

(1)磁通密度最大值在永磁体交界处的基体层;磁通密度沿内磁转子外径圆周方向呈周期性分布且周期数与永磁体个数相同;端部效应会产生漏磁从而减小磁通密度。

(2)磁转矩与相对磁轴偏角呈正弦周期性变化;最大磁转矩和涡流损耗都随磁极数目的增加先增加后减小,磁极数目选择8对,磁转矩最大;最大磁转矩随磁极厚度的增大而增大,但增长率逐渐减小;最大磁转矩随基体层相对磁导率的增大而增大。

(3)随着隔离套厚度的增加,最大磁转矩逐渐减小,涡流损耗逐渐增大;最大磁转矩和涡流损耗都随工作气隙厚度的增加而减小;涡流损耗随转速的增大而增大。

(4)高斯定理计算磁转矩和Maxwell磁场仿真可作为基础的设计方法应用在泥浆发电机用磁力传动机构的设计过程中。