井下指令信号的小波-奇异值分解双层滤波降噪

霍爱清,王泽文,胥静蓉,张书涵

(西安石油大学 电子工程学院,陕西 西安 710065)

引 言

为了更好地实现旋转导向钻井系统中控制指令向井下的传输,需要采用改变钻井液排量的方法。该方法通过下行通道传输“三降三升”脉宽编码控制指令[1]。凭借井下信号接收设备实现对电机电压的采集与检测,以此获取与之对应的钻井液排量,然后结合下传指令信号变化的脉冲沿产生的时间和顺序,根据对5个指令码脉冲宽度的解析,最终获得精准的下传控制命令字[2]。但下传指令信号的传输会因环境因素受到干扰而产生噪声,因此对井下接收的指令信号进行降噪处理成为获取控制指令的关键技术。

小波变换以频率和多尺度分解来描述非平稳信号,因其计算复杂度低,广泛应用于非平稳信号的降噪[3-4]。从Donoho的小波阈值降噪法[5]可知,即便是对小波变换过程中全局阈值的最优值进行降噪处理,其结果的延时和震荡也是不可避免的[6]。由于阈值函数对信号最终的检测影响极大,所以,如何选取合适的阈值函数对于信号重建和检测的效果起着至关重要的作用。此外,一般情况下常用的硬阈值、软阈值函数都存在着不连续、易偏差等问题,这也使得信号经过重构后会发生局部震荡,并且容易造成提取信号的细节丢失[7]。多数研究指出阈值和阈值函数的不同对降噪效果影响极大[8-9]。传统的小波阈值去噪法所提出的阈值函数存在着不连续、重构信号存在第二类间断点、软阈值函数存在恒定偏差等问题[10]。为此,有学者提出了一种可以基本消除噪声的方法,即改进分层阈值降噪法,但此方法依旧无法改变下传信号出现奇异点和突变点的情况,而这些奇异点和突变点将对脉宽信号的识别带来严重影响[11]。为应对这类问题和情况,本文提出了一种基于奇异值分解的双层滤波降噪法,通过小波降噪与奇异值分解降噪两种方法的结合,实现了对下传信号的双层滤波处理。

1 WT-SVD双层滤波降噪方法

小波变换与奇异值分解(Wavelet Transform-Singular Value Decomposition,WT-SVD)双层滤波降噪是基于奇异值分解法的小波降噪方法,为满足对信号的降噪需求,采用了小波变换降噪与奇异值分解降噪相结合的双重降噪法。其主要步骤分为两步,第一步先对下传信号进行小波降噪,第二步通过奇异值分解法再对其进行进一步的降噪处理。

1.1 小波分层阈值降噪

分层阈值降噪法相较于全局阈值,是基于各层小波系数的自相关性确定各层合适的阈值降噪,不会严重“扼杀”小波系数和有用信号的高频部分,能够保证信号的真实完整性[12]。因此,为了解决硬阈值的不连续、软阈值的恒定偏差、全局阈值的延时和震荡以及不同尺度噪声在经历小波分解后导致系数上存在差异的问题,本文在第一层滤波降噪环节采用改进分层阈值降噪方法,以此来使得阈值作用过渡平滑[13]。改进的阈值函数如下：

(1)

该表达式分为以下两种情况,其一是小波系数的绝对值相较于临界阈值更小时,以0作为其对应系数,该情况下会使得其变成常规阈值函数;与之相反,当小波系数的绝对值相较于临界阈值较大时,则通过表达式对其进行对应的收缩。图1为软、硬阈值函数和改进阈值函数的比较。

改进阈值函数在软、硬阈值函数之间,并且在小波域中具有连续性和灵活性,避免了硬阈值函数的不稳定性和软阈值函数的易偏差性等问题[14-15]。

1.2 奇异值分解降噪

奇异值分解(SVD)被认为是数值代数中最强大的工具之一,并且在各种数据处理任务中取得了巨大的成功[16]。作为一种正交变换,奇异值分解(SVD)实现了从原始矩阵到对角阵的变换,其特征值反映了矩阵的一些主要特征。作为一种数据处理方法,SVD已成功应用于信号去噪,并被证明可以有效避免模态混叠[17]。奇异值分解降噪法的核心思想是将信号的信息分量与重构矩阵的奇异值关联起来,通过奇异值的大小反映信息分量的大小[18]。奇异值分解在处理信号数据的过程中,主要体现出的是将奇异值大的矩阵信号进行保留,同时去除奇异值小的矩阵信号,那么如何合理地将小奇异值的信号分量去除,并且用大的奇异值来复原原始信号就变得尤为重要。SVD在保证对噪声抗干扰能力的同时,能最大程度地保存原始信号的主要特征信息,而且还能减小信号的损失,大大提高信号在被分解处理后的真实性,最终更准确地获得降噪后的信号[19]。

图1 软、硬阈值函数和改进阈值函数的对比Fig.1 Comparison among soft and hard threshold and improved threshold functions

奇异值分解降噪法的基本步骤为：

(1)利用下传指令信号S=(s(1),s(2),s(3),…,s(N))构造矩阵E;

(2)对矩阵E进行奇异值分解,得到U=Rm×m,Σ∈Rm×n及V∈Rn×n,则E=U·Σ·VT;

(3)为奇异值矩阵Σ选择更大的奇异值进行处理,得到处理后的矩阵Σ*;

(4)利用矩阵U=Rm×m、V∈Rn×n及Σ*重构矩阵,得E*=U·Σ*·VT;

(5)由矩阵E*第1行的所有元素和第2行第n列至第m行第n列的元素,构造新的数据序列S*,即为降噪后的信号。

在改进分层阈值的小波降噪法单独作用的情况下可以有效减少噪声,但依旧不能将信号中存在的奇异点和突变点消除。为此,本文将改进分层阈值降噪与奇异值分解降噪两种方法相结合,进行双层滤波降噪处理,以达到更好的降噪效果。

2 双层滤波降噪的关键点

将双层滤波降噪应用于信号处理来降低信号噪声的关键环节主要包括3个方面：利用信号序列构造出合适的矩阵,选择非零奇异值的数量,以及确定重构矩阵的结构。

2.1 重构矩阵方法的选择

重构矩阵的方法主要包括连续截断法和Hankel矩阵法。

(1)连续截断法

对一维信号,每次在连续n个点处被m个段进行截取,以构建如下矩阵：

(2)

式中：A∈Rm×n,m×n=N,s(k) (k=1,2,…,N)为一维信号序列。

(2)Hankel矩阵法

Hankel矩阵[20]也称重构吸引子矩阵,它可利用信号S=(s(1),s(2),s(3),…,s(N))构造如下矩阵：

(3)

相对于连续截断法在矩阵行数选取上的限制,Hankel矩阵法在行数的选取上则有着更多的优势,它不仅可以调节构造矩阵的行数,而且行数的选取是任意的,可以取为L=2,…,N-1,使其在设计上更为灵活和自由。虽然连续截断法在信号降噪过程中频率分辨能力很突出,但Hankel矩阵法降噪能力更好。为此本文选取Hankel矩阵法对信号序列进行重构。

2.2 奇异值数量的选择

奇异值分解法凭借其突出的降噪优势成为了大多数情况下的降噪选择,但能否选取合适的奇异值个数才是其最为关键的问题。倘若选取的个数较多,信号的降噪效果将大幅度下降;如果选取的个数较少,则会造成信号失真[21]。所以本文采用不同的方法进行奇异值数量的选择,比如：①特征均值法;②差分谱法;③奇异值中值法。在经过大量的数据计算后可以知道：当L≤n时,p=L;当L>n时,恒有p=2n。

2.3 重构矩阵结构的确定

选取矩阵行数时,经常会根据信号所对应的情况试凑,即通过不断地对每组矩阵的特征进行分析实验,来尝试获取较好的结果,但由于该方法计算量极大,所以对于实验研究人员的要求极高。

对于下传指令信号构造出的矩阵E进行奇异值分解,得到U=Rm×m,Σ∈Rm×n及V∈Rn×n,则E=U·Σ·VT,其中分离得到各个信号分量Σi=diag(σ1,σ2,…,σi),其中奇异值的大小则反映了所包含信息量δi的多少,奇异值σi越大,其Σi的信息量则越大。对应Σi包含的信息量δi可以通过

(4)

计算得到。

由于信息量较小的信号分量对于结果来说并无影响,故采用以下步骤选择对应矩阵的行数和列数。

Step1：对不同行数m分别进行矩阵构造。

Step2：根据其奇异值求出对应的信息量分量,在经过观测和分析后找出其中对应的联系与变化。若某一分量δi后的其余分量开始趋近于零,则第i个分量后的部分对结果几乎没有影响,由此可以根据这一规律确定矩阵的行数m=i。这种只通过奇异值所包含信息来完成判断的方法大大降低了计算量。

Step3：对于列数的计算,连续截断法为n=int(N/m),Hankel矩阵法为n=N-m+1。

3 实验与结果分析

3.1 奇异值数量与重构矩阵结构的确定

3.1.1 奇异值数量的确定

图2所示为井下所接收到的指令信号(对应512个采样点),即N=512。通过快速傅立叶变换,可以得到图3所示的信号频谱图,该图谱主要反映了其对应的主频率数量以及分布情况,通过该频谱图中的箭头位置,可以获得该信号主频的个数n=9。

本文采取奇异值分解的最主要原因不仅是因为其可以去噪,同时还可以兼顾数据简化这一功能。通过分析下传信号奇异值分解后的结果可以发现,奇异值由大到小地进行高速率的衰减,对式(4)进行分析计算可知,前10%的奇异值之和已经达到了其总体的95%以上,足以囊括信号中所包含的所有信息,因此奇异值个数不需取得很大。

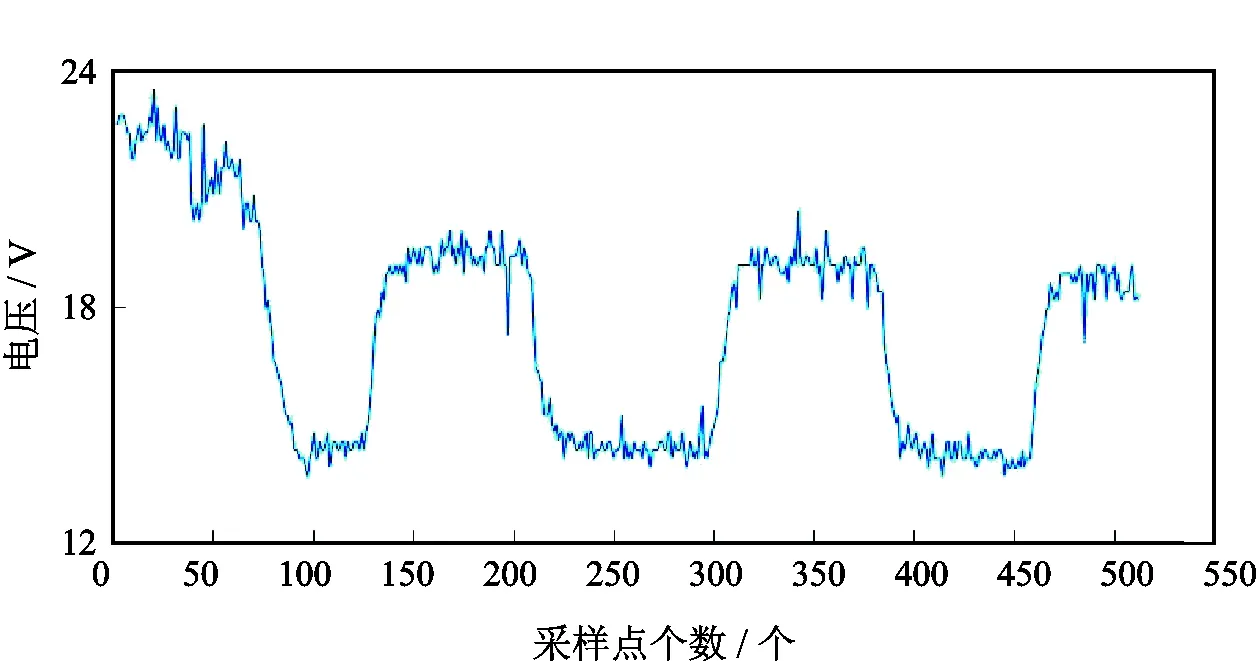
图2 井下接收的下传信号Fig.2 Downgoing signal received in the well

图3 信号的频谱图Fig.3 Signal spectrogram

对奇异值分解(SVD)和小波结合奇异值分解(WT-SVD)两种降噪方法进行实验,选取不同的奇异值,获得其相应的信噪比(Signal-Noise Ratio,SNR)曲线如图4所示。

图4 重构矩阵取不同奇异值时的信噪比曲线Fig.4 Signal-to-noise ratio curves under different singular values of reconstruction matrix

由图4可见,随着奇异值个数的增多,信噪比会相应上升,而当奇异值个数超过18,上升趋势则会变得平缓。

为了更好地获取降噪效果,选取了10、18、25、40这4个具有代表性的奇异值个数值进行了指令信号的降噪WT-SVD实验,实验结果如图5所示。通过图5中的对应波形可见：当奇异值的个数c=18时的波形效果最好,可以完全满足去除奇异点的需求。

综合图4和图5的信息可知,针对图2所示的井下指令信号c=18为选取的最优奇异值个数,当指令信号不同时,可以采用相同的方法进行奇异值个数选取。

3.1.2 重构矩阵结构的确定

在确定重构矩阵的结构时,选取合适的重构矩阵行数至关重要。已知实验的下传指令信号的采样点N=512,当选取的行数L=2,3,…,255等值时,无法取得靠后信号的采样点信息,而产生信息丢失。当选取的行数L=257,258,…,511等值时,则会由于缺少2L-512个采样点,导致重复获取信息,使得最终结果信息冗杂。经大量实验后可确定当选取的行数L=256,即采样点数一半时,可满足所需的降噪效果。

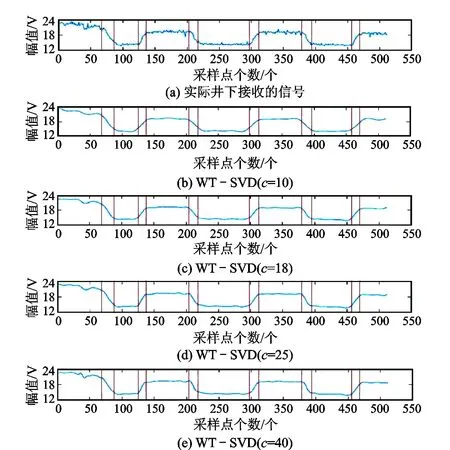
图5 重构矩阵取不同奇异值数量降噪后的信号波形Fig.5 Signal waveforms after noise reduction under different singular values of reconstruction matrix

3.2 多种降噪方法对比实验

分别采用奇异值分解(SVD)法、Sym6小波改进分层阈值(WT)法和WT-SVD双层降噪法进行下传指令降噪实验,降噪效果如图6所示。

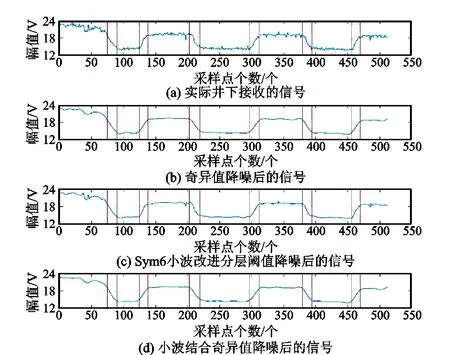
图6 3种不同降噪方法降噪后的信号波形Fig.6 Signal waveforms after noise reduction with 3 noise reduction methods

由图6可知,未经降噪处理的信号受噪声影响较大,将原始信号单独经过奇异值分解(SVD)和Sym6小波改进分层阈值(WT)后降噪效果并不理想,而将这两种方法相结合后,信号波形变得更为平滑且失真较小,可以满足对原始指令信号的降噪需求。

表1为采用SVD、WT及WT-SVD这3种不同降噪方法获得的信噪比、均方根误差RMSE(Root of Mean Square Error)和相关系数ρ的数据对比。

表1 不同降噪方法降噪后的SNR、RMSE和ρ对比Tab.1 Comparison of SNR,RMSE and ρ values after noise reduction using different noise reduction methods

由表1可见,WT-SVD双层滤波降噪后SNR为37.710 9,RMSE为0.164 3,相关系数为0.996 4,与SVD和Sym6小波改进分层阈值(WT)降噪数据相比都有所提高,说明WT-SVD双层滤波降噪方法对井下指令信号有着更优的降噪效果,WT-SVD双层滤波降噪后的信号更有利于三降和三升脉冲宽度的准确识别。

4 结 语

本文提出了一种基于小波的奇异值分解双层滤波降噪方法(WT-SVD),该方法将小波改进分层阈值降噪与奇异值分解降噪相结合。在对井下的下传指令信号进行改进分层阈值降噪后,采用Hankel矩阵法构造矩阵,在确定出奇异值个数与重构矩阵结构后,对该矩阵进行奇异值分解与重构恢复信号。实验将WT-SVD双层滤波降噪方法与其他方法进行对比,验证了该方法能够有效去除噪声中的奇异点和突变点,具有更优的降噪效果,为进一步井下接收指令信号的编码识别提供了保证。