基于改进层次分析法的无人机作战效能评估方法研究*
2023-06-05寇昆湖刘登攀鹿珂珂
寇昆湖 刘登攀 钱 峰 鹿珂珂
(海军航空大学 烟台 264001)
1 引言
无人机作为一种新质作战力量已在侦察、电子对抗、通信中继等领域发挥了重要作用,成为我军战斗力新的增长点,科学评估无人机的作战效能对于提升体系作战能力具有重要意义[1]。以无人侦察机为例,其作战效能主要由无人机的可靠性、生存力、侦察能力等决定[2]。
现阶段关于武器装备的效能评估方法主要有[3~7]:灰色评估法、综合指数模型、模糊综合评判法、ADC法等。
相比较于其他方法,层次分析法具有高度的逻辑性、系统性和实用性,灵活简便。但是使用层次分析法的过程中,主观性较强,其定性分析存在一定的偶然因素。
目前主要是通过定性分析[8~12]来评估无人机的作战效能,在无人机的作战效能与影响因素之间没有一个准确的定量关系,无法精准地提升作战效能。因此,本文在传统层次分析法的基础上,提出改进型的无人侦察机作战效能模型,为以后建立无人机的作战效能与影响因素之间的有效映射提供理论依据。
2 无人机作战效能评估指标体系构建
根据无人机结构、作战影响因素以及演训数据等建立无人机作战效能的指标体系。
2.1 影响无人侦察机作战的主要因素
2.1.1 可靠性能
1)可维护度。无人侦察机可维护度是指无人机系统发生故障时能够排除或抑制故障予以修复,并返回到正常状态执行任务的可能性。可维护度的优劣直接影响到无人机的可靠性能。
2)可靠度。飞机可靠度是指无人侦察机在执行任务期间不发生故障完成任务的概率。该指标与无人侦察机平均故障间隔时间(MTBF)和任务飞行时间紧密相关。平均故障间隔时间是无人侦察机在规定时间内保持有效功能的一种能力,是相邻两次故障之间的平均工作时间[13]。
P为任务完成概率,即飞机可靠度指标。t为无人机飞行时间。MTBF为平均故障间隔时间,一般采用无人机某一部件(最易故障)的平均故障时间。pys为无人侦察机的易损系数。
3)可用度。该指标是指无人机在特定载荷下的持续飞行时间。与无人机续航时间、燃油存储、载重量等密切相关。
2.1.2 生存性能
1)隐身性。隐身能力对于压制敌早期预警能力,提高侦察能力性能有着非常重要的作用。
无人机本身的隐身性与无人机的几何尺寸、气动布局、红外辐射强度、最大雷达反射截面(RCS)密切相关。
RCS在三维空间中的计算为[14]
σ为RCS,Si是在目标处测量的入射功率密度,Ss是远处测量到的散射功率密度,r是目标和雷达之间的距离。
2)机动性。机动性是无人侦察机的重要战术、技术指标,是指无人机在一定时间内改变飞行速度、高度以及方向的能力。相应地称为速度机动性、高度机动性以及方向机动性。改变所需的时间越短,则表示机动性越好。机动性指标与无人机的自身重量、最小转弯半径、最大爬升率有关。
但传统的爬升率概念已经不足以衡量飞机的爬升能力。这时我们需要引入单位剩余功率(SEP)这一概念[15]。
SEP=(T-f)*V/G(m/s)
T为推力,f为阻力,V为飞行速度,G为重力。
根据综合指数模型,无人侦察机机动性指标可以表示为[12]
wp为稳定盘旋过载,表示无人机在做水平盘旋时的最大加速度,Tg为飞机的最大可用加力推力与飞机正常起飞重量,可以表示无人机的加速性能。Ma为飞行马赫数。
ε为操纵效能系数,取值见文献[16]。
3)抗摧毁能力。无人侦察机在执行侦察任务时,需要面对各种突发情况以及敌方的攻击,良好的抗摧毁能力是应对突发情况以及敌方攻击的重要前提。其中包括抗软摧毁能力和抗硬摧毁能力。
抗硬摧毁能力指的是无人机实体的抗摧毁能力,与无人机的机身结构、材料等有关,也与无人机机动性密切相关;抗软摧毁能力指的是无人机指挥系统、通信系统等抗打击、干扰、屏蔽的能力,与无人机的隐身性能以及电子防御性能等密切相关。
2.1.3 侦察性能
无人侦察机侦察能力与其侦察载荷效能直接相关,根据载荷不同,无人侦察机的侦察能力指标主要包括雷达侦察性能、红外侦察性能、航空照相侦察、电视侦察等。不同的载荷其信息获取能力以及信息传输与处理能力不同。
以无人机搭载雷达侦察为例,其信息获取能力指标可由雷达探测领域范围和雷达识别能力来表征。
雷达探测领域范围为
TC表示雷达的信探测领域范围,Rmax为波束最远传播距离,θ为波束仰角。
雷达识别能力[14]与其分辨率直接相关,良好的分辨率是雷达识别物体的关键。
S表示雷达的分辨率,β表示信号宽度,d表示天线孔径尺度,k是单位距离内的采样次数(k=1,2,3…),ηβ为方位角测量误差加权系数,ηε为比幅测角,Td是目标方向上波束的停留时间,θβ为空间方位角,R0为雷达识别能力的参考距离。
2.2 无人侦察机作战效能评估指标体系
在构建过程中,本文将评估指标体系划分为目标层、准则层和指标层。
为了弱化其准则层的定性色彩,在指标层的确定过程中,选取可直接量化的指标,对于不可直接量化的指标,采用线性数据拟合等方法确定其隶属度函数。如图1所示。

图1 无人侦察机效能评估体系
3 改进层次分析法
3.1 经典层次分析法
经典层次分析法一般步骤为
1)首先根据无人机结构、作战影响因素等建立无人机作战效能评估指标体系。
2)利用专家打分方式,比较指标体系各层之间两两不同指标的相对重要程度。根据1-9 标度力量得到各层指标之间的判断矩阵,并做相应的归一化处理。
3)计算各层之间的最大特征值以及相对权重矩阵,并做一致性检验。
4)得到无人机作战总效能表达式。
3.2 改进层次分析法
从经典的层次分析法步骤可以得出传统的方法具有以下劣势:
1)主观因素较大。利用专家打分方式得到的判断矩阵主观性较大,不同专家在对无人机系统的判断上以及各自专业领域、思维的不同,导致得到的数据与实际数据可能存在偏差。
2)计算较为复杂。通过专家打分的方式要想得到较为准确的结果,需要大量的数据,计算较为复杂。
3)可能出现不一致现象。专家的主观认知若与客观实际存在较大差异,则判断矩阵可能不一致,需要进行多次修正,同样需要大量计算。
针对以上问题,本文提出改进的层次分析法,尽可能地减少计算量,避免出现不一致现象,使实验结果更加贴近客观实际。
1)使用最优矩阵减少计算量。
使用最优传递矩阵对传统的层次分析法的判断矩阵进行改进,设置一个调节器,使得其自动满足一致性要求,简化一致性检验步骤,大大较少计算量。
2)采用模糊评判增加定量分析。
采用模糊综合评判对传统的层次分析法进行改进,可以在定性分析的基础上,对各指标因素进行定量分析决策。
改进后的层次分析法步骤如图2所示。
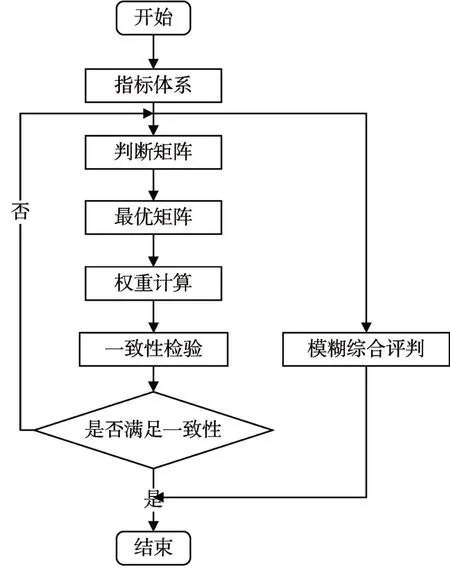
图2 改进层次分析法步骤图
4 基于最优的权重系数矩阵确立
对无人机作战效能评估体系中指标层和准则层的各个元素进行两两比较,构造判断矩阵,确定其对应的权重系数。
以准则层指标重要程度打分结果为例,计算准则层指标的最优判断矩阵[19]。
1)首先给出准则层指标的判断矩阵。
2)计算反对称矩阵J1=lgJ。
3)计算最优传递矩阵。
4)构造判断矩阵拟优一致矩阵。
5)计算相对权重。
至此,得到准则层指标的判断矩阵和相对权重。

表1 准则层等级表
同理,可得指标层可靠性能、生存性能以及侦察性能的相对权重。

表2 可靠性指标等级表
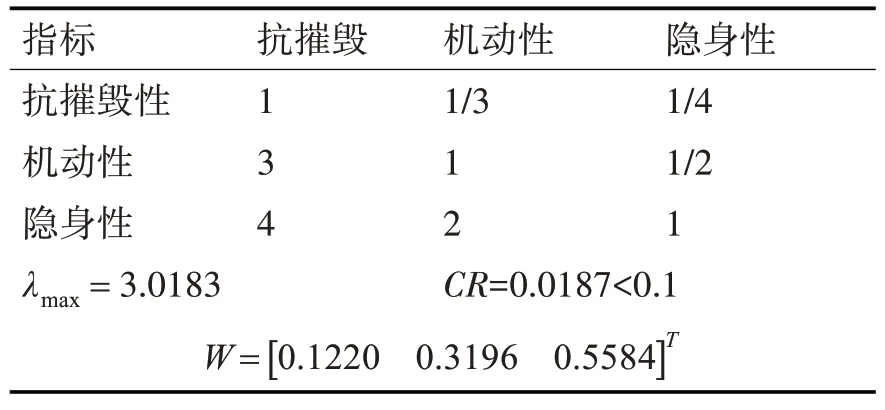
表4 生存性指标等级表
5 模糊综合评判
模糊综合评判有三要素[20]:
1)因素集:表示影响事物评判集的因素;2)判断集:表示影响事物评判集的等级;3)单因素判断:即对单个因素Ri的评判,得到模糊映射,从而确立一个模糊关系,得到单因素模糊矩阵:
根据无人机系统的复杂性,本文单因素模糊矩阵的确定采用专家评判方法。
根据图1 所示的无人机侦察效能评估体系确立模糊评判的因素集U。
将评判优劣等级划分为优,良,中,差。判断集为V={优,良,中,差}[21]。
根据专家评判获得获得指标层的单因素模糊矩阵RA,RB,RC。
6 综合评价
综合评价结果记为B,则B=,则可分别求出设计准则层、可靠性能、生存性能能力以及侦察性能的下层指标综合评价结果。
可以得到BA,BB,BC的值。
由Bi可得准则层模糊矩阵为
准则层的综合评价结果为
采用加权平均法对每个等级与权重分数赋值,以便于后续为不同方案进行排序。赋值如下:
V={优,良,中,差}={100,80,60,40}。
得到该无人机侦察效能的总得分为
S=B·V'=79.422
7 结语
本文基于层次分析法构建了无人侦察机侦察系统作战效能评估指标体系,并对传统的层次分析法进行改进,增加定量分析,弱化定性色彩。所建立的侦察效能评估模型具有一定的有效性和实用性,通过评估,可以对无人侦察机的作战效能进行定量评估。
影响无人机作战的因素很多,尽可能全面、准确地将其融入到作战效能的评估中来是接下来要努力的方向。
