基于GMM-SVM 算法的传感器缺失信号重构模型*

2023-06-04史柏迪庄曙东江志伟

计算机与数字工程 2023年2期

史柏迪庄曙东蔡鸣江志伟

（1.河海大学机电工程学院常州 213022）（2.南京航空航天大学江苏省精密仪器重点实验室南京 210093）（3.梅特勒-托利多测量技术有限公司常州 213022）

1 引言

在日益增长的物流需求和人工劳动力缺口矛盾面前［1～2］，自动化动态称重技术是物流业发展的必然之路。动态物流秤对于物体重量实时测量大多依赖于压感式压力传感器，作为典型机电复合系统，传感器受到多因素干扰，例如秤体传动电机产生的振动干扰［3］、货物在上秤时对压力传感器的冲击［4～5］当其与传感器固有频率一致时极易导致共振现象直接导致采样信号大量缺失；此外在实际工程运用中因电流与电压的不稳定，更是加剧传感器电信号丢失的情况。在当前大数据模式的发展［6］之下各行业均以数据的精确性与完整性作为行业发展的生命线。

缺失信号的补偿与重构一直为当前国内外学者研究的重点。基于统计学原理［7］的加权法、删除法、补插法因过程简单，算法时间与空间复杂度低，当前单片机、FPGA 等简易嵌入式开发设备中有着广泛的使用。M. V. Gashnikov［8］在2019 基于决策规则与样条插值算法提出一种缺失信号重构算法；Hussain［9］在2020 基于改进的EM 算法，对单边Lipschitz系统缺失信号进行了精确补偿。张丽君［10］在其学位论文之中，研究了高阶插值算法在缺失信号重构之中的可行性，且发现当信号缺失比例小于25%时，插值与线性回归算法精度较高。基于线性回归原理建立的补偿模型基于凸优化［11］原则可解得全局参数最优解，模型简单可靠。

当信号为多维变量或原信号缺失比例较大时，线性模型重构精度较低。近年随着机器学习算法的兴起，为缺失信号重构提供了更多可行的方案。虽机器学习算法类模型求解过程复杂，大多数情况下需要依赖群体启发式算法［12］求解局部最优解，但其强大的多元非线性拟合能力，对高缺失比信号的重构提供了可靠方案。L Kong［13］在2013 年提出一种基于压缩感知重构大量缺失数据的新方法。2015 年刘功生［14］在轴承传感器数据缺失的情况下基于隐马尔可夫模型，获取状态转移概率方程，实现了对缺失信号的补偿，与轴承故障的精确判断。Fenggang Wang［15］在2019提出一种基于稀疏学习与自回归AR 模型的缺失序列重构模型；2019 张婷婷［16］基于BP神经网络算法建立的重构模型当信号缺失率高达60%时依旧可有效重构信号。

上述机器学习模型本质上均为监督类模型，通过完备样本基于特定算法进行超参数更新从而有效学习样本特征降低信号重建误差。但上述模型当缺失信号比大于70%，特征过分残缺时重建精度均不大于60%，直接基于现有残余特征进行信号重构，模型极易达到性能上限实际重构精度难以达到实际使用需求。本文通过引入与压力高度相关的加速度信号特征，基于加速度信号使用GMM 无监督聚类寻找相似簇样本，随后使用高相关性样本进行残缺信号信号精确重构，从增加信号特征信息的角度来提高残缺信号重构精度。本模型分析对象为某公司的TW155 型动态物流秤，目前广泛运用于各大物流公司的计重收费系统，分析对象具有普遍性。

2 设计与相关性分析

2.1 正交试验设计

基于载重（M）、带速（V）与传感器采样频率（Hz）设计了三因素四水平的标准正交试验表1，为后期聚类与回归提供可靠样本集。

表中，为避免单一测量结果的随机干扰，各试验序号下进行100次测试，共计获取1600组样本数据。测试系统由前级、测量测与中间级三部分组成，货物上秤触发光电传感器时，压力与振动传感器开始采集数据，其采样频率为［366，720］Hz。因采样频率与带速不同，货物上秤采样信号长度各因素组合下各不相同，均取离开光电信号前150 个点作为采样信号。传感器安装于图1（b）所示位置。各组样本其数据格式如式（1）：

图1 测试系统

式中，i为样本索引（1 ≤i≤1600）；a为加速度矩阵向量分别为x、y、z 轴方向，n为压力传感器矩阵向量，s为信号长度本模型中即为150。

2.2 相关系数分析

由式（1）可知原始数据为［1600×7×144］的高维矩阵，即样本数目（n）为1600，特征指标为7，指标数目为144。数据维度较大，相关性难以直接进行，将各样本其基于特征取平均值将原始数据降维为［1400×7］，使用式（2）对其进行标准化处理。

式中，nor 为标准化数据；i 为样本索引，j 为指标索引。μj为第j 个特征均值，sj为其标准差。基于式（3）计算可得任意两个指标之间的相关系数。

式中，rij为指标i 与j 之间的相关系数，计算可得其相关性矩阵表2。

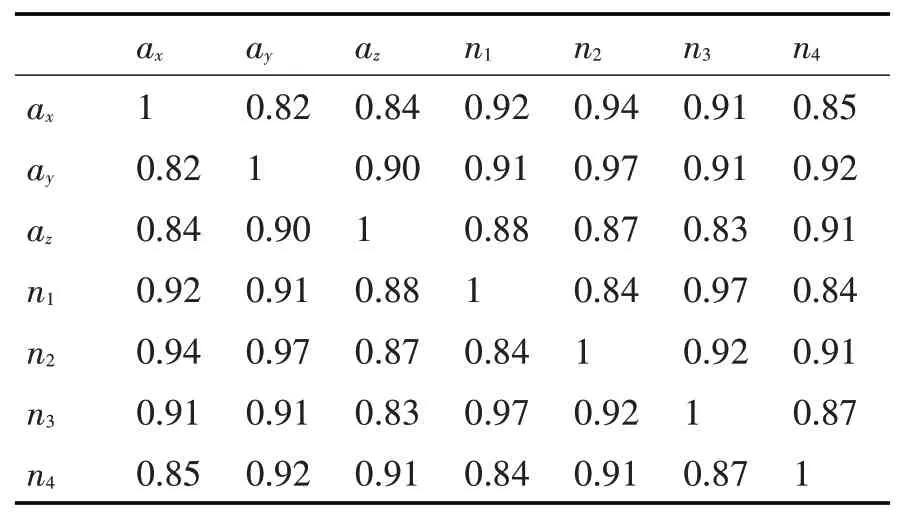
表2 指标相关性矩阵

易知当i=j 时，相关系数为1；且满足轮换相等性即rij=rji。三轴加速度与压力信号两两之间相关系数均大于0.8，呈现出高度一致性。

此外将三轴加速度与压力信号基于式（4）进行合成化处理可得合成加速度a及平均压力信号n。

皮尔逊相关系数式（5）对两个数据的位置以及尺度并不敏感，无需进行归一与标准化处理。被广泛运用于两个信号之间相关性检验。

式中，ai，ni为第i个采样点的合成加速度与压力值；μay 与μn分别为合成加速度a 与平均压力信号n 的均值，计算得其皮尔逊相关系数为0.94。

3 重构模型的建立

3.1 基于加速度的高斯混合聚类

相关系数与皮尔逊相关性检验表明：在TW155物流秤动态测量过程中振动与压力信号呈现高度相关性。当压力信号高度缺失时，可用聚类算法基于现有加速度信号从表1 完备数据组中，寻找高度相关样本簇，实现对压力信号实现精确补偿。传统k-means［17］、LVQ［18］等聚类算法基于原型向量来建立样本聚类结构，高斯聚类［19］基于高维多元高斯分布式（6）来对聚类数据的原型进行表达。

式中，μ为均值向量矩阵。R 为相关系数矩阵其计算方式与式（3）相同；n 为特征维数。易知在加速度信号x 完备的情况下，高斯分布完全由μ、R 参数决定，将式（6）简写为p（x|μ，R），可定义混合分布式（7）：

式中，该分布由k 个混合成分组成，μi、Ri为该混合成分所对应参数；a 为混合系数。令随机变量zj为第j 的样本xj的高斯混合成分，其参数μi、Ri基于该迭代轮次t 样本计算可得，混合系数ai的求解则基于贝叶斯定理可得其后验概率分布式（8）：

式中，计算得xj在第i 个高斯混合分布下的后验贝叶斯概率，为简化求解过程，将其记为γij。在上述条件之下高斯聚类将样本集D 划分为k 个簇C=｛C1，C2，…，Ck｝，各样本xj由式（9）确定：

由上述式（6）～（9）可知，高斯混合使用高斯概率分布来对模型进行划分，对于参数μ、R、a可得其极大似然估计函数式（10）。

式（10）采用最大期望算法（EM）进行迭代求解可获得较好精度，在文献［20］已经给出详细求解流程，结合式（6）～（10）得GMM算法流程：

GMM算法流程

Input:sample set D;Gaussian mixture fraction k

Processing：

1.Initialization {(a，μ，R)i|1 ≤i≤k}

2：for t= 1，2，…，T do

3：for j= 1，2，…，m do

5： end for

6：for i= 1，2，…，k do

7： Calculateai，μi，Ribase on EM algorithm

9： end for

10：update {(a，μ，R)i|1 ≤i≤k}

11：end for

12：Ci=∅(1 ≤i≤k)

13：for j=1，2，…，m do

15：end for

Output:C={C1，C2，…，Ck}

表中，D 为表1 获取的加速度样本集；高斯混合成分数目k 即为聚类数目，m 为样本数目；T 为迭代次数；最终输出为划分完成的聚类样本C；选用轮廓系数式（11）作为模型与后续重构聚类评价指标。

式中，a（i）为样本i 到同簇其他所有样本的平均距离即为簇内不相似度；b（i）为样本i 到其他簇Cj内所有样本的平均距离即为簇外不想似度；s（i）约接近1 则该样本聚类合理；此外定义S 为所有样本的平均轮廓系数，用来度量模型整体性能。

经过枚举k 发现当其取值为15 时，轮廓系数S在区间［0，1］达到极大值为0.8476，图2为对表1中完备样本划分为15类时基样本聚类结果图。

图2 聚类效果（k=15）

图中，x，y，z 三轴加速度为防止因数值波动造成聚类误差表1中各类样本均进行了归一化处理。

3.2 基于GA-SVM的信号重构模型

当压力信号n 出现缺失时，使用加速度信号a输入上述GMM 模型即可找到其相似样本完备簇C，通过提取其压力样本特征来重构残缺信号。

GMM 模型中完备样本数目为1600，神经网络模型虽拟合性能良好，但当样本容量较小时，即使引入正则化依旧限极易产生过拟合现象，造成重构精度较差。支持向量机通过核方法将低维不可分数据映射至高维空间，此外基于交叉验证原则求解决策边界在小样本容量下拥有极强的鲁棒性与泛化性。SVM 模型中核函数k（xi，yi）；正则化系数C，相关系数co（poly 与sigmoid 核函数时生效），多项式最大项次n；软间隔系数to1；作为超参数其初始值设置直接影响模型后续精度。

SVM模型超参数的确认，作为浮点数与整数混合规划问题，无法基于凸优化原则获得最优解。使用GA 算法寻找局部最优解。核函数k（xi，yi）采用排列编码进行选择其对应关系表3；C 搜索区间为［0，1］，co 搜索区间为［0，10］，tol 设置为［10-3，10-1］，上述浮点数均采用格雷编码。最大项次，使用整数编码。

表3 核函数对应表

表中，高斯核中σ带宽取1，多项式与Sigmoid核中d与β为上述超参数n，该参数在其他内核函数中为无效参数。设置种群数目N 为50，进化次数T为100；特征维度D为5，交叉阈值CR为0.1。

本GA-SVM 模型的SVM 模块使用sklearn 工具箱进行搭建，GA模块基于如下步骤进行：

1）寻找簇样本。基于待重构信号的加速度a，使用GMM 算法寻找其压力信号所属簇C，并将其改写为待重构的n 记为输入特征X，原始完备样本簇中压力信号Y作为输出。

2）初始化参数。种群NP 由N 个二进制编码的个体pop={k，C，co，tol，n}组成。

3）迭代准备。基于种群NP，使用sklearn 建立对应SVM 模型，并计算种群初始适应度y，对最优适应度个体pb进行记录。

4）遗传进化。对种群NP基于精英策略进行选择（赌盘法）、交叉、变异式（11），同时将满足精度的个体加入下轮循环，不满足精度的个体进行剔除。

5）迭代终止。当迭代次数达到上限T 时，输出NP中最优个体，并基于此参数建立SVM模型。

6）模型训练。基于五折交叉验证原则使用样本使用样本（X，Y）对SVM模型进行训练。

7）信号重构。使用残缺压力信号a 输入SVM模型，对残缺信号进行重构输出。

选用平均均方误差作为性能评价指标，图3 为缺失比例为0.6时的GA寻优误差波动。

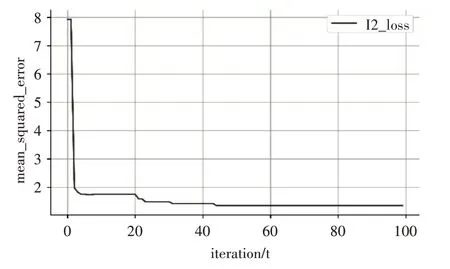
图3 GA参数寻优

图中，当迭代次数达到40 时，模型已经收敛。对100次的最优参数pb按字典形式进行导出：

式中，当缺失比例为0.6 时，查表3 选用rbf 高斯内核，相关系数co，最大项次n 均为无用系数。选用0.1 为分位点，当缺失比例为0.7、0.8 与0.9 时，可得类似误差曲线。SVM 模型超参数确认后使用SMO算法训练，在5 折交叉验证原则下训练误差收敛或验证集误差发散时迭代终止。

4 模型测试

测试集样本使用三级传动系统图1 产生，对圆盘状43.137kg 货物在带速90（m/min），采样频率400（Hz）下进行100 次压力信号测定，后使用random 函数对采样的150 个数据点随机依次剔除60%、70%、80%、90%压力信号数据点。使用未经聚类的GA-SVM、GA-BP 进行性能对，测试计算机配置为 CPU：i7-9750H、RAM：16GB、GPU：GTX1660Ti。选用运算时间（s）、平均绝对误差式（13）、最大误差项式（14）及校正决定系数式（15）评价信号重构修复后与原信号的相似度。

式（13）～（15）中，n 为样本数目，i 为其索引；k 为一个样本所包含的信号点数，j 为信号点索引；f 为模型的重构输出y 为压力传感器真实观测量；调整绝对系数通过加权考虑输入特征数p，有效避免决定系数R2对样本数目n的波动敏感的问题。表4为各模型的性能度量。

表4 模型性能测试

表中，GA-BP 为双隐层结构，神经元数目依次为150、60，使用Adam 优化器进行训练；经过样本聚类处理的GA-SVM 相对GA-SVM、GA-BP 模型平均绝对误差与最大误差显著降低，且调整绝对系数最大有着最好的拟合精度。GA-BP模型基于pytorch 框架搭建，使用了cuda 进行GPU 并行加速运算，时间复杂度最低。但因受限于样本数目，信号重构修复精度并不理想。当信号缺失率低于80%时，对原测试集信号平均解释度为0.956，误差可控于5%。图4 为当缺失比例为90%时，各模型实际重构修复效果。