金沙江下游区间来沙驱动因子分析及产沙预测模型
2023-06-03谭寓宁刘怀湘陆永军
谭寓宁,刘怀湘,陆永军,3
(1. 南京水利科学研究院水文水资源及水利工程科学国家重点实验室,江苏 南京 210029;2. 四川大学水力学与山区河流开发保护国家重点实验室,四川 成都 610065;3. 长江保护与绿色发展研究院,江苏 南京 210098)
随着近年来长江上游水电开发的快速推进,金沙江流域水库群的蓄水拦沙导致剧烈的水沙调整,其中下游区间乌东德、白鹤滩、溪洛渡和向家坝4级巨型水库的影响尤为显著。向家坝、溪洛渡水库分别于2012年10月和2013年5月蓄水运用,蓄水初期向家坝下游年输沙量在2 a内即锐减至不足1998年前输沙量均值的1%[1]。2011年以来金沙江流域水库群年均总拦沙量达1.92亿t,其中2013—2016年溪洛渡和向家坝两库年均拦沙量即占1.05亿t[2]。
水库拦沙淤积将影响长期运行效益,其中入库沙量是决定淤积总量的控制性因素。金沙江流域来水来沙不均衡,水沙异源等现象十分突出[2-4]。攀枝花和屏山水文站分别为金沙江下游入口、出口控制站,两者区间内支流来沙量可占入库总沙量的近80%。以区间为主的来沙特征将显著影响库区输沙过程、淤积形态及优化调控思路。现有研究对该区间来沙往往基于少量支流水文站的观测资料进行简单估算[2,4-5],较为精细化的研究非常缺乏。金沙江下游流域面积达500 km2以上的支流有32条,只有少数建有水文站,部分站点还存在时间序列短、位置远离河口等问题。已有数据表明,各支流输沙模数在3个量级内变化,单位面积产沙能力差异极大,无法简单推算无资料支流的来沙。因此现有研究相对不足,难以认识区间来沙全貌,从而也将影响对干流库群泥沙淤积的预测能力。
区间来沙问题实际上主要为流域产沙的问题。山区河流泥沙有多种来源,包括降水导致的片蚀、细沟侵蚀和滑坡、泥石流、崩岸等重力侵蚀等[6-8]。影响山区流域产沙的因素如气候、植被、地形等会由于当地的土壤侵蚀和泥沙输移机理而呈现出不同的驱动因子组合[9-10]。再加上这些地区气候、下垫面条件复杂且存在相互影响[11],特别是支流小流域对各因子扰动的响应比大流域更为直接、迅速[12],对于该类地区实际泥沙特性的研究更有难度。利用数学模型方法可有效评估流域产沙能力和预测扰动影响下的泥沙响应[13-14]。为此,获取驱动因子与产沙之间的定量关系并择优进入模型搭建是该方法中的核心问题。过去研究中通常使用直接线性回归逐一确定因子间关系,以及通过偏最小二乘回归(Partial Least Squares Regression,PLSR)法对全部因子回归得到经验模型[15-17]。但该类回归方法可能无法揭示因子间的实质联系,而且输入过多的因子变量还会导致对因变量的重复解释。此类模型体量臃肿,实际应用中需要大量的参数化和校准,在资料匮乏的山区流域通常难以适用。因此,只有消除冗余因素、降低参数维度、识别和筛选出目标主控因子,才能合理认识目标流域的产沙机制并搭建产沙预测模型。
明确金沙江下游区间泥沙全貌时空特征,辨析泥沙来源格局成因与主控因子,对合理利用管理与调控流域泥沙具有重要意义,可为金沙江下游巨型梯级水库运行方式的进一步优化提供依据,也可为高强度人类活动影响下长江流域水沙通量变化研究奠定基础。本研究基于金沙江18个支流水文站观测数据,采用Spearman秩相关方法揭示因子集内部以及与产沙之间的矩阵关系,通过偏相关方法对因子集进一步降维,识别能够反映区间来沙特性的多因子组合,采用PLSR-多元双重回归法构建山区流域输沙模数预测模型。
1 研究区域
金沙江多年平均悬移质输沙量为2.47亿t,约占长江上游输沙量的47%,为长江流域重要沙源。雅砻江汇口至宜宾为金沙江下游(图1),全长约768 km,流域面积约为8.6万km2。降水主要集中在5—10月,可占年降水的80%以上,汛期平均降水量为855 mm。气温差异明显,中部山区5—10月平均温度可低至8 ℃,而干热河谷地区温度可达25 ℃。山高谷深的地势使得区域内热量和水分条件都明显垂向分化,形成了垂直气候带。区间内如美姑河、黑水河等(图2)众多支流均具有典型山区河流特征,河道剧烈下切,河谷最大深度可达约3 100 m,形成了典型的“V”型侵蚀河谷地貌。流域内崩塌、滑坡、泥石流等重力侵蚀频繁,产沙丰富。

图1 研究区域概况Fig.1 Distribution features of the study area

图2 金沙江下游典型支流现场照片Fig.2 Typical tributary site photos
2 研究方法
2.1 数据来源
本研究中,支流水文站(16个位于金沙江下游,2个位于中游段出口区,见图1和表1)泥沙观测数据来源于《长江流域水文年鉴》,选择其中水电开发影响较小时间段(表1)的天然泥沙序列作为训练集数据。地形数据来源于30 m×30 m分辨率ASTER GDEM(https:∥urs.earthdata.nasa.gov),通过处理得到空间尺度、河流水系等。土地覆被数据来源于资源环境科学与数据中心(http:∥www.resdc.cn)1 km分辨率土地利用遥感监测数据集(1980年,2010年),根据第二次全国土地调查土地利用/覆盖分类体系,按照一级类型进行重新合并得到。气温、降水数据来源于国家地球系统科学数据中心(http:∥www.geodata.cn)利用原始气象站点资料插值生成的1 km×1 km分辨率逐月平均数据集(1970—2018年,取支流泥沙资料对应的5—10月数据)[18],在该数据库生成5 km×5 km分辨率逐月归一化植被指数(INDV)遥感数据集(1982—2018年)。所有数据产品均经过严格复合审查,精度得到保证。

表1 支流水文站数据序列
2.2 因子选择
选取地形、气候、土地覆被和空间尺度几类因素[6,19-21]的原始数据作为因子集(表2),有助于明晰自然环境条件与悬移质来沙的直接因果关系,同时也降低了后续建模参数要求。

表2 选用因子基本概况
2.3 分析方法原理
2.3.1 Spearman秩相关分析
Spearman秩相关是一种有效非参数统计方法,适用于不是正态双变量或总体分布未知的资料[3,11]。计算公式如下:
(1)
式中:R为Spearman秩相关系数;di为变量X第i个观测值xi的秩和变量Y第i个观测值yi的秩之间的差值;n为样本容量。R越接近1,说明两者间相关性越大。相关系数检验p<0.05时相关性显著,p<0.01时相关性极显著,其余表示不显著。
偏相关方法量化去除控制变量影响后某2个选定变量之间的关联程度[19,21],原理是分别对控制变量和选定变量进行回归,然后计算这2个回归结果残差之间的相关性。
2.3.2 PLSR回归分析

Q2=1.0-SE/SS
(2)
(3)
(4)
式中:SE为预测误差平方和;SS为残差平方和;N为成分ti的个数。
3 产沙异性归因分析
3.1 泥沙不平衡分布格局
悬移质输沙量(W)和悬移质输沙模数(M)是比较不同尺度流域产沙能力的常用指标[10,22]。对于小流域山区河流,即使环境条件稳定时产沙随机性也较大,即年际变化较大,因此,从多年平均尺度进行分析更为准确。金沙江下游泥沙分配极不均匀,如牛栏江大沙店站(5-DSD)年输沙量达1 112万t,远高于其他水文站(图3(a)),但一定程度上是由于其集水面积较大;与之相比图3(b)的输沙模数分布更能反映研究区域内单位面积产沙能力,各地区之间也更具有可比性。如昭觉河(1-ZJ)、黑水河(4-NN)的输沙量远小于牛栏江(5-DSD),但输沙模数反而略大于后者。

图3 支流水文站集水区实测泥沙指标分布Fig.3 Distribution of observed sediment index in catchments of tributary stations
3.2 各因子类别内部降维
单个因子无法完整预报流域产沙,但使用过多因子又会导致重复解释的问题。因此,在完整地定量化研究因子-产沙关系前需先进行降维处理,即去除代表性弱、关系不大或是可被替代的因子。开展Spearman秩相关分析得到表2中因子与W、M以及各因子之间的矩阵关系(图4,*代表p≤0.05,**代表p≤0.01),然后从侵蚀输沙的物理意义出发,在地形、气候、土地覆被和空间尺度几大类别中筛选各类别的代表性指标。
(1) 地形类别。各坡度因子(Smean,S8,S18,S25)内部之间的相关系数高达0.91~0.97,即研究区域内各坡度占比具有较高的一致性,因此过多的坡度因子在指标信息上是冗余的。S8与M的相关性最好(R=0.64),S18次之(R=0.61),而S25和Smean对于M的解释能力较为一般(R=0.53)。由于各集水区内部坡度的分布差异性较大,单一的平均坡度Smean影响产沙的物理机制相对不明确是可以预见的,而中坡度占比S8则拥有预报M变化的相对优势。
高程因子中Hmax与M相关性最显著(R=0.83),其次是相关性明显弱一级的Hmean(R=0.58)及Hmin(R=-0.12),且Hmean与Hmax之间本身自相关(R=0.72),因此,Hmax可替代Hmean。地形对于流域产沙的影响由多过程耦合而成,从侵蚀源头来看,高海拔(高Hmax)山区流域内通常也具有极大的落差,对应的是流域内坡面更大的潜在势能、更低的地表入渗率和更大的产流量,产沙能力相应增强[17]。从泥沙输移的角度来看,高山地区众多的坡面(高S8)减小了侵蚀泥沙颗粒随后沉积的概率,所以坡度因子直接控制的是流域泥沙的沉积汇过程。从降维意义而言,可选取S8与Hmax的参数组合来替代其他地形因子。
(2) 气候类别。T与M具有极显著的负相关性(R=-0.81),而P与M的关系则相对一般(R=0.59)。气温与产沙之间的强关系存在多方面原因:首先气温关系到降雨概率、雨时、落区以及范围和强度大小等直接影响侵蚀源[21],如图4中T与P的负相关性(R=-0.70)量化反映了研究区域内明显的干-热与冷-湿分布差异(图1);其次,T与Hmax的负相关性(R=-0.64)也说明气温通过地形地理条件关系到产沙能力。由于P很大程度上能被T反映,因此,选取T代表气候因子。
(3) 土地覆被类别。fa与M相关性极差,而ff、fg与M的相关性近似处于同一等级(ff:R=-0.45,fg:R=0.57)。本质上草地和林地都抑制了土壤侵蚀,但草地水土保持能力远弱于林地[23]。fg与M的正相关性很大程度上归结于研究区域特性:土地覆被以林地和草地为主,有14个集水区的林地、草地占比总和超过70%,ff与fg存在一定此消彼长的现象(R=-0.52)。从土地覆被与其他因子之间联系也可看出,Hmax、T与fg分别为正相关(R=0.42)、负相关(R=-0.53),与ff则相反,即形成了可见的二元空间分布格局:高海拔、低温情况下草地优势,林地劣势,反之亦然。也就是说,fg与M的正相关性是由抗侵蚀能力更强的林地减少所导致,这也从侧面证明了单因子回归分析的局限性。因此,选取更符合物理意义的ff代表土地覆被因子。
(4) 空间尺度类别。FF与M相关性极差,因此,只选取相关性更好的A作为该类别的代表。

图4 水文站集水区多因子Spearman秩相关分析Fig.4 Spearman rank correlations between factors
3.3 因子类别间降维
基于筛选因子开展偏秩相关性分析,最终分离出能够定量反映产沙多过程的驱动因子组合。如图5所示,输入S8、Hmax、T、ff、A共计5个因子,然后将显著性检验结果p作为选择控制变量阈值(优先p<0.01),按照偏相关系数大小顺序逐步筛选出余下最能解释M的因子变量,直到偏相关系数均不通过显著性检验为止(即图中所有变量p>0.05,为空心圆),此时表明余下自变量已不足以解释因变量变化,输出6个驱动因子组合。
Hmax作为单因子对M变化已有一定解释能力。相对地控制住T后,此时A与M表现出了明显的正相关性。类似地控制住S8后M与ff之间负相关性明显加强,说明流域内中等坡地与产沙的强关系掩盖了林地对M的抑制作用,去除前者影响时后者的相关性有了大幅提高。在S8组里得到了4个因子组合S8-ff,S8-T-A,S8-T-ff-A和S8-Hmax-ff。不难看出,图5一阶控制和二阶控制中M—A的正相关性均在控制T后显现,说明当山区流域总体上侵蚀潜能接近时,流域间存在明显的M—A尺度效应。以上结论都是传统的单因子回归方法所无法反映的。
一些研究认为M—A相关是因为随着集水面积的扩大,类似于谷底这种泥沙易沉积的缓坡比例相应增加,因此M会随着A的增大而减少[10]。但本研究中各级坡地占比与A没有表现出明显相关性(R=0.06~0.25,图4),由于河道下切剧烈、遍布“V”型河谷,缓坡宽谷段未随流域面积增大。究其原因是由于A与Hmin负相关(R=-0.76),因此,在控制T的前提下,A增大对应于Hmin减小与流域内高差增大,提高侵蚀势能与产沙,故此时M—A呈正相关。

图5 偏秩相关分析及驱动因子组合结果Fig.5 Partial rank correlation analysis and factor combinations
4 产沙预测模型
4.1 PLSR回归模型
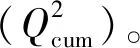

表3 PLSR回归分析结果
4.2 多元回归模型
考虑到M与自然环境因素之间的非线性关系,因此,对比线性模型4#进一步建立相似环境下的多元回归模型。按照偏相关分析(图5)的控制顺序,首先测试S8-M的多种函数拟合结果发现指数形式拟合优度(R2=0.43)最好,以此为基础进一步评估结合T、A多种形式的多元回归效果(图6(a)—图6(c))。经过比对发现T和A分别取指数和乘幂形式的拟合效果最佳(图6(b)),此时模型足够解释约86.4%的M变化性,但各模型在靠近预测结果(M*)极值时失稳(图6(d))。这是由于泥沙训练集主体含有相当部分的重力侵蚀占比,未修正前的模型会高估少数支流泥石流、滑坡水平。如当输沙模数很大时,重力侵蚀可能已达到上限,其余侵蚀产沙比例上升,此时模型预测值偏高需向下修正。假定修正参数k为实测值与预测值之比,对k和M*拟合得到修正系数公式(图6(e))。模型形式如下:
Mpre=kM*
(5)
式中:Mpre为修正后的预测输沙模数;k为修正系数;M*为未修正的预测输沙模数。其公式如下:
M*=exp(0.7S8-1.56T)A0.28
(6)
(7)
过去类似模型大多止步于统一的线性或幂函数形式,并没有对模型进一步优化[15-16]。模型7#R2与ERMS明显优于模型4#结果。其中,T可反映流域总体潜在侵蚀源大小,S8则主要描述过程中沉积汇可能,A则与流域内泥沙来源、侵蚀类型组成等部分特性有间接联系,因此,本模型也能反映流域的主要侵蚀-输沙特征。

图6 多元回归模型拟合修正Fig.6 Scatters of multivariate regression model results
4.3 模型验证与对比
对于金沙江下游干流河段,在向家坝、溪洛渡蓄水前(2012—2013年)可近似看作多年冲淤平衡的自然状态,即区间各支流来沙总和按区间出、入口水文站输沙量差值来估计。分别选取攀枝花站(及雅砻江桐子林站)、华弹站和屏山站多年平均输沙量资料作为实测值对以上模型进行验证,并通过2时段对比检验模型在时程上的预测精度。表4显示,华弹—屏山区间模拟值与实测值总体吻合较好。攀枝花—华弹区间存在输沙量异常高的小江等支流,考虑到该类支流无水文站泥沙资料,本研究根据东川泥石流观测研究站估算小江年输沙量来得到区间来沙总量,模拟结果也与攀枝花—华弹实测值接近(表4)。除了区间来沙的模型计算总量符合干流实测值外,图7显示,模型对不同时段划分后的产沙计算值也与各支流对应时段的实测值吻合较好。

表4 金沙江下游区间来沙量模型验证
金沙江下游目前还没有系统性的产沙模型研究,仅有部分针对土壤侵蚀和产流的模拟[24-25],不易实现例如本模型对区间来沙的估算。相比于对金沙江中游流域无资料地区进行的类似产沙模拟研究[26],模型7#所需输入数据更易于获得,输出结果表现良好,避免了采用其他模型时遇到的诸多限制。
现有产沙预测模型也难以直接应用到本研究区域。如图8所示,使用ART模型[27]或更新后的BQART模型[28]往往会高估中小型流域M值[29]。该类模型侧重于大中型流域(流域面积为104~106km2)泥沙通量的估算,而研究区域18个集水区平均面积仅2 780 km2,引入时还需降尺度处理。相比之下,结合土壤侵蚀模型(RUSLE)与陈治谏等[30]所得泥沙输移比(RSD)推算出来的结果稍好。但RSD在各个子流域之间各不相同,由于低产沙带输沙难度更大,在计算中套用目前仅有的流域均值会高估该区域M。对比发现本研究得到的模型7#表现最好,因此,能够有效地模拟流域范围内无资料地区的M。

图7 划分时段后的模型计算值验证Fig.7 Model validation for two periods
4.4 泥沙时空变化格局
根据模型对金沙江下游整个区间多年平均M的空间分布进行推算(图9)。参照图3(b)发现,除了已有泥沙资料的少量支流外仍有大量未监测高产沙地带,主要集中在白鹤滩和溪洛渡两大巨型水库库区,其M明显高于其余地区特别是入口近攀枝花和出口近宜宾一带。

图9 金沙江下游区间多年平均输沙模数分布Fig.9 Predicted M distribution of the study area
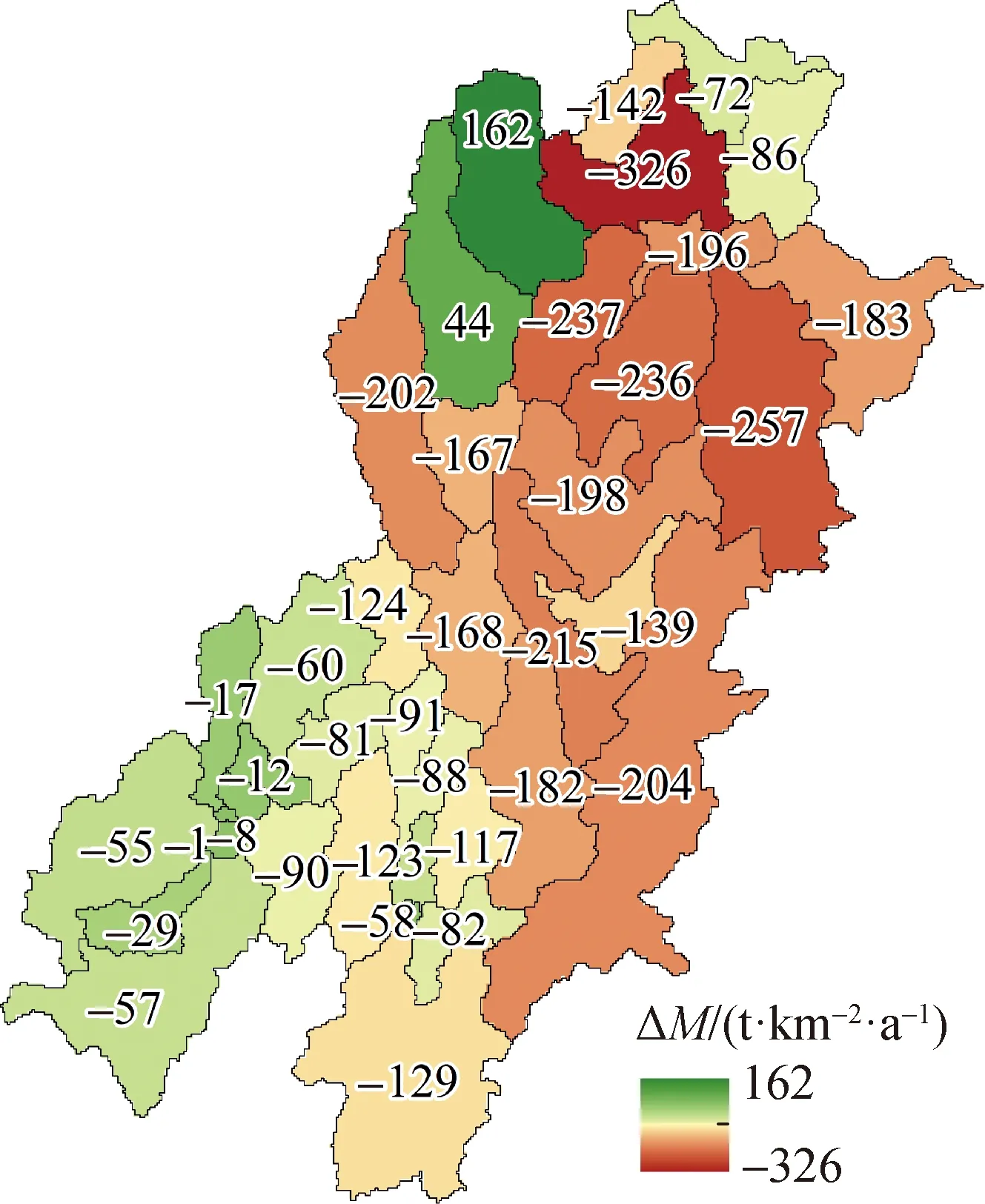
图10 2007—2018年相对1970—1986年输沙模数变化Fig.10 Variations of M from 1970—1986 to 2007—2018
时间变化上,由图10可以看出,大部分地区M近年比20世纪七八十年代明显减小,减小幅度一般在50~300 t/(km2·a)。有学者统计得出1991—2005年金沙江下游“长治”工程(包含下垫面治理及塘堰、拦沙坝等水保工程)水土流失治理减沙效益仅为4.9%,尤其对重力侵蚀效果不佳,不是支流来沙减少的主因[31],即这一趋势很大程度上是自然条件变化导致。Li等[9]在地理位置相邻的西江流域中同样得到了长序列下的M减小趋势,并且指出升温刺激了植被长势,INDV增加。经本研究统计,金沙江下游INDV在2个时间段间也升高了9.8%~20.7%,研究区域温度的升高可能提供了更好的植被发育条件,对产沙的抑制作用也因此增强。同时,中部高产沙区的减沙程度总体上高于出、入口地区,即研究区域产沙的空间不均衡性近年来有所削弱,若自然条件变化趋势不变则有可能进一步均衡化,减轻白鹤滩、溪洛渡水库淤积压力。
相关研究结果有利于区间内泥沙溯源,进而对干流乌东德-白鹤滩-溪洛渡-向家坝梯级库区支流来沙与泥沙淤积的不均匀分布进行精细化研究,如支流河口拦门沙等,也有利于为梯级水库的调度运行提供参考。
5 结 论
本文采用金沙江18个支流水文站多年泥沙资料,分析流域泥沙和地形、气候、下垫面、空间尺度及人类活动等因素的关系,对金沙江下游区间多年来泥沙分布格局、驱动因子以及变化趋势进行探究。主要结论如下:
(1) 明晰了能够解释金沙江下游来沙异性格局的多个自然环境因子,揭示了各因子对流域产沙的潜在影响以及各因子自身的变化独立性与信息冗余程度,弥补了单因子回归分析等传统研究方法的不足。
(2) 分离出多个关键产沙驱动因子组合,继而获得了与类似研究相比拟合优度更高的因子和产沙关系模型。其中,以气温、8°以上坡度占比、集水面积为变量构建的预测模型能够解释约92%的输沙模数变化性,模型参数需求较低且经验证预测精度良好,在时空尺度上都具有稳健表现。
(3) 本文模型计算结果表明,金沙江下游无实测资料区间输沙模数空间分布极不均衡,在87~1 189 t/(km2·a)间变化,其中高产沙地带主要集中在白鹤滩和溪洛渡两大巨型水库区间;同时,研究区域输沙模数近50 a来减少约50~300 t/(km2·a),空间不均衡性有所削弱。本文可为解决类似的山区支流泥沙与水库淤积计算问题提供参考。
