地震作用下边坡代表性滑动面识别及系统可靠度确定

鲍俊文,赵少飞,李萍萍,刘子源

(华北科技学院,北京 东燕郊 065201)

0 引言

地震作用下的边坡破坏是地震活动中常见的地震地质灾害类型,不仅数量多、规模大,而且危害性极大,常会对人类活动造成特别严重的损害[1]。地震作用下边坡稳定性分析,主要采用拟静力方法[2],即将地震作用简化为水平方向和垂直方向恒定的惯性力施加到边坡上,通过极限平衡法等方法确定其安全系数。虽然拟静力法计算结果有一定误差,但因其计算简便、实用性较强,被广泛应用[3]。由于土性参数往往变异性较大,而且随着空间位置不同而变化,应充分考虑这种不确定因素对地震作用下的边坡稳定性的影响。为了反映土参数的空间变化这一特点,需要采用随机场理论[4]对边坡稳定性相关的土的物理、力学参数进行客观描述。目前,建立边坡随机场的方法包括局部平均法、中心点法、Karhunen-Loeve (K-L)展开和协方差矩阵分解法等[5]。史良胜等[6]比较了这几类随机场离散方法,得出K-L展开方法在离散土体参数各向异性随机场方面具有较好的收敛性。

由于土体参数的不确定性等原因,边坡往往会沿多个潜在失稳滑面破坏[7],即存在多个失效模式,此时采用单一临界滑面对边坡可靠度进行分析往往会极大地低估失效概率[8]。为了能够更真实地反映边坡的安全水平,许多学者对多失效模式的边坡可靠度进行计算,即进行边坡系统可靠度的研究[9-10]。应用边坡系统可靠度传统计算方法(以下简称“传统方法”)时,需分别计算出每个失稳滑面的可靠度,根据各个失效模式的串联关系得到。这种方法常常需要大量的计算且效率不高。而且部分潜在滑动面由于同时穿越相同土层,意味着它们相互之间具有相关性[11]。这样一些潜在滑动面对边坡可靠度的贡献完全可以由其它滑动面有效代替,通常将这些可以代表其它滑动面贡献的滑动面称为这组滑动面中的代表性滑动面[12]。因此,基于代表性滑动面进行边坡系统可靠度分析,可极大地提高计算效率,一些学者尝试代表性滑动面对边坡系统可靠度进行分析[10,12-14],但是,在筛选边坡代表性滑动面时需要提前选定相关系数阈值,并进行重复性计算,总体来说其计算过程较为繁琐且效率不高。为了解决这一不足,Wang等[15]和徐哲等[16]尝试利用机器学习中k-means聚类算法筛选出边坡代表性滑动面,结果表明k-means算法对于识别代表性滑动面比传统方法比较有效。然而,在地震作用下的边坡稳定性分析中,还没有研究如何有效确定代表性滑动面,并确定系统可靠度。

本文对一黏性土质边坡,采用拟静力法对地震作用进行简化,设计基本地震加速度从0.0到0.4g(g为重力加速度),通过K-L展开离散黏聚力和内摩擦角生成边坡随机场,采用蒙特卡罗法计算地震作用下边坡各个潜在滑动面的失效概率,利用k-means法识别代表性滑动面进行系统可靠度计算,并与传统系统可靠度算法进行对比。

1 边坡代表性滑动面确定及系统可靠度计算

1.1 边坡代表性滑动面确定

聚类算法k-means是一种无监督学习,广泛应用于数据统计、机器学习及数据挖掘中。k-means算法简单而且计算速度快,其思想是选择几个聚类中心,然后将样本数据代入其中计算其与聚类中心的距离,不断重复直至满足收敛要求。k-means算法具体步骤[19]如下:

(1) 选取聚类个数k值。

(2) 在数据xi(i=1,2,…,n)中随机选取k个数据,作为k个类别的均值mj。

(3) 计算每个数据点xi(i=1,2,…,n)到mj(j=1,2,…,k)的欧氏距离dij。对于某个数据点xi,归类于最小值dij对应的第j类。

(4) 计算各组内数据的均值mj(j=1,2,…,k),作为这个组新的均值。

(5) 循环第(3)、(4)步,直到先后两处均值点不变或差别在误差范围之内。

流程图如图1所示:

1.2 边坡系统可靠度计算

边坡可以看成由多个子系统构成。由于边坡任意一条滑动面发生滑动,边坡整体就会发生破坏,因此将边坡整体当作一个串联系统进行系统可靠度的计算。

假设一个串联系统由n个子系统构成,串联系统的系统失效事件为n个子系统失效事件的并集,故

P(E)=P(E1∪E2∪…∪En)

(1)

式(1)表明,当子系统失效事件彼此互斥时,串联系统的系统失效概率即为各子系统失效概率之和。串联系统不失效事件是每个子系统都不失效事件的交集,因此有

(2)

如果各子系统失效事件之间是统计独立的,公式(2)可写为

(3)

所以系统的失效概率可按下式计算:

(4)

(5)

采用k-means聚类确定代表性滑动面的系统可靠度计算流程,计算流程如图2所示:

图2 代表性滑动面的系统可靠度计算流程

2 算例分析

地震水平作用和竖向作用对边坡稳定性的影响是不同的,本研究重点在于分析边坡地震作用下边坡系统可靠度的影响,不考虑竖向地震作用的影响。设计基本地震加速度从0.0到0.4g,分别对应着无地震作用到抗震设防烈度IX度。

以某一黏性土质边坡为例,边高h为10m,高宽比为1∶2,坡脚以下4m处为基岩,如图3所示。土的天然重度γ取18kN/m3,水位下有效重度γ′为9kN/m3。边坡的初始水位在坡顶下4m、坡底下2m位置。

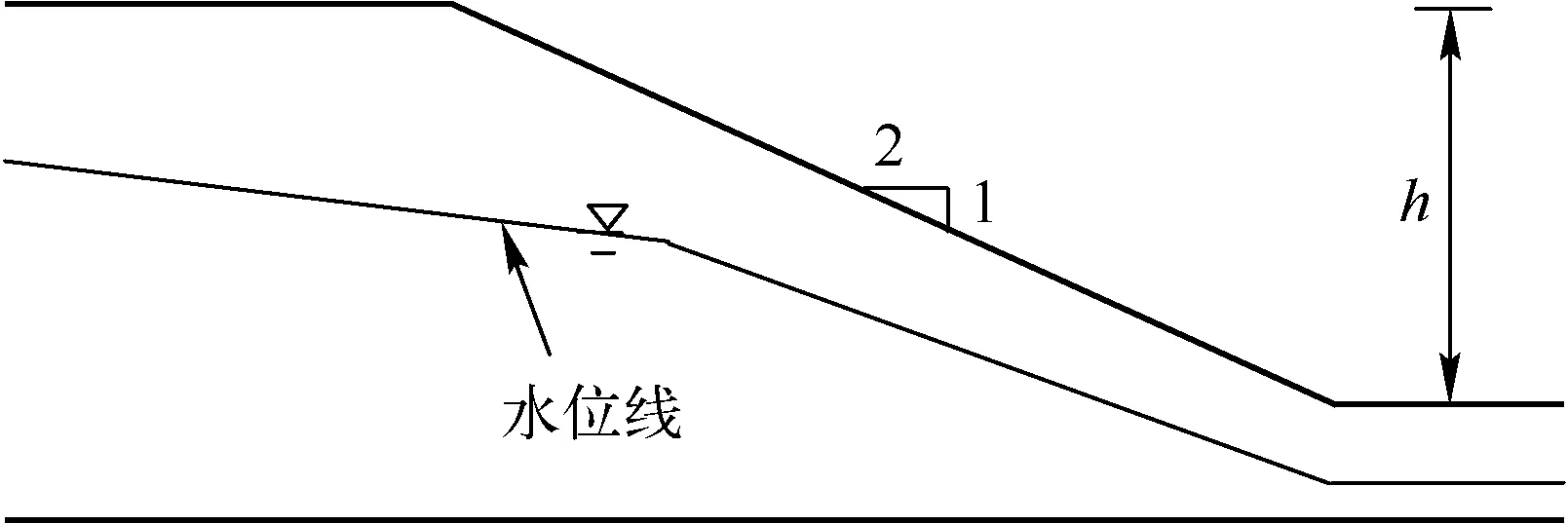
图3 边坡计算模型

边坡中土的黏聚力、内摩擦角服从对数正态分布,均值μc为10kPa,μφ为25°,均方差σc为1kPa,σφ为2°,空间相关距离相同,水平相关距离δh为40m,垂直相关距离δv为2m。

利用K-L展开,对黏聚力和内摩擦角分别进行离散,建立相应的参数随机场,导入边坡计算模型中。计算得到的各随机场边坡安全系数和其均值,与为土抗剪强度为常量时边坡安全系数对比,如表1、图4所示。

表1 随机场条件下地震作用下边坡的安全系数

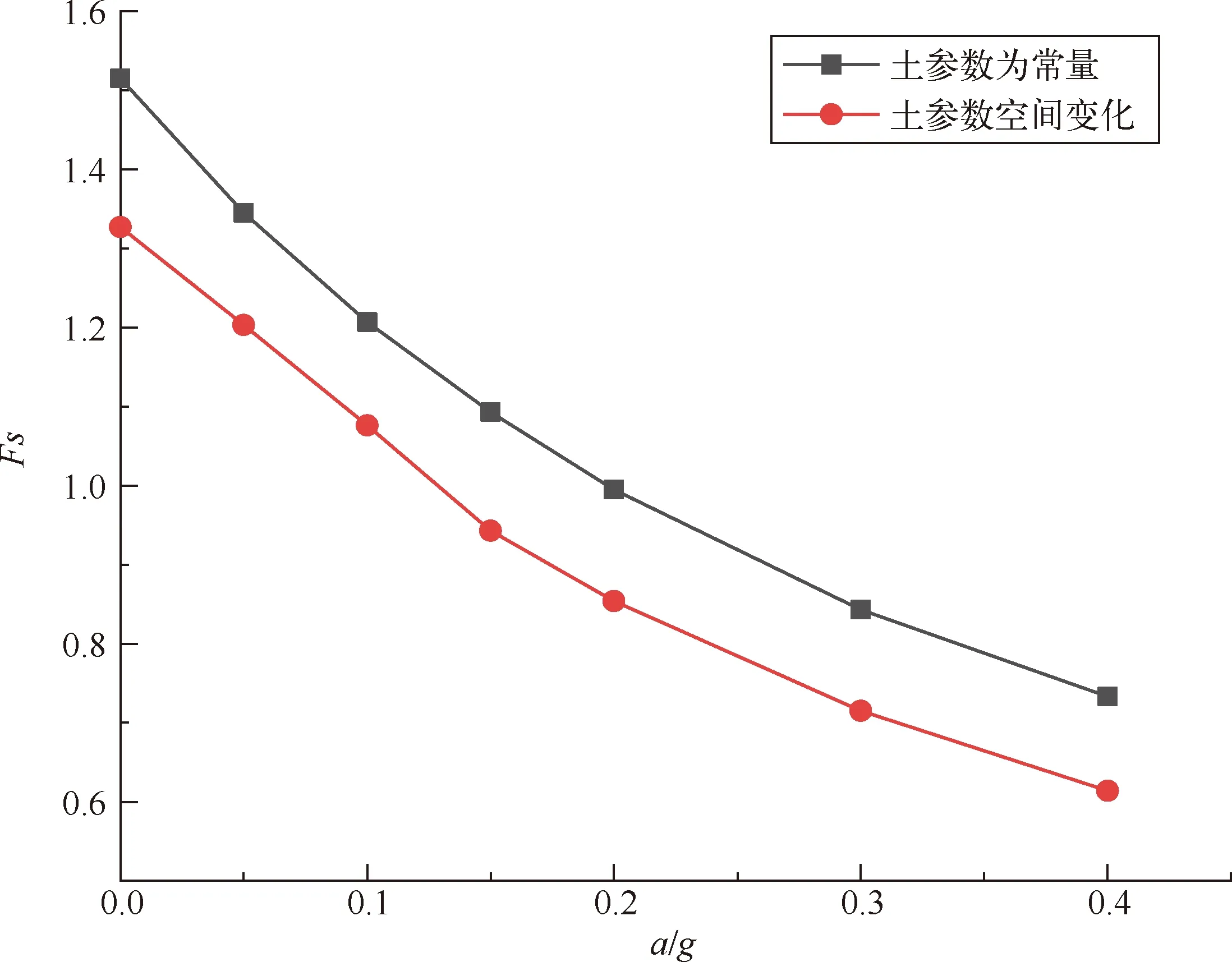
图4 地震作用下边坡的安全系数

由表1和图4可知,在土参数随机变化时安全系数均值,在各种地震作用下都明显低于确定性条件下的安全系数。这是由于考虑了土壤空间变异性这一特点,使得安全系数降低。

在依据得到的各滑动面的滑移体积进行k-means聚类分析时,首先采用手肘法确定[20]最优的k值。对应某个k值,误差平方和SSE(sum of the squared errors)为

(6)

其中,xj为属于j类的所有数据点。

为了确定最优k值,对各簇内的数据进行了误差分析结果如图5所示。图5表明,误差平方和SSE的拐点出现在k=4,故此组数据的最优聚类数量为4。

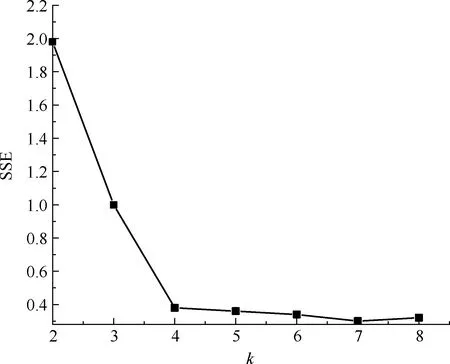
图5 SSE随k值变化(a=0.05g)

对于这个算例,分别采用边坡的最不利单一滑动面、多滑动面传统方法和代表性滑动面计算的边坡系统失效概率,结果如表2和图6所示。

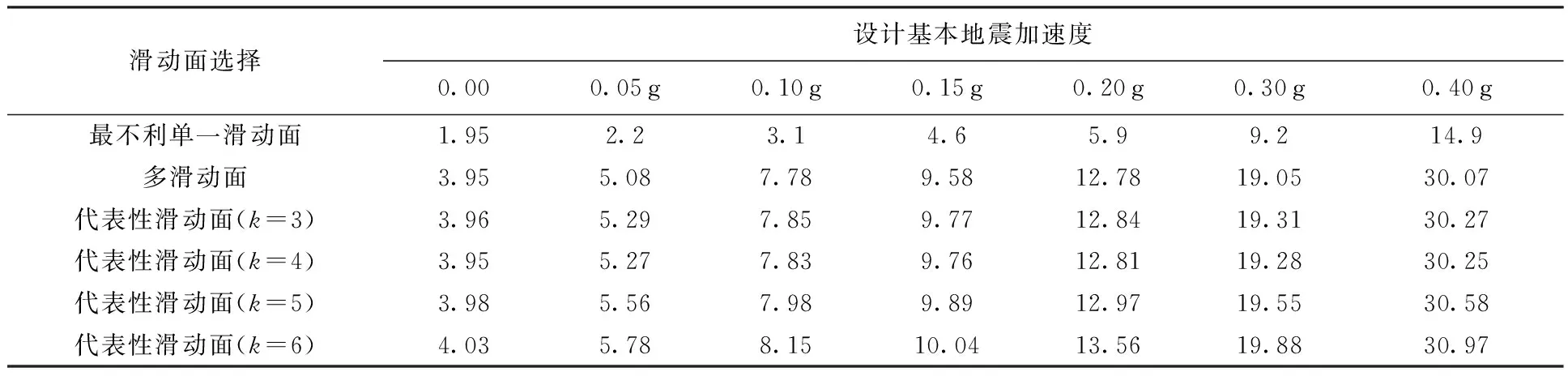
表2 地震作用下边坡的失效概率Pf(%)

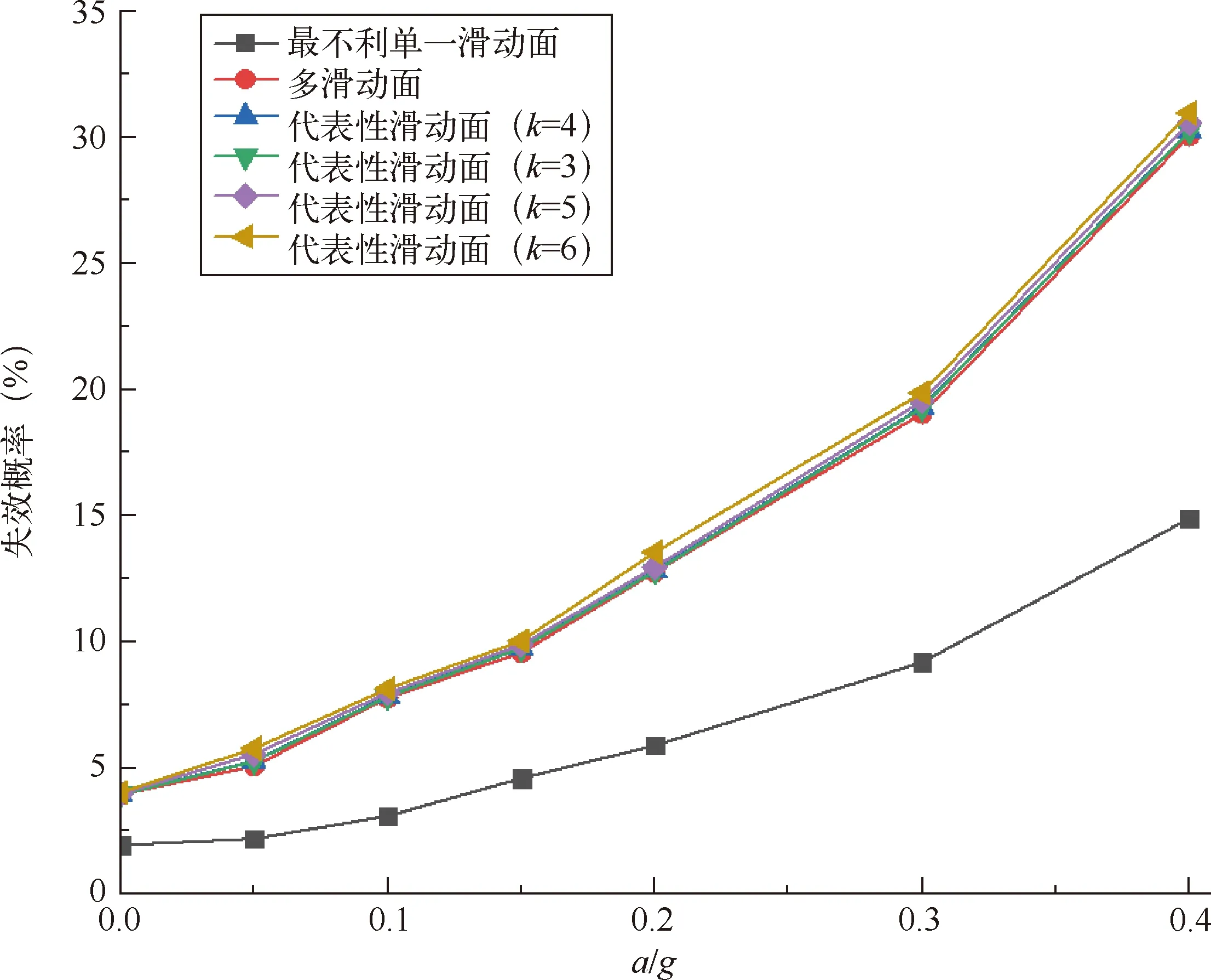
图6 地震作用下边坡的失效概率Pf(%)

如表2和图6结果所示,随着地震水平加速度的增加,边坡的系统失效概率呈非线性增加。在各种地震作用下,最不利单一滑动面的失效概率均小于相应的系统失效概率,约是系统失效概率的50%,这表明根据最不利单一滑动面确定的失效概率明显高估了边坡的安全,这表明分析边坡系统失效概率的必要性。

表2和图6结果显示,代表性滑动面所得系统失效概率略高于传统方法计算结果,偏于安全,其中当聚类数为最优值k=4时,最大误差为6.1%。但是,代表性滑动面确定失效概率的计算量明显降低,本算例中代表性滑动面个数为4,而按传统方法需要计算96个滑动面,计算量为传统方法计算量的1/24。

3 结论

(1) 随着地震水平加速度的增加,边坡的系统失效概率呈非线性增加。由最不利单一滑动面计算的失效概率约是系统失效概率的50%,以最不利单一滑动面的失效概率表示边坡的失效概率会明显高估边坡整体的安全,这表明计算系统失效概率的必要性。

(2) 采用代表性滑动计算地震作用下边坡系统可靠度方法,失效概率略高于考虑所有潜在滑动面的传统方法所得结果。虽然计算精度略有降低,但高估失效概率偏于安全。相较于传统方法,代表性滑动面计算边坡系统可靠度的计算量比传统方法显著降低。